基于线性约束最小方差的稳健波束形成算法

吕岩，曹菲

(1.火箭军工程大学 核工程学院，西安 710025；2.中国人民解放军96746 部队，库尔勒 841000)

阵列信号处理作为一种空间滤波技术，可通过调整阵元权值控制波束形成，使其高增益主瓣波束指向期望信号(signal of interest, SOI)，同时将干扰信号方向的增益置零，与波达方向估计[1](direction of arrival, DOA)配合达到接收SOI 和抑制干扰的目的[2]。目前，波束形成已被广泛应用于雷达、声呐、地震波监测、现代通讯和医学成像等诸多领域[3-5]。

波束形成效果与DOA 的估计精度密不可分，因此，当DOA 估计出现偏差时，波束形成算法性能会严重下降[6-7]。对此，国内外学者开展了大量的研究工作，提出了许多稳健波束形成的算法，主要包含线性约束最小方差[8](linearly constrained minimum variance, LCMV)算法、对角加载算法[9]和最差性能优化波束形成算法[10]等。其中对角加载算法通过设置惩罚权值作为加载因子，有效提高了波束形成的稳健性，但加载因子的选取目前并不存在严格的标准，使算法的应用受到限制。最差性能优化算法通过求解优化问题确定加载因子大小，与对角加载算法相比具备一定优势，但在信噪比[11](signal noise ratio, SNR)较高时，性能会有明显的下降。广义旁瓣相消(generalized sidelobe canceller, GSC)算法是LCMV 的一种等效实现算法[12-13]，能够将LCMV 转变为无约束优化问题，GSC 模型分为两支路，其中主支路允许期望信号通过，辅助支路允许干扰信号和噪声通过，并利用两支路所含信号的差异进行自适应相消。

本文基于LCMV 算法，分别以平面阵列天线和均匀线阵为对象，针对平面阵俯仰角DOA 估计偏差，采用在SOI 方向附近增加线性约束的算法提高波束形成稳健性；而后，针对文献[7]以损失算法自由度为代价的不足，通过添加阻塞矩阵预选环节改进了GSC 模型，避免了在SOI 方向附近添加线性约束，因此，所提算法可在提升波束形成稳健性的同时使其保持原有的自由度。

1 信号模型

1.1 均匀线阵

假设 W个具有任意方向性的阵元沿直线均匀排列，间距为窄带入射信号半波长。对于 K个远场入射信号，则第i个阵元的输出为

1.2 矩形平面阵

平面阵列是线性阵列的一种推广，假设 M行N 列的均匀矩形平面阵列，阵元总数为 Q=MN，如图1 所示。

图1 平面阵列Fig.1 Planar array

2 波束形成算法

2.1 LCMV 算法

LCMV 算法通过最小化输出功率，同时满足若干线性约束条件，从而确定阵元的权值矢量，问题的表达式为

2.2 GSC 算法

如图2 所示，GSC 算法的权值矢量分为 wq和wa两部分，分别代表主支路权向量和辅助支路权向量。

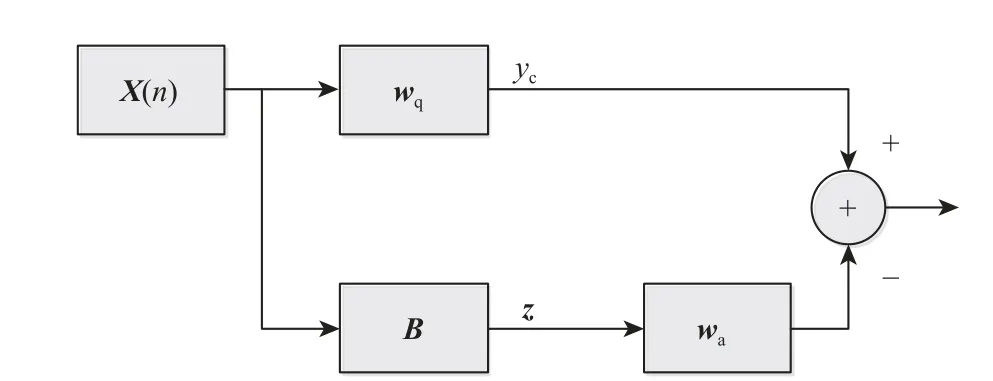
图2 GSC 模型Fig.2 Model of GSC

图2 中阻塞矩阵 B 为 Q×(Q-J-1)维，起阻塞SOI 的作用，满足 BHC=0。GSC 的权向量可表示为

式中：

2.3 平面阵稳健波束形成算法和改进GSC 模型

2.3.1 平面阵稳健波束形成算法

假定 (θs,φs)为平面阵列SOI 的DOA 估计值，此时为保证SOI 损失最小，设置 C=[a(θs,φs)]和约束向量 f =1，可得

采用式(17)作为约束矩阵相当于在期望方向附近添加了一组“字典”，真实DOA 可利用该字典进行稳健匹配，示意如图3 所示。

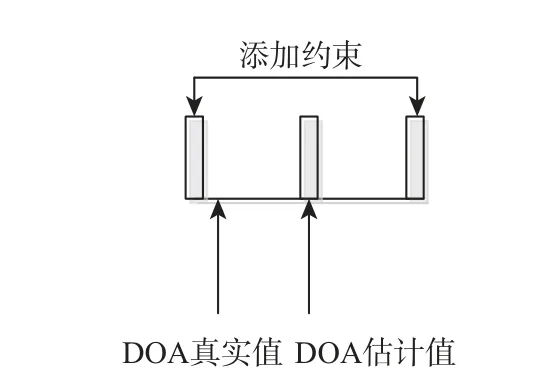
图3 字典示意图Fig.3 Sign for dictionary

采用 f 为全1 向量进行约束会产生过约束现象，导致波束形成产生畸变，取：

式中：λ1,λ2,···,λk为拉格朗日乘子，令式(20)导数为0 并求解，可得

2.3.2 改进GSC 模型

文献[7]通过添加线性约束的方式提高了LCMV 算法的稳健程度，但以消耗算法自由度为代价，且仅利用了GSC 算法的主支路权向量，未充分利用辅助支路。GSC 算法主支路和辅助支路的主要区别在于是否含有SOI，理想情况下主支路中SOI 含量较高，辅助支路不含SOI，所以两支路信号的相关程度代表着阻塞矩阵的阻塞效果。当主支路和辅助支路相关程度较高时，表示阻塞矩阵效果降低，DOA 的真实值和估计值之间存在误差；反之，相关程度较低时，表示阻塞效果较好，基于该项性质，本文在GSC 模型中添加阻塞矩阵预选环节，如图4 所示。

根据图4，在SOI 方向附近选取不同角度计算阻塞矩阵，利用不同阻塞矩阵计算两支路 yc和 z的互相关向量，并计算互相关向量的 l1范数，选择较小范数时的阻塞矩阵作为最佳矩阵。所提算法即为对阻塞矩阵进行预选择，未在SOI 的DOA 附近添加额外约束，因此未对算法自由度产生影响，改进GSC 算法的流程如下：

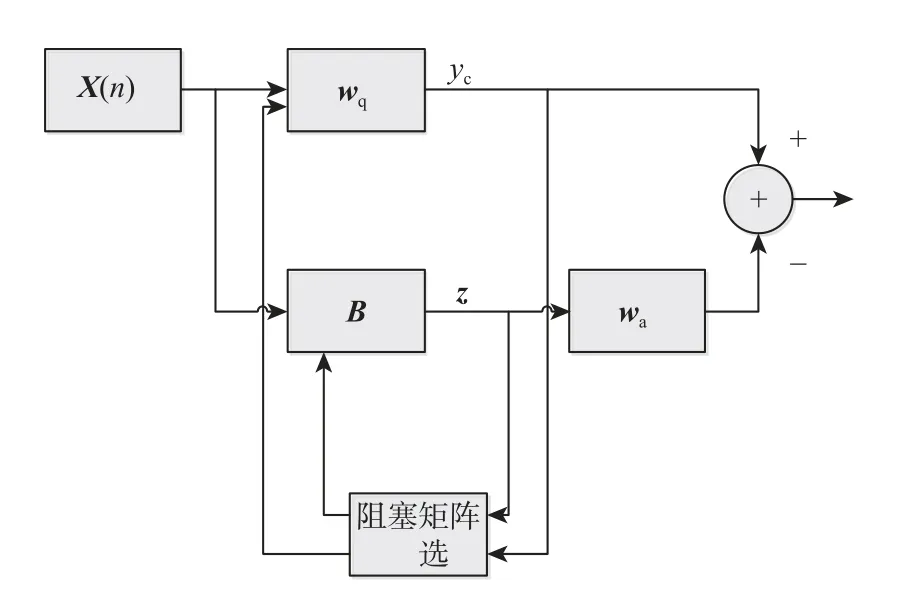
图4 改进GSC 模型Fig.4 Model of improved GSC

步骤 1 选取SOI 的DOA 附近角度计算阻塞矩阵。

步骤 3 计算 yc和 z的互相关向量，并计算相关向量的 l1范数。

步骤 3 执行 ζ次步骤2，选择最小 l1范数时的阻塞矩阵作为 Bbest。

步骤 4 利用 Bbest计 算权值 w。

可知，改进GSC 算法和原算法的主要差别在于矩阵预选部分，经算法复杂度分析可得

式中：W 和 ζ分别为天线阵元数量和预选阻塞矩阵次数。

3 仿真分析

3.1 平面阵稳健波束形成算法仿真

仿真基于8×8 的矩形平面阵，为便于比较俯仰角出现DOA 失配时对波束形成性能的影响，先将方位角设定为统一值，设置SOI 的DOA 为(θs,φs)=(15°,10°)，2 个干扰的DOA 分别为 (15°,-40°)和 (15°,25°)，信噪比为0 dB，干噪比(interference to noise ratio, INR)为10 dB。

图5～图7 分别为采用LCMV 算法生成的空间增益三维图、等高线图和方位角等于15o时俯仰角与波束增益的截面图，可知SOI 方向波束增益为峰值，2 个干扰均被有效抑制。

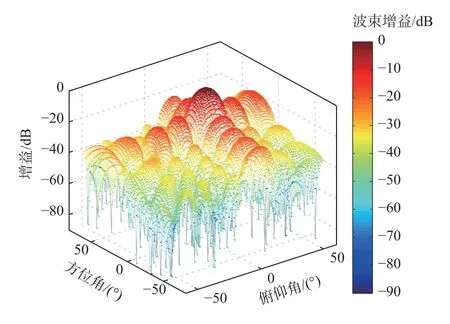
图5 波束增益Fig.5 Pattern synthesis

图6 等高线Fig.6 Contour plot

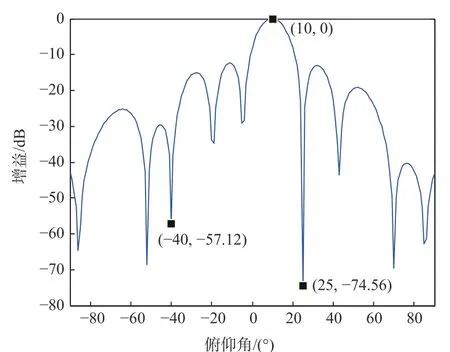
图7 方位角15o 波束截面Fig.7 Sectional drawing of 15o

假设SOI 方向出现DOA 失配，实际俯仰方向波达角为11o，此时俯仰角和增益的截面图如图8所示。可知DOA 失配时，波束图出现较大畸变，无法在SOI 方向形成高增益波束，干扰抑制能力也随之变差，算法性能严重下降。

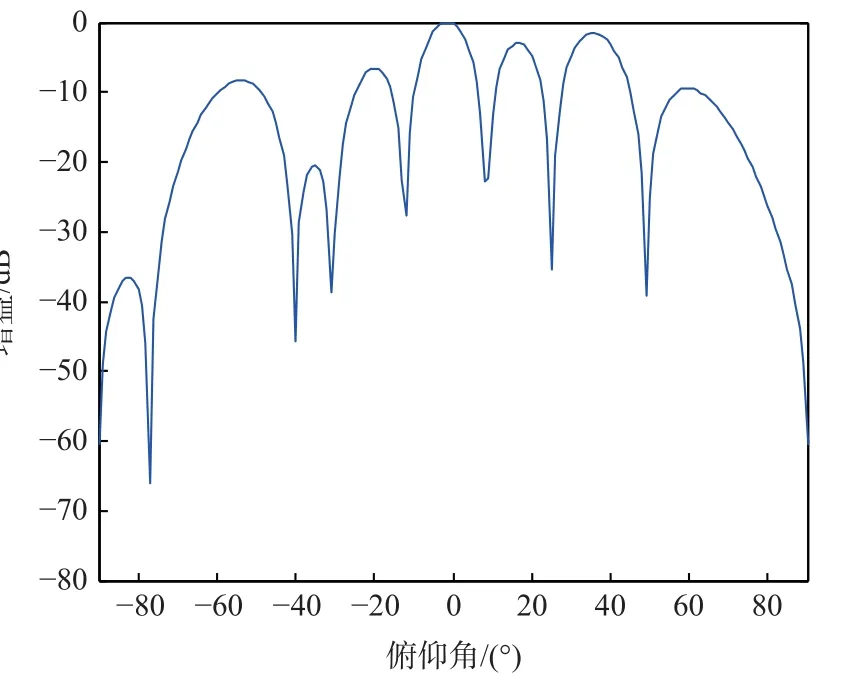
图8 波束畸变Fig.8 Pattern synthesis distortion

设置角度增量 δφ=1°，在SOI 方向附近额外添加2 个约束，则可得

此时俯仰角和波束增益的截面图如图9 所示，可知SOI 方向波束未发生畸变，虽然对2 个干扰的抑制能力略有下降，但仍能达到良好的抑制效果。

图9 DOA 失配增益Fig.9 Pattern synthesis of DOA mismatch

为进一步验证所提算法的性能，将方位角设置为不同数值，SOI 的DOA 设置为 (θs,φs)=(15°,10°)，2 个干扰信号的DOA 分别设置为 (10°,-40°)和 (20°,25°)，实际波达角仍为( θs,φs)=(15°,11°)，此时阵列的空间增益和等高线如图10 和图11 所示。

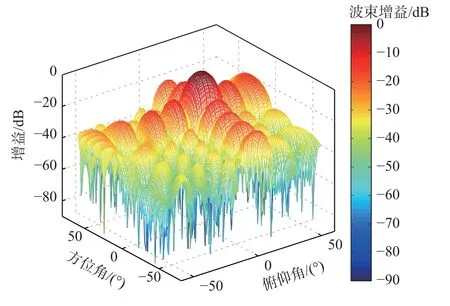
图10 平面阵波束增益Fig.10 Pattern synthesis of planar array

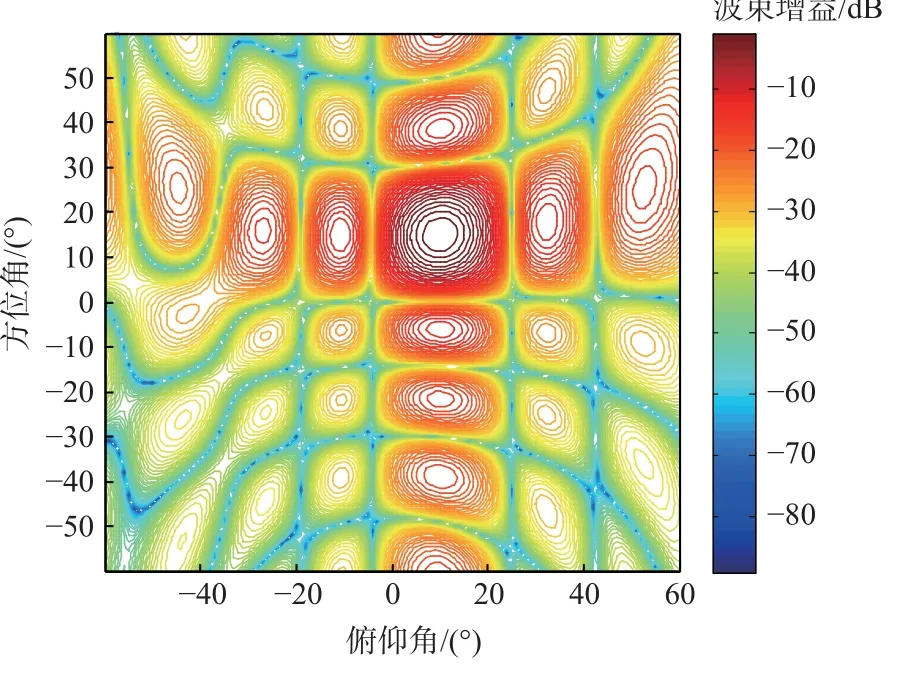
图11 平面阵等高线Fig.11 Contour plot of planar array

为进一步表明测试结果，分别生成方位角为15o、10o和20o时的俯仰角与波束增益的截面如图12 所示。根据图12 可知，主瓣波束未发生畸变，干扰抑制效果良好，添加约束取得了提升波束形成稳健性的作用。

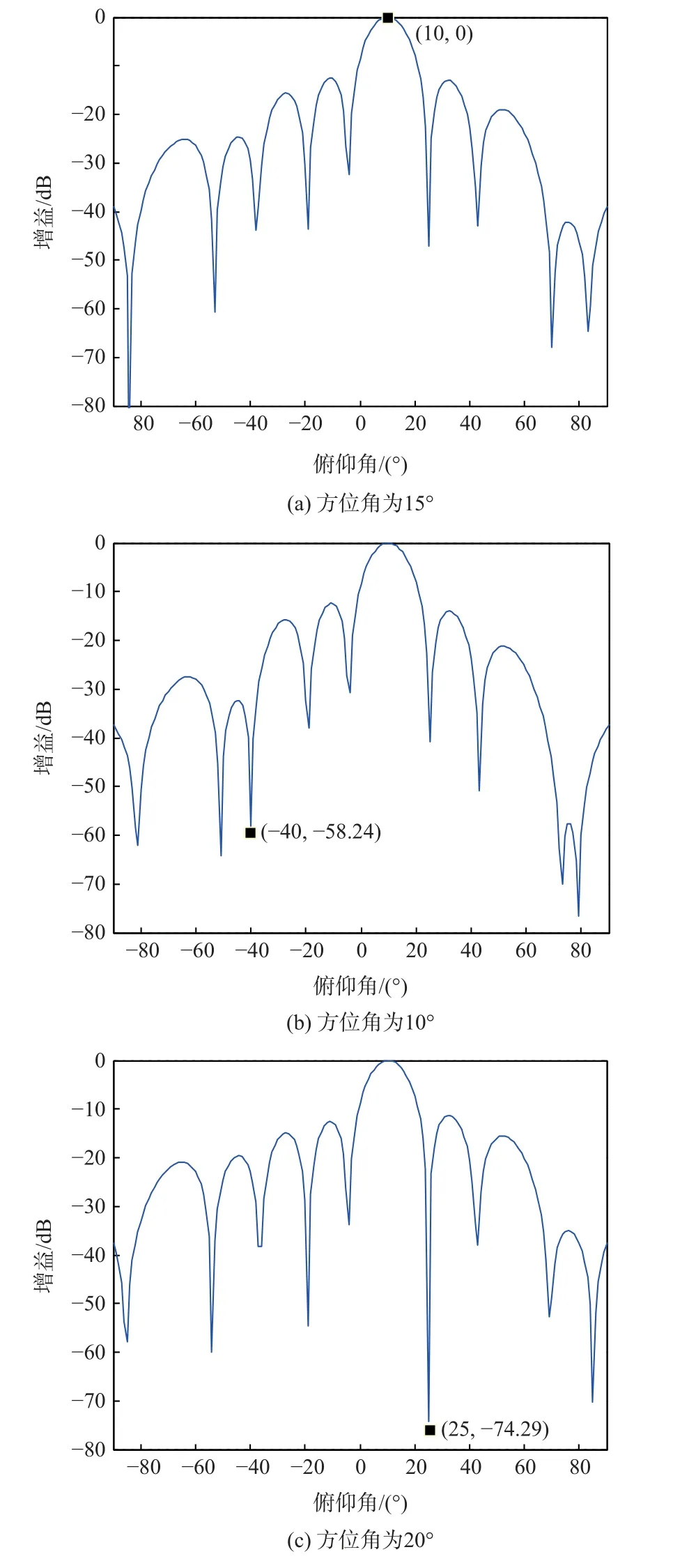
图12 不同方位角的波束截面Fig.12 Sectional drawings of pattern syntheses for different azimuths

3.2 改进GSC 模型仿真

仿真基于16 阵元的均匀线阵，设置SOI 的DOA 为30o，3 个干扰DOA 分别为40o、-25o和-60o，INR 为30 dB。假设信号实际的DOA 为31o，为验证改进GSC 模型的有效性，分别选取29o、30o、31o这3 个DOA 生成阻塞矩阵，并计算 yc和 z互相关向量的 l1范 数，图13(a)为 l1范数随SNR 从-20～20 dB之间的变化趋势（已归一化），图13(a)中蓝、绿和红色曲线分别对应31o、30o和29o。进一步令INR 与随机数rand 相乘，即INR 处于0～30 dB 之间随机变化。图13(b)为该状态下200 次蒙特卡罗[14-15]实验的 l1范数平均值随SNR 的变化趋势，可知蓝色曲线的l1范数最小，说明其更接近真实DOA，应选择31o进行后续计算。

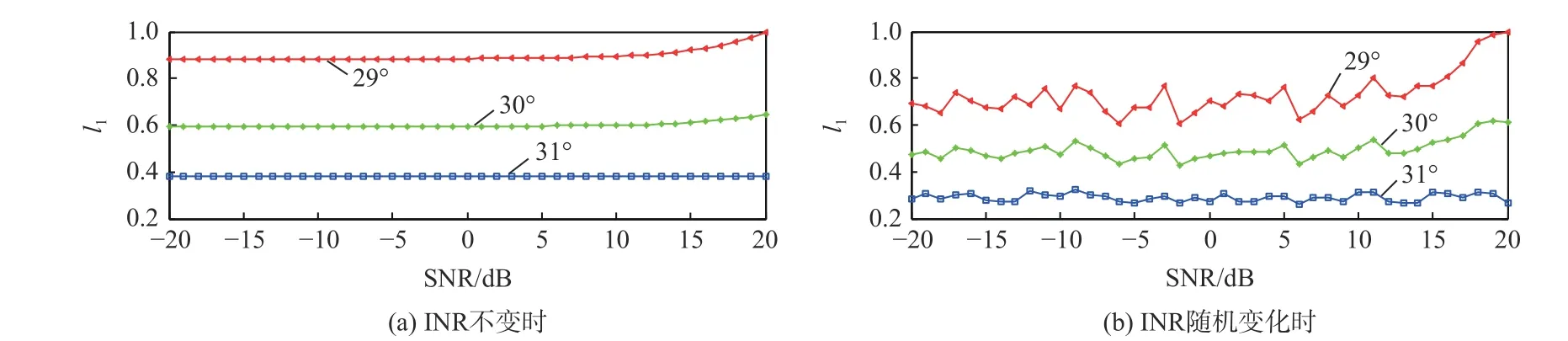
图13 范数变化趋势Fig.13 Trends of norms

选定DOA 为31o构造阻塞矩阵，并求取权值w，图14 为SNR 分别为-10 dB 和10 dB 时，改进GSC模型和文献[7]算法的波束形成对比，从图14 可知2 种算法对-25o方向干扰的抑制能力相近，但改进GSC 模型在40o和-60o方向上的增益要比文献[7]更低，干扰抑制效果更优。

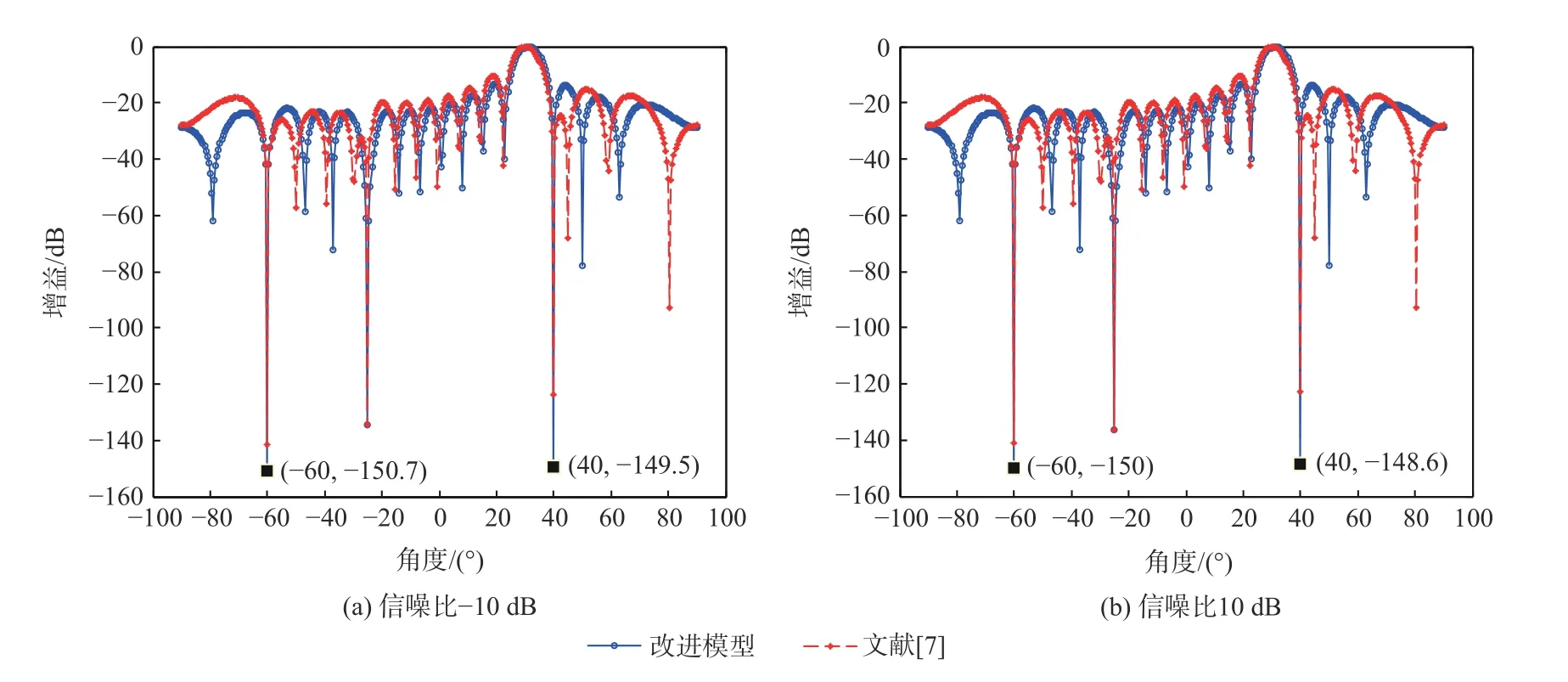
图14 改进GSC 和文献[7]波束形成对比Fig.14 Comparison of pattern synthesis between improved GSC and Ref.[7]

图15(a)为干扰方向不变(40o、-25o和-60o)，SOI的实际DOA 不同时，l1范数随SNR 从-20～20 dB之间的变化趋势（已归一化的200 次蒙特卡罗实验平均值）。图15(b)为实际DOA 不变，干扰信号方向不同时，l1范数随SNR 从-20～20 dB 之间的变化趋势。从图15 中可以看出，与实际DOA 偏差越大，则 l1范 数越大，表示 yc和 z之间的相关程度较高，阻塞矩阵对于SOI 的阻塞效果不理想。随着与实际DOA 偏差的逐渐降低，yc和 z之间的相关程度降低，阻塞矩阵对于SOI 的阻塞效果逐步提升。

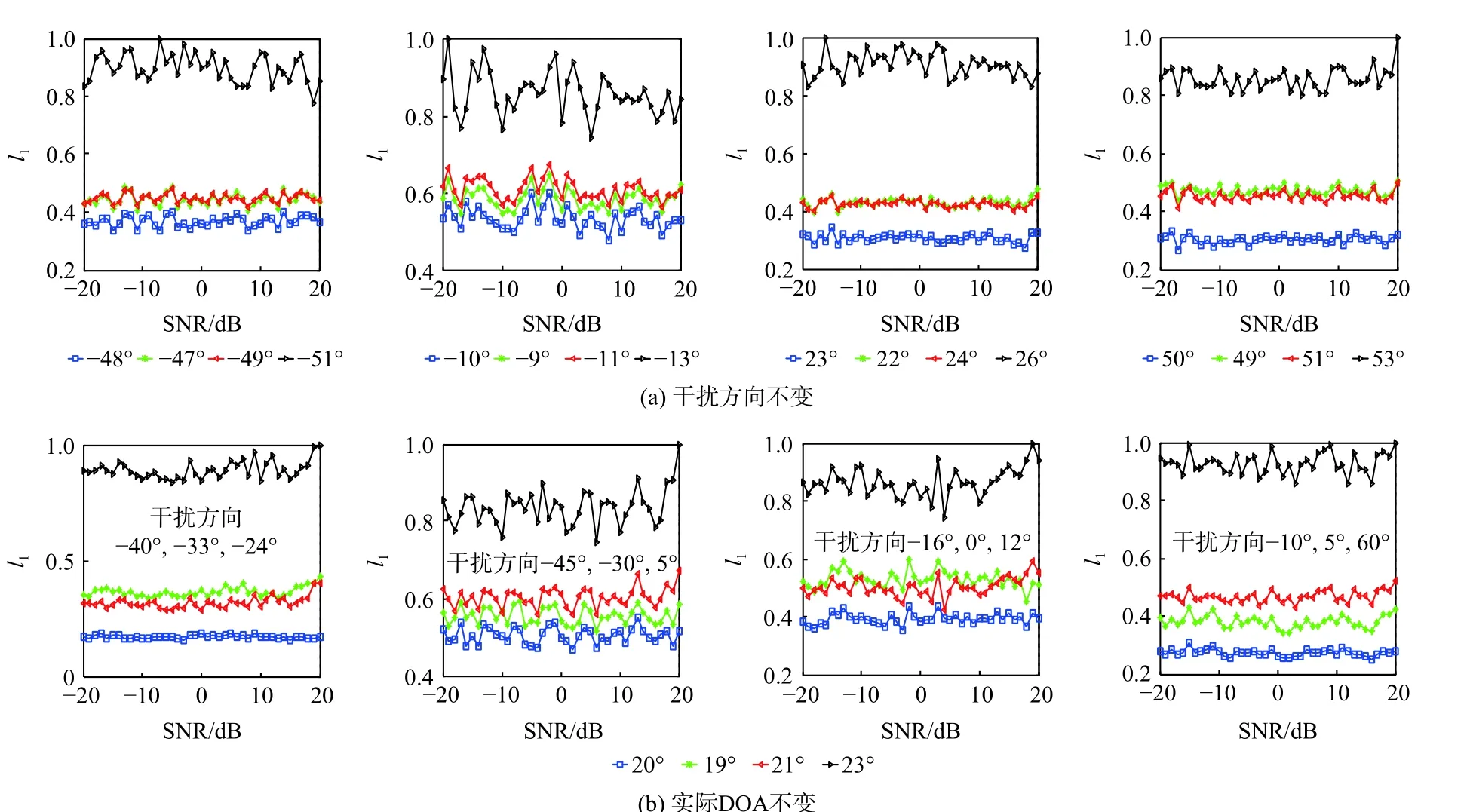
图15 不同参数时的范数变化趋势Fig.15 Trends of norms under different parameters

表1 和图16 为GSC、文献[7]和改进GSC 算法运行耗时的对比，仿真平台为MATLAB2014，CPU3.40 GHz、RAM16 GB。根据结果可知当阵元数量较少时，3 种算法运行耗时相差不大。随着阵元数量增多，3 种算法的运行时间逐渐增加，其中改进GSC 算法增加的最快，当阵元数量为100 时，改进GSC 算法约比文献[7]算法耗时多2.4 倍。

表1 不同阵元数量耗时Table 1 Time consumed versus different elements

4 结 论

1）本文针对平面阵列天线波束形成过程中的DOA 估计失配问题，以俯仰角存在误差为例，采用在参考方向附近生成“字典”，增加线性约束的算法，起到增强波束形成稳健性的作用。

2）针对增加线性约束会导致算法自由度降低的问题，采用增加阻塞矩阵预选环节改进了GSC算法，通过 l1范数平均值变化趋势、波束形成增益和算法运行时间三方面的对比，验证了改进GSC 算法虽然会增加运行时间，但可以在干扰方向产生更深的零陷，并可使算法保持原有自由度；

下一步将研究平面阵俯仰、方位角双失配时的线性约束添加算法和将改进GSC 算法应用于平面阵。