基于修正似然滤波的无人机编队相对导航方法

苏炳志，王磊，张红伟，汪海涵，石璐璐

(1.中国直升机设计研究所，天津 300300；2.陆军装备部驻天津地区航空军代室，天津 300384)

无人机采用编队形式开展协同侦查、联合攻击和战场毁伤评估等任务，可以有效提高作战效率，是未来体系化作战的主要模式[1]。高精度、高可靠的相对导航系统是无人机编队协同完成既定任务的关键技术。基于INS/GPS 的相对导航方式是初期最常用的一种导航机制，然而从外界接收到的GPS 信号存在极易受到故意干扰和电子欺骗的缺陷[2-3]。因此，学者们研究了一种不依赖于外部传感器的相对导航系统-视觉辅助惯性的相对导航[4]。基于INS/Vision 的相对导航精度很大程度上取决于视觉传感器和惯性传感器数据融合方法。

由于形式简单和易于实现，扩展卡尔曼滤波(extended Kalman filtering, EKF)是相对导航滤波器中最常用的一种滤波算法[5]。由于只利用一阶泰勒级数对非线性系统进行线性化，EKF 在强非线性系统中表现出不令人满意的性能甚至使滤波器发散[6]。学者们使用采样方法近似非线性分布解决非线性问题的思维，提出一系列确定性采样非线性高斯滤波。文献[7-8]从直观的统计信息转换视角开发了基于无迹变换的卡尔曼滤波(unscented Kalman filtering, UKF)。然而，在处理高维系统时，UKF 中存在负权重的Sigma 点，致使状态估计协方差出现非正定，这将影响滤波器的稳定性。Arasaratnam等将笛卡儿坐标系下的积分转换成球面和径向积分推导了基于三阶球面-径向容积准则的容积卡尔曼滤波(cubature Kalman filtering, CKF)[9-10]。与UKF不同，CKF 的权重全为正值，因此，其具有更好的数值稳定性。

文献[5-10]中各种滤波算法都是基于量测是实时可用的假设开发得到的。但实际上，由于通讯或网络堵塞等因素的存在，到达滤波数据处理中心的量测数据往往存在随机时延[11]。为了处理量测随机时延问题，学者们基于向后逆推和向前正推导提出了无序Sigma 点卡尔曼滤波[12]和乱序粒子滤波[13]。尽管这些滤波算法能够很好地处理随机延迟量测，但需要时间戳来计算延迟时间，并且只能处理延迟时间不变的量测数据。为了摆脱这种限制和克服不足，学者们从延迟概率的角度出发，利用伯努利随机变量建立实际接收量测与理想量测之间的关系，对随机时延系统重新建模，提出了多种滤波体制以解决量测数据具有一步或多步延迟问题。Hermoso-Carazo 和Linares-Perez[14-15]针对一步随机延迟量测提出改进型的EKF 和UKF，通过对状态和量测噪声的扩增，将其推广到多步随机时延系统中。Wang 等[16]概括性地推导了具有一般普遍性的单步随机时延非线性高斯滤波算法，并给出了单步随机时延容积卡尔曼滤波(one-step randomly delayed CKF, ORD-CKF)算法的详细过程。张勇刚等[17]提出一种带多步随机延迟量测高斯滤波器的一般框架，并给出多步随机时延容积卡尔曼滤波(multiplestep randomly delayed CKF, MRD-CKF)算法的具体计算流程。Esmzad 和Esfanjani[18-19]通过修正常规卡尔曼滤波的似然函数，提出一种能够处理多步随机时延的修正似然卡尔曼滤波，该算法利用量测残差调节权重因子，使得滤波算法具有更高的估计精度；之后将其推广到非线性高斯系统中。

在文献[18-19]的研究基础上，采用估计精度和稳定性较好的三阶球面-径向容积准则计算非线性系统中的高斯加权积分，提出一种修正似然容积卡尔曼滤波(modified likelihood CKF, ML-CKF)算法，解决无人机编队相对导航系统中视觉量测存在多步随机时延问题。所提算法的递归过程包括状态预测和量测更新2 个步骤。状态预测是基于三阶球面-径向容积准则和多步随机时延系统得到的。由于存在时延，接收到的量测与系统过去状态相关，在量测更新中通过边缘化延迟变量来计算滤波的似然函数以从延迟量测中准确地提取信息。建立无人机编队相对导航系统模型；采用一种无约束的三参数罗德里格斯参数表示姿态误差来传播和更新姿态四元数，设计基于ML-CKF 的相对导航滤波器。最后，开展仿真验证，对比了本文所提算法ML-CKF 与CKF、ORD-CKF 和MRD-CKF 的性能。

1 修正似然容积卡尔曼滤波

1.1 问题阐述及预处理

考虑式(1)所示的离散系统：

式中：yk为实际接收到的量测量；τ0=1，τs(1 ≤s ≤d)为相互独立的伯努利随机变量，τ(s,j)为

式中：τ(s,j)(s=0,1,···,d)中只有一个系数取1，其他均为0；这意味着每个时刻接收到的实际量测 yk是当前时刻或者过去时刻量测量 zk-s(s=0,1,···,d)中的一个。

量测延迟 s(0 ≤s ≤d)步的概率为

式中：pj为伯努利随机变量 τj(0 ≤j ≤d)的期望，即τj取1 的概率。

1.2 修正似然非线性高斯滤波框架

由式(2)可知滤波器实际接收到的量测 yk是{zk-s}ds=0中 的 一个，即 yk的 值与 xk,xk-1,···,xk-d相关。因此，需要将 xk-1,xk-2,···,xk-d扩增到当前状态当中，得到扩增状态：

不同于常规贝叶斯滤波中的单峰概率密度函数，式(9)似然函数是一多峰概率密度函数。由于式(9)包含更多关于量测与状态之间的信息，因此，与单峰概率密度函数相比，式(9)所表示的似然函数更加精确。在量测噪声服从高斯分布时，似然函数式(9)可以写成混合高斯形式：

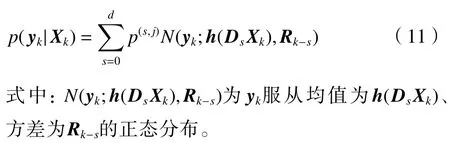
1.2.2 传播预测分布

假设先验分布 p(Xk-1|y1:k-1)和状态传递分布p(Xk|Xk-1)均为高斯分布，根据Chapman-Kolmogorov方程，可得预测分布：

1.2.3 更新后验分布

将式(11)和式(12)代入式(8)，可得到后验分布：

1.3 修正似然容积卡尔曼滤波算法

采用三阶球面-径向容积准则计算修正似然非线性高斯滤波中的高斯加权积分，详细给出修正似然容积卡尔曼滤波算法的递推计算更新过程。

1.3.1 状态预测

根据式(5)，可得k -1时 刻的扩增状态估计Xˆk-1/k-1及其协方差 Pk-1/k-1：

修正似然容积卡尔曼滤波算法的具体流程如图1 所示。

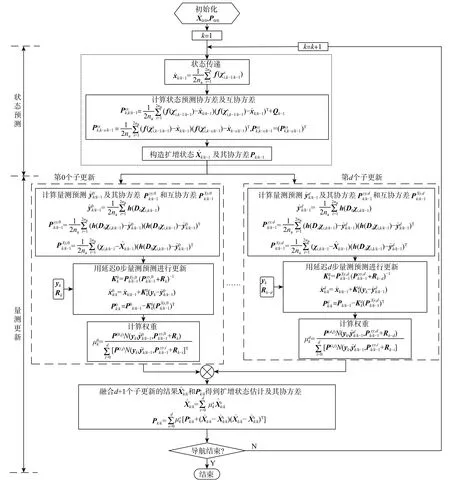
图1 修正似然容积卡尔曼滤波流程Fig.1 Flowchart of modified likelihood cubature Kalman filtering

2 相对导航系统建模

以僚机本体系为基准建立僚机和长机之间的相对姿态、位置和速度方程，以长机上的导航相机与僚机上特征光点之间的视线矢量作为量测量，将长机上的惯性和视觉量测信息传输给僚机进行融合估计得到僚机和长机之间的相对运动信息。

2.1 相对导航方程

2.1.1 相对姿态运动方程

采用工程实用性强的四元数表示姿态，即

2.2 相对导航传感器测量模型

2.2.1 惯性导航系统测量模型

加速度计和陀螺仪是惯性导航系统中重要的传感器，其测量模型分别为

3 相对导航滤波器设计

3.1 状态向量

若直接把受归一化约束的四元数作为状态分量，存在四元数姿态协方差阵奇异性问题，因此，采用一种无约束的三参数罗德里格斯参数表示姿态误差来传播和更新姿态四元数，进行滤波器设计。

定义状态矢量：

2.2.2 视觉导航系统测量模型

视觉导航系统的量测量是长机上导航相机与僚机上特征光点之间的视线矢量，其测量原理如图2

3.2 状态预测

k-1时刻相对导航滤波器的扩增状态为

将式(64)～式(66)和式(23)～式(26)代入式(20)中可得到扩增状态预测及其协方差。

3.3 量测更新

融合式(19)～式(36)修正似然容积卡尔曼滤波算法和式(52)～式(71)相对导航滤波器设计过程，基于ML-CKF 的相对导航滤波器流程如下。

1) 状态预测。

① 根据式(21)计算状态预测容积点；

② 根据式(54)～式(57)计算姿态四元数误差；

③ 根据式(58)和式(59)计算状态预测所需的姿态四元数容积点；

④ 根据式(60)、式(65)和式(66)进行相对姿态、相对位置、相对速度、加速度计漂移和陀螺仪漂移递推；

⑤ 根据式(64)计算经过状态递推后的罗德里格参数估计值；

⑥ 根据式(23)～式(26)和式(20)计算扩增状态及其协方差。

2) 量测更新。

① 根据式(27)计算量测更新所需容积点；

② 根据式(67)计算延迟 s(0 ≤s ≤d)步量测预测容积点；

③ 根据式(28)～式(31)计算延迟 s(0 ≤s ≤d)步量测预测均值、协方差、互协方差和滤波增益；

④ 根据式(32)～式(33)计算第 s个子更新结果；

⑤ 根据式(34)～式(35)进行扩增状态及其协方差更新；

⑥ 根据式(71)计算量测更新后的罗德里格斯参数，根据式(70)可见相对导航位置和速度可从扩增状态中获取。

4 仿真分析

为了验证所提算法在处理随机时延量测上的优越性，将开展数值仿真验证，将ML-CKF 与现有CKF[9]、ORD-CKF[16]和MRD-CKF[17]进行比较。

4.1 仿真初始条件

惯性器件、视觉导航系统的采样时间及滤波步长均为0.1 s，传感器的偏差相关参数如表1 所示。

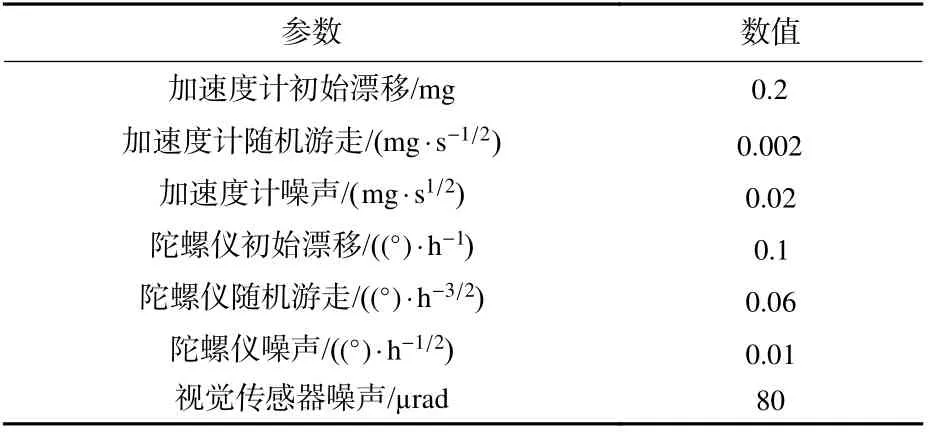
表1 惯性和视觉传感器偏差参数Table 1 Deviation parameter of inertial and visual sensors

3 个特征光点即可保证惯性/视觉相对导航系统完全可观测，为了提高相对导航精度，将特征光点数提高一倍，6 个特征光点位置分布如表2 所示。

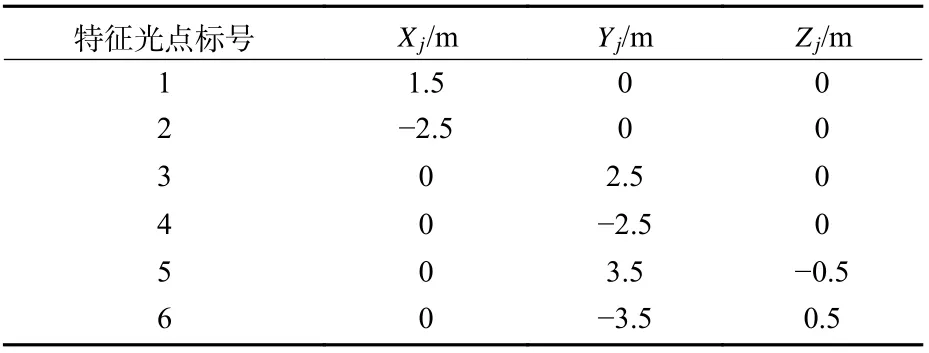
表2 特征光点位置列表Table 2 List of beacon locations

假设长机运动在北-天-东坐标系内，初始时刻从经度 120°、纬度 40°和高度1 000 m 位置开始运动，僚机与长机形成编队飞行，参考文献[20]规划典型轨迹，长机和僚机的位置变化方程如式(72)和式(73)所示，相应的运动轨迹如图3 所示。

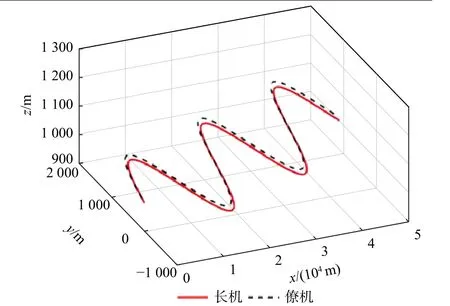
图3 长机和僚机飞行轨迹Fig.3 Flight path of leader and follower

假设视觉量测最大延迟步数为3 步，无延迟概率 p(0,j)、延迟1 步概率 p(1,j)、延迟2 步概率 p(2,j)和延迟3 步概率 p(3,j)分别为

4.2 仿真结果与分析

取延迟概率 pd=0.3进行仿真，得到仿真结果如图4～图9 所示。

图4 相对位置估计误差Fig.4 Estimation error of relative position

图4～图6 分别为ML-CKF 估计得到的相对位置、相对速度和相对姿态误差，从图4～图6 中曲线可知基于ML-CKF 的相对导航误差曲线能够快速收敛。图7～图9 是CKF、ORD-CKF、MRD-CKF和ML-CKF 算法100 次蒙特卡罗打靶仿真三维相对位置、速度、姿态误差模值的比较结果。仿真结果表明，CKF 的估计精度最差，这是由于其未对延迟量测进行处理；MRD-CKF 和ML-CKF 的估计精度高于ORD-CKF，这是因为MRD-CKF 和ML-CKF能够处理量测存在多步随机时延问题，而ORDCKF 只能处理单步随机延迟量测。此外，与MRDCKF 相比，ML-CKF 具有更高的估计精度，这归功于ML-CKF 中的加权因子是在延迟概率的基础上根据残差实时调节的。如表3 所示4 种滤波算法单次计算耗时，从表3 中可见本文所提算法MLCKF 计算耗时低于MRD-CKF，高于CKF 和ORDCKF；但ML-CKF 的估计精度远高于CKF 和ORDCKF；从估计精度和计算耗时综合考虑角度出发，在工程应用中ML-CKF 是一种折中的选择。

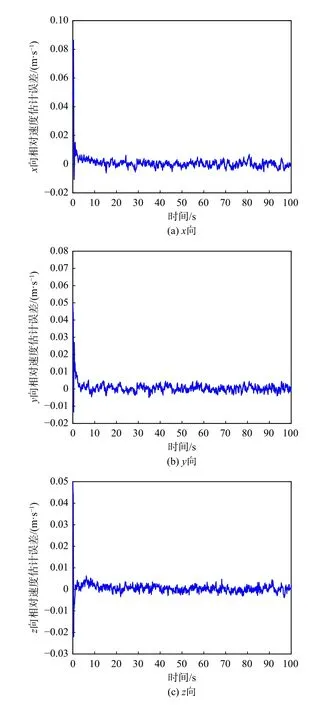
图5 相对速度估计误差Fig.5 Estimation error of relative velocity

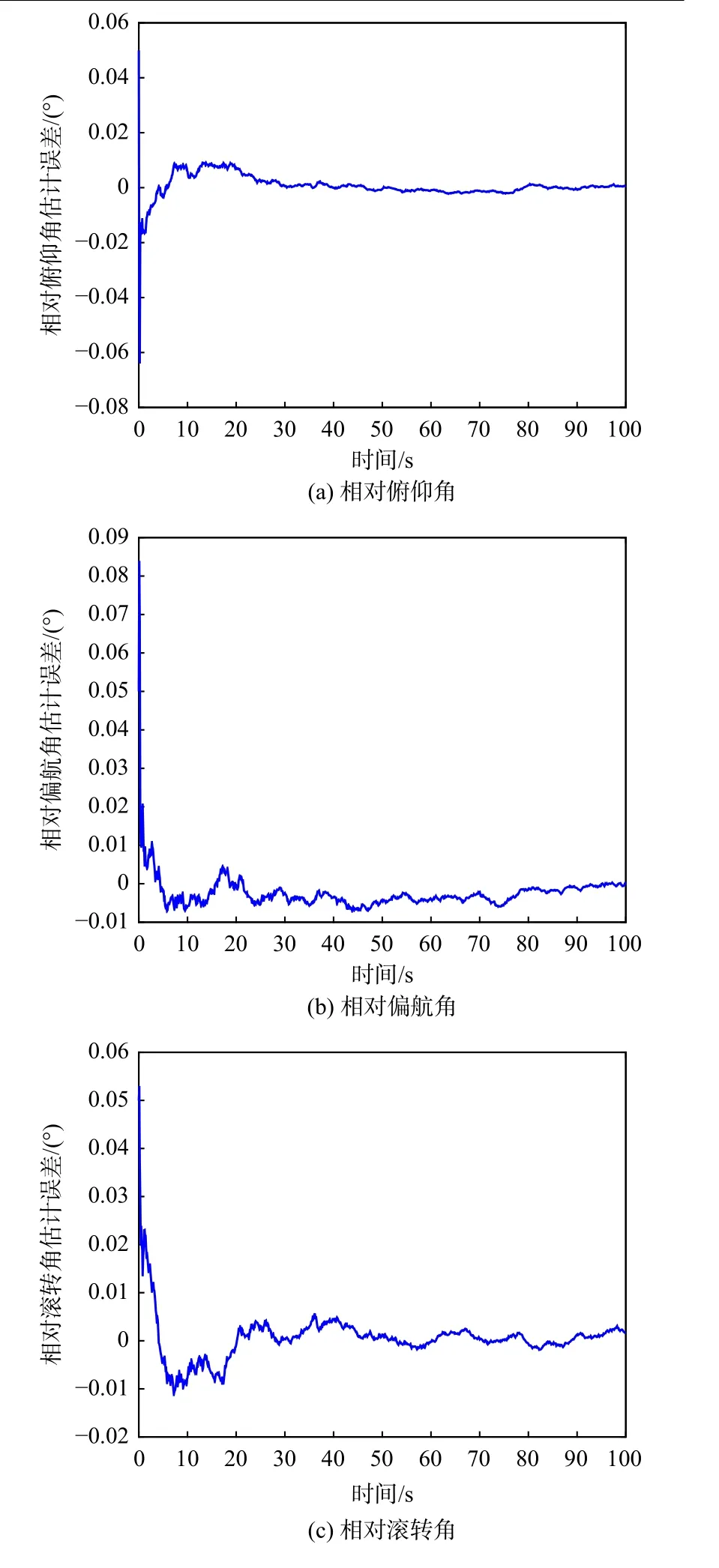
图6 相对姿态估计误差Fig.6 Estimation error of relative attitude

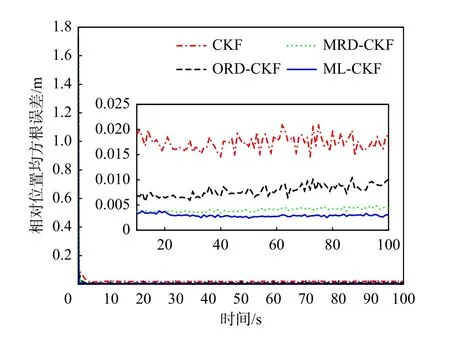
图7 相对位置估计精度对比Fig.7 Comparison of estimation accuracies of relative positions

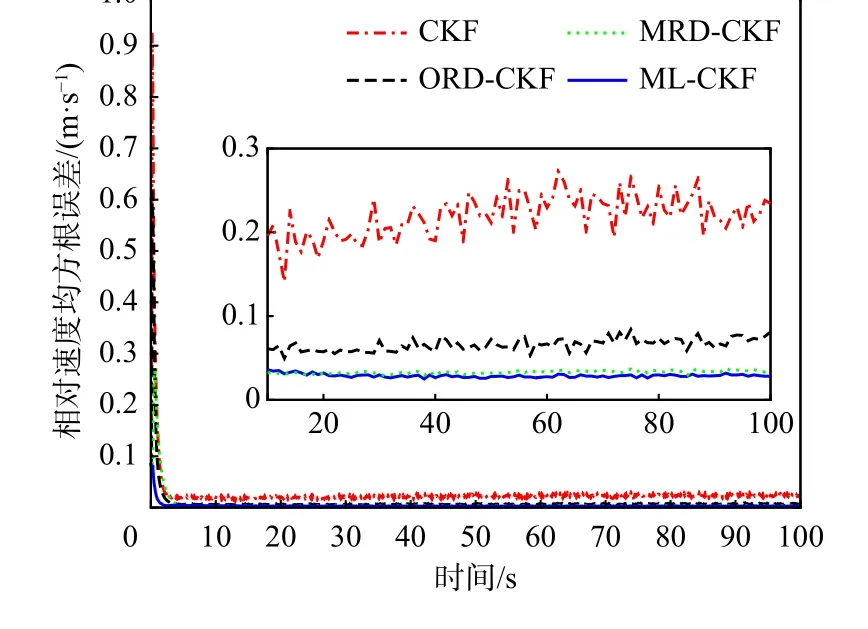
图8 相对速度估计精度对比Fig.8 Comparison of estimation accuracies of relative velocities

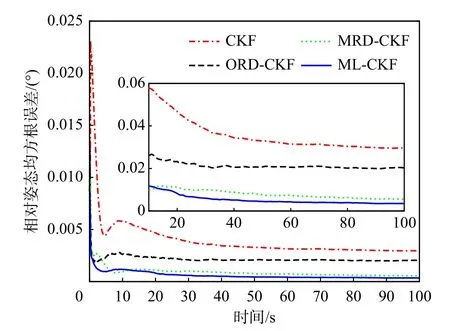
图9 相对姿态估计精度对比Fig.9 Comparison of estimation accuracies of relative attitudes

表3 不同滤波算法的计算耗时Table 3 Single computation time of different filtering algorithms

5 结 论

1) 仿真结果表明，采用无约束三参数罗德里格斯参数表示姿态误差来传播和更新姿态，设计基于修正似然容积卡尔曼滤波的无人机编队，相对导航滤波器在视觉延迟量测存在多步随机延迟的情况下，也能精确估计出相对位置、速度和姿态。

2) 通过蒙特卡罗打靶仿真统计多次仿真试验的均方根误差，基于ML-CKF 的相对导航精度高于CKF、ORD-CKF 和MRD-CKF，验证了所提算法的优越性。

3) 提出的基于ML-CKF 的视觉辅助惯性相对导航算法还可应用于无人机空中加油、卫星编队相对导航和航天器交会对接等航空航天领域。