直反信号协同的GNSS-R BSAR 距离多普勒成像算法

吴世玉，杨东凯，王峰，苗铎

(北京航空航天大学 电子信息工程学院，北京 100191)

基于全球导航卫星系统反射信号的双基地合成孔径雷达(global navigation satellite systemreflectometry bistatic synthetic aperture radar，GNSS-R BSAR)以全球导航卫星系统（global navigation satellite system，GNSS）卫星作为非合作辐射源,使用合成孔径雷达技术获取地球表面图像[1-2]，在遥感应用[3-6]、目标探测[7-8]、地物识别及地表形变监测[9-10]中变得越来越重要。与GNSS-R 的遥感应用相比，GNSS-R BSAR 可以对地貌及地物纹理特征有很好的展现，因此，可以提取到更加丰富的特征信息提高GNSSR 遥感反演的精度。

与传统合成孔径雷达（synthetic aperture radar，SAR）相比，GNSS-R BSAR 具有明显优势。首先，由于无需额外发射机，使得该技术的设备重量轻、功耗低、成本低；其次，140 多颗在轨导航卫星使得地球任何区域可同时接收超过20 颗卫星的信号，为不同角度的多辐射源融合提供了可行性，可获取观测区域更加丰富的地表特征信息；最后，GNSS 可以提供精确的授时服务，保证了该技术的同步性能。

一站固定模式[11]是GNSS-R BSAR 的主要工作模式之一，通过将接收机安装在地面某高点，或悬停的无人机和空间浮空器上，对固定区域进行合成孔径成像，实施长时间观测。尽管后向投影时域(back projection, BP) 算法可处理任意几何构型且满足长时间合成孔径[1,12]的需求，但BP 算法计算量大，限制了其被广泛应用。相比于BP 算法，距离多普勒(range-Doppler，RD)算法[13]和线性调频变标(chirp scaling，CS)算法[14-15]等频域算法可提高成像效率，但为获得高方位向分辨率，一站固定式通常需几百秒甚至上千秒的合成孔径，回波信号在方位向上不再满足位移不变性，因此文献[13-15]频域算法在长时间合成孔径情况下会产生散焦现象。为了实现一站固定模式下长时间合成孔径GNSS-R BSAR 图像的聚焦，提出一种改进的RD 成像算法，在文献[16]提出的高阶等效斜距模型的基础上，利用直达信号的伪码和载波相位对回波信号的距离徙动和相位误差进行补偿，提高距离徙动校正精度，并采用方位向分块混合相关处理方法进行方位向相位补偿，解决方位向移变导致随方位向位置变化的多普勒调频率问题。

1 GNSS-R BSAR 信号建模

1.1 高阶等效斜视距离模型

导航卫星的椭圆运动轨迹导致导航卫星与目标的精确斜距表达式极其复杂。通常采用二阶等效距离模型、等效斜视距离模型[17]等近似描述卫星与目标的相对运动。二阶等效距离模型是将卫星与目标斜距表达式在多普勒中心时刻进行泰勒展开并保留至二次项。即

尽管理论上等效斜视距离模型较二阶等效距离模型更加精确，但随着合成孔径时间增加，等效斜视距离模型的斜距误差将超过斜距误差阈值，导致方位向散焦，无法满足GNSS-R BSAR 在一站固定模式下长时间的合成孔径需求。为更精确描述导航卫星的运动，本文采用文献[16]提出的高阶等效斜视距离模型计算GNSS-R BSAR 的斜距。该模型表示为

式中：A 为导航卫星的等效加速度。如图1 与图2所示为等效斜视距离模型和本文采用的高阶等效斜视距离模型的斜距补偿误差随合成孔径时间的关系。由图1 可知等效斜距模型的有效合成孔径时长约为50 s，本文采用模型极大提高了斜距精度，如图2 所示，且合成孔径时长为873 s(约14.5 min)以内精度仍满足方位向聚焦要求。

图1 等效斜视模型-斜距误差仿真Fig.1 Equivalent squint range model-slope range error simulation

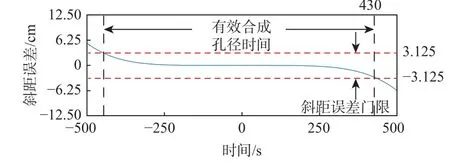
图2 高阶等效斜视距离模型-斜距误差仿真Fig.2 Improved equivalent squint range model-slope range error simulation

1.2 GNSS-R BSAR 信号模型

如图3 所示GNSS-R BSAR 的一站固定模式几何构型，其中 RB(t)为接收机到卫星的瞬时斜距，RT(t)为 目标到导航卫星的瞬时斜距，RR为目标中心到接收机的距离。总斜距为 R(t)=RT(t)+RR。GNSSR BSAR 的接收系统包含1 个直达通道和1 个回波通道。直达通道通过右旋圆极化（right-hand circular polarization，RHCP）全向型天线接收 GNSS 直射信号，并获得准确的载波相位、码相位和定位信息，为反射通道的信号同步提供精确的参考信息。直射信号经正交解调和SAR 数据格式化后的二维形式[18]可表示为

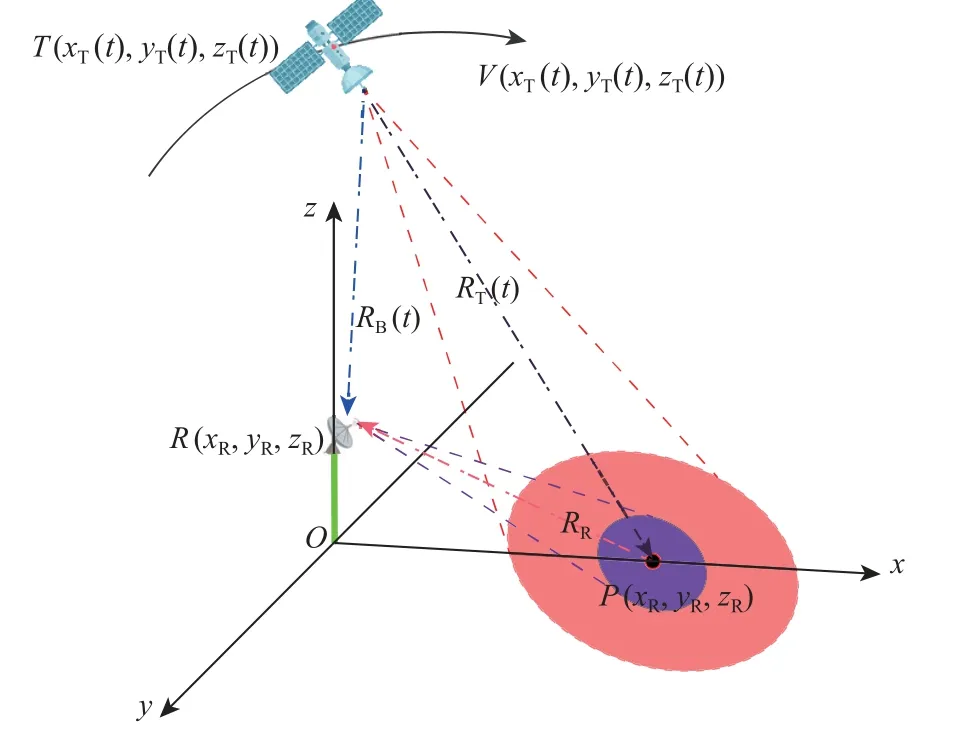
图3 GNSS-R BSAR 一站固定模式的几何构型Fig.3 GNSS-R BSAR one station fixed pattern geometric configuration

2 直反信号协同的RD 成像算法

基于高阶等效斜视模型，本文提出一种如图4所示的直反信号协同的一站固定模式下GNSS-R BSAR 距离多普勒成像算法。首先，对直射信号进行捕获、跟踪、定位获得导航卫星的位置、速度、载波相位及码相位；然后，通过检测直射信号的多普勒相位提取接收机本振频率漂移等引起的相位误差，并将提取出的相位误差在反射通道信号成像的过程中予以补偿，提高成像质量。其中，IFFT 为反傅里叶变换，FFT 为傅里叶变换。

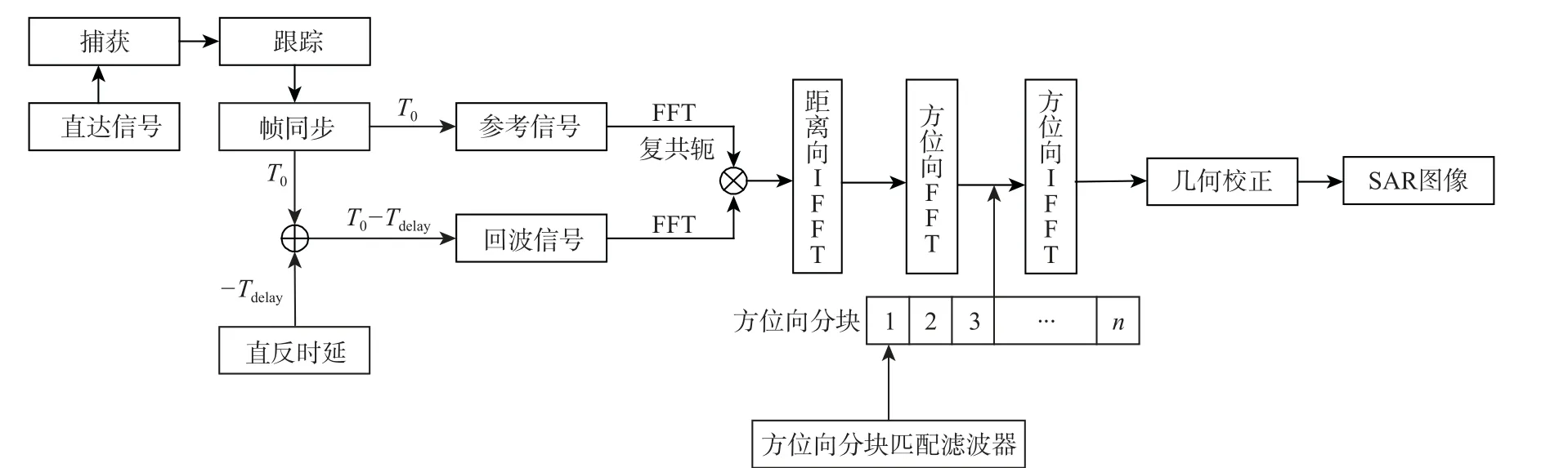
图4 所提算法流程Fig.4 Flowchart of the proposed algorithm

2.1 基于直反协同的距离向压缩

与传统SAR 不同，GNSS-R BSAR 距离压缩通过回波信号和伪随机码自相关实现。以周期为1 ms 和码速率为10.23 MHz 的GPS-L5 信号伪随机码为例，其自相关函数的峰值旁瓣比(peak side lobe ratio，PSLR) 高于35 dB，且在高斯白噪声条件下，自相关增益为40 dB，使得GNSS 接收机可从噪声中检测微弱的导航信号。经距离向自相关后的回波信号为

式中：P(τ)为伪随机码的自相关函数。

由于一站固定模式下GNSS-R BSAR 等效斜视角和导航卫星的多普勒中心频率通常较大，因此，回波信号距离徙动轨迹具有很大的线性项(距离走动)和二次项(距离弯曲)。如果直接进行方位向傅里叶变换，则由于距离向与方位向耦合使得距离向压缩的信号在距离向发生散焦。在传统单站SAR中，通常引入二次距离压缩因子进行距离徙动校正将距离向信号重新聚焦。在GNSS-R BSAR 中，由于导航信号调制了无显式表达式的伪随机码，而非线性调频信号，因此，距离向与方位向耦合的形式与传统单站合成孔径雷达不同，二次距离压缩滤波器的解析式难以获得。本文在方位时域以直达天线的相位中心为参考，通过直射信号的距离徙动信息，对回波场景中的距离徙动对消来进行距离徙动的校正。可以根据卫星位置、目标区域、接收机3 点位置信息计算导航卫星直射信号与回波信号传输的时延差 Tdelay，通过补偿该时延差，可得到导航卫星同一时刻发出的直射信号及反射信号。将距离徙动校正后，只剩下目标到接收机的固定距离项，及微小的残差项。此时再进行方位向傅里叶变换，由于距离向与方位向耦合引起的距离向信号散焦已经消除。经距离徙动校正后的回波信号表达式为

由式(10)可知，残差项主要取决于卫星、场景中心、回波天线相位中心的位置及卫星速度。若残差值的变化在距离向中不超过一个距离门，则不会影响到成像结果。为验证所提算法的边界条件，进行场景参数如表1 所示的仿真分析。仿真中选取真实卫星星历数据，并在笛卡儿坐标系原点架设接收机，目标点设置在x 轴上，目标点间隔为1 m，沿x 轴的正向遍历。

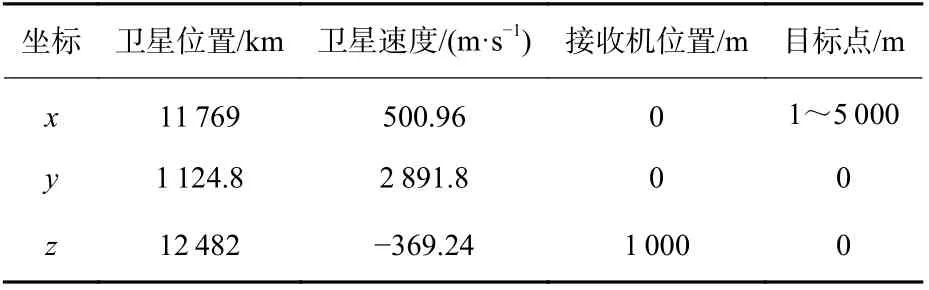
表1 残差项仿真参数Table 1 Residual simulation parameters

如图5 所示，随着合成孔径时间及接收机与目标点距离的增加，残差项误差变大。当回波天线相位中心与目标点距离在5 km 内时，距离徙动校正方法满足长时间合成孔径处理；当回波天线相位中心与目标距离较远时，合成孔径时间60 s 内也可满足距离向压缩要求。

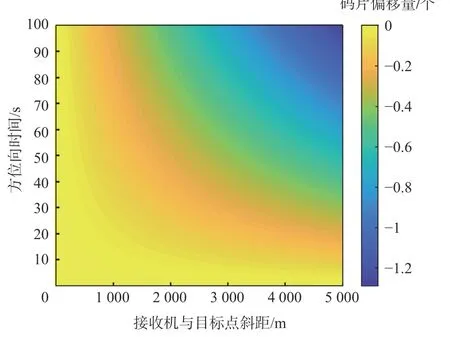
图5 残差与斜距及合成孔径时间的关系Fig.5 Relationship between residual error and slant range and synthetic aperture time

由于GNSS-R BSAR 一站固定式的天线相位与目标点距离通常小于5 km，因此可满足距离徙动校正需求。经距离徙动校正后的回波形式为

2.2 基于分块混合相关的方位向压缩

由于一站固定模式下GNSS-R BSAR 的合成孔径时间过长，高阶等效斜视模型中存在的等效加速度，导致随方位向时间变化的多普勒调频率，因此，回波信号已不再具有方位移不变的性质，同一距离门的信号无法再通过相同的方位向匹配滤波器进行一致压缩。本文采用了方位向分块混合相关的处理方法，动态更新匹配滤波器的调频率参数，解决回波信号方位向移动问题。每一子块的回波信号使用子块中心位置的调频率参数作为子块整体混合匹配滤波器的调频率使得子块中心的方位向相位得到完全补偿。为解决边缘点部分产生的散焦，在处理效率和处理精度之间做一个权衡，设定子块边缘点方位相位误差上限为

3 仿真分析

通过成像仿真进行所提算法有效性的验证。仿真选用信号为GPS PRN03 卫星发射的GPS-L5信号，参数设置如表2 和表3 所示，场景布置如图6所示。方位向混合相关处理时子块的宽度设置为2 km。

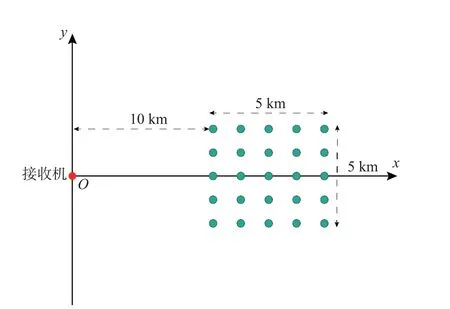
图6 场景点目标分布Fig.6 Scene point target distribution map

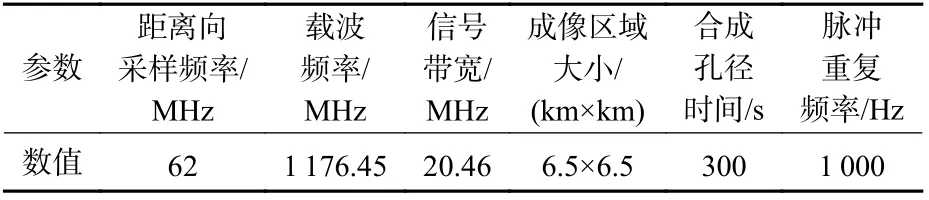
表2 仿真参数Table 2 Simulation parameters

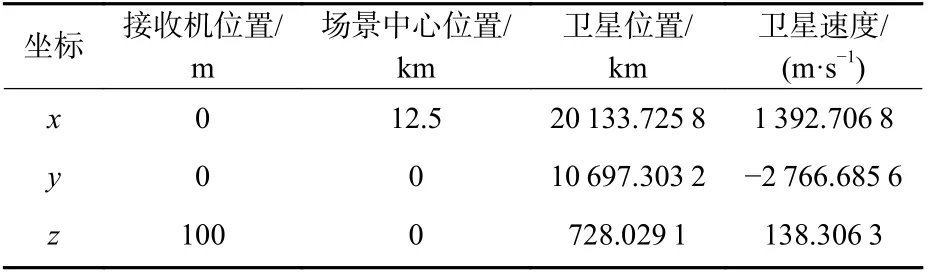
表3 场景参数Table 3 Scene parameters

如图7 所示为所提算法对仿真场景的成像结果。场景中的25 个点目标都被聚焦到了正确的位置。如图8 和表4 所示为点目标13、25 的距离向和方位向成像横截面及其评估结果。点目标 13 位于方位向子块中心点，其方位向和距离横截面与表4 所示的理论结果一致，在距离向和方位向均未出现失真。点目标 25 位于方位向子块的边缘位置，尽管该处目标有最大的残差相位，方位向横截面出现成像的最大程度失真，但从方位向横截面上可看到仅为一个微小失真，主要体现在主瓣展宽，距离向峰值旁瓣比和积分旁瓣比均出现0.20 dB 失真，方位向的PSLR 和积分旁瓣比(ISLR)有0.21 dB的失真。对称的左右旁瓣说明该点残差的线性相位已被补偿掉，残差的相位误差主要是高阶项。

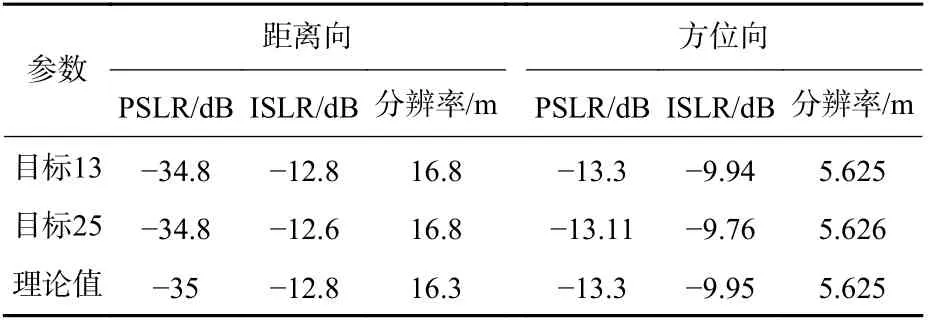
表4 所选点目标的评估参数Table 4 Evaluation parameters of selected point target

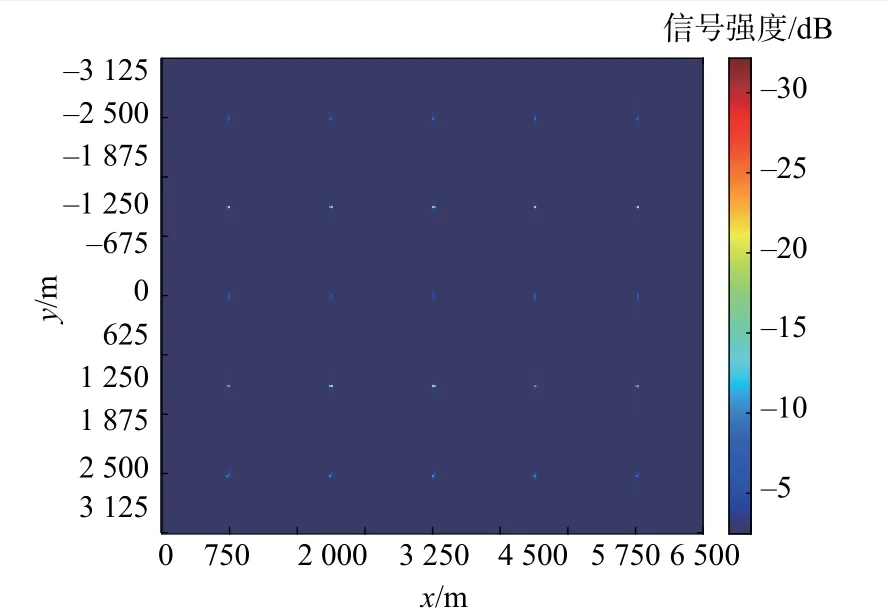
图7 所提算法的成像结果Fig.7 The proposed algorithm imaging results

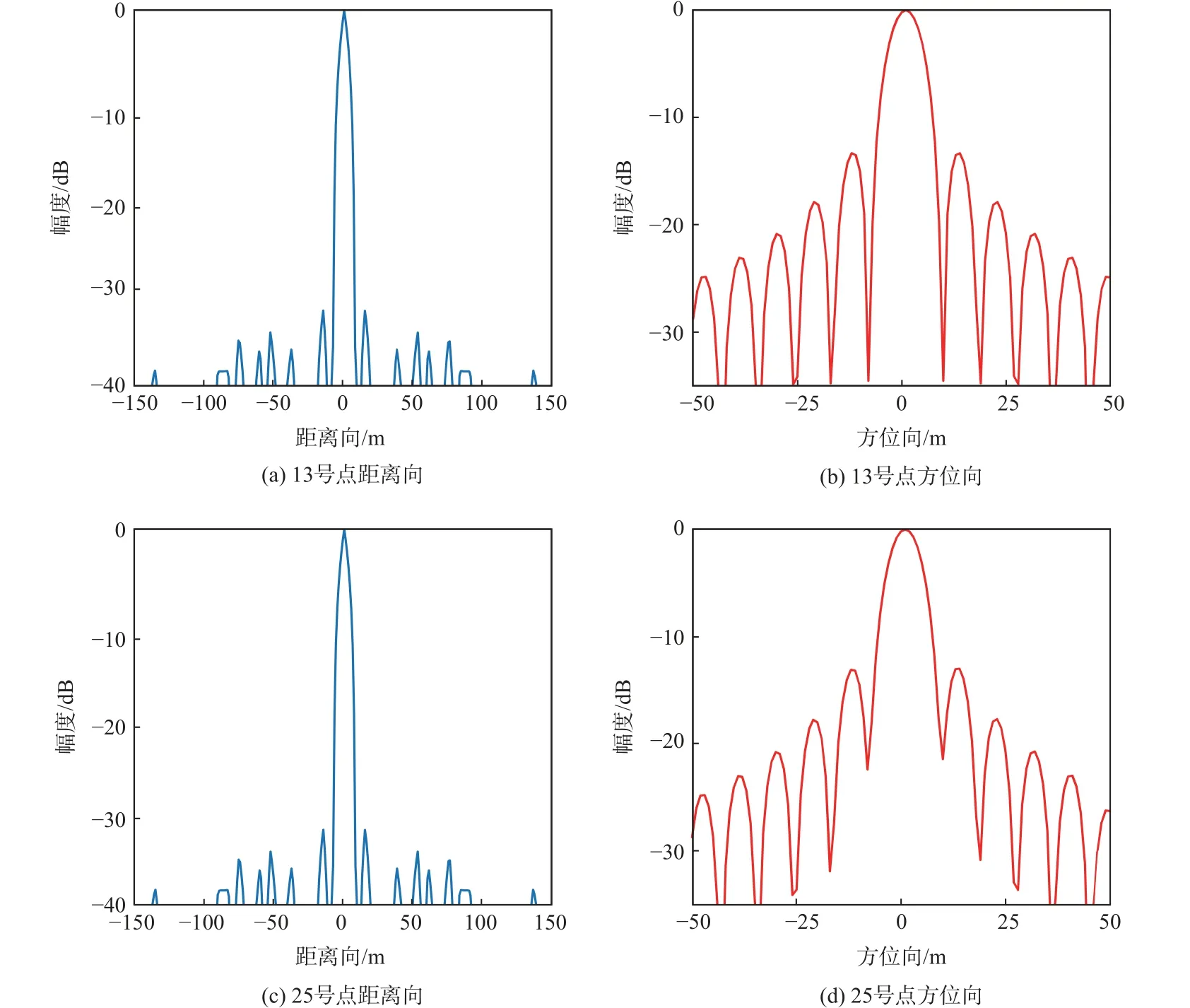
图8 13 号与25 号点目标仿真横截面分析Fig.8 Cross-section analysis of target simulation at No.13 and No.25

4 实验验证

为进一步验证所提算法的有效性，本文开展了如图9 所示基于GPS-L5 信号一站固定模式成像实验。实验场景在如图10 和表5 所示的北京航空航天大学体育场东边的建筑物群。GNSS-R BSAR 成像数据采集系统同时采集直射和目标反射的GPSL5 信号，其中直达信号用增益为3 dB 的全向右旋圆极化天线接收，用于实现导航信号的捕获跟踪定位及与回波信号的同步；目标反射信号用增益为19 dB的左旋圆极化天线接收，用于目标成像。具体的系统参数及成像参数如表6 所示。

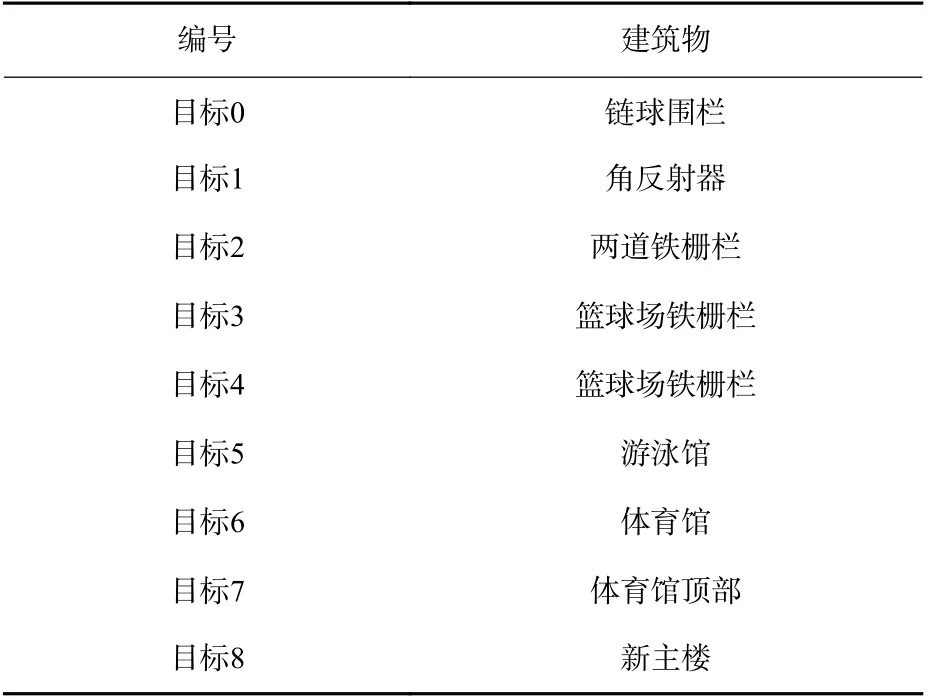
表5 实验场景主要回波目标Table 5 Main echo target of experimental scene

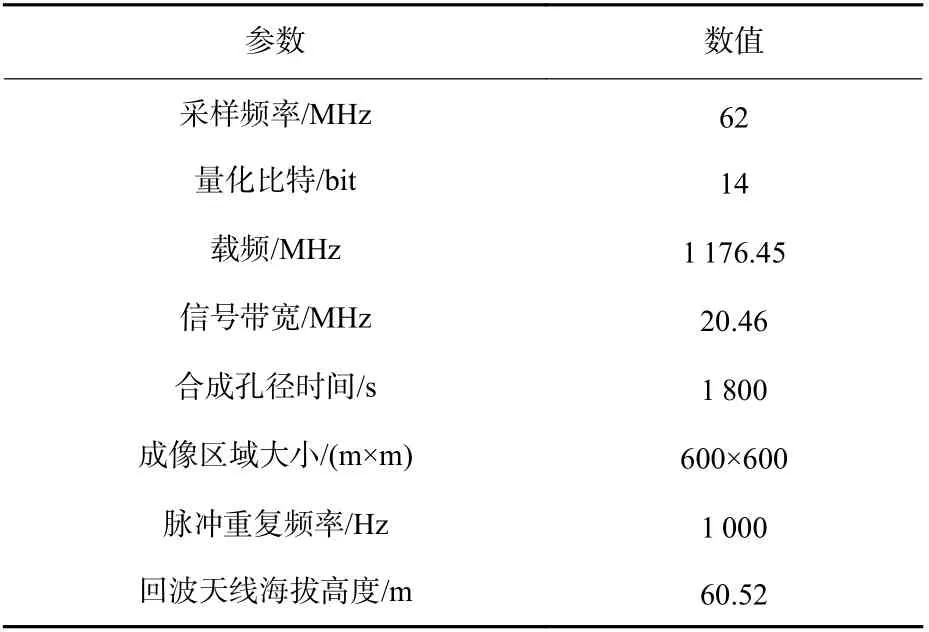
表6 数据采集系统及成像参数Table 6 Data acquisition system and imaging parameters

图9 GNSS-R BSAR 数据采集系统Fig.9 GNSS-R BSAR data collection system

由于GPS PRN03 卫星与地面固定接收机构成较好的双基构型，可使GNSS-R BSAR 图像具有较好的距离向分辨率，因此，本次实验选用GPS PRN03卫星信号作为辐射源。合成孔径中心时刻GPS PRN03 卫星在站心坐标系下的位置和速度信息如表7 所示。

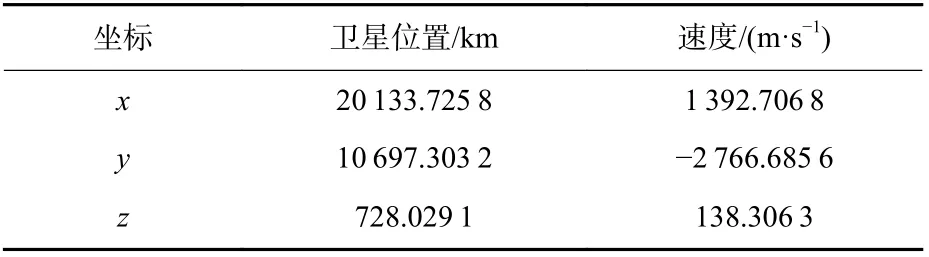
表7 GPS PRN03 卫星的位置和速度信息Table 7 GPS PRN03 satellite position and speed information

对采集数据用所提算法和传统BP 算法进行合成孔径时长为1 800 s 的成像。成像结果如图11 与图12 所示，可看出2 种算法获得图像非常相似，说明2 种算法的成像能力相似。尽管经过长时间的合成孔径，GNSS-R BSAR 的方位向分辨率达到了亚米级，但是GPS L5 信号的带宽为20.46 MHz，其准单站模式的距离向分辨率约为15 m，在双站模式下，受几何构型的影响，比准单站的距离向分辨率更差。因此，现有的GNSS-R BSAR 图像无法达到光学图像一样的直观解析能力，需要进行雷达图像的解释。为了表征其分辨能力这里将获得雷达图像与光学图像进行了基于位置信息的匹配，结果如图13 所示。由于回波天线与目标场景的高度近似相同，且GPS PRN03 卫星和接收机都位于目标区域的西侧，导致场景中建筑物主要的回波信号来自于西部边缘部分。因此，在图13 中雷达图像的强散射回波都聚焦到了建筑物的西侧。图10 中的9 个建筑物都被聚焦到了雷达图像正确的位置，链球围栏回波是由线的旁瓣接收，因此，在图像中聚焦的能量较弱。其他建筑物为天线的主瓣接收均显示了良好的聚焦效果。

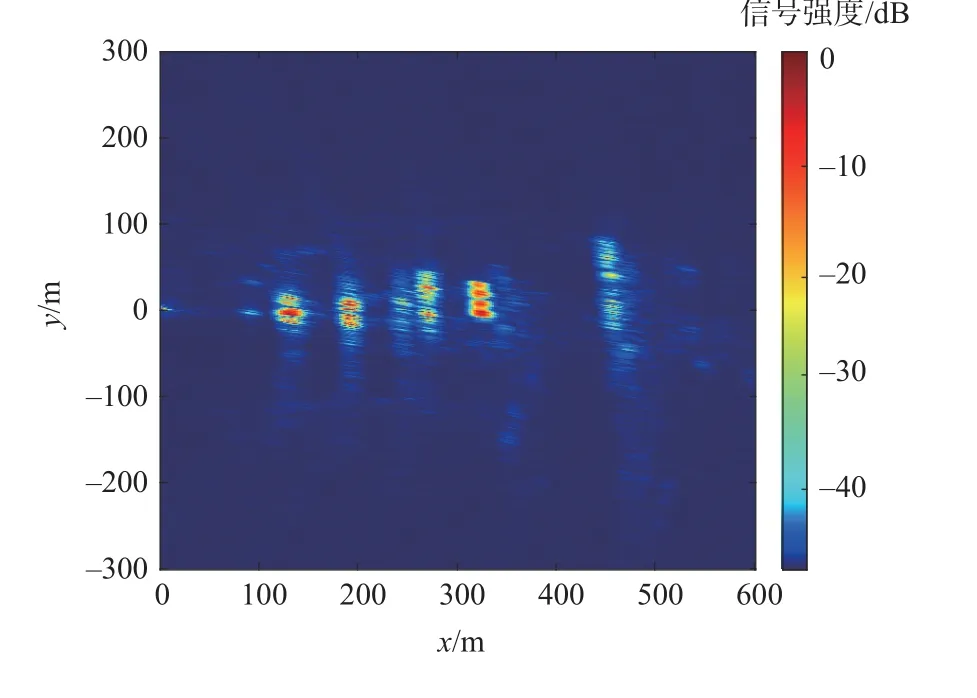
图12 所提算法成像结果Fig.12 The proposed algorithm imaging results

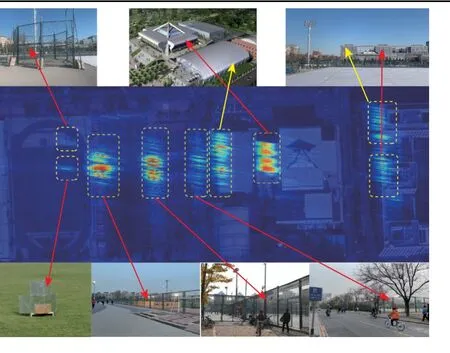
图13 所提算法成像结果光学匹配图Fig.13 The proposed algorithm imaging result optical matching map

为了进一步评估所提算法获得成像质量和计算复杂度，将所提算法与BP 算法进行了对比分析。本文分别对2 种算法获得的图像进行了交叉横截面的分析。选择了以体育馆西部边沿部分进行剖析，因为该区域的回波信号能量较强且连续性较好。如图14 和图15 所示，所提算法和BP 算法无论在距离向还是方位向的聚焦效果都是相当的。以体育馆边沿处沿距离向进行了测量分辨率约为16.8 m，与理论值一致。在1 800 s 的合成孔径下，方位向分辨率达到了亚米级，实验中无法直接对方位向的分辨率进行测量，这里通过测量体育馆的物理长度进行评估，由图15 可以看出，方位向的测量值为40 m 与光学测量值一致。实验结果说明了所提算法的成像性能与时域算法成像性能相当。

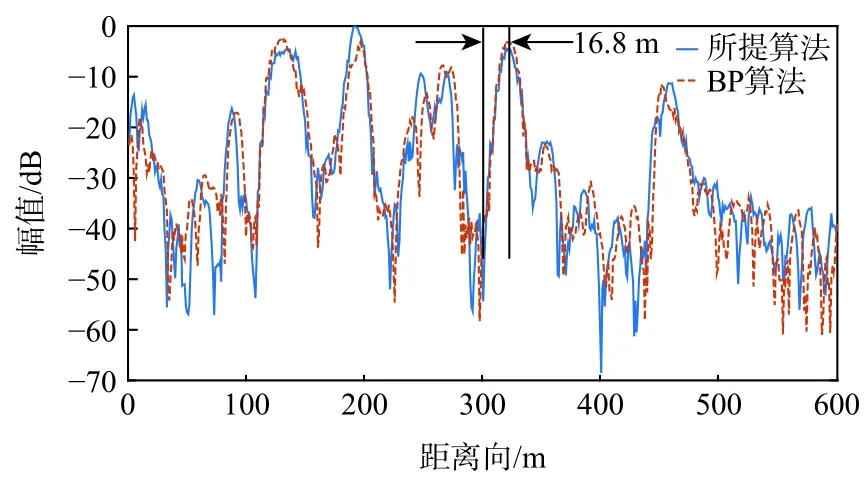
图14 成像结果交叉横截面的分析-距离向剖面Fig.14 Analysis of cross-section of imaging results-range profile

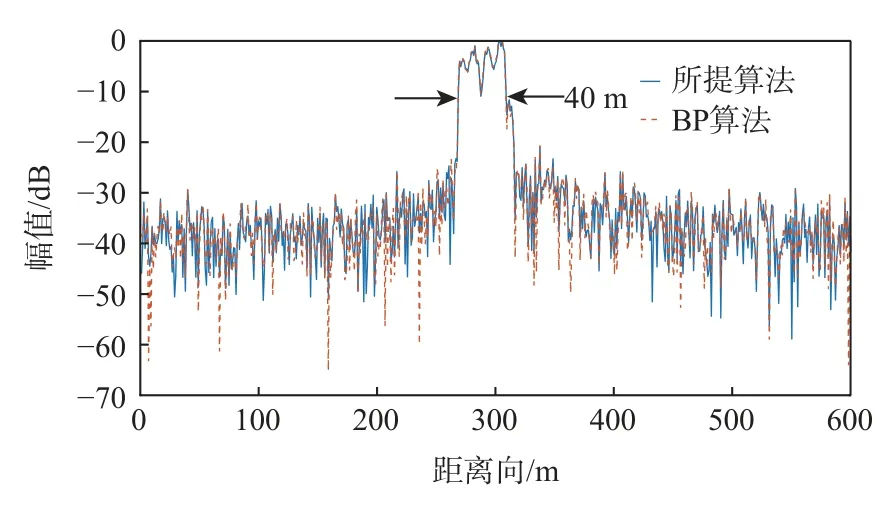
图15 成像结果交叉横截面的分析-方位向剖面Fig.15 Analysis of cross-section for imaging results-azimuth profile

本文所提算法的整个成像过程执行了4 次距离向FFT, 2 次方位向FFT,1 次复数乘法，整个所提算法的计算复杂度可以表示为

式中：Nr和 Na分别为距离向和方位向的采样点数。BP 算法的距离向压缩过程中需要执行4 次距离向FFT 和1 次复数乘法，其计算量为 4 NrNalog2Nr，后向投影的过程中计算量可以表示为 NiNxNyNa, 其中，Nx和 Ny为成像区域的2 个维度的像素点个数，Ni为像素点间隔。整个BP 算法的计算复杂度可以表示为

由式（17）可以看出，随着成像区域和合成孔径时间的增加，BP 算法的计算量会急剧增加。在本次实验中，相同的计算平台（处理器为AMD-3800 X@3.8 GHz, 8 核心16 线程，内存为64 GHz），所提算法的计算时间为350 s 左右，BP 算法的计算时间为19 880 s 左右，计算效率提升了56.8 倍。实验结果验证了所提算法的可行性和高效性。

5 结 论

1) 针对GNSS-R BSAR 的一站固定模式，提出了一种改进的距离多普勒算法。首先，通过引入改进的等效斜视距离模型，改善了长时间合成孔径导致的方位向散焦的问题；其次，利用导航信号良好的同步性能，通过直射与回波信号时域对消的方式，完成了距离徙动校正；最后，通过方位向分块混合相关的算法，提高了方位向的聚焦精度。

2) 基于系统空间分辨率的考量，在仿真与实验验证中采用GPS PRN03 卫星发射的GPS-L5 信号。仿真结果表明，所提算法在成像质量和效率方面均表现良好。在1 800 s 合成孔径的实测中，距离向的分辨率为16.8 m，方位向分辨率达到了亚米级，该分辨率可以满足大部分遥感测量的需求。所提算法与传统的BP 成像算法相比，在一站固定模式下成像质量相当，在效率方面远优于传统的 BP算法。