基于机器学习算法的樟子松立木材积预测

孙铭辰，姜立春

(东北林业大学林学院，森林生态系统可持续经营教育部重点实验室,黑龙江 哈尔滨 150040)

立木材积是森林资源调查的重要指标，也是计算森林蓄积量和生物量的主要依据[1-4]。因此，在森林经营管理中评价经济效益和生态效益时，立木材积的研究一直以来都备受关注。传统立木材积的计算通常利用已知的一元、多元立木材积表，或通过拟圆锥法、质心法、重要性采样法等进行估测[5-6]。随着人们对森林资源调查的不断深入，针对不同地区不同树种相继建立了不同类型的材积模型[7-8]。但森林生长是一个复杂连续且具有随机性的非线性生长过程，通过拟合立木材积模型虽然能填补材积预测的空白，但受制于模型和变量的选择以及对模型先验知识的累积，且预测精度受区域变化影响较大，增加了森林资源调查和经营管理的难度。

机器学习算法理论始于20世纪中叶，相比传统模型，机器学习算法可以在没有先验知识的前提下对数据进行拟合，分析数据中不同变量之间复杂、动态的内部结构[9]，而且机器学习算法的适用性更广，应用更加方便，能很好地克服数据中可能存在的缺失点、噪音、多重共线性和异方差等现象[10]，在生物遗传、信息技术和金融工程等领域已有广泛应用。近年来随着统计软件技术的发展，机器学习算法在林业上也得到了一定的应用。Guan等[11]通过胸径及其年增长量建立4种人工神经网络模型，成功地对红松的生存率进行了预测；Maria[12]通过人工神经网络模型估算树皮材积，发现相比于非线性模型的均方根误差(RMSE)降低了6.02%；Maria等[13]通过对比分析不同的非线性模型和ε-支持向量机回归模型对4种黑凯木树皮材积的预测，得出ε-支持向量机回归模型的Furnival 指数(FI)值分别比3种非线性模型均有所降低，且与真实值更接近。Colin等[14]结合LiDAR数据建立多个模型对森林生物量进行估算，结果表明支持向量机回归为最优模型。目前，已有部分机器学习算法应用于立木材积中[15-19]，但鲜有对不同类型算法同时进行对比和分析的研究。

本研究以大兴安岭樟子松(Pinussylvestrisvar.mongolica)为研究对象，利用Matlab 2019b软件建立3种目前应用较为广泛的机器学习算法：反向神经网络模型(back propagation，BP)、ε-支持向量机回归模型(ε-support vector regression，ε-SVR)和随机森林模型(random forest，RF)，并与传统二元材积模型作对比，评价最优模型，以期为提高樟子松的立木材积预测精度和科学经营提供理论依据。

1 材料与方法

1.1 数据来源

供试樟子松来源于大兴安岭图强林业局(122°18′28″～123°28′10″E，52°15′35″～53°33′42″N)。将树木伐倒后测量其带皮胸径、树高，并对15个相对树高的带皮直径，利用区分求积法计算樟子松带皮立木材积。通过散点图排除异常点后得到184株样木，以5 cm为一个径级分为10个径阶，按7∶3分径阶随机抽样。最终得到训练样本129株、测试样本55株。样木调查统计量如表1所示。

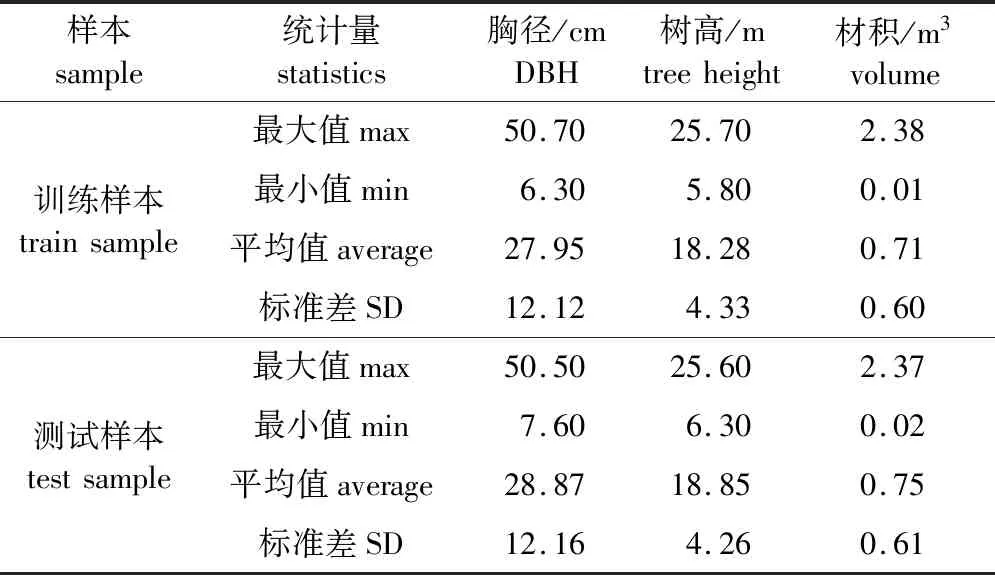
表1 樟子松调查因子统计量Table 1 Survey factor statistics of Pinus sylvestris var.mongolica

建模前对样本数据进行min-max标准归一化处理，使其统一介于[0,1]，得到的泛化结果通过反归一化还原，并与真实值对比和评价。

1.2 模型建立方法

1.2.1 二元材积模型

传统立木材积方程包括一元、多元线性和非线性模型，采用林业上应用较为广泛的非线性二元材积模型(non-linear regression models，NLR)作为立木材积计算公式[20-21]。

V=a0Da1Ha2。

(1)

式中：V为材积；D为胸径；H为树高；a0、a1、a2为方程的参数。

1.2.2 反向神经网络模型

反向神经网络模型(back propagation，BP)是由输入层、隐含层和输出层组成的反向传播网络模型，不同层通过神经元相互连接，但相同层神经元互不相连。通过激活函数将上一层的输入转化为下一层的输出，如输出结果超出期望误差，则通过误差逆向传播算法修正各神经元函数的权值和阈值，并不断重复上述过程以达到降低误差的目的[22]。经研究表明，3层BP神经网络即可拟合任何非线性曲线。

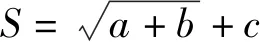
选用目前较为常用的几种训练算法：①梯度下降算法，包括变学习率动量梯度下降算法(GDX)、变学习率梯度下降算法(GDA)、弹性梯度下降算法(RP)；②共轭梯度算法，包括Powell-Beale共轭梯度算法(CGB)、Fletcher-Reeves共轭梯度法(CGF)、Polak-Ribiere共轭梯度法(CGP)、Scaled共轭梯度算法(SCG)；③拟牛顿及其他优化算法，包括拟牛顿算法(BFG)、一步正割算法(OSS)、Levenberg-Marquardt算法(LM)。

1.2.3ε-支持向量回归模型

ε-支持向量回归模型(ε-support vector regression，ε-SVR)是一种基于结构风险最小化原理的超平面模型。通过核函数将低维空间中难以区分的向量通过非线性变换映射至高维空间中使其线性可分，借助惩罚因子(C)和核参数(gamma)降低数据与超平面之间的残差，以达到提高模型精度的目的[17]。因此改变核函数类型以及C、gamma参数可以有效降低误差，得到最优ε-SVR模型。常用的核函数方法包括线性核函数(line)、多项式核函数(polynomial)、径向基核函数(RBF)等。其中C、gamma参数通常选用网格搜寻法，即设定两个参数的范围，按一定步长进行组合建模。但这种方法费时费力且精度不高，因此本研究选用遗传算法(genetic algorithm，GA)进行参数寻优。

GA是通过模拟物种进化过程研发的一种全局搜索优化算法。通过生成一个初始群体并对数据进行编码、选择、杂交、变异，不断生成新的组合，计算每个组合的适应度，通过“优胜劣汰”的方法不断筛选最优个体，并以适应度达到最大时的结果作为最优参数，以十折交叉检验对参数的解释能力进行评估。综上所述，GA是一种通用性很强的参数寻优方法，在机器学习中也有着广泛的应用[24]。

1.2.4 随机森林回归模型

随机森林回归模型(random forest,RF)是一种基于bagging回归的集成学习算法。通过对样本数据进行随机且有放回重复采样得到多个样本组合，并通过节点分裂和随机特征变量的随机抽取形成多个决策树构成“森林”，对每个决策树得到的结果进行加权平均，作为样本的回归结果[25]。由于每次采样中总有大约1/3的样本未被选用，它们被称为袋外数据(out-of-bag，OOB)。因此可利用这部分数据计算袋外错误率(out-of-bag error)代替交叉检验作为验证模型泛化能力的标准，使得随机森林可以有效地避免过拟合现象[26]。

通过控制变量的方法对决策树个数(ntree)、最小叶子大小(minleaf)、随机抽取变量个数(mtry)3个参数进行寻优，以得到最优的RF模型。其他参数均选用软件默认设置。

1.3 模型评价与检验指标

选用决定系数(R2)、平均绝对误差[MAE，式中记为σ(MAE)]、均方根误差[RMSE,式中记为σ(RMSE)]、相对均方根误差[RMSE%,式中记为σ(RMSE%)]评价模型拟合和预测的能力，并通过平均相对误差[MRB，式中记为σ(MRB)]检验模型预测偏差的大小。为评价模型的无偏估计能力，选用z检验判断模型泛化结果与真实值是否存在显著差异[19]。

(2)

(3)

σ(RMSE%)=σ(RMSE)×100%；

(4)

(5)

(6)

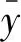
2 结果与分析

2.1 NLR模型的拟合结果

通过最小二乘法得到3个参数分别为a0=3.706 0×10-5，a1=1.512 6，a2=1.566 2。最终二元材积表达式为V=3.706 0×10-5D1.512 6H1.566 2。

2.2 BP模型的拟合结果

通过胸径D、树高H和材积V建立3层BP模型，采用十折交叉检验的方法对训练样本分别进行算法优选和神经元参数寻优。为保证不同算法在统一标准下对比分析，模型的其他参数统一设置如下：隐含层神经元个数为8、最大训练次数为2×103、训练目标误差为1×10-5、学习速率为0.05、动量为0.9，其余参数均采用软件默认数值，并采取提前终止的办法防止模型过拟合。

各算法结果如表2所示，可以看出在3种梯度下降算法中RP算法的4个评价指标均明显优于其他两种。通过比较可以看出4种共轭梯度算法的精度总体差距不大，其中CGF算法的R2略高于其他三者，但在RMSE、RMSE%、MAE的表现不如CGB算法，拟合误差相对较大。在其他3种优化算法中LM算法拟合优度和误差检验均为最佳，相比于其他算法R2提高1.13%～5.26%，RMSE降低13.12%～39.81%，RMSE%降低17.41%～42.46%，MAE降低14.97%～45.94%。因此将LM算法作为BP模型的训练算法。

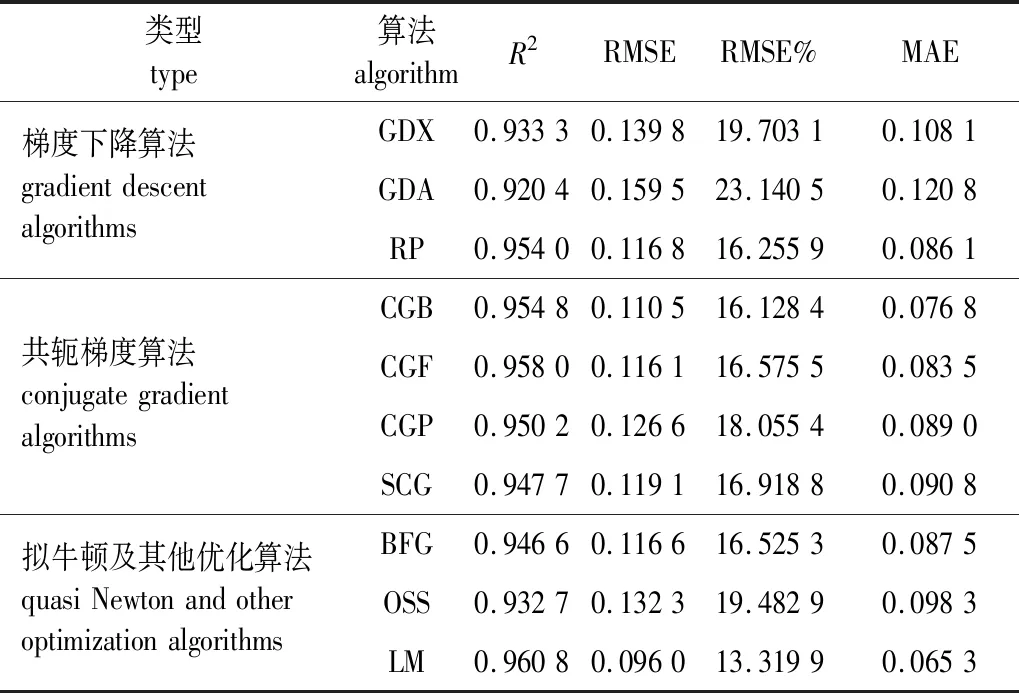
表2 不同算法下BP神经网络拟合精度Table 2 Fitting accuracy of BP neural network with different algorithms

根据经验公式计算可得隐含层神经元个数在3～12之间，通过试错法依次建模比较，在隐含层神经元个数为7时模型R2最高且RMSE最低(图1)。综上所述，最优BP模型为训练算法-输入变量-神经元个数-输出变量(LM-DH-7-V)。

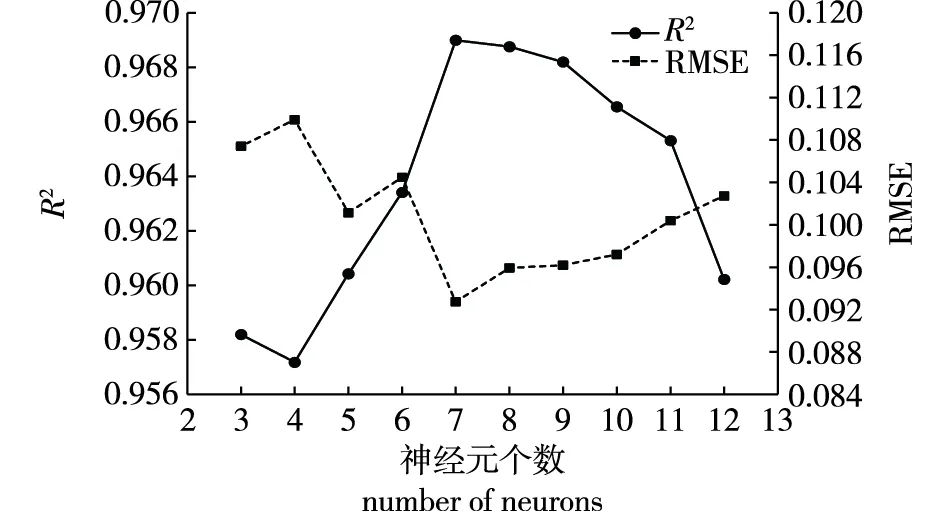
图1 不同神经元的BP模型精度对比Fig.1 Comparison of BP model accuracy of different neurons

2.3 ε-SVR模型的拟合结果

ε-SVR通过核函数将数据映射至高维空间中，寻找样本期望风险最小的最优超平面实现线性回归。采用遗传算法对3种常见的核函数[线性核函数(line)、多项式核函数(polynomial)、径向基核函数(RBF)]进行参数寻优，具体参数设置如下：最大进化数为200、种群进化数量为20、变异值为0.9、不敏感损失参数p=0.01、惩罚因子C搜索范围(0，30)、核参数gamma搜索范围(0，10)，并通过十折交叉检验得到3组最优的模型参数。

各模型结果如表3所示，可以看出精度最高的核函数是RBF，其次是polynomial和line核函数。RBF相比于多项式函数和线性核函数R2分别提高1.80%和11.11%，RMSE降低21.46%和52.82%，RMSE%降低21.44%和52.83%，MAE降低31.69%和59.02%，由此可见RBF不仅可以提高拟合能力，还能很好地降低误差，故选用RBF作为ε-SVR模型的核函数并建立模型。

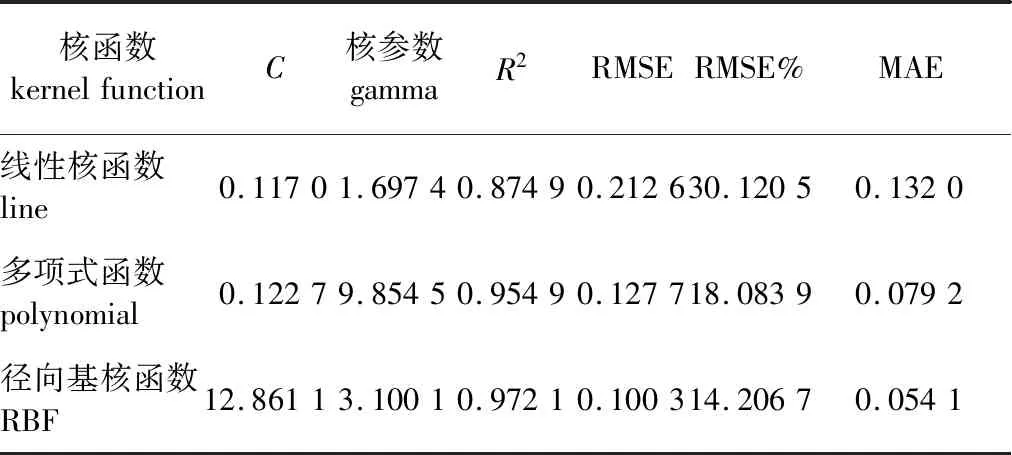
表3 不同核函数下的模型参数和拟合精度Table 3 Model parameters and fitting accuracy under different kernel functions

2.4 RF模型的拟合结果

RF是通过构建多个决策树(ntree)随机选取不同的变量(mtry)，并以每个决策树最小叶子节点(minleaf)均值作为模型最后回归的结果，因此参数的大小直接影响模型拟合的精度。经研究发现，模型误差大小随ntree增加而逐渐减少至某一定值后，便不再发生变化。因此为确保模型充分训练，预设ntree个数为2 000。采用控制变量的方法测定最优minleaf的数量，在默认mtry值下对比minleaf为1、3、5、10、20时的OOB误差值。结果如图2所示，可以看出随着minleaf值逐渐减小，模型的误差也逐渐减小，因此得出最优的minleaf值为1。同时从图2A中也可以看出，当ntree大于100后，OOB误差基本不再下降，意味着在建立100颗决策树后模型已完成了训练。为缩短训练时间，提高模型运行的效率，故将ntree的值调整为100。

由于模型的输入变量只有2个，故mtry的取值范围为[1,2]，调整参数后对不同mtry值重新建立模型，由图2B所示两条误差曲线随着ntree的提高最终重叠在一起，说明改变mtry值不会对模型误差产生影响。但是在拟合过程中可以看出，当mtry为2时模型收敛速度明显优于mtry为1，故mtry值设置为2。

图2 不同minleaf和mtry下随机森林的OOB误差曲线(MSE为归一化后的模型误差)Fig.2 The OOB error curve of random forest under different minleaf and mtry (MSE is the normalized model error)

2.5 模型评价与检验

选用最优参数对训练样本建模，并用测试样本验证模型的预测能力。结果如表4所示，机器学习算法无论在拟合和预测中均明显优于传统的二元材积模型，且机器学习算法中训练样本与测试样本的精度差异不大，证明模型并未发生过拟合现象。通过训练样本得到的拟合评价结果可以看出，4种模型的R2均高于0.96，且RMSE均低于0.12，说明模型都具备较好的拟合能力。其中RF模型表现最好，相比于NLR、BP、ε-SVR模型，R2分别提高3.43%、2.05%、2.45%，RMSE降低67.30%、59.40%、62.31%，RMSE%降低67.29%、59.38%、62.28%，MAE降低71.48%、60.96%、59.52%。通过计算MRB可以看出，所有模型的拟合结果均略高于真实值，其中RF模型的偏差最小。对4种模型的拟合评价作对比，除在MAE中ε-SVR略优于BP模型，其余检验精度均满足RF>BP>ε-SVR>NLR。

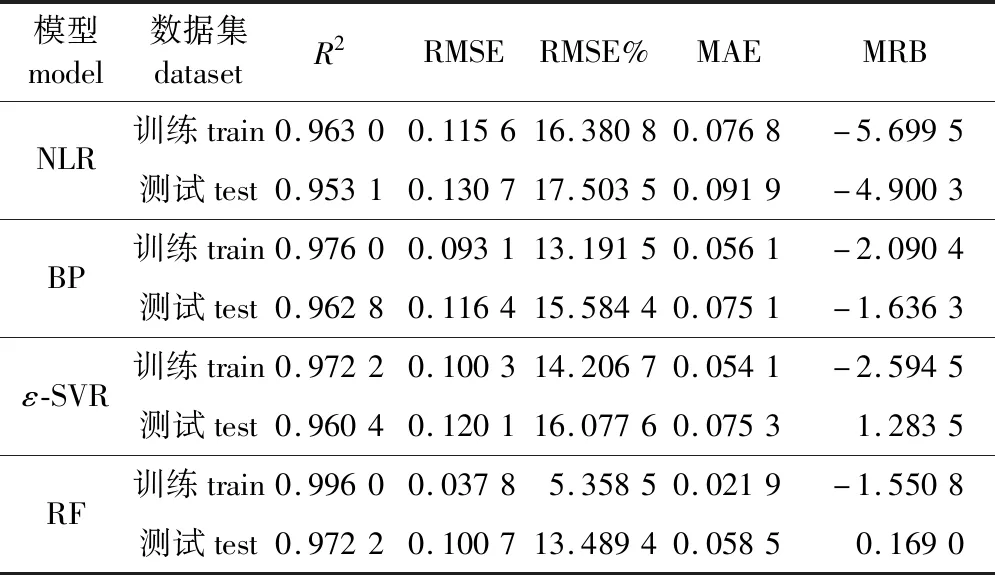
表4 模型拟合和预测结果评价Table 4 Model fitting and prediction result evaluation

根据已建立的模型对测试样本预测，可以看出4种模型都有较好的预测能力，R2均高于0.95，RMSE均低于0.14，且与拟合结果相同，精度均满足RF>BP>ε-SVR>NLR。相比于其余三者，RF模型的R2分别提高2.00%、0.98%、1.23%，RMSE降低22.95%、13.49%、16.15%，RMSE%降低22.93%、13.44%、16.10%，MAE降低36.34%、22.10%、22.31%。结合模型预测结果图(图3)和MRB发现，NLR与BP模型的预测结果略高于真实值，ε-SVR与RF的预测结果略低于真实值，通过比较MRB绝对值可知二元材积模型的预测偏差最大，RF模型偏差最小。

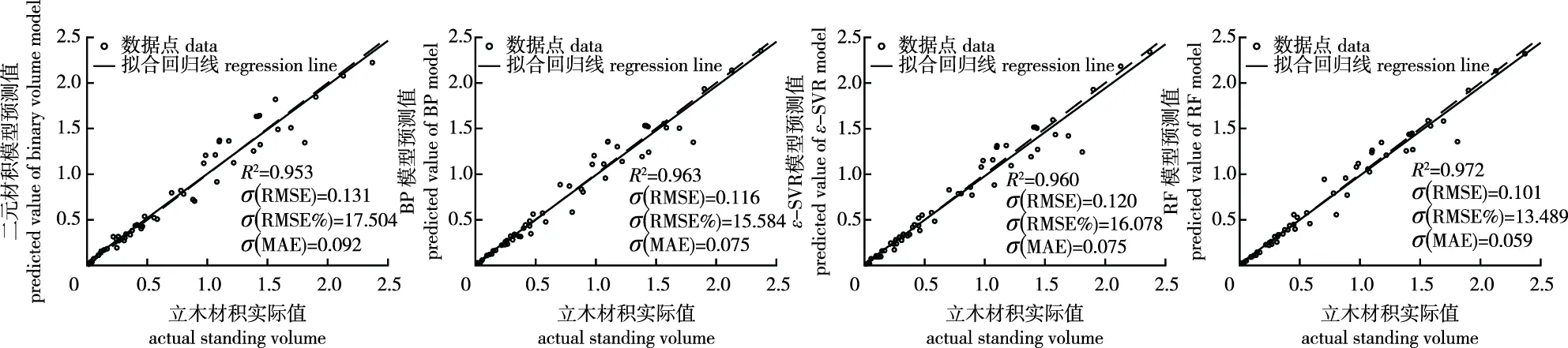
图3 4种模型预测线性回归拟合图Fig.3 The prediction results of four models

为客观评价模型的无偏估计能力，故对模型的拟合和预测结果进行置信度为95%的z检验，以验证泛化结果与真实值的分布是否一致。如表5所示，可以看出4种模型的P值均远大于0.05，故保留原假设，即结果与真实值不存在显著差异。

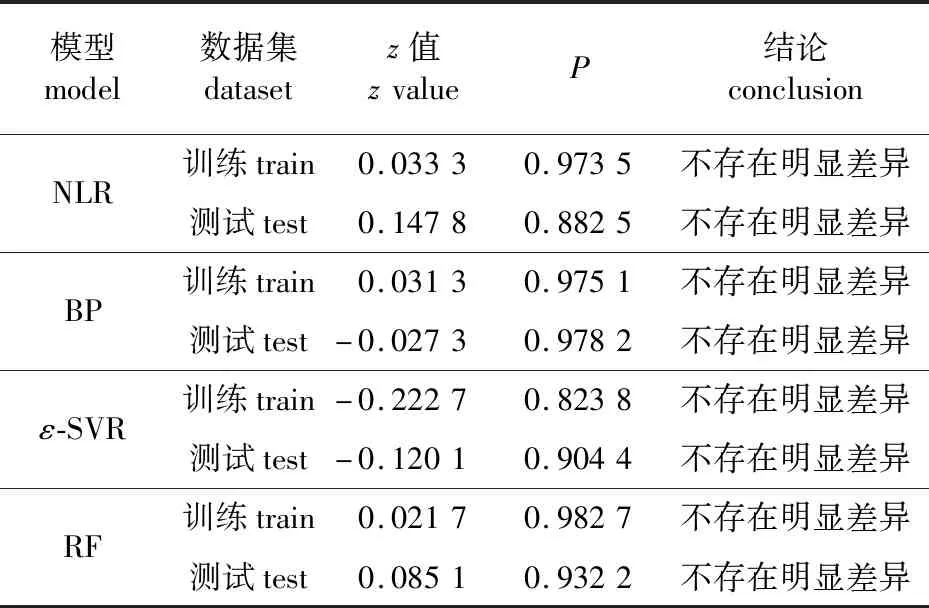
表5 模型的z检验结果Table 5 Z-test results of the model

综上所述，RF为预测大兴安岭樟子松立木材积的最优模型。

3 讨 论

利用大兴安岭184株樟子松单木材积数据建立传统二元材积模型，并与3种常见的机器学习算法进行对比。研究结果表明，机器学习算法可以更好地预测大兴安岭樟子松材积。通过对测试样本的预测结果对比分析可以看出，预测精度大小排序为RF>BP>ε-SVR>NLR。其中，RF模型的预测精度最高，相比于传统模型，RF模型的R2提高2.00%、RMSE降低22.95%、RMSE%降低22.93%、MAE降低36.34%，且与真实值相比偏差更低。通过减少训练样本后重新建模，RF模型精度仍高于传统模型，由此可以看出RF模型在樟子松立木材积预测中的优越性。其余两种机器学习算法中，BP模型虽略优于ε-SVR但与RF模型仍有较大差距。这是因为BP模型所选用的LM算法与ε-SVR更适用于中小样本[27-28]，而建模所选用的样本数量相对较大，此时RF模型在大样本中的适应性优势才被凸显出来。但RF模型同样存在一定的缺点，在处理噪声较大或小样本中易发生过拟合现象[9]，因此在面对此类问题时应先对数据做预处理，避免对模型精度造成影响。

与机器学习算法相比，传统模型虽然可以通过建立回归方程的方式清晰地表达不同变量间相互影响的关系，但通常需要满足很多检验条件作为假设前提，例如正态性检验、独立性检验、异方差检验等，因此不能同时解释复杂的森林生长因子，且不容易对含有噪声的大尺度数据进行拟合。随着近年来科学技术的发展，机器学习算法的出现很好地解决了传统模型的问题。在其他立木材积的研究中也证明了本研究的结果。Maria等[15]和Bhering等[19]发现不同神经网络模型估算立木材积的精度均高于传统的线性或非线性模型，Mushar等[18]在对比不同的机器学习算法与传统模型后发现神经网络模型的精度在分类树种材积比较中精度最高，而在全部类型树种材积比较中支持向量机最高。Wu等[17]运用LiDAR数据对立木材积进行估算，得出3种机器学习模型精度均高于传统模型的结论，其中支持向量机精度高于随机森林，这与本研究结果略有差异。

虽然机器学习算法目前仍存在一些问题，比如参数寻优没有统一的标准、无法掌握数据在黑箱中运行的过程、易产生过拟合现象[11,29]等，但关于机器学习算法的研究还有广阔的进步空间。总而言之，机器学习算法作为一种新兴的建模方法，在大兴安岭樟子松立木材积的预测中相比传统的二元材积模型有着明显的优势，在森林经营管理中是一种有效的替代方案。