基于滑模控制的无人驾驶自行车设计与仿真

2023-03-29刘佩佩周亚丽张奇志

计算机仿真 2023年2期

刘佩佩，周亚丽，张奇志

(北京信息科技大学自动化学院，北京 100192)

1 引言

自行车是日常生活中非常普遍且通用的两轮交通工具，具有静态不稳定和动态可稳定特性。因此自行车已经成为一种对平衡性与稳定性分析和研究的重要实验平台。

1899年Whipple[1]首次运用数学方程描述了自行车的运动行为，并提出了自稳定的概念。自此之后，随着计算机时代的到来，越来越多的研究者借用计算机仿真等工具对复杂问题进行仿真和分析，由此开始了对无人驾驶自行车的深入研究。郭磊，黄用华等人[2-3]基于部分反馈线性化原理，以各自所设计的试验样机为平台，实现了多种无人驾驶自行车的平衡运动。Shafiekhani[4]等人采用了基于神经模糊控制器的无人驾驶自行车平衡控制方法，获得了较好的控制效果。2019年，清华大学类脑计算研究中心施路平教授团队在《自然》上发表的文章中，搭载天机芯的无人驾驶自行车也瞬间火爆网络[5-6]。2020年，刘延柱教授[7]讨论了无人驾驶自行车稳定行驶的实现可能性，对前叉受控的自行车数学模型做了稳定性分析，进一步表明前叉转轴系统对自行车稳定性的重要影响。

总结前人的研究经验，本文从自行车前叉转向系统的设计出发，设计一种基于曲柄滑块机构控制的无人驾驶自行车，实现了对转向电机输出力矩的放大作用，并通过设计滑模控制器对系统进行了仿真验证。

2 系统动力学模型建立

2.1 无人驾驶自行车系统描述

图1所示为无人驾驶自行车系统结构模型图。假设系统所有的质量集中于质心上，定义质心高度为h，质心在水平面上的投影点与后轮着地点的距离定为b，前轮质心到前车把转动轴的距离为λ，车身与z轴的夹角为车体倾角β，前车把转轴与x轴的夹角为前车把转角δ，定义逆时针方向为正方向。定义车体倾角和前车把转角均为零时的滑块位置为起始位置；起始位置时曲柄滑块机构可看成是一个直角三角形，定义直角短边、即曲柄为c(始终与前车把保持平行共面)，直角斜边、即连杆为a，这两条边的长度为定值、可测量；定义滑块位置边长度为x。系统启动瞬间，自动调整配重块位置，保证车体处于直立平衡状态。

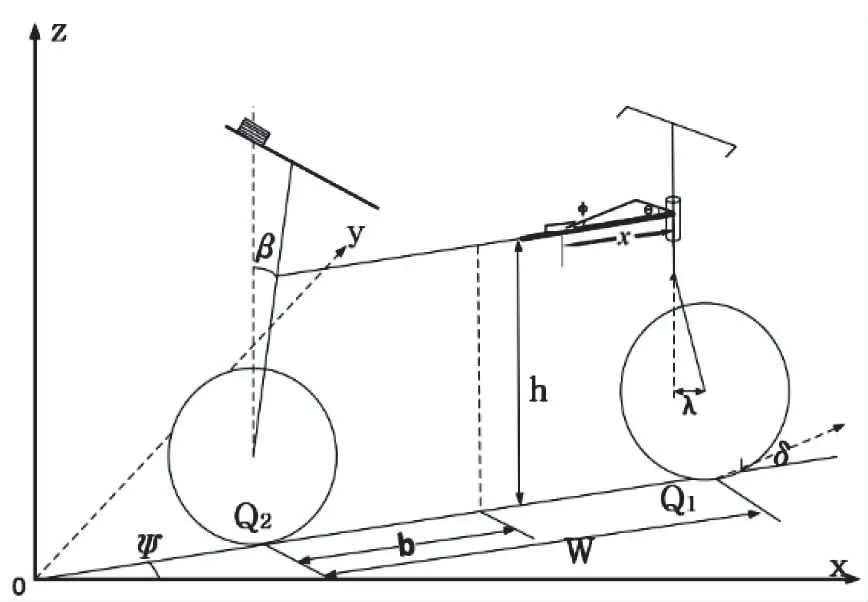
图1 无人驾驶自行车系统结构模型

图2所示为本文所用的无人驾驶自行车试验样机，遵循日常自行车前轮转向、后轮驱动的特性，由一辆常规自行车安装曲柄滑块机构装置、配重调节机构和电控系统等改造而来。其相关物理参数如表1所示。

表1 无人驾驶自行车的相关物理参数

2.2 曲柄滑块机构描述

2.2.1 曲柄滑块机构运动分析

记曲柄AB的长为c，连杆BC的长为a，滑块的位置相对A点的长为x，曲柄与滚珠丝杠滑台的夹角即曲柄转角为θ，连杆与滚珠丝杠滑台的夹角即摆角为φ；在对系统进行建模时，将曲柄看为车把的一部分，将连杆看为车架的一部分，忽略滑块的重量和其运动过程中所受到的摩擦力。

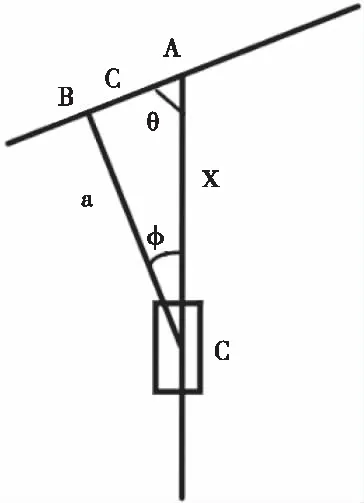
图3 曲柄滑块机构模型简图

由图3所示，利用三角关系，滑块位置x可表示为

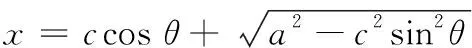
(1)

对模型进行近似化

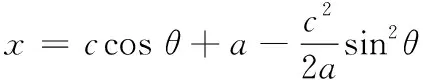
(2)

由图1可知，δ=90°-θ，代入式(2)得

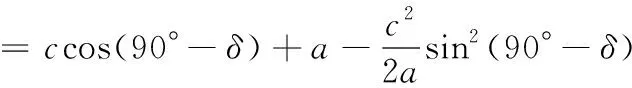
(3)

2.2.2 曲柄滑块机构受力分析

对于自行车转向系统的设计来说，传统的方法是直接将转向电机安装在前车把转轴上，而本文所设计曲柄滑块机构控制车体转向的方法，巧妙地运用了杠杆原理，相当于对力臂进行了延长，在转向电机输出同样力矩的情况下，前车把可以获得的力矩更大。如图4为滑块受力分析图。

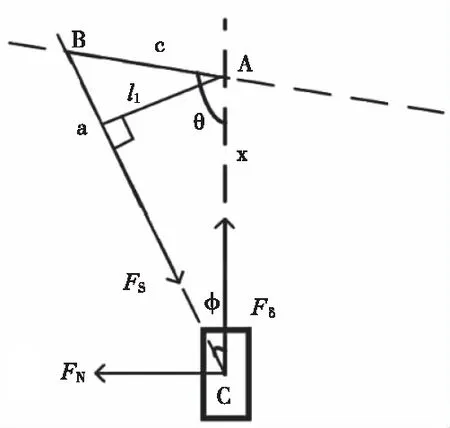
图4 滑块受力分析图

在图4中，Fδ为转向电机对滑块的输出推力，FN为滑台对滑块的挤压力，Fs为滑块作直线往复运动时连杆对滑块的推力，l1为转向过程中的力臂。由图4可知，根据力的分解及做功原理，Fδ和Fs的关系式可表示为

(4)

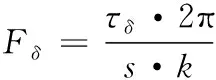
(5)

式中，τδ为转向电机输出力矩，s为滚珠丝杠螺距，k为同步增速比。

结合式(4)和式(5)可得：

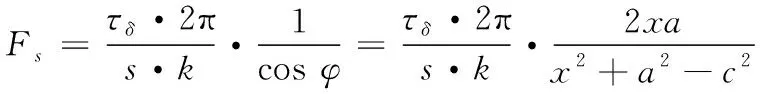
(6)

在ΔABC中，利用等面积法可得

(7)

将表1的实际参数值代入式(6)和式(7)，整理可得前车把转轴上受到的力矩τf为

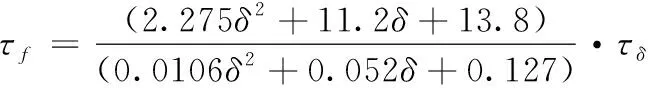
(8)

图5所示为力矩放大倍数与前车把转角关系的变化曲线。可以看出，曲柄滑块机构对转向电机输出力矩的放大倍数在56～144范围内。

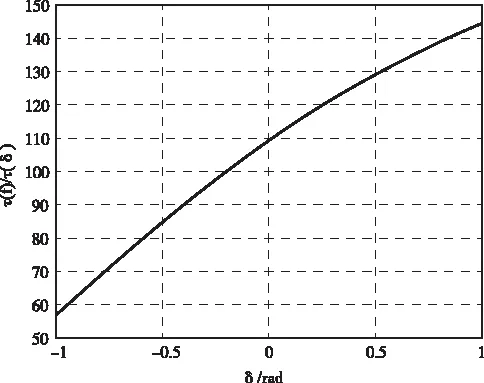
图5 力矩放大倍数与前车把转角变化曲线

2.3 拉格朗日方程法建立动力学模型

对图2所示的无人驾驶自行车，分为前车轮、后车轮、车架、前车把四个部分。并作如下合理化假设：前后轮质心均位于其圆心处；车把质心位于车把正中心，车架质心位于其质量中心，忽略曲柄滑块机构的质量。

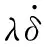
(9)

前轮动能为

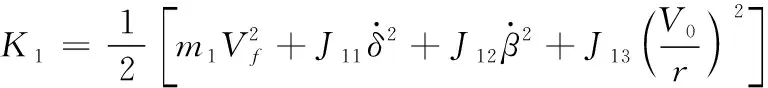
(10)

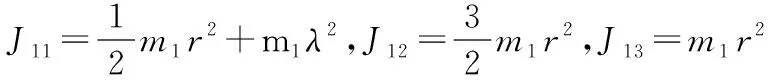
前轮势能为：

P1=m1grcosβ

(11)

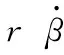
(12)

后轮动能为

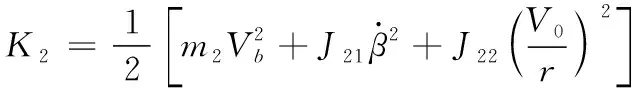
(13)

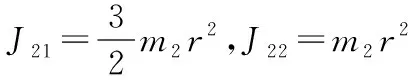
后轮势能为

P2=m2grcosβ

(14)

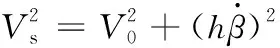
(15)

车架动能为

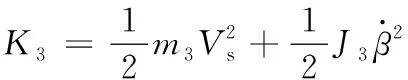
(16)

其中：J3=m3h2

车架势能为

P3=m3ghcosβ

(17)

(18)

车把动能为

(19)

车把势能为

P4=m4gh0cosβ

(20)

将上式进行相加，分别得系统总动能和总势能

K=K1+K2+K3+K4

P=P1+P2+P3+P4

(21)

根据第二类拉格朗日方程，代入Lagrange方程L=K-P

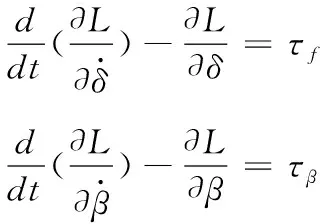
(22)

经整理可得，系统线性化动力学模型为

(23)

式中

3 滑模控制器设计

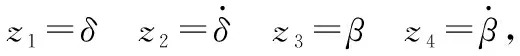
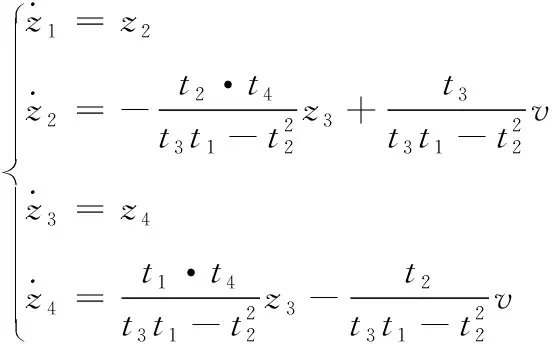
(24)

其中

t4=(m1gr+m2gr+m3gh+m4gh0)v=τf

首先进行误差方程的设计与分析，取

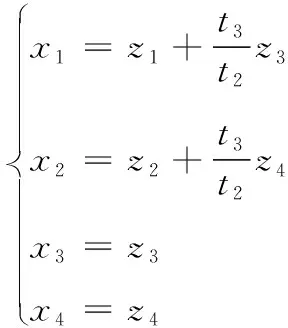
(25)

(26)

则有

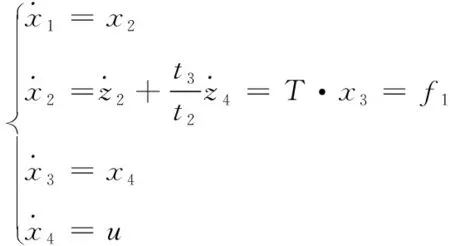
(27)

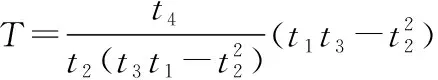
要使式(27)所示的系统稳定，f1需满足如下三个假设条件[8]：

假设1：f1(0，0，0)=0；

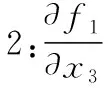
假设3：如果f1(0，0，x3)→0，则x3→0。

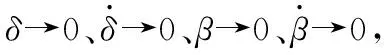
(28)

取滑模函数为

s=c1e1+c2e2+c3e3+e4

(29)

由式(29)可知

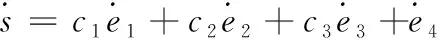
(30)

(31)

(32)

u=ueq+usw

(33)

4 仿真分析

图6 车体倾角变化曲线

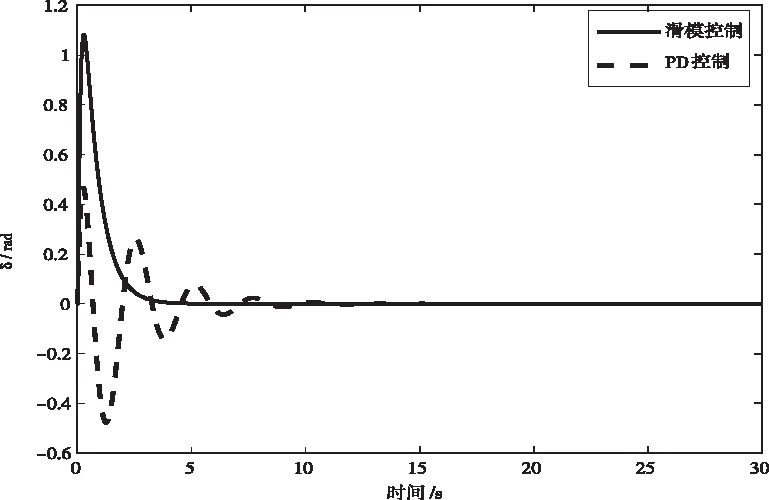
图7 前车把转角变化曲线

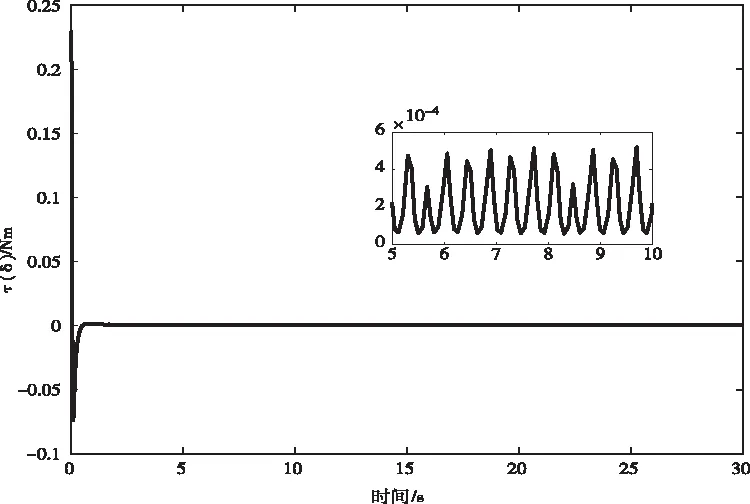
图8 转向电机输出力矩曲线

图9 前车把转轴力矩曲线

由图6和图7可知，系统起始处于向左倾斜0.03rad的不平衡状态，在控制器的作用下，前车把转角迅速向左转，在大约2s后，又迅速向右调节。对于PD控制器，大约10s后，车体倾角基本调节到平衡位置，前车把由于惯性作用，大约在13s后到达平衡位置；与PD控制器相比，滑模控制器所需的调节时间大大缩短，整个系统的调节过程大约只需3s，且曲线的整体变化趋势更加平稳。从图8和图9可以看出，在初始时刻，转向电机输出力矩急速增大，大约为0.24N.m，经曲柄滑块机构的放大，前车把转轴上获得的力矩为25N.m，在2s后，前车把转轴上的力矩保持在0到0.06N.m范围内维持一种动态调节状态。根据人的驾驶经验，当车体倾倒时，人总是本能的先将前车把向车体倾倒的一侧转动，等不再有继续倾斜的趋势后，再反向转动车把，使车体回到平衡位置，因此整个调节过程符合人们骑车的经验。