基于内聚力模型的纤维复合材料细观损伤模拟

纪怀旺，李增亮

(中国石油大学(华东)机电学院，山东 青岛 266580)

1 引言

纤维增强复合材料因比模量高、比强度高、密度小等诸多优势，在交通、建筑、航天等领域广泛应用[1]。碳纤维作为常用纤维，具有强度高、重量轻、导热快、耐疲劳的特点[2]；树脂产量大、强度高、耐热绝缘，是一种性能优异的非金属基体材料[3]。碳纤维/树脂综合了两种材料的优点，是一种有良好综合性能的复合材料，被誉为21世纪最具生命力成型材料。

细观力学是进行复合材料研究的一个重要手段。与宏观分析相比，细观分析不仅能简化模型、节省计算资源，还能更精确的描述材料的损伤机理。代表性体积单元(RVE)是复合材料细观尺度研究的重要工具[4]，其中几何模型生成与边界条件施加是两个重要环节，常由专业软件辅助完成，如Digimat、Fibersim等[5]。还有一种方法是有限元软件二次开发，该法不仅能充分发挥有限元软件的分析能力，而且灵活性更大。如文献[6]用随机序列吸附算法(RSA)生成了随机颗粒模型；文献[7]用背景网格对RSA进行改进，生成了不同直径、高填充率随机颗粒模型；基于ABAQUS开发的插件EasyPBC和Micromechanics Plugin能施加细观分析的复杂边界条件。

对RVE不同部分赋予不同的损伤属性，便能对复合材料的细观破坏行为进行分析。其中损伤属性主要包括：纤维损伤、界面损伤和基体损伤，由于纤维拉伸强度远大于界面和基体，所以在拉伸分析时常忽略纤维的损伤。文献[8]用内聚力单元对单纤维横向拉伸时的界面失效进行了研究，得到界面脱粘的变化规律；文献[9]基于多颗粒随机分布的炭黑/橡胶RVE研究了颗粒含量及团聚现象对界面损伤的影响；文献[10]分别使用内聚力单元和单元删除模拟界面损伤和基体损伤，研究了界面刚度、界面强度和界面断裂能的影响；文献[11]以砂/树脂单胞为研究对象，使用内聚力行为和扩展有限元(XFEM)分别模拟了界面损伤和粘结桥损伤。

综上所述，本文首先基于ABAQUS二次开发，通过编程实现了纤维复合材料细观模型的快速生成，提高了建模效率。然后基于更能反映真实受力情况的纤维随机分布的RVE，用内聚力模型(CZM)研究了界面损伤和基体损伤的破坏规律。其中，使用XFEM模拟基体损伤，由于该方法允许裂纹在网格中扩展，不需要像内聚力单元和单元删除一样通过精细的网格捕捉裂纹扩展路径，故能显著提高计算效率、节省计算时间。

2 RVE模型的建立

2.1 随机模型生成

一般纤维在取向处理后，在基体中可看作径向上均匀分布，并且与颗粒相比纤维长径比很大，短纤维长径比也在100～200间，故可将RVE简化为二维平面应变模型。

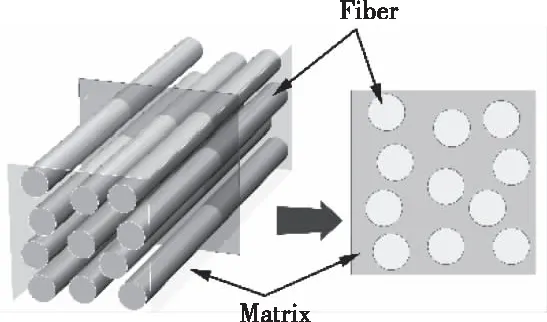
图1 随机纤维二维代表性体积单元

由RSA实现纤维随机分布可分为随机数生成、约束条件和绘制纤维三步。首先定义初始化参数(纤维直径d、纤维含量v和RVE边长与纤维长径比l/d)，然后利用Python中的random模块随机生成纤维圆心坐标。其中，坐标要满足约束条件：纤维在边界满足周期性分布；为避免网格扭曲过大，纤维间距和纤维与边界之间距离不能过小。

圆心坐标由程序循环生成，符合约束的存放到列表中，直到满足设定的纤维含量或达到最大无效生成次数后跳出循环。最后由绘图命令生成模型。

2.2 周期性边界

周期性边界条件(PBC)保证了分析部分与其在整体中分析时特性的一致，使分析结果准确可靠，因此应用广泛[12]。该条件使用时应满足变形协调和应力连续，其中应力连续在有限元法中自动满足[13]，故只需由位移约束满足变形协调。二维模型位移约束方程为

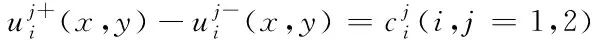
(1)

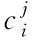
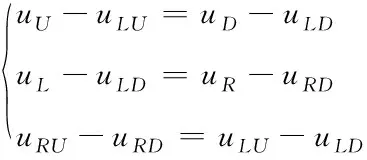
(2)

其中，uU、uD、uL、uR为矩形各边除角点外任一点的位移；uUL、uUR、uDL、uDR为各角点位移。此边界条件下，仅需在角点处施加位移载荷。软件中编程时由Equation语句通过约束对应边上的对应节点实现该边界条件。

3 内聚力模型

内聚力是物质中分子或原子之间的相互作用力，这种作用关系能有效描述材料损伤与破坏。CZM由牵引分离定律(TSL)进行表达，常见的TSL形式有双线性、线性、指数和梯形等[14]，如图2。

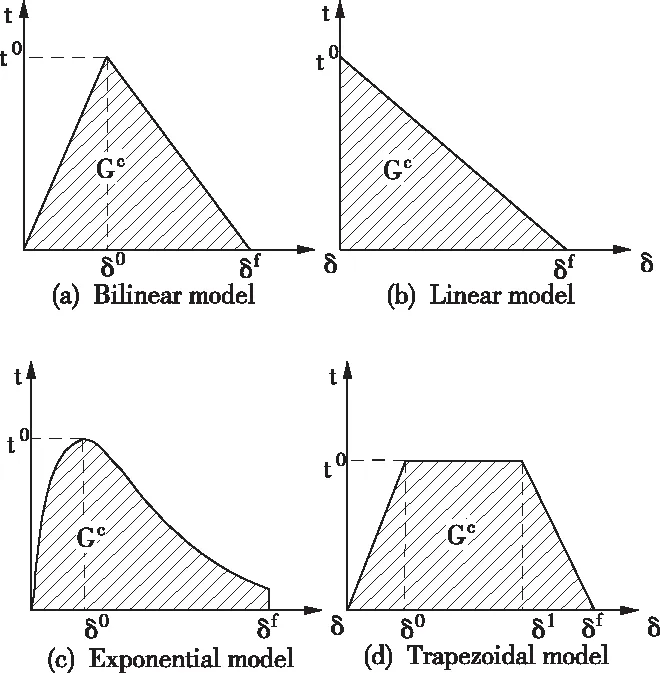
图2 不同形式的牵引分离定律

其中，t0为损伤起始应力；δ0为损伤起始位移；δ1为梯形模型实际损伤起始位移；δf为最大有效牵引位移；Gc为断裂韧度(值为阴影面积)。

TSL由无损伤阶段、损伤起始准则、损伤演化和失效准则构成，并可由内聚力单元和XFEM的实现。无损伤时，内聚力单元在不使用子程序时应力-应变仅能为线性，而XFEM此时由材料弹塑性本构控制，故其应力-应变曲线既能是线性，也能是非线性。

损伤起始准则由应力或应变表示，本文基体用最大主应力准则，界面用最大名义应力准则。损伤演化则由损伤因子D控制，其值在0～1间，0为无损伤，1为完全失效。演化方程[15]为

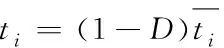
(3)

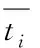
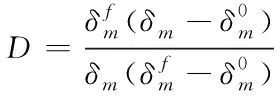
(4)

(5)

其中，δm为当前有效位移，G0为损伤演化前的断裂韧度。

失效准则与损伤演化对应，由位移或能量确定。其中位移法需给定δf，能量法需给定Gc。当破坏形式比较复杂时，还需要定义混合模式。对于能量法常用混合模式有BK准则、Powerlaw准则等。其中，BK准则应用广泛、简单可靠，其表达式为：

(6)

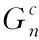
4 扩展有限元

材料的不连续行为包括强不连续和弱不连续[16]。其中，强不连续指位移场不连续，如裂纹；弱不连续指应变场不连续，如夹杂、孔洞。

4.1 单位分解法

单位分解法(PUM)是XFEM的重要理论基础，该方法实现了由局部精确近似达到整体精确近似。由PUM得对任意给定函数ψ(x)，在其求解域内都可表示为：

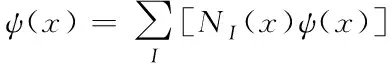
(7)

其中，I为求解域中交叉子域ΩI的编号；NI(x)为子域形函数，仅在对应子域内非零，且在整个求解域内满足单位分解条件

(8)

4.2 水平集法

水平集法(LSM)是用于判断界面位置和追踪界面移动的数值技术。该方法由水平集函数实现，不连续界面通过零水平集表示，界面两端的水平集函数符号相反。对于任意一个裂纹Γc(t)⊂R2由两个水平集函数才能准确进行追踪定位：

Γc(t)={x∈R2：φ(x，t)=0andγ(x，t)≤0}

(9)

其中，φ(x，t)为裂纹水平集函数；γ(x，t)为波前函数。裂纹的LSM具体表示方法如图3。

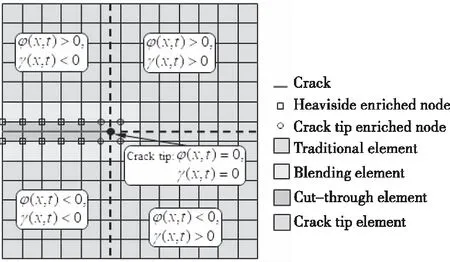
图3 裂纹的水平集函数表示方法

4.2 扩充函数构造

基于PUM和LSM，对传统有限元形函数扩充得到扩充形函数，从而得XFEM的位移逼近方程一般形式

u(x)=ucon+udis

(10)

其中，ucon为连续部分位移场；udis为不连续部分位移场，两者表达式分别为

(11)

(12)

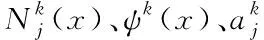
(13)

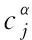
5 数值模拟及分析

5.1 数值模型建立

为提高计算效率并保证模型精确性，l/d取4，d取0.02mm，生成纤维含量为29.5%的RVE。划分网格时，基体和纤维采用CPE4单元，界面插入零厚度COH2D4单元。单元划分完后为其赋予材料属性，其中基体为环氧树脂，拉伸破坏时为近似脆性[18]。因此，无损伤阶段采用线弹性本构，损伤起始后采用图2(b)的线性模型。基体材料参数见表1：

表1 环氧树脂基体的材料参数[11]

纤维作为增强相，模量和强度远高于基体，对整体性能起到重要影响作用。本文采用纤维材料为T300，分析时作为线弹性材料，其弹性模量为13.8GPa、泊松比为0.2[19]。界面强度是一个重要指标，本文在仅界面损伤和界面、基体同时损伤两种条件下，通过改变界面强度大小分析其对材料性能的影响。其中，法向强度取树脂基体强度的60%，80%，100%，切向强度取法向强度1.5倍，其余参数见表2。

表2 粘结界面材料参数[20]

赋予材料后施加PBC，再添加位移载荷：

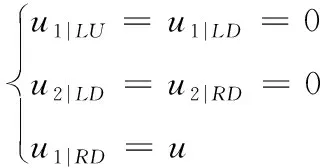
(14)

其中，u为位移载荷。图4为最终模型。

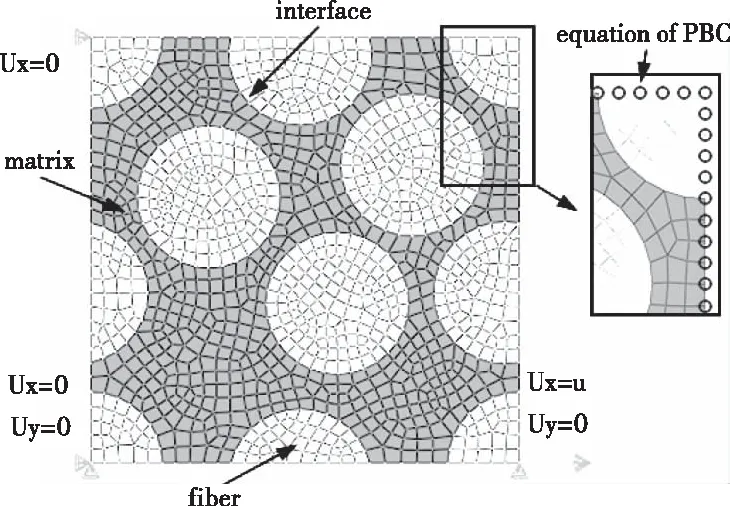
图4 数值模型

5.2 界面损伤

仅界面损伤时，受到横向拉伸载荷后，界面法线方向与位移载荷方向所夹锐角最小处最先失效，随位移载荷增加，失效界面逐渐向垂直于位移载荷法线方向扩展。界面将基体与纤维粘合，当复合材料发生变形时，力由基体通过界面作用在纤维上，因此界面有传递力的作用。相同载荷条件下，传递到纤维的作用力越大，表明纤维承受载荷越高，对基体增强效果就越好。因此，纤维的应力变化能准确反映界面损伤的变化情况。图5为仅有界面失效时纤维横向平均应力-位移曲线，可得界面强度为60%的最大平均应力为15MPa，80%时为19MPa，100%时为23MPa。

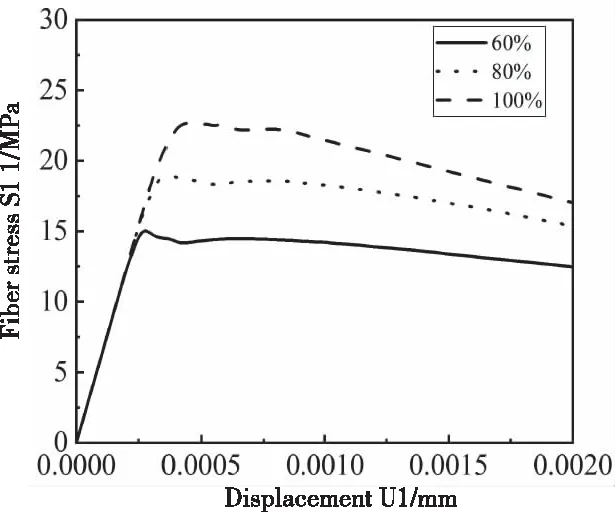
图5 不同界面强度下纤维平均应力

5.3 界面/基体损伤

考虑基体损伤时，XFEM可以捕捉到基体中的裂纹萌生、扩展如图6，以及基体破坏与界面的相互作用，如图7中的a处为基体裂纹引起的界面损伤。

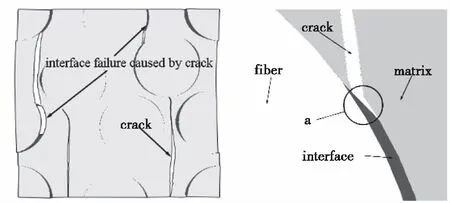
图6 界面/基体损伤 图7 裂纹引起界面损伤

可得，基体中裂纹遇到纤维后引起界面损伤，这种“损伤转移”将基体裂纹转换为界面损伤，从而有效抑制了裂纹在基体中的“生长”。

图8 相同位移不同界面强度下基体平均应力

图8为不同界面强度时两种不同条件下树脂基体平均应力，仅考虑界面损伤时基体平均应力分别为13.6MPa、15.8MPa和18.1MPa，而同时考虑基体损伤时平均应力为13.1MPa、14.6MPa和15.7MPa。对比发现，无论何种损伤行为树脂基体平均应力与界面强度均为正比关系，而同时考虑界面和基体损伤时，基体平均应力明显下降，并且随着界面强度的增加平均应力差值明显扩大。为表明基体损伤对RVE整体性能的影响，图9、图10分别给出界面损伤和界面/基体损伤时RVE平均应力变化曲线：

图9 界面损伤

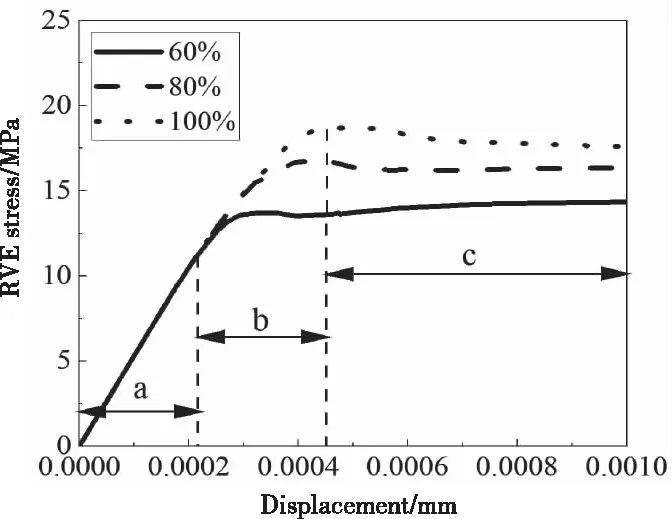
图10 界面/基体损伤

RVE的应力-位移曲线可分为a-b-c三阶段。a位于小范围位移载荷内，此时模型平均应力与位移载荷呈线性增大关系。当位移载荷超过某值(约为0.00022mm)后到达b阶段，此时界面损伤起主要作用，不同界面强度的应力曲线开始出现分支，且界面强度越大应力值越高。当位移载荷增加到约0.00042mm时应力曲线到达c阶段，此时无基体损伤应力曲线呈现缓满上升趋势，而有基体损伤的应力曲线在呈缓慢下降趋势，由于两者仅基体损伤这一变量不同，所以可得下降是由基体损伤引起的。

6 结论

1)结合RSA和PBC，由二次开发实现纤维复合材料快速建模，极大简化建模流程。

2)仅考虑界面损伤时，纤维平均应力表明界面强度越大，受横向拉伸时纤维所受力就越大，纤维增强效果就越好。因此界面强度对纤维增强作用的发挥具有重要意义。

3)考虑界面/基体损伤时，XFEM准确捕捉到基体裂纹：萌生于位移载荷方向上相邻较近的纤维之间；扩展方向与位移载荷方向垂直；裂纹由于引发界面损伤而停止扩展，且界面强度越大对裂纹的抑制作用越好。

4)横向拉伸时，仅有界面损伤的RVE平均应力呈先快速上升后缓慢上升的趋势，而考虑界面/基体损伤的RVE平均应力为先快速上升后缓慢下的降趋势。表明当位移载荷超过某临界值后仅使用界面损伤模型是不准确的。这对纤维复合材料实际破坏行为的研究具有重要指导意义。