城轨供电系统杂散电流对埋地金属管道的动态干扰研究

黄晓鹏 ，马庆安，刘炜，尹乙臣，周林杰

(1. 西南交通大学 电气工程学院，四川 成都 610031；2. 西南交通大学 唐山研究生院，河北 唐山 063000)

采用走行轨回流的直流牵引供电系统存在轨道电位与杂散电流问题[1]。为防治杂散电流，工程设计中，多采取避让的方式选择地铁线路路径或管道路径。地铁近年来发展极为迅速。随着我国对能源需求的快速增长，油气管道的建设也在迅速增加[2-3]，经常会出现地铁线路和埋地金属管道接近或交错的情况。因此，研究直流供电系统杂散电流对金属管道的干扰影响具有现实意义。蔡力等[4]对地铁杂散电流对钢轨的腐蚀进行了分析，得到杂散电流与过渡电阻和机车位置的关系，为工程设计提供了参考。LIU 等[5]介绍了杂散电流收集网在杂散电流防护中的作用，并根据电流源和传播路径，将杂散电流区分为一次和二次杂散电流。朱峰等[6]通过建立地铁回流系统到大地的电路模型，分析了不同轨地过渡电阻和轨地过渡电阻不均匀对杂散电流的影响。白锋等[7]利用函数拟合的方法得到高压直流接地极杂散电流与管道金属腐蚀量的关系，该方法需要有充足的数据样本，对应用目标有一定要求。董亮等[8]基于数值模拟方法，对几种特定情况下的地铁杂散电流对管道干扰的影响进行了计算与分析，并选取其中的部分情形设计了相应的缓解方法。周兰等[9]讨论了杂散电流防护的必要性，并提出一种新的管道联合保护方案。目前，对于直流牵引供电系统杂散电流的泄漏有较多研究，但杂散电流对管道的动态干扰仍有一定的研究空间。本文建立直流牵引供电系统和埋地金属管道的联合计算模型，利用分层介质模型计算由地铁线路在大地中产生的电位分布，基于矩量法建立埋地金属管道电路模型，并进行仿真计算。利用接地分析软件CDEGS 对综合计算模型进行验证。使用该模型分析国内某地铁线路杂散电流对附近埋地金属管道的影响，并与实测数据进行对比。

1 模型的建立

1.1 回流系统杂散电流动态分布

直流牵引供电系统的杂散电流传播和扩散的路径包括钢轨、杂散电流收集网、大地和管道等，如图1所示。

图1 直流牵引供电系统杂散电流扩散示意图Fig. 1 Schematic diagram of stray current diffusion in DC traction power supply system

忽略金属管道对钢轨泄露的杂散电流幅值的影响，基于线路参数以及列车、变电所工作状态，建立牵引供电系统的电路模型，通过潮流计算，可获得全线钢轨电位和杂散电流动态分布情况，具体计算过程见文献[10]-[12]。

地铁各车站安装有钢轨电位限制器，钢轨经钢轨电位限制器悬浮接地，而车辆段存在直接接地和采用钢轨电位限制器悬浮接地2种形式。当钢轨经钢轨电位限制器接地时，钢轨电位限制器可分为合闸和分闸2 种状态，t时刻钢轨电位限制器处钢轨对地电阻为：

式中：RO为钢轨电位限制器分闸时的钢轨对地电阻；RI为钢轨电位限制器合闸时的钢轨对地电阻；S(t)为t时刻钢轨电位限制器的状态；S0表示钢轨电位限制器处于分闸状态；S1表示钢轨电位限制器处于合闸状态。

车辆段钢轨对地电阻为：

式中：Rdg为钢轨直接接地电阻；P为车辆段接地方式；P0为直接接地；P1为通过钢轨电位限制器接地[13]。

1.2 分层介质模型

地铁杂散电流在水平分层介质中的扩散模型第1 层介质为混凝土层，钢轨置于混凝土层表面，杂散电流收集网在混凝土层；第2层介质为土壤[6]。

第1.1 节中已得到钢轨杂散电流分布。将每小段钢轨泄露的杂散电流视作点电流源，计算各点电流源在分层介质中产生的电位分布，基于叠加原理，可得到杂散电流在介质中任意位置产生的电位分布。

杂散电流在混凝土中产生的电位为：

式中：r=为电流源位置；(x＇,y＇,z＇)为介质中电位位置；ρ1为第1 层介质(混凝土)电阻率(Ω·m)；i为点电流源泄漏电流；J0为第1 类零阶贝塞尔系数；α1和β1为待定系数。

杂散电流在土壤中某点产生的电位为：

式中：ρ2为第2层介质(土壤)电阻率，Ω·m；α2和β2为待定系数。

解式(3)和式(4)求得待定系数，利用Prony 法可以求得土壤层中任意位置的地电位：

其中，s0，s＇0，sn1，sn2，sn3和sn4分别为：

式中：an和bn为待定系数；h1为混凝土厚度，m；h0为电流源埋地深度，m。

1.3 基于矩量法的管道电路模型

对埋地管道进行分析，将整条管道划分为许多小段，如图2 所示。基于矩量法原理，在管道内，只有沿轴线方向传导的电流；在管道与大地之间，存在由大地流入各段管道的电流。

图2 埋地管道分段Fig. 2 Buried Pipeline Segmentation

对于某段管道，Iin为前一段管道流入该段的轴向电流，Iout为该段管道流入下一段的轴向电流，Iin和Iout由杂散电流作用下管道上的电压降决定。Id为由大地流入该段管道的电流，其幅值取决于杂散电流。

管道平均划分为n段时的管道电路模型如图3所示。图中，Ik为由大地流入第k段管道的电流，A；Ur,k为杂散电流在第k段管道中点防腐层外产生的电位，V；Ug,k为各段管道的漏电流在第k段管道中点防腐层外产生的电位，V；Up,k为第k段管道中点的电位，V；Zg,k为第k段管道的防腐层电阻，Ω；Zp,k为第k段管道纵向电阻，Ω/km。

图3 埋地管道等效电路Fig. 3 Buried pipeline equivalent circuit

管道防腐层外表面的电位由杂散电流在此处产生的电位和管道自身泄漏电流在此处产生的电位2 个部分组成。各段管道的泄漏电流在第k段管道中点防腐层外产生的电位为：

Zeij为第i段管道的单位漏电流在第j段管道防腐层外中点产生的电位[3]。由大地注入各段管道的电流为：

各段管道的中点电位为：

其中，直流牵引供电系统杂散电流在防腐层外产生电位为：

管道防腐层电阻为：

每段管道的防腐层电阻为：

式中：ZA为管道防腐层面电阻，Ω·m2；r为管道半径，m；l为基于矩量法对管道分段后每段管道的长度，m。

由基尔霍夫定律，可得式(15)：

式中：Y为根据埋地金属管道模型建立的节点导纳矩阵，具体表达式为：

由式(7)，式(11)和式(15)可得线性方程组(17)：

式中：E为n阶单位矩阵。

解线性方程组(17)可得到管地电位Up。

杂散电流对管道全线干扰情况的评估如图4所示。

图4 杂散电流对管道干扰计算Fig. 4 Calculation of stray current interference on pipeline

2 模型验证

为验证模型正确性，使用CDEGS 软件MALZ模块构建全长9 000 m 的双边供电线路模型，如图5 所示。全线设置4 座牵引变电所，6 列列车，将钢轨、杂散电流收集网和管道分别等效成一根长导体，将牵引变电所和列车各等效为电流源，分析水平距离线路100 m 远处，未使用阴极保护的管道的电位分布情况。

图5 CDEGS仿真示意图Fig. 5 CDEGS simulation diagram

4 座牵引变电所分别位于0，3，6 和9 km 处，列车A～F 分别位于0.5，2，3.5，5，6.5 和8 km处，列车牵引电流均为3 000 A。埋地金属管道长2 500 m，直径0.5 m，与3 500～6 000 m 区段内的线路平行，垂直距离5 m(在线路下方)，水平距离100 m。

钢轨、杂散电流收集网和埋地金属管道的纵向电阻分别为0.018，0.15 和0.2 Ω/km，钢轨涂层电阻为1 000 Ω·m2，杂散电流收集网涂层电阻为100 Ω·m2。钢轨对杂散电流收集网和杂散电流收集网对地的过渡电阻分别为1.499 7 Ω·km 和0.490 2 Ω·km 。管道防腐层采用3PE 材料，面电阻为105Ω·m2[15]。金属材料在一般土壤环境中的自然电位ECOR参考值为-0.65～-0.40 V[16]，本文中的模型为在一般土壤和水环境中、管道无保护条件下的系统模型，因此管道自然电位取ECOR=-0.65 V。

假设模型中管道为新建管道，破损率取0.003%[15]。此时，管道全线电位如图6 所示。可见，计算方法和仿真方法得到的管地电位相近，误差不超过4.11%，故所提计算方法可用于管地电位计算。

图6 防腐层破损时的管地电位分布Fig. 6 Pipe-ground potential distribution when the anti-corrosion coating is damaged

3 案例分析

国内某地铁及其附近的埋地金属管道的走向如图7所示。本案例中管道附近仅有一条地铁线路产生直流干扰。

该地铁线路采用DC1500V 刚性悬挂的架空接触网授流、走行轨回流的牵引制式。列车采用6辆编组B型车，最高速度100 km/h。线路全长21.57 km，共13 个站点，10 个牵引变电所。管道全长13 km，管径为377 mm，防腐层为3PE 材料。管道使用年数在10 a 以内，根据经验值防腐层破损率取0.04%[15]。管道设有5 个测量点P1～P5，如图7 所示。采用断电法对管道进行连续测量，测得测量点处24 h的管地电位。

图7 线路与管道位置示意图Fig. 7 Schematic diagram of metro line and pipeline location

同时也测量了地铁线路钢轨对杂散电流收集网过渡电阻等参数，地铁及管道参数如表1。发车间隔为300 s，最大制动电压为1 800 V。

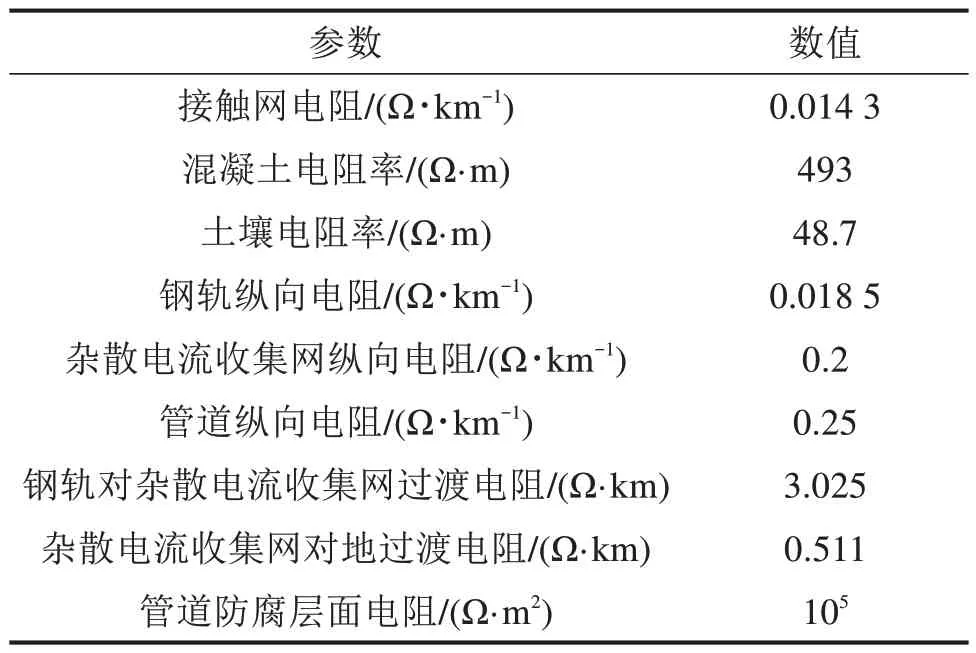
表1 地铁及管道参数Table 1 Metro and pipeline parameters

以S1 为起始点，全线钢轨电位随时间变化情况如图8所示。

图8 钢轨电位动态分布Fig. 8 Dynamic distribution of rail potential

以A为位置起始点的管地电位随时间变化情况如图9所示。由图9可知管道全线在该时段内最高管地电位为329.6 mV，最低管地电位为-253.9 mV。

图9 管地电位动态分布Fig. 9 Dynamic distribution of pipe-ground potential

管道的动态电位波动值如图10 所示，仿真结果与各测量点实测值误差在8.21%以内。误差来自于地铁全线钢轨纵向电阻、过渡电阻并不均匀，以及管道破损情况是根据管道年限基于经验值取得，与实际破损情况也存在差异等因素。从图10可见，埋地管道全线管电位波动值均超过350 mV，全线管道受到杂散电流强烈的干扰腐蚀[17]。其中管道首端(A 端)管电位波动值最大，为583.6 mV；管道末端(B端)管电位波动值最小，为351.3 mV。

图10 管地电位波动值Fig. 10 Pipe-ground potential fluctuation value

由图10 可知，0～4.2 km 区段的管地电位波动呈现迅速降低趋势，该段为由西向东走向和由南向北走向，地铁线路在管道西侧及南侧，该段管道逐渐远离地铁线路，造成管地电位波动减小。4.2～7.8 km 区段的管地电位波动变化较小，该段管道为东南-西北走向，一方面地铁线路大部分区段位于该段管道西南侧，随管道逐渐向北，与地铁线路距离逐渐增大；另一方面，随管道逐渐向西，与地铁线路末段距离减小，且逐渐靠近地铁车辆段，而地铁车辆段杂散电流泄漏较多，两方面因素共同作用，使得该段管道波动变化较平缓。7.8～13 km 管道的管地电位呈现波动迅速降低趋势，该段管道为由南向北走向，地铁线路在该段管道西南侧，该段管道逐渐远离地铁线路以及地铁车辆段，造成管地电位波动减小。

本案例中，仅对线路附近的土壤情况进行了勘测。但区域的地质和地形并非均匀分布，因此也会对结果造成一定的误差，且距离线路越远，造成的误差越大。

4 杂散电流对管地电位影响规律分析

以第3节案例为例，研究杂散电流对管地电位的影响规律。

当最大波动值满足管道杂散电流防护要求时，则说明管道全线满足杂散电流防护要求。管道全线防腐层不同破损率情况下的管道全线电位最大波动值，如图11 所示。由图11 可知，随着管道防腐层破损率的降低，管道全线电位最大波动值也随之减小，即通过改善管道防腐层保护效果可以降低杂散电流对管道的干扰腐蚀危害。当管道防腐层破损率从0.5%降至0.001%时，管地电位最大波动值由595.9 mV 降至440.7 mV， 下降了26.04%。

图11 不同防腐层破损率管地电位最大波动值Fig. 11 Maximum fluctuation value of pipe-ground potential of different anti-corrosion coating damage rates

不同钢轨对杂散电流收集网过渡电阻情况下的管地电位波动值如图12 所示。可知，增大钢轨对杂散电流收集网过渡电阻可以减小杂散电流对管道干扰腐蚀危害。根据标准CJJ/T 49—2020，钢轨过渡电阻值不应小于15 Ω·km，当全线钢轨过渡电阻由1 Ω·km 增大至15 Ω·km 时，管地电位最大波动值由1 220 mV 降低至214.2 mV，下降了82.44%，杂散电流对管道干扰腐蚀危害程度由强烈降为中等[17]。

图12 不同过渡电阻管地电位最大波动值Fig. 12 Maximum fluctuation value of the pipe-ground potential of different transition resistances

当线路分别采用120，240 和360 s 发车间隔时，管道1 km 处的管地电位如图13 所示。发车间隔为240 s和360 s时管地电位平均偏移量分别比发车间隔120 s下降了27.45%和43.27%，发车间隔较短时杂散电流对管道干扰情况更加严重。

图13 不同发车间隔管地电位Fig. 13 Pipe-ground potential of different departure intervals

当车辆段分别采用钢轨电位限制器悬浮接地和直接接地时，管道1 km 位置处的管地电位如图14 所示。在钢轨电位限制器悬浮接地情况下，管地电位平均偏移量比直接接地下降了11.91%，直接接地方式会使管道受杂散电流干扰更加严重。

图14 不同接地方式下的管地电位Fig. 14 Pipe-ground potential of different grounding methods

5 结论

1) CDEGS 的仿真结果和现场实测结果表明了本文研究的有效性。

2) 增大钢轨对杂散电流收集网过渡电阻比其他方式更有利于降低直流牵引供电系统杂散电流对金属管道的干扰。将管道全线防腐层破损率由0.5%降低至0.001%，管地电位最大波动值降低了26.04%。将全线钢轨对杂散电流收集网过渡电阻由1 Ω·km 增大至15 Ω·km，管地电位最大波动值下降了82.44%。发车间隔360 s 时的管地电位偏移量比发车间隔120 s 时下降了43.27%。车辆段经钢轨电位限制器接地时的管地电位偏移量比直接接地下降了11.91%。