“站桥合一”高架车站动力响应影响参数研究
2023-03-29郭向荣刘江浩吴业飞蒋晔
郭向荣,刘江浩,吴业飞,蒋晔
(1. 中南大学 土木工程学院,湖南 长沙 410075;2. 中铁第四勘察设计院集团有限公司,湖北 武汉 430063)
为缓解大城市核心区人口密集、交通拥堵、环境恶化等问题,越来越多的城市群之间开始新建高架轨道交通工程。高架车站作为此类工程的主要附属设施具有投资少、建设周期短、对道路交通干扰小、工程建设难度低等优点,近年来在市域轨道交通和城际铁路工程中得到大量应用[1]。“站桥合一”型结构作为高架车站主要的结构形式之一,因其具有整体刚度好,结构体系柱网简单,能有效降低车站整体高度等优点逐渐成为当前的主流站型。然而,相较于其他结构形式,“站桥合一”型高架车站融合了车站建筑和桥梁2种不同受力体系的结构特性,结构刚度及质量分布在水平和竖直方向都有很大的不均匀性,因此在结构设计阶段,存在着不同结构体系之间传力路径复杂、车致振动引发的结构动力耦合作用难以明晰、现有的设计规范不能统一等一系列问题[2-3]。为此,国内外展开了一系列的研究,并取得了一些研究成果。数值模拟方面,邓世海等[4-5]将列车-桥梁动力相互作用计算得到的桥梁轨道上各节点荷载时程作为外部激励施加到桥梁-站房结构上进行时程分析,对列车匀速通过车站时的结构动力响应进行了计算并对车辆与结构的安全性与舒适性做出了评价。冉汶民等[6]采用频域分析方法计算站房结构振动响应,探讨了轨道扣件刚度对站房振动的影响,得到了站台层和站房的振动响应规律。ZHU 等[7-9]建立列车—轨道—站房耦合系统整体动力学模型,对车辆荷载作用下车站各楼层的随机振动特性展开了分析,探究了车致车站随机振动随车速变化的规律以及车致振动沿车站水平方向和高度方向的传播衰减规律。现场实测方面,谢伟平等[10]对列车到发站时站房结构振动和结构噪声响应进行现场测试,分析了地铁高架车站的振动和结构噪声响应规律,并基于测试结果对不同功能区进行了舒适度评价。巴振宁等[11]通过现场实测,对不同车速造成结构振动、不同测点振动以及两车交会行驶时产生的振动进行了对比分析,为“站桥合一”结构形式高铁站的模拟预测提供了依据。上述研究多是从车致车站振动响应的分布、传播、衰减规律和车致振动对车站结构的安全性、舒适性以及使用性能的影响等方面进行展开[12-14],分析车站结构尺寸本身对其动力响应影响的研究还比较少。为解决上述问题,本文选取某典型“站桥合一”型高架车站为研究对象,采用中南大学郭向荣教授自编软件,以弹性系统动力学总势能不变值原理和“对号入座”法则为基本准则,将列车、轨道和车站结构视为一个整体,结合能量法建立列车-轨道-车站空间耦合振动方程,以此建立具有不同高度轨道梁,不同楼板厚度,不同截面尺寸框架柱的计算模型,采用时域分析方法求解。分析多种结构参数对车站的动力响应的影响,以期为“站桥合一”型车站结构设计提供参考。
1 工程概况
“站桥合一”型车站结构示意图见图1。车站设计速度为120 km/h,设4 线客运专线,中间两线为越行线。站房采用全现浇空间框架结构体系,站房主体由下到上为站厅层、承轨层、站台层;车站总高度约21~22 m,层高自下而上距离地面分别为7.65,13.30和14.90 m。车站总长度120 m,总宽度为31.80 m,横向布置3 排柱,柱间距10.5 m+10.5 m,柱外侧悬挑5.4 m。纵向柱网布置为10 跨12 m,不设变形缝,车站端部横梁与桥梁结构共用墩柱,均采用简支支座支撑在桥墩上。

图1 车站结构示意图Fig. 1 Schematic diagram of station structure
2 列车-轨道-车站耦合系统分析模型
2.1 列车仿真分析模型
在对列车空间模型进行模拟时,通常需要根据车辆的构造特点进行必要的简化,以便在保证车辆模型的精确性的情况下提高计算效率。参照文献[13]建立车辆模型,车体和每个构架有点头、侧摆、侧滚、沉浮、摇头5个自由度;每个轮对有侧摆、摇头2 个自由度,所以每辆4 轴车辆共有23个自由度。列车在桥梁上行驶时,列车在桥梁上的位置是不断变化的,首先计算出一节车的总势能Πv,再运用势能驻值原理δΠv=0 以及形成矩阵的“对号入座”法则可得出车辆的运行方程:
式中:[Mv],[Cv],[Kv],{Pv}分别为单节车辆的质量、阻尼、刚度矩阵和荷载列阵,{δv}分别为相对应的位移、速度、加速度参数列阵。
2.2 轨道-车站仿真分析模型
在建立轨道-车站结构有限元分析模型时,站房结构的梁、柱、轨道梁和雨棚梁、雨棚柱、雨棚斜撑均采用空间梁单元建模,站房结构中的楼板则采用板壳单元建模,所有材料均假设为线弹性,弹性模量E和泊松比均按照规范取值,主要构件材料强度见表1。

表1 车站构件材料强度等级Table 1 Material strength classes for station components
采用瑞利阻尼模拟站房结构的阻尼,阻尼比取2%,结构桩基础则运用m 法考虑桩土共同作用建模。本文建立的“站桥合一”车站结构有限元模型如图2所示,共有5 149个节点,由5 077个梁单元和4 152个板单元组成。

图2 车站有限元模型Fig. 2 Finite element model of station
2.3 列车-轨道-车站耦合振动方程的建立及求解
本文把列车-轨道-车站(以下简称车轨站)视为一个耦合时变整体系统,以各单体结构静力平衡位置为坐标原点,将车站结构的边界条件作为此系统的边界条件,轮轨间复杂的接触就变成了系统内部的接触,这样可以排除不确定性,确保方程有唯一解[15]。考虑各车辆与车站空间振动位移的相互关系,计算出车轨站系统在任意时刻t的总势能Πd(t),包括车辆的总势能Πv(t)和轨道-车站的总势能Πb(t),然后运用弹性系统动力学总势能不变值原理δΠd(t) =0 和形成矩阵的“对号入座”法则,可以建立t时刻车轨站系统的振动方程:
式中:[M],[C],[K]分别为车轨站系统在t时刻的质量、阻尼、刚度矩阵;分别为车轨站系统在t时刻的加速度、速度、位移列阵;{P}为车轨站系统在t时刻所受由轨面不平顺(含动态或静态)所导致的轮轨接触力以及车辆自重组成的荷载列阵。
考虑到车轨站系统振动方程中,各系数矩阵将随弹簧特性和阻尼特性的改变而改变。故该变系数线性方程无法采用振型叠加法进行求解,目前最合适的办法是采用逐步积分法。本文采用一种精度较高、高效而独特的显式型显-隐式混合积分法:对系统动力学方程中各矩阵对角元部分采用内插线性加速度隐式积分格式,而对各矩阵中非对角元部分采用外延线性加速度显式积分格式,将二者进行混合求解,大大提高了积分精度和求解效率。
3 不同车速工况下车站结构动力响应分析及模型空间耦合振动计算结果验证
3.1 车站结构动力特性分析
采用前面建立的轨道-车站有限元模型,通过模态分析得到了结构前100 阶振型。其中首阶横弯、竖弯、纵飘自振频率及振型特点如表2 所示,绘出的各首阶振型图见图3~6。

表2 车站模型自振频率Table 2 Natural vibration frequency of station model

图3 结构第1阶振型图(轴视图)Fig. 3 1st vibration mode(Axis view)

图4 结构第2阶振型图(正视图)Fig. 4 2st vibration mode (Front view)

图5 结构第11阶振型图(正视图)Fig. 5 11st vibration mode (Front view)

图6 结构第48阶振型图(正视图)Fig. 6 48st vibration mode (Front view)
3.2 不同车速工况下车站动力响应结果及分析
根据前述计算原理与车轨站模型,采用自编软件建立车轨站结构动力耦合分析模型。进行车轨站耦合计算时,选用B型列车,车辆编组为(动+拖+拖+拖+拖+动),采用美国六级谱生成的轨道不平顺样本模拟行车过程中的附加轨道不平顺,计算单线满载列车以80~120 km/h 车速沿下行方向越行通过车站时车站结构的动力响应。5 种不同车速工况下单线列车越行通过车站时站厅层楼板与站台层楼板的横向、竖向、纵向位移与加速度如表3 所示,表3 中振动位移值均为相对于初始平衡位置而言。为了更直观地看出站台层与站厅层楼板响应受列车车速的影响,各响应指标的曲线图如图7所示。

表3 不同车速工况下车站结构动力响应最大值Table 3 Maximum dynamic response of station structure under different speed conditions

图7 不同车速工况下车站站台层与站厅层动力响应最大值Fig. 7 Maximum dynamic response of station platform floor and station hall floor under different speed conditions
当单线满载B 型列车以80~120 km/h 速度匀速通过“站桥合一”车站时,站台层楼板、站厅层楼板的竖向加速度响应均明显大于横向和纵向加速度响应。随着行车速度的增大,站厅层楼板和站台层楼板的最大横向、纵向位移随着车速的增大均呈先增大后减小的趋势,站厅层竖向位移则呈现增大趋势,站台层竖向位移则基本保持不变。站厅层楼板和站台层楼板的最大竖向加速度随车速增加均呈增大的趋势,站台层楼板的横向、纵向加速度基本保持不变,而站厅层楼板的横向、纵向加速度则呈增大趋势。
3.3 行车动力响应结果对比验证
大量研究表明车站结构振动响应主要受列车竖向动力荷载控制,车致车站振动以竖向振动为主[7],为验证数值模拟的可靠性,取站厅层、站台层楼板处的竖向加速度时程进行对比分析,实测工况为6节空载编组沿下行方向越行通过车站,车速在100 km/h 左右。各测点纵向布置如图1 所示,横向布置如图8 所示,测点1 号与测点2 号为站厅层测点,距离结构断面中心线分别为0.838 m,5.838 m,测点3号与测点4号为站台层测点,距结构断面中心线分别为13.265 m,15.765 m。计算工况取6节空载编组沿下行方向越行通过车站,车速为110 km/h。各层楼板测点的实测与计算竖向加速度时程曲线如图9所示,并将车致振动工况下各测点实测与模拟加速度峰值的汇总于表4。

表4 加速度峰值对比Table 4 Comparison of peak acceleraton

图8 测点横向布置示意图Fig. 8 Schematic diagram of lateral arrangement of measuring points

图9 各测点竖向加速度时程曲线Fig. 9 Vertical acceleration time-history curves of each measuring point
由表4可以看出计算和实测竖向加速度峰值比较接近,处于同一数量级,从而验证了模型空间耦合振动计算结果具有一定的可靠性。
4 不同结构参数对车站动力响应的影响
4.1 轨道梁高及站厅层柱截面尺寸对车站结构动力响应的影响
为了更好地探究车站结构动力响应受结构尺寸参数变化的影响,以单线满载B型列车120 km/h车速沿下行方向越行通过车站的工况为例,选取1.0,1.2,1.4,1.6 和1.8 m 5 组轨道梁梁高,1 m×1 m,1.1 m×1.1 m,1.2 m×1.2 m,1.3 m×1.3 m,1.4 m×1.4 m 5 组站厅层框架柱截面尺寸,分别建立不同结构尺寸的车轨站耦合分析模型,将计算得出的站厅层楼板和站台层楼板竖向动力响应最大值汇总于表5,探究轨道梁高与站厅层柱截面尺寸变化对站房结构动力响应的影响。
由表5可知,随着轨道梁高和站厅层柱截面边长的增大,车站站厅层楼板和站台层楼板竖向位移响应和竖向加速度响应均变化较大。为更直观地观察站厅层楼板和站台层楼板的竖向振动响应受轨道梁高变化的影响,将楼板竖向加速度动力响应绘于图10。

图10 车站结构竖向动力响应最大值随轨道梁高和站厅层柱截面尺寸变化折线图Fig. 10 Broken line diagram of the maximum vertical dynamic response of the station structure with the change of the beam height of the track and the section size of the floor column of the station hall
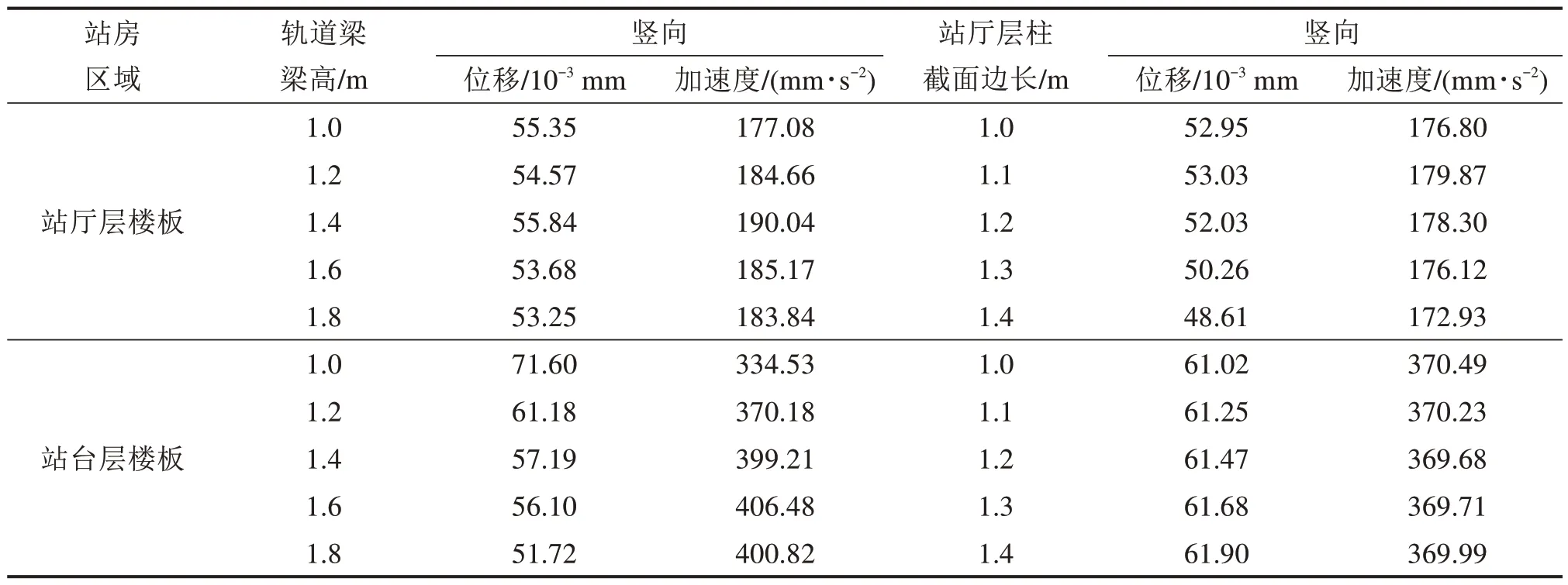
表5 不同轨道梁高及站厅层柱截面尺寸下车站不同区域动力响应最大值Table 5 Maximum dynamic response in different areas of the station under different height of rail beam and section size of hall column
从图10 可以看出,站厅层的竖向位移随着轨道梁高的增大呈减少趋势,竖向加速度则随着轨道梁增加呈增大趋势。站台层的竖向位移和竖向加速度则随着轨道梁高增加保持基本不变。而增大站厅层框架柱截面尺寸,站厅层的竖向位移有所减小,站台层竖向加速度、竖向位移和站厅层的竖向加速度则基本保持不变。
4.2 楼板厚度对车站结构动力响应的影响
以单线满载B 型列车以120 km/h 车速沿下行方向越行通过车站的工况为例,选取0.3,0.4,0.5,0.6 和0.7 m 5 组承轨层楼板厚度,0.16,0.18,0.2,0.22 和0.24 m 5 组站厅层楼板厚度,0.12,0.15,0.18,0.21 和0.24 m 5 组站台层楼板厚度,分别建立不同结构尺寸的车轨站耦合分析模型,将计算得出的站厅层楼板和站台层楼板竖向动力响应最大值汇总于表6,探究车站各层楼板厚度变化对站房结构动力响应的影响。

表6 不同楼板厚度下车站不同区域动力响应最大值Table 6 Maximum dynamic response in different areas of the station under different floor thickness
由表6可知,车站站厅层楼板的竖向位移和竖向加速度均随着承轨层厚度的增大变化较大,随站厅层站台层厚度增加则基本保持不变。为更直观地观察站台层与站厅层的竖向振动响应受各楼板层厚度的影响,将楼板竖向加速度动力响应绘于图11。

图11 车站结构竖向动力响应最大值随各层楼板厚度变化折线图Fig. 11 Line chart of maximum vertical dynamic response of station structure changing with the thickness of each floor
从图11 可以看出,随着承轨层楼板厚度增大,站厅层楼板和站台层楼板的竖向加速度减小最快。站厅层楼板厚度增大,车站站厅层和站台层楼板的竖向加速度响应变化很小,基本保持不变,故站厅层和站台层楼板的竖向加速度响应受站厅层楼板厚度变化影响很小。当站台层楼板厚度增大,站台层楼板的竖向加速度响有所减小,站厅层楼板的竖向加速度响应则基本不受影响,故站厅层和站台层楼板的响应受站台层楼板的厚度变化影响较小。
5 结论
1) 列车通过车站时,站厅层竖向位移随车速增加呈现增大趋势,站台层竖向位移则基本保持不变,而车站结构横向、纵向位移随着车速的增大均呈现增大后减小的趋势。车站结构的竖向加速度随车速增加呈增大趋势,且竖向加速度响应明显大于横向和纵向加速度响应,站厅层横向与纵向加速度响应随车速增大而呈增大趋势,而站台层横向与纵向加速度响应则基本保持不变。
2) 理论计算与现场实测得到的站台层、站厅层各测点峰值加速度误差较小,说明模型建立方法正确,分析模型能够有效地模拟真实结构的振动响应特性。
3) 对于此类“站桥合一”型车站而言,适当增大承轨层楼板厚度能够最为有效地减小车站结构站台层与站厅层的竖向加速度响应。其次是增加站台层楼板厚度,能明显减小站台层楼板的竖向加速度响应。再者是增大轨道梁梁高,能够显著减小站台层楼板的竖向位移响应。而改变站厅层柱截面边长或者改变站厅层楼板厚度,则对车站结构的动力响应影响很小。
