中低速磁浮列车滑模自抗扰悬浮控制算法
2023-03-29陈萍史天成于明月陈垟史炎
陈萍 ,史天成,于明月,陈垟,史炎
(1. 沈阳航空航天大学 民用航空学院,辽宁 沈阳 110136;2. 辽宁通用航空研究院,辽宁 沈阳 110136;3. 沈阳航空航天大学 自动化学院,辽宁 沈阳 110136;4. 西南交通大学 牵引动力国家重点实验室,四川 成都 610031)
近年来,中国轨道交通发展迅速,国家更加重视基础设施建设,轨道交通类型也更加多样。其中磁浮列车因为其爬坡能力强,与轨道间维持一定间隙,从而消除了悬浮架与轨道的摩擦磨损而受到广泛关注。目前国内已有的中低速磁悬浮运营线有北京磁浮S1线和长沙磁浮线[1]等,并有一些新结构磁浮列车被提出,优化了列车结构,列车性能有所提升[2]。为了确保乘客的安全,运营线路上列车的很多关键部件都有冗余设计,悬浮控制程序中90%左右的代码都用来故障诊断,真正的控制算法只占代码的10%左右。其中,间隙测量是保持稳定悬浮最重要的环节,理论上如果间隙的采样频率和采样精度足够高,只要控制器获取到间隙就可以实现基本悬浮。在运营线路中,每个控制点都冗余了三路间隙传感器、两路加速度传感器和两路电流传感器。测量间隙采用电涡流原理,后级信号处理采用相敏检波电路[3]或LDC1614[4]实现。实现悬浮控制的算法包括滑模控制[5-8]、自适应控制[9-10]、自抗扰控制[11-12]和滑模自抗扰控制[13-17]等,这些控制算法能够实现基本的悬浮,不同算法稳定悬浮时电磁铁中电流相差不大,所以算法的功耗基本一致。滑模控制的低频性能好[8],但参数调试较复杂,带宽较窄;自适应控制能够在不修改参数的情况下适应不同质量的悬浮架,没有繁琐的调参过程,但控制过程会有超调;自抗扰控制能够让悬浮间隙无颤振、无超调,但参数调试较复杂;滑模自抗扰控制同时拥有滑模和自抗扰的特性,抗干扰能力强且带宽较宽,但是李大字等[13-17]提出的滑模自抗扰控制将扩张状态观测器观测数据直接用于控制,未将读取观测数据和读取传感器数据的控制效果做对比,且文献中传感器精度高,测量准确,动态性能好,适合在干扰不剧烈的固定场合使用。而中低速磁浮列车的悬浮系统有很强的非线性,实际动态运行时会有复杂扰动进入系统,控制器需要获取的传感器信号种类多,安全性要求高,而扩张状态观测器观测的数据与实际数据有误差。目前运营线路主要存在的问题是悬浮架完全解耦,任何一个悬浮控制点的间隙或电流传感器失效,或控制板卡失效,悬浮控制点将无法正常悬浮,整个悬浮架就向失效一侧倾斜,导致列车无法正常运行[18]。较好的解决方案是加入更多的控制器和传感器冗余控制,这种方式增加了控制器的能耗,也增加了车重。如果只考虑电涡流传感器测量间隙,在列车遇到上下坡的时候,悬浮架会有敲打轨道的情况,特别是速度较快的情况下,敲打轨道现象更为明显,乘客乘坐体验感会很差,这也制约着磁浮线的运营速度[19]。控制器中需要加入对信号的微分抑制波动,但是直接微分会导致系统不稳定,悬浮架容易失稳,所以采用韩京清[20]提出的最速控制综合函数实现对信号的微分。本文基于运营线路现有控制器和传感器的基础上,针对上述这些问题,对比了状态反馈控制、直接获取传感器的滑模自抗扰控制、自抗扰控制和获取扩张状态观测器数据的滑模自抗扰的控制效果,并提出在电流传感器正常情况下采用传感器数据参与控制保证列车最优性能,电流传感器故障情况下采用观测数据参与控制保证列车正常悬浮,同时为了提升控制器的带宽,数据融合后间隙包含了被电涡流传感器滤掉的高频成分,加入了对间隙和加速度数据故障的判断,即使多个传感器同时故障也不会影响正常悬浮。通过仿真和实验验证了所提模型的优越性,提高了动态运行状态下悬浮可靠性以降低列车趴窝的风险。
1 磁浮列车数学模型
磁浮列车单个解耦后的控制点如图1 所示,F轨用于悬浮导向和列车降落时对车体支撑,控制器连接电磁铁,通过调整控制器产生的PWM 占空比调节电磁铁线圈中的电流,将电磁铁吸起一定的高度,使电磁铁与F轨之间间隔固定的距离,这个距离称为悬浮间隙。采用2 个IGBT 组成半桥电路实现对电磁铁电流的控制,因为即使一个IGBT被击穿短路,另一个IGBT 也能正常工作。4 个反接的二极管是防止电磁铁两端的电压过高击穿IGBT,将电磁铁中过大的能量反馈回DC330V 电网中。悬浮间隙通过安装在电磁铁上方的电涡流传感器测量得到[21]。

图1 磁浮列车原理Fig. 1 Schematic diagram of maglev vehicle
在理想条件下,车体的垂向运动方程可以表示为[22]
式中:F表示电磁铁产生的悬浮力;i表示电磁铁流过的电流;x表示空气间隙;μ0表示真空磁导率;N表示电磁铁线圈匝数;S表示正对横截面积。
垂向加速度随着间隙与电流的变化为
式中:m表示悬浮点的等效质量;fd表示受到的干扰力;g表示重力加速度。
电感量L随间隙的变化为
电磁铁两端的电压u与电流的关系为
式中:R表示电磁铁的等效电阻。
被控对象的状态方程可以表示为
式中:x1表示间隙;x2表示速度;x3表示电流。实际控制系统中,间隙、加速度和电流容易获取,而速度较难获取。d1,d2和d3表示传感器采集时引入的噪声,实际情况可获取到噪声波动的上界,仿真时设定d1,d2和d3为对应上界的随机噪声信号;y表示模型的输出,即间隙。
2 控制器设计
2.1 滑模控制器
滑模控制的原理是控制器根据当前间隙与目标间隙差值输出信号到执行机构,最终驱动被控对象使列车稳定悬浮,由于反馈回的当前间隙值会引入测量噪声,所以测量的间隙需要进行数据融合。
图2 滑模控制器Fig. 2 Sliding mode controller
根据式(5),输出的一阶导数为
输出的二阶导数为
输出的三阶导数为
式 中 :d表示等效噪声信号, 且
所以控制器的输出可以表示为
式中:v表示控制律辅助项,且表示噪声信号的上界。
设定滑模函数
式中:
证明:
对式(10)求导,并代入式(8)得
选择Lyapunov函数为
考虑到噪声信号的上界max|d| ≤η时,有̇≤0,此时根据LaSalle不变性原理,控制器与被控对象组成的闭环系统渐进稳定[23],当t →∞时,有
当η≥max|d|时,能保证系统稳定,但是η并不是越大越好,过大的η会导致系统的抖振。
在坡道向竖曲线过渡或竖曲线向坡道过渡的时候可能出现敲打轨道的现象,坡道可以分为上坡和下坡情况,如图3所示。

图3 有坡道的情况Fig. 3 When the ramp exists
如果只考虑上坡的情况,式(7)将会加入向心力
式中:θ为车体向心力与竖直方向的夹角;vveh表示车速;r表示轨道的半径。
综合考虑上下坡情况,则有
此时的向心力可以被加速度传感器检测到,考虑到轨道坡度较小,最大不超过7%,忽略θ变化,所以式(17)将会变为式(18)
输出的三阶导数为
反推出滑模控制器输出函数为
式中:̈2表示对加速度传感器信号的微分,此时控制器输出中已经融合了间隙、电流和加速度信号。但是在控制器设计中,对某一个信号求微分会导致系统不稳定,所以需要设计一种微分器。
2.2 滑模自抗扰控制器
滑模自抗扰控制器的核心为扩张状态观测器和跟踪微分器,参考韩京清[20]提出的自抗扰控制,首先设定两种逼近函数
式中:δ为消除高频颤振加入的线性区间长度;α为次方数;e为误差;z为包含了高频分量的误差项。

图4 滑模自抗扰控制器Fig. 4 Sliding mode active disturbance rejection controller
自抗扰控制利用“等时区方法”构造了一个近似的离散形式的最速控制综合函数,利用这种函数构造出的跟踪微分器可以快速、没有超调、没有颤振地跟踪加速度信号,并输出加速度的微分信号,状态方程可表示为
式中:ra为调整跟踪快慢的速度因子;h为采样时间;x01为加速度的跟踪输出;x02为加速度的微分输出。
对于获取所有传感器数据的滑模自抗扰控制器输出可表示为
式中:s与式(10)一致,但是s中̇d和̇d的值由与式(23)相同形式的跟踪微分器求得微分,̇的值由加速度传感器采集的数据̈积分得到。
非线性扩张状态观测器ESO的方程为
式中:β01,β02和β03为观测器增益系数;z1,z2和z3分别对应x1,x2和x3的观测值;a1和a2分别代表不同的次方数;eo表示观测间隙与实际间隙的差值;b0表示对控制器输出的放大系数。
WEI等[11]提出了自抗扰控制器输出公式为
式中:kp和kd分别表示自抗扰控制器的比例和微分系数。
对于获取观测器数据的滑模自抗扰控制器输出可表示为
式中:so表示滑模自抗扰控制器的滑模函数,且和c6表示观测器系数。
证明:
考虑对于观测间隙求导,则有
对于观测加速度
对式(27)中的so求导,则有
将式(25)、式(28)和式(29)代入到式(30)中,有
设定获取观测器数据的滑模自抗扰控制器的Lyapunov函数为
对式(32)求导得
考虑到将式(27)代入到式(31)中,同时确保η≥d,此时̇o≤0,所以系统渐进稳定,当t →∞时,有
式(24)可以看出获取所有传感器数据的滑模自抗扰控制达到稳定悬浮需要保证传感器正常,电流传感器失效将导致列车失稳。扩张状态观测器可以对电流传感器数据估计,正常运行时控制器采用式(24)的形式,但是此时扩张状态观测器会返回数据,电流传感器故障时,即z3与x3差值的绝对值大于阈值时,控制器变为式(27)的形式,所以只要间隙传感器正常列车就不会失稳。
2.3 状态反馈控制器
作为对比,引入LEE 等[24]提出的状态反馈控制,该算法类似于工程常用的经典PID控制,但采用直接读取多种传感器数据的方法而非在程序中对悬浮间隙做微积分处理,能够快速达到稳定条件。令得到x3=
所以控制器的输出可以写为
式中:k1为比例系数;k2为微分系数;k3为电流系数。该方法的缺点是必须准确估计车体质量,如果遇到质量变化较大的情况让等式平衡需要消耗时间调节,所以该算法最大的缺点是鲁棒性差。
2.4 数据融合
列车运行时会有多个电涡流传感器测量间隙,间隙的量程为0~20 mm,间隙传感器探头通过轨缝的时候,采集到的间隙值比其他通道大很多,此时该通道数据不可用,只有从其他通道获取的间隙数据,考虑到坏掉的间隙传感器输出为0 mm,则间隙传感器有效性判断函数为
式中:ng表示间隙传感器的数量,z表示有效值判断后的间隙值。
对于将间隙测量的结果融合到最终的间隙值中
式中:Kk是数据增益,用于减小数据的波动,为常数,关系到相位差。Kk越小,相位差越大,滤波效果好。但相位差过大会导致控制不及时,列车容易失稳,x为滤波后的间隙数据。
采用多个传感器测量加速度,加速度的量程为-5g~+5g,考虑到加速度传感器冗余,确认加速度传感器正常后将数据反馈到控制器中,对于加速度的判断为
式中:na表示加速度传感器的数量,a0i表示第i个通道的加速度值,a表示加速度数据。
在频域中间隙信号可表示为
式中:τ表示滤波器时间常数,X为间隙在频域的表示。考虑到输入的间隙测量信号可以分为高频区域和低频区域。电涡流传感器低频性能较好,但是高频性能较差;加速度传感器高频性能较好,但是低频性能较差。滑模自抗扰控制器的低频性能较好,但是高频性能较差,为了弥补控制器的高频性能,采用互补滤波的方式将测量的输入到控制器中,即低频采用电涡流传感器的数据,高频采用加速度的数据。即
式中:A表示加速度在频域的表示,̂表示最终融合后间隙在频域的表示,通过一阶向后差分算法可以将连续函数转为离散函数。转换函数为
将式(40)代入到式(39)中,得到间隙z 变换后的方程
式中:̂表示数据融合后的间隙。
化简并反变换得到离散后的迭代方程为
3 仿真与试验
根据磁浮列车的数学模型,采用MATLAB/Simulink 进行仿真,悬浮架参数如表1 所示,扩张状态观测器的参数如表2所示。仿真后将算法应用到磁悬浮试验线路中测试。

表1 悬浮架参数Table 1 Parameters of suspension frame

表2 滑模自抗扰控制器参数Table 2 Parameters of sliding mode active disturbance rejection controller
3.1 滑模自抗扰控制算法仿真
设定悬浮间隙为8.5 mm,坡道参数按照张锟等[19]设定,长度=40 m,半径r=1 000 m,坡度θ=40‰,k1=1 400,k2=1 200,k3=15,kp=1 600,kd=80,运行速度vveh=100 km/h,在第8 s 时进入上坡。通过滑模自抗扰控制器实现对磁浮列车的控制仿真,此时的控制器输出为式(27),结果如图5(a)所示,可以看出对于速度的估计比实际值偏大,基本能观测到控制器的电流信号。
通过仿真对比状态反馈控制、获取所有传感器数据的滑模自抗扰控制、自抗扰控制和获取观测器数据的滑模自抗扰控制,间隙变化如图5(b)所示,获取所有传感器数据的滑模自抗扰控制和获取观测器数据的滑模自抗扰控制能够较好地通过坡道,而状态反馈控制和自抗扰控制间隙会有0.47 mm 的波动。获取观测器数据的滑模自抗扰控制会有超调,因为观测值与实际值有误差,在正常运行情况滑模自抗扰控制是从所有传感器中获取数据,而不采用观测值。不同控制算法的仿真性能对比如表3 所示,4 种算法各有优势,自抗扰控制中的微分器不会造成系统发散,扩张状态观测器能根据间隙估计出速度和电流,对噪声抑制效果好。综合图5 和表3,获取所有传感器数据的滑模自抗扰控制因为传感器数据融合弥补了滑模控制器的带宽,跟踪微分器抑制了扰动。而扩张状态观测器提高了悬浮可靠性,为列车运行安全提供最后一道保障。

表3 不同控制算法仿真性能对比Table 3 Performance comparison of different control algorithms in simulation

图5 算法仿真对比Fig. 5 Simulation of algorithms
3.2 滑模自抗扰控制算法实测
悬浮控制板卡如图6(a)所示,采用TMS320F2 8379D 实现悬浮控制算法,DSP内部的双核实现对控制程序的冗余。FPGA 实现对传感器数据解码,间隙信号传输到DSP 的共享RAM 中,双核DSP 运行相同程序完成传感器数据融合和控制算法实现,并将目标占空比传回FPGA,FPGA 对双核反馈回的数据仲裁,最终产生PWM 驱动IGBT。控制器的输出为PWM 的占空比,与式(4)稍有不同,实际的测量电流偏小,因为斩波器开启时电磁铁两端电压就为330 V。因为有漏磁等其他因素存在,实车中还有一些损耗,导致列车起浮时的上升时间和调节时间与仿真相比更长了。
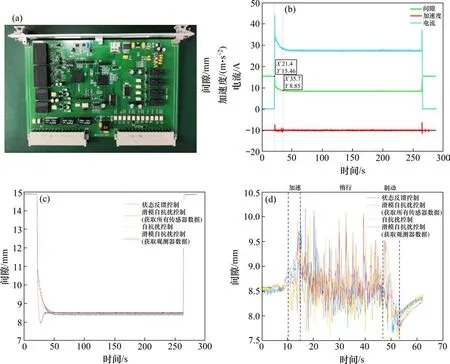
图6 实车测试图Fig. 6 Test of maglev vehicle
获取所有传感器数据的滑模自抗扰控制静浮实测的曲线如图6(b)所示,可以看出间隙的调节时间约为14.30 s,从间隙变化曲线可以看出,系统的过阻尼效果明显,鲁棒性强,这样能够防止悬浮过程中对车载设备造成过大的冲击,同时给乘客带来更好的乘坐体验。根据加速度的变化可以看出只有在起浮和降落时有较大的波动,加速度传感器采集到的加速度信号向上为正,车体受到的重力向下,所以稳定在-9.80 m/s2左右。根据电流的变化可以看出稳定悬浮时电流27.72 A 左右,只有起浮和降落时电流稍大一些以克服静置间隙浮起或平稳落地。各种控制算法的静悬间隙实测数据变化如图6(c)所示,动态运行间隙实测数据变化如图6(d)所示,列车从静止加速到15 km/h 惰行32 s 后制动,最终停止,算法的性能对比如表4 所示。其中状态反馈控制算法在静浮时波动大,动态运行时能根据传感器数据及时做出反应。获取所有传感器数据的滑模自抗扰控制静浮和动态运行性能较好,传感器能检测出实时的状态,但是调节时间长。自抗扰控制在静浮时因为有扩张状态观测器的存在,抗干扰能力强,但是动态运行时观测数据与实际有误差导致波动较大。仅获取观测器数据的滑模自抗扰控制在静浮时波动被有效抑制了,但是动态运行时同样由于观测数据与实际有误差导致间隙波动大。实测算法对比结果与仿真基本一致,而获取所有传感器数据的滑模自抗扰控制在故障工况下改用观测器数据却依旧能够保持稳定悬浮以坚持到回库检修,冗余设计提升了控制器的可靠性。

表4 不同控制算法实测性能对比Table 4 Performance comparison of different control algorithms in real vehicle
3.3 传感器数据融合实测
从图7(a)可以看出,由于轨缝的存在,3 个间隙传感器反馈回的间隙数据中有突变。在加入间隙传感器数据有效性判断后,输出的数据消除了突变点,加入滤波算法后,可以看出滤波后的间隙波动少了6.40%。加速和减速过程由于列车的惯性,间隙会有很大的波动,完全停止之后间隙逐渐恢复8.50 mm。

图7 传感器数据融合实测Fig. 7 Data fusion of sensors in maglev vehicle
从图7(b)可以看出处理后的数据包含了2 种传感器的数据,该判断算法在有一个加速度传感器故障时也会有加速度输出。加速度数据在数据融合后,间隙突变时加入了高频分量,如图7(c)所示。可见数据融合过程将2种传感器的频率特性都发挥了出来。
4 结论
1) 提出的滑模自抗扰悬浮控制算法,扩张状态观测器观测到的数据不仅用于对传感器故障判断,也可以在电流传感器故障的情况下直接用于控制算法,提升了控制器的可靠性。
2) 在对传感器数据融合时,首先判断了数据的有效性,并根据传感器频率特性提取了各传感器的有效信息,提升了控制器的带宽。
3) 在磁浮列车的悬浮控制板卡中运行程序,采用上位机软件获取悬浮间隙、电流和加速度,与MATLAB/Simulink 仿真相对比,调节时间和上升时间等指标与仿真有很大的差别,因为实车中有些损耗在仿真时被忽略了。
