不同温度下沥青自愈合行为的纳观表征与分析研究
2023-03-29詹易群吴昊宋卫民朱琳
詹易群,吴昊,宋卫民,朱琳
(中南大学 土木工程学院,湖南 长沙 410075)
沥青路面受到交通荷载和环境因素的反复作用,会引起沥青胶浆黏聚或黏附损伤的开展[1-2],最终导致整个路面性能的恶化[3-4]。沥青在高温下的流变特性和扩散性能对于其自愈合特性有十分重要的影响。沥青自身的黏滞流动作用会使它填充到微小裂缝中,填充的沥青和出现损伤的沥青会逐渐融合,从而促进裂缝的愈合[5-6]。这种自愈合行为对于路面的病害具有一定的抑制和修复作用,并在一定程度上恢复路面的强度和抗渗性能。沥青的自愈合行为一般发生在纳观尺度上,宏观试验获得的信息尚不能揭示沥青自愈合的机制。因此,从纳观尺度认识沥青材料的自愈合行为及机理具有十分重要的意义[5,7-8]。目前对沥青自愈合特性的研究主要分为2个方面:一方面是着重于通过试验获得与沥青材料自愈合行为相关的物理力学特性,另一方面则侧重于研究沥青材料自愈合特性对沥青混合料的力学性能与耐久性能的影响[9]。随着计算机技术的发展,越来越多的学者采用分子动力学(MD)来研究沥青的相关性能,从而获取一些无法通过宏观试验获得的现象和数据。MD 可以模拟给定周期内原子和分子的相互作用和力学行为,并计算分子模型的物理、化学和热力学特性,从而在纳观尺度给出材料行为的力学解释[7,10]。此外,该方法也被证明是研究沥青结合料的老化、水敏感性和损伤机理的有效方法。沥青的自愈合能力与其流变性能关系密切。实际使用过程中,沥青的自愈合能力受到温度、压力、组分等各种因素的影响[3,8,11]。BHASIN 等[12]首次采用MD 来模拟了沥青自愈合现象,认为沥青的自愈合与沥青的分子链的形态有一定的相关性。研究采用了具有不同支链长度的沥青质来进行模拟,研究结果表明,随着沥青分子的支链逐渐增多分子链逐渐缩短,沥青材料的自愈合速率也随之加快。SUN 等[13]在毛细管扩散理论基础上,将沥青自愈合分为润湿和扩散阶段。同时通过分子模拟技术分别分析了基质沥青和SBS 改性沥青的自愈合能力。该研究在阿伦尼乌斯方程的基础上,采用愈合指数对沥青的自愈合能力进行评价。结果表明SBS 改性沥青的自愈合性能更为良好。HE 等[14]采用MD对基质沥青、老化沥青和SBS改性沥青的自愈合过程进行了模拟与分析,模型的体积变化和扩散率等参数被用来表征沥青的自愈合效果。研究结果表明,沥青体积的“压缩”和沥青分子的“拉伸”是沥青微裂纹愈合的主要原因。SHEN 等[15]建立了具有不同裂纹宽度的小尺度MD 模型来研究沥青的自愈合机制,并探讨了裂纹宽度对自愈合效果的影响。研究结果表明,自愈合是由沥青分子的扩散机制所触发的,较高的温度会导致较高的分子扩散率,从而使得沥青材料获得更高的自愈合率;另外,无论是宏观还是微观层面,老化程度和裂缝宽度都会对沥青的自愈合效率产生重要影响。朱建勇[16]采用四组分沥青体系在不同温度下对沥青进行了分子动力学计算,研究了不同温度下均方位移的变化。结果表明,随着温度的增高,沥青的扩散系数增大,即沥青自愈合的速度也随之越快。柏林等[17]利用沥青四组分分析法建立沥青分子和裂缝分析模型,模拟了不同温度、压强和老化条件下沥青四组分在愈合时的扩散过程,得到了愈合模型的密度、均方位移曲线和各组分的扩散系数。结果表明,沥青在愈合过程中饱和分和芳香分的扩散速度最快,升温升压能够促进沥青分子运动;相同条件下,老化沥青愈合时的扩散系数明显小于未老化沥青。YU 等[18]为了准确了解内外部因素对于自愈合过程的影响,利用活化能研究了不同裂缝宽度及温度梯度下的愈合过程。结果得出微裂缝宽度对于自愈合的影响大于温度作用,老化后的沥青自愈合需要更长的时间与活化能。在扩散性方面,ZHANG 等[19]对沥青模型在不同温度下进行长达12 ns 的计算收集应力张量等数据,然后通过Green-Kubo 公式进行计算,得到了不同温度下的黏度。结果表明,模拟的沥青模型与SHRP 具有相同的数量级,同时与KHONG 等[20]研究的样品沥青具有相似的黏度和温度依赖关系。丁勇杰[21]采用了直接计算法和扩散系数计算法来计算了沥青的黏度,以此验证沥青模型建立的准确性。通过扩散系数计算法,发现黏度与扩散系数具有较高的相关性,从而验证了沥青模型的准确性。XU 等[22-23]通过建立沥青的老化模型,对老化沥青的基础性能进行模拟分析。结果表明,由于老化后的沥青具有更高的极性,所以导致内聚能密度更低,扩散性能更差;同时老化沥青较于基质沥青具有更高的活化能屏障,这导致其自愈合能力降低。HU 等[24]基于分子动力学对橡胶沥青进行热力学计算发现,随着橡胶含量的增加,沥青之间的自愈合性能明显减缓,橡胶改性剂在一定程度上弱化了沥青组分之间的扩散团聚作用。SUN 等[25]基于Arrhenius 方程提出自愈合参数对SBS 改性沥青进行评价,结果表明该参数可以较好的反应不同温度下高黏沥青的自愈合性能,同时由于SBS 改性剂的存在,改性沥青的扩散系数高于基质沥青,拥有更强的自愈性能。本文构建了沥青纳观分子自愈合模型,模拟了沥青在不同温度条件下的分子运动状态。相比于现有的研究,本研究基于AAA-1 沥青分子模型,构建了四组分12 类分子体系建立了沥青分子模型;从中温到高温,模拟了3 种温度下(293.15,313.15和333.15 K)沥青的自愈合行为;同时采用密度、相对浓度、内聚能密度和自由体积分数等多指标来评价沥青的流变和扩散特性,为沥青材料在纳观尺度的特性与机理研究提供了新的思路。
1 分析模型的建立
1.1 沥青纳观分子结构模型
本文基于LI等[26]提出的AAA-1沥青分子模型,采用四组分12 类分子体系建立了沥青分子模型,其中各组分的代表分子模型如图1所示。

图1 基质沥青的分子结构模型Fig. 1 Molecular structure model of the virgin asphalt
在建立了12 种分子模型并进行能量最小化之后,利用MS 中的Amorphous Cell 模块中按一定的数值比例加入沥青12 类分子的各个组分(见表1),创建了沥青的无定形晶胞。然后,为了使沥青分子更加接近真实状态,选择Forcite 中的Dynamic模块对沥青分子组成体系进行了5 000 次循环的几何优化、弛豫、NPT 模拟运算、退火处理、NVT模拟运算,最终得到稳定的沥青分子结构分析模型,如图2所示。

表1 沥青模型的组成Table 1 Compositions of the asphalt model

图2 沥青分子结构纳观模型(按分子类型显示)Fig. 2 Nanoscopic model of the molecular structure of asphalt (shown by molecular type)
1.2 沥青分子模型准确性验证
为了使模拟结果准确,本文选取沥青的密度和分子内部径向分布函数g(r)对分子模型的准确性进行验证。径向分布函数是反映了材料内部分子分布与聚集的情况。298 K 弛豫后的沥青密度为0.984 g/cm3;该温度下沥青的密度一般在0.90~1.04 g/cm3之间[27-28],本研究得出的沥青密度基本符合已经得出的结论。材料分子间的相互作用力一般可以通过g(r)来反映,g(r)的大小表明结构的无序化程度。利用Forcite 计算模块对g(r)进行提取,结果如图3所示。对于沥青而言,分子之间氢键可影响的范围为2.6~3.1 Å,范德华力可影响的范围为3.1~5 Å。从图3可以看出,g(r)在3 Å左右开始减小,而在5 Å 后曲线趋于平缓并趋近于1。结论于实际情况相一致[29]。因此,通过沥青密度与径向分布函数模拟结果的对比,认为该模型可以反映真实的沥青分子。

图3 沥青分子模型内部径向分布函数Fig. 3 Radial distribution function of intra-molecular in asphalt molecule models
1.3 沥青材料自愈合分析模型
本研究利用沥青分子模型在设计温度下的扩散行为来模拟自愈合过程,选用NPT 系统进行模拟。随着温度的升高,裂缝两侧的沥青分子发生自由流动,然后相互扩散与融合。采用Nose-Hoover 方式控制系统温度。当达到相对较高的温度时,模型中的分子移动得更快,使得裂缝两侧沥青分子表面更容易相互靠近与融合。
本文在模拟沥青自愈合行为时,先在不同的温度下对沥青分子模型进行晶胞弛豫,然后再通过Build layers 命令建立包含模拟裂缝的层状分析体系,同时对层状体系模型进行5 000 次迭代的几何优化得到最终的分析模型。层状体系模型一共包含3层结构,其中左右两层均为相应温度下的沥青层模型,中间层为10 Å 的真空层,用来模拟自愈合时的微裂缝。再对模型进行能量最小化的几何优化,最终在NPT 系综、相应温度下进行模拟。温度是影响其自愈合及扩散能力最直接的因素。本文的自愈合过程模拟考虑以下3 个温度的影响:293.15 K(20 ℃), 313.15 K(40 ℃)和333.15 K(60 ℃)。不同温度下层状模型能量变化结果如图4所示。从图中看出,由于层状模型中间裂缝的存在,在20 ps 前模型内部的能量波动较为剧烈,在30 ps 后模型内部的能量趋于稳定,结构达到平衡状态。如图5 所示,为333.15 K 下,自愈合初始模型及热动力学计算后的模型。为了增加模拟结果的直观性,将微裂缝两侧的沥青用不同的颜色显示。

图4 不同温度下层状模型能量变化Fig. 4 Energy variation of layered model at different temperatures

图5 沥青自愈合行为模拟Fig. 5 Asphalt self-healing behavior simulation
2 沥青自愈合行为的表征
本文主要是通过分析模型在密度、自由体积、浓度以及分子间隙上的变化来描述沥青的扩散与自愈合行为。内聚能密度(CED)和自由体积分数(FFV)在一定程度上可以反映沥青材料的宏观流变特性和变形能力。其中,CED 是指的单位体积的物质完全克服内部分子相互作用力所需要的能量,是用来描述物质内部分子间相互作用力大小的一个量。在MS中CED是对粒子位置坐标进行二次计算后得出的。内聚能密度是指的单位体积的物质完全克服内部分子相互作用力所需要的能量,是用来描述物质内部分子间相互作用力大小的一个量。沥青分子结构体系的内聚能密度可以通过式(1)计算得到:
式中:Ecoh为分子的内聚能;Einter为分子间的能量;Eintra为分子内部的能量;Etotal为系统总的能量;< >为NPT 或者NVT 系综的平均值;V为分析结构系综的体积。
自由体积分数FFV 是指分子结构中自由体积占据总体积的百分比,而自由体积指的是由于分子链的不规则排列而形成空隙所占的体积,体系中FFV 的大小一定程度上可以反映分子链可以自由运动的能力。在NPT 系统内,FFV 越大代表分子之间的空隙越大;FFV 越小说明分子之间的空隙越小,系统越密实,也可以反映出沥青的融合度更高。在MS 中,是采用硬球探针模型来对物质的自由体积和占有体积进行探索和描述。硬球可以进入的区域就是自由体积的区域。计算时选取的Connolly radius 为0 Å,计算出的自由体积为模型中除分子结构所占有的体积之外的所有空间的体积。FFV可以根据式(3)计算得到:
式中:VO为分子结构的空闲体积;VF为分子结构的自由体积。
分子的相对浓度表示的是沿垂直于轴划分的块中含有粒子的浓度占总体浓度的比例,可以反映出模拟裂缝两侧沥青在不同温度和时间下的扩散范围。在MS 中对相对浓度的分析主要是将晶胞沿着垂直于分析坐标轴划分为若干个块,计算每块单位体积中所含原子数与整个晶胞单位体积中所含原子数之比,即为相对浓度;然后将得到的每块的相对浓度用高斯函数进行拟合,最终得到其分布曲线。即:
式中:ci为每一块中的单位体积所含的原子数;Ni为区域内原子的数目;Vi为区域的体积;ctotal为整个晶胞单位体积所含原子数,R即为相对浓度。因为沥青自愈合模型是沿着Z轴建立的,所以根据Z轴的相对浓度变化情况可以用来分析自愈合情况。通过分析相对浓度分布状况的变化,可以从分子运动的角度来解释沥青自愈合能力和效率变化的原因。
3 自愈合行为模拟结果分析
本文选取中高温条件下(293.15,313.15 和333.15 K)的热动力学模拟计算来反映不同温度对沥青自愈合能力的影响。
3.1 密度和沿Z轴晶胞长度
对分子模型进行NPT 系综模拟时,材料的体积和密度都会随着温度的变化而变化。本文通过分析沥青的密度和体积的变化来反映其自愈合过程中的扩散行为。沥青自愈合过程可以通过分子动力学的2 个特征阶段来进行描述:第1 阶段:裂缝两侧的沥青层表面的重新排列与相互靠近,对模拟的裂缝逐渐进行填补的过程;第2阶段:两侧沥青层完全接触,并开始相互扩散,最终融合在一起。由于模拟时沿着Z轴建立了裂缝,所以在自愈合过程中沿Z轴的胞长变化可以很好的表征沥青自愈合的程度。本文分子动力学模拟得到的自愈合过程中沥青的密度和Z轴的胞长随时间的变化规律如图6和图7所示。
由图6 和图7 可以看出,在333.15 K(60 ℃)温度下,180 ps左右模型的体积与密度达到平衡。这是由于2层沥青层完全相同,并且此时两侧的沥青完全接触并彼此填充了空隙,接下来2层沥青层开始进入扩散阶段。 体系稳定后的密度为0.988 g/cm3,这与沥青在333.15 K(60 ℃)下的密度相近,表明模拟裂缝两侧的沥青层融合良好。同时,由于在NPT 条件下进行了热动力学模拟,所以材料的体积是随着两侧沥青层相互扩散填补空隙而逐渐减小的。

图6 不同温度下自愈合分子体系密度随时间的变化Fig. 6 Variation of self-healing molecular density with time at different temperatures
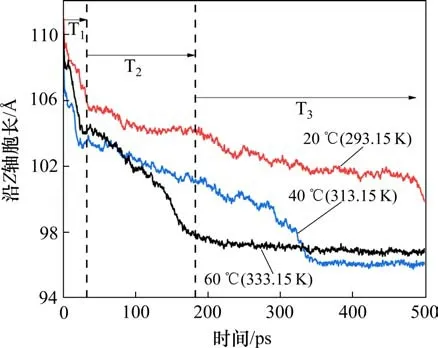
图7 不同温度下Z轴晶胞长度随时间的变化Fig. 7 Variation of Z-axis cell length with time at different temperatures
对于313.15 K(40 ℃)温度而言,与333.15 K(60 ℃)的沥青自愈合的模拟过程相似,但是密度和体积相较于333.15 K(60 ℃)时均有下降,同时达到平衡的时间在320 ps 左右,相较于333.15 K(60 ℃)要晚一些,这表明随着温度的升高,沥青的扩散能力增强和效率变大。在293.15 K(20 ℃)温度下,体系密度相较于其他两个温度最小,模型体积最大。这是由于自愈合行为在纳观尺度上分为3个主要阶段(见图7):以333.15 K为例,阶段1,在两侧沥青间隔较远时,分子间作用力较弱的情况下胞长快速减小的T1过程;阶段2,当两侧沥青层相对靠近以后,分子间作用力变大,使得胞长减小速度降低的T2过程;阶段3,当两侧沥青层完全接触以后,胞长不再改变,这是自愈合的T3过程。而在293.15 K(20 ℃)下,同样的模拟时间,沥青模型只进行到了T2过程,两侧沥青逐渐靠近并相互接触,填补了彼此空隙。对于T3过程而言,由于并未完成完全接触,所以不存在扩散阶段。这也就导致了在293.15 K(20 ℃)温度下模型体积相对较大,而密度较小的情况。
3.2 相对浓度
图8 所示为初始情况,293.15 K(20 ℃),313.15 K(40 ℃)和333.15 K(60 ℃)温度条件下模型沿Z轴的相对浓度变化情况。从模拟结果可以得到两层沥青层扩散融合区域的大小变化,通过与初始状态对比可以解释不同温度条件对于沥青材料自愈合能力的影响。

图8 不同温度条件下沥青自愈合过程相对浓度结果Fig. 8 Relative concentration results of asphalt self-healing process under different temperatures
根据初始情况下的相对浓度曲线可以观察到,在45 Å~61 Å之间相对浓度等于0,这一段代表的是沥青自愈合模型中的中间模拟微裂缝层。从模拟结果可以看出,在初始情况下相对浓度的峰值接近于2,而在不同温度下进行了500 ps 的热动力学计算后,相对浓度值均接近于1。这是由于沥青的扩散运动使左右两层的沥青分子逐渐扩散并填满到整个模型中,且相对浓度是一个比值,所以此时相对浓度均接近于1,因此相对浓度的变化可以反映沥青层的自愈合过程。在293.15 K 下,相对浓度的曲线在45 Å~61 Å 有一段凹陷,这说明此时的沥青自愈合模型经过500 ps的热动力学计算后,仍然存在一定的空隙,未达到完全接触状态,这表明中低温下,分子运动速率较为缓慢,导致沥青自愈合模型未达到完全接触状态。
3.3 内聚能密度与自由体积分数
本研究分别对不同温度模型的内聚能密度CED 和自由体积分数FFV 结果进行了对比分析,如图9所示。模拟结果显示,当温度从293.15 K 升高到313.15 K 时,CED 升高了7.7%,说明随着温度的升高,沥青材料流动性增强而抗变形能力减弱;当温度从313.15 K 升高到333.15 K 时,CED降低了约0.6%,说明当温度上升到一定程度(313.15 K)后继续升高温度对沥青的内聚能不会产生显著的影响。自由体积分数(FFV)随温度的变化与CED 正好相反,293.15 K 时的FFV 最大,313.15 K时最小,但FFV在313.15 K和333.15 K时的差异非常小。293.15 K时的FFV最大是因为经过了500 ps的热动力学计算,并未使得自愈合模型进入扩散阶段,此时中间层仍然存在很大的空隙可以让沥青分子链进行自由运动;中间层的空隙也使得分子间的相互作用力变得更小,即此时的CED 变小,宏观下就会表现出材料抗变形能力的降低。图10 所示为CED 与FFV 之间的相互关系,可以看出CED与FFV结果具有一定的线性相关性,可以用来描述沥青材料自愈合行为的扩散融合效果。但是,由于本研究中在中温时只选择了293.15 K 一个温度,在高温时只选择了313.15 K和333.15 K 2 个温度,结论具有一定的局限性;以后的研究中会选择更多的温度来阐明内聚能密度和自由体积分数的关系。

图9 自愈合模型的CED和FFV分析结果Fig. 9 CED and FFV results of the self-healing model

图10 CED和FFV的相关性Fig. 10 Correlation between CED and FFV
4 结论
1) 沥青的自愈合行为在纳观尺度上主要包括2个阶段:运动至完全接触阶段和扩散阶段。运动至完全接触阶段是体积发生变化的主要阶段,当达到完全接触状态,自愈合模型的体积会达到一个稳定值。同时,自愈合模型的体积和密度均会随着温度的变化而变化,达到稳定后均能满足随着温度越高,体积会越大密度会越小的趋势。
2) 从相对浓度上看,初始的自愈合模型存在2个峰值和1个谷值,这个谷值即可代表沥青层之间的空隙。随着扩散时间的延长,自愈合模型的空隙明显减小并逐渐消失。在293.15 K 下进行的500 ps热动力学计算仍然使得自愈合模型存在一定空隙,这说明293.15 K 下自愈合效率差。这表明随着温度的升高,沥青材料自愈合效率会有所提高。
3) 当温度从293.15 K 升高到313.15 K 时,CED和FFV的变化较为明显;但当温度从313.15 K升高到333.15 K 时,CED 和FFV 的变化非常小,说明当温度上升到一定程度(313.15 K)后继续升高温度对沥青的内聚能和自由体积分数不会产生显著的影响。内聚能密度CED 与自由体积分数FFV具有一定的相关性,可以用于描述沥青材料自愈合的扩散融合效果。后续的研究中会选择更多的温度来阐明内聚能密度和自由体积分数的关系。
