面向廓形质量的钢轨打磨模式优化决策方法
2023-03-29姜曼杨岳丘文生邓银强
姜曼,杨岳,丘文生,邓银强
(1. 中南大学 交通运输工程学院,湖南 长沙 410075;2. 广铁铁路(集团)公司 广州大型养路机械运用检修段,广东 广州 511400)
钢轨打磨是改善轮轨关系、提升列车运行品质、改善与消除病害的主要技术手段,通过钢轨打磨可以有效去除钢轨表面损伤缺陷,使轮轨匹配关系恢复至理想状态[1-3],延长钢轨的使用寿命。目前,现场钢轨打磨作业大多依靠工程技术人员的经验,根据服役钢轨廓形病害类型从已有打磨模式库中选取合适的打磨模式,受到主观经验的影响,对于同一条打磨线路,可能会出现多种打磨策略[4-5],这不仅增大了作业的工作量,而且无法准确控制钢轨打磨质量,严重时可能导致不良廓形的出现,对列车运行安全造成重大影响。因此,科学合理地确定打磨模式成为钢轨打磨领域的热点研究问题,UHLMANN 等[6-7]分析了钢轨打磨的影响因素,通过对比不同工艺参数组合对打磨结果的影响,提出了符合钢轨打磨条件的钢轨打磨策略;GRASSIE[8]综合考量打磨周期、作业质量及经济性的影响,提出了RCF(Rolling Contact Fatigue)方法,该方法对钢轨波磨和内侧剥落等问题起到了改善作用。王军平[9-11]等对打磨量与打磨参数进行了研究,在此基础上建立了打磨列车在不同打磨角度和打磨功率下的数值计算模型,实现了打磨模式的个性化生成。上述方法均在一定程度上提高了打磨模式与待打磨钢轨的匹配度,但受实际线路情况复杂、打磨列车车型不同、各区段钢轨的实际廓形或病害差异等因素的影响,按照现有研究方法或人工选择的打磨模式进行钢轨打磨,形成的钢轨实际廓形往往不能很好地与钢轨目标廓形匹配,因此亟需研究一种考虑线路实际情况、面向廓形质量的钢轨打磨模式决策方法。由于打磨模式的优劣取决于打磨后钢轨廓形的质量,因此本文以钢轨打磨廓形质量指数(GQI,Grinding Quality Index)作为评判打磨模式优劣的指标,采用NURBS 自由曲线造型方法描述钢轨打磨前后的廓形,通过分析钢轨打磨列车多个砂轮对钢轨的作用机理,构建包含打磨模式参数的钢轨打磨廓形预测模型,实现钢轨打磨廓形及其质量指数GQI 的准确预测;在此基础上,设计钢轨打磨模式优化决策算法,实现最优钢轨打磨模式的快速科学决策,从而有效控制钢轨打磨质量,提升钢轨打磨模式的决策效率。
1 基于NURBS 的钢轨打磨廓形质量指数计算
1.1 钢轨廓形的NURBS描述
钢轨廓形曲线是钢轨打磨廓形质量指数数值计算的重要依据,由于服役中的钢轨在轮轨作用力及自然环境的影响下廓形形状复杂,特征点缺失,普通曲线拟合方法难以支持钢轨打磨质量评估过程中的指标计算,NURBS 曲线拟合方法用非均匀样条替代了传统短线段,在几何精度、连续性和代码长度等方面都具有更高的优越性[12]。一条三次NURBS曲线定义为[13]:
其中u为节点矢量,Ni,3(u)为B 样条基函数,ωi为权因子,di为控制顶点,i=0, 1, 2, …,n。
提取钢轨轨头断面廓形的坐标信息Pi{xi,yi} (i=0, 1, 2, …,n)作为构建NURBS曲线的型值点,用来进行轨头断面廓形的NURBS 曲线的反向求解,其对应的节点矢量为由弦长参数化法和Cox-deBoor 递推公式[13]计算得到B样条基函数,由此建立求解控制顶点di的目标方程组:
更改权因子可以实现曲线的局部修改,初始权因子取1,由控制顶点di与B 样条基函数即可构建符合打磨后钢轨轨头断面廓形特点的NURBS 参数模型C1(u)。
1.2 钢轨打磨廓形质量指数的计算
钢轨打磨廓形质量指数可以定量反映钢轨打磨后断面廓形与打磨目标廓形的偏差,以此衡量不同钢轨打磨模式的打磨质量[14],偏差的准确计算是求解GQI的核心。如图1所示,钢轨的非工作侧边LZ与钢轨下颚角CZ具有较明显的形状特征且受到的损伤较小,以2个线段为基准,将钢轨打磨后断面廓形与打磨目标廓形对齐。按照测点选取准则[14]在打磨目标廓形的轨顶和工作边的轨侧上选取N个采样点,相邻采样点的横坐标数字化增量为0.7 mm,采样点Pi处的法线与打磨后断面廓形曲线CL(u)有且仅有一个交点Qi,交点与采样点间的距离|PiQi|即为打磨后断面廓形在采样点处的偏差。

图1 钢轨廓形质量指数计算基本原理Fig. 1 Calculation principle of rail profile quality index
偏差|PiQi|小于某一阈值Δ 的采样点总数记为nr<Δ,则钢轨打磨廓形质量指数GQI 的基本计算公式为:
准确计算打磨后断面廓形和打磨目标廓形的偏差是精确计算GQI的关键步骤,为便于N个采样点处法线方程的连续计算,利用采样点坐标信息构建打磨目标廓形的NURBS 模型CT(u),对于3 次NURBS 参数曲线CT(u),在任意一点ui处的1 阶导矢是:
则第i个采样点(xi,yi) 处的法线方程为:y-yi=-(x-xi)/C'(u),若(m0i,n0i)和(m1i,n1i)分别为法线方程上确定的2点参数坐标,dui和dvi为廓形曲线CL(u)的控制顶点,则求解交点Qi(u,v)的目标函数应为[11]:
其中,F(t)为含有B 样条基函数的非线性方程,应用区间分析的思想[15],利用方向包围盒(OBB,Oriented bounding box)算法快速定位含有交点的包围盒,将其作为区间迭代的预设区间,在预设区间内应用Newton 区间迭代算法进一步求解交点区间,在交点区间内给定初值,通过牛顿迭代法求出零点,即采样点处法线与打磨后断面廓形曲线的交点Qi。依次计算N个采样点处的偏差|PiQi|,设定阈值Δ,筛选出符合|PiQi| <Δ 的采样点个数nr<Δ,代入式(3)即可求得打磨后的钢轨打磨廓形质量指数GQI。
2 面向钢轨打磨廓形质量指数的打磨模式优化决策
2.1 钢轨打磨模式及打磨过程分析
钢轨打磨列车是钢轨打磨施工的主要技术装备,其在每股钢轨上方设有24 个可调整角度的打磨砂轮,打磨砂轮的摆角、排列顺序、打磨功率等工艺参数均可进行调整,这些工艺参数的组合可以编制为不同的打磨模式,改变砂轮摆角、打磨功率及其排列顺序这3个打磨模式参数,可以控制砂轮的打磨状态。针对不同种类的钢轨病害,铁路养护部门根据钢轨的最终打磨状态将打磨模式进行分组,在打磨施工前需根据钢轨的病害从相应的打磨模式组中选出一种打磨模式进行作业。
图2 为打磨列车的工作过程示意图,如图所示,砂轮沿钢轨呈纵向排列,单个磨头砂轮与钢轨轨头部分接触,砂轮以转速n旋转,在正压力Fn的作用下对钢轨进行磨削作业。若列车行进速度vt和打磨功率P恒定,当打磨时间t足够小时,砂轮直接作用于钢轨断面廓形,砂轮在钢轨断面上的磨削面积S为S=K0P34/v5/4t,K0是在行进速度v0,打磨功率p0时进行的磨削实验后确定的常量,因此打磨功率P可用目标磨削面积Sy表示,由此打磨模式可通过设定砂轮摆角、排列顺序及目标磨削面积来控制。

图2 钢轨打磨过程示意图Fig. 2 Diagramatic sketch of rail grinding process
2.2 面向打磨模式的钢轨打磨廓形质量指数预测
从2.1 小节的分析可知,钢轨的最终打磨状态由所选择的打磨模式决定,通过预测并对比采用模式组内不同打磨模式进行作业后的钢轨打磨廓形质量指数,即可从模式组中筛选出最适合待打磨钢轨的打磨模式。由1.2 小节可知,GQI 利用打磨后断面廓形与打磨目标廓形的偏差通过公式(3)进行求解,在尚未打磨的情况下无法对GQI 进行计算,因此实现对打磨后钢轨断面廓形的精确预测是对比GQI进而确定最优打磨模式的前提。
为实现打磨后钢轨断面廓形的预测,从几何角度分析单个砂轮的打磨过程的数学关系,将多个砂轮的打磨过程简化为单个砂轮以打磨模式设定的摆角顺序和功率循环作业于同一钢轨断面[16]。单个砂轮与钢轨轨头的接触几何关系如图3所示。

图3 打磨砂轮与钢轨轨头几何关系Fig. 3 Geometric relationship between grinding wheel and rail head
摆角为θ的打磨砂轮底部在钢轨断面上投影为一段直线段,起始位置为A'B',在C'点与钢轨廓形相切,打磨砂轮以一定进给步长对钢轨断面进行磨削,即直线段沿砂轮轴线MN从初始位置A'B'不断移动到AB,移动的距离为打磨深度d,砂轮与廓形重叠的阴影部分为目标磨削面积Sy[17]。图4 阴影部分为第i个砂轮在钢轨断面上的实际磨削面积Si,设定砂轮打磨功率下的目标磨削面积为Siy,若Si与Siy的差值满足|Siy-Si|≤ε时,砂轮停止沿MN方向的进给,结束单个砂轮的打磨作业。
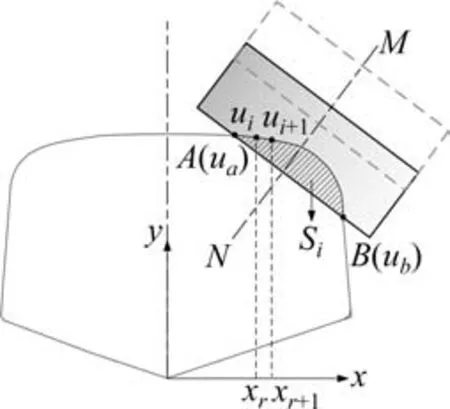
图4 打磨后断面廓形预测的基本原理Fig. 4 Basic principle of profile prediction after grinding
为求解实际磨削面积Si,构建钢轨断面廓形的NURBS曲线模型C0(u),则磨削面积的求解可以转化为NURBS 曲线与直线的积分差值计算,钢轨廓形曲线与砂轮底部端线相交于A 和B2 点,其节点矢量为ua和ub,为提高计算效率,将内节点区间[ui,ui+1]∈[ua,ub]内的NURBS 曲线转化为Bézier 曲线, 单段 Bézier 曲线参数形式为Pi(t)=(x(t)),y(t)),0 ≤t≤1, 对应的4 个权因子为{ωi0,ωi1,ωi2,ωi3},控制顶点为{di0,di1,di2,di3},单段Bézier曲线以多项式形式表示为:
则内节点区间[ui,ui+1](对应参数区间[lr,lr+1])内的打磨面积为:
单个砂轮磨削面积Si可以由区间[ua,ub]范围内的内节点区间打磨面积累计求得,经过打磨后的钢轨断面廓形由直线段AB及其两端初始断面廓形组成,以测点选取准则在直线段AB上提取采样点,更新钢轨断面廓形NURBS曲线Ci(u)。若磨削面积Si满足|Siy-Si|≤ε,根据打磨模式参数中设定的砂轮排列顺序,下一个砂轮继续进行作业,直到24个砂轮全部作用完成,最终的廓形曲线C24(u)即为图1中的钢轨打磨后断面廓形,由此实现了钢轨打磨后断面廓形的预测。结合1.2 所提出的GQI数值计算方法,在钢轨打磨目标廓形上选取N个采样点,依次计算采样点处钢轨打磨后断面廓形与打磨目标廓形的偏差,代入公式(2)即可求解GQI,从而评估打磨模式的打磨质量。
2.3 钢轨打磨模式优化决策算法
针对同一类钢轨病害,相应模式组中的多种打磨模式均具有改善作用,但打磨效果因钢轨表面损伤情况不同有所差异,为最大限度修复钢轨损伤、延长钢轨寿命,需要从多种打磨模式中筛选出最适合当前钢轨的打磨模式。钢轨打磨廓形质量指数可以量化打磨模式与待打磨钢轨的匹配程度,通过对比不同打磨模式下的GQI,即可为不同损伤情况的待打磨钢轨筛选出最优打磨模式。钢轨打磨模式决策本质上是不同打磨模式下的GQI寻优的过程,首先需要构建钢轨打磨模式寻优过程的稳定数学模型。以钢轨打磨廓形质量指数为打磨质量的评价指标,建立如式(8)的钢轨打磨模式的寻优函数:
式中:Mj为模式组中的第j种打磨模式,记为Mj(αi,Siy,)(i=1,2,…,24;j=1,2,…,M), 其 中αi(i=1,2,…,24)为砂轮摆角,Siy(i=1,2,…,24)为砂轮目标打磨面积。
对于同一钢轨断面,打磨列车底部24 个砂轮以其纵向排列顺序依次对其作用,以砂轮底面直线推进模拟砂轮作用过程,单个角度砂轮完成打磨后更新钢轨廓形,以便下一个角度砂轮计算,直至所有砂轮完成打磨过程,根据最终的钢轨打磨断面廓形计算当前打磨模式下的GQI,更换打磨模式参数,计算j种打磨模式下的GQI,最大值对应的打磨模式即为最优打磨模式。基于以上分析,可形成如下的钢轨打磨模式优化决策算法:
1) 输入待打磨钢轨廓形离散数据,构建钢轨断面初始廓形NURBS曲线表达式C0(u)。
2) 判断待打磨钢轨的主要病害,从钢轨打磨模式库中读取与之匹配的M种打磨模式,模式参数为Mj(αi,Siy)(i=1,2,…,24;j=1,2,…,M)。
3) 根据第j种打磨模式,设定打磨模式参数,砂轮序号为i,砂轮摆角为αi,构造砂轮底面直线参数化方程Li,砂轮直线推进步长h,目标打磨面积为Siy,误差阈值为ε。
4) 砂轮直线以步长h推进,计算钢轨断面廓形曲线与砂轮底面直线Li围成的磨削面积Si。若|Siy-Si|≤ε,则更新打磨后的廓形曲线Ci(u),反之,推进步长迭加,重新计算Si。
5) 更新砂轮序号,重复执行3)至24 次,得到24 个砂轮打磨后的钢轨廓形曲线C24(u),计算该打磨模式下的钢轨打磨廓形质量指数GQIj。
6) 更新打磨模式,重复执行3)~5),将M个打磨廓形质量指数由大到小排序,其排列顺序即为优化决策排序,排名第1的打磨模式即为当前钢轨打磨作业中的理论最优打磨模式。
3 钢轨打磨模式优化决策实例分析
3.1 钢轨断面廓形数据采集
为验证钢轨打磨模式优化决策算法的有效性,以京广线岳阳段某一位置的一段已产生病害的钢轨为实验对象,应用SmartRay 非接触式钢轨廓形激光检测装置对打磨作业前钢轨断面的实际廓形进行测量,图5为现场实验图,激光线对应的测量数据即为钢轨廓形原始坐标信息。

图5 钢轨数据采集实验现场Fig. 5 Experimental site of rail profile data acquisition
实验中采集的数据点数量巨大,为提高计算效率,结合钢轨数据点的曲率信息,应用k-余弦曲率采样法对钢轨廓形原始数据进行筛选。如图6为筛选后的钢轨廓形数据点,可以看出,轨头左侧轨距角处磨损较少,为圆滑曲线,右侧轨距角处出现尖角状凸起,为轮轨作用所形成的肥边,因此该段钢轨出现的主要伤损类型为肥边。

图6 筛选后的钢轨廓形数据Fig. 6 Filtered rail profile data
3.2 钢轨打磨模式决策
根据该病害情况,从打磨模式库中选取针对肥边的7种打磨模式,如图7所示,其中:图7(a),7(c)为打磨1车的41号、45号、47号和49号4种打磨模式的参数,图7(b),7(d)为打磨5 车的42 号、46 号和48 号3 种打磨模式的参数,图中每条曲线代表了一种打磨模式;由图7(a)和7(b)可以看出:砂轮打磨功率集中分布在55,60 和65 kW,打磨功率越大打磨能力越强;由图7(c)和7(d)可以看出:砂轮摆角主要分布在40°至50°。

图7 肥边修复打磨模式参数Fig. 7 Grinding pattern parameters of fat edge repair
针对钢轨肥边病害的4 种典型打磨模式,即:41&42 号、45&46 号、47&48 号(组合打磨模式)和49 号(单打磨模式),对图6 所示的筛选后钢轨廓形离散点进行NURBS 建模,将其作为算法初始模型,应用3.3 节所述的钢轨打磨模式优化决策算法,计算得到4种打磨模式下的钢轨打磨廓形质量指数及打磨模式优化决策排序,结果如表1 所示,可以看出47&48号为最优打磨模式。
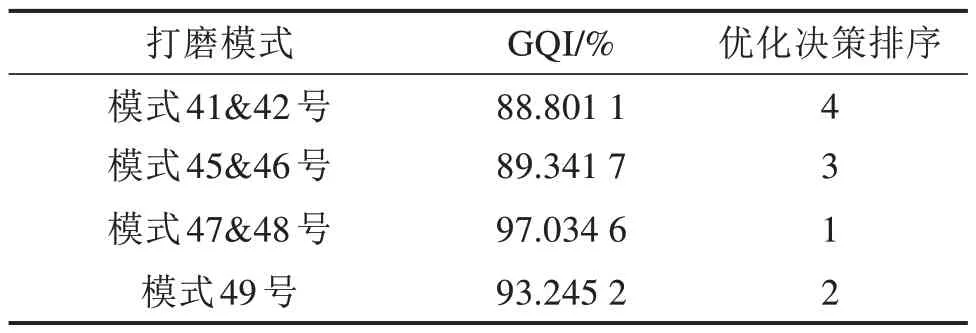
表1 不同打磨模式下钢轨打磨廓形质量指数Table 1 GQI in different grinding patterns
应用2.1和2.2节所述的方法,计算4种打磨模式下的钢轨打磨廓形与目标廓形的偏差并对其进行可视化,如图8所示,可以看出,肥边打磨模式下砂轮主要作用于钢轨轨头内侧,主要打磨偏差集中于廓形横坐标为[20, 36]区域,打磨模式47&48号对应的钢轨打磨廓形偏差最小。

图8 不同打磨模式下钢轨打磨廓形与目标廓形偏差图Fig. 8 Deviation diagram of rail grinding profile and target profile under different grinding patterns
分别采用以上4 种打磨模式进行钢轨打磨实验,并对打磨后的钢轨廓形进行检测,实验结果表明,采用打磨模式47&48 号的打磨廓形与打磨目标廓形最为接近,说明本文方法满足钢轨打磨的实际工程需求,从而实现钢轨打磨模式的最优决策。
4 结论
1) 提出一种基于NURBS 的钢轨打磨廓形质量指数的精确计算方法。采用NURBS 曲线拟合方法构建钢轨断面廓形参数模型,推导了GQI 求解函数关系,利用方向包围盒和区间迭代算法进行了精确求解。
2) 提取了打磨列车作用于钢轨时砂轮与钢轨廓形接触的数学关系,并依此设计了一种以砂轮摆角和打磨功率为变量的钢轨打磨廓形预测算法,实现了不同打磨模式下的钢轨打磨廓形预测。
3) 以GQI 为评判指标,设计一种钢轨打磨模式优化决策算法。通过构建钢轨打磨模式的寻优函数,结合钢轨打磨模式参数,应用NURBS 数值计算方法,实现了钢轨打磨模式的优化决策。
4) 进行钢轨打磨模式优化决策算法的实验验证。通过采集某区段肥边病害情况下的钢轨廓形数据,对4种打磨模式下的钢轨打磨廓形及GQI进行预测,并对打磨模式进行最优决策,验证了本文方法是切实可行的。
