基于DDPG算法的列车节能控制策略研究

2023-03-29武晓春金则灵

铁道科学与工程学报 2023年2期

武晓春，金则灵

(兰州交通大学自动化与电气工程学院，甘肃兰州 730070)

城市轨道交通已成为当今社会出行的重要方式，列车运行能耗是运营成本的重要组成部分，据统计2020年，城轨交通总电能耗172.4亿kW·h，其中，牵引能耗84 亿kW·h，占48.7%[1]。列车实际运行中的牵引能耗取决ATO 系统采用的控制策略。ATO 控制速度的过程可分为最优速度曲线的生成和速度控制部分2部分。最优速度曲线是根据列车参数和线路数据计算生成的最优速度曲线[2]，速度自动控制模块则根据计算出曲线控制列车输出连续牵引/制动力，实现速度的精确控制[3]。传统研究通常只考虑优化列车最优速度曲线或研究如何精确跟踪最优曲线，但在实际运行中，出现列车因牵引/制动性能变化或因供电问题等偏离预先计算出的最优速度，若离线计算方式难以满足实时性和精准性的要求。近年来，先进的人工智能技术不断进步，深度强化学习(Deep Reinforce Learning, DRL)是一种将强化学习的决策能力与深度学习的感知能力相结合的一种人工智能算法[4-5]，使用深度学习中的神经网络处理强化学习中的高维空间，使得深度强化学习能够克服环境的不确定性来逼近目标值。由于不需要准确的模型信息，提高系统的可扩展性，目前已经被用于处理许多不同领域的最优控制问题。MNIH 等[5]建立列车控制专家推理系统，采用基于策略的强化学习算法根据列车状态求解输出牵引-惰性组合速度的控制策略；张淼等[6]将线路划分为多个区段，采用DQN算法直接从牵引能耗角度求解满足运行时分要求的最优能耗分配方案；宿帅等[7]通过学习历史运行数据，提取专家知识规则并建立推理方法，提出了深度确定性策略梯度和归一化优势函数2种智能控车策略，最后验证算法的有效性和鲁棒性；赵立丹[8]建立了基于遗传粒子群算法和深度强化学习算法的列车节能优化模型，仿真验证智能算法相较于实际运行能耗，节能效果良好。以往深度强化学习算法的研究取得了巨大的成功，为复杂的列车自动驾驶控制提供了一种解决方案。目前多数研究未考虑列车运行过程中状态变化后实时调整控制策略。本文的主要目标是通过规划合理的牵引、制动、惰性和巡航列车控制策略使列车在满足运行要求的基础上减少牵引能耗，基于以上分析，本文采用DDPG 算法与城轨列车控制运行模型进行交互训练，将ATO速度控制2部分功能相结合，完成以下工作：1) 根据列车动力学方程组，建立列车仿真运行环境；2) 以Actor-Critic 框架作为DDPG 算法的主体，构建相应的神经网络结构，以安全运行、准点性、运行能耗和停车精度作为奖励函数，通过于仿真环境的交互，完成了对列车运行过程中控制策略的学习，实现对城轨列车运行的连续控制；3) 以长沙地铁2号线实际线路数据为例，与DQN 算法、动态规划算法进行对比验证算法的优越性，通过仿真运行中的列车临时调整进站时间和列车牵引系统故障，验证算法实时性和有效性。

1 构建列车运行模型

对列车运行过程进行准确描述是ATO 研究的基础，对城轨列车进行受力分析，根据牵引计算公式建立列车单质点动力学方程：

其中，M为列车质量；u为列车输出的牵引制动力；v为列车运行速度；R1(v)为列车运行阻力，与列车运行速度相关；a，b，c的值一般根据经验和不同的车型确定；R2为列车附加阻力，一般由坡道附加阻力wi，曲线附加阻力wr和隧道附加阻力ws组成，计算公式如式(2)所示。

其中，i表示列车当前位置坡道的千分数；R表示列车当前位置曲线半径；Ls表示当前位置隧道长度。

2 强化学习框架设计

深度强化学习算法使用强化学习来定义和优化目标，使用深度学习表征值函数和策略函数，列车与环境交互获取列车运行数据的过程可以简化为一个马尔科夫决策过程(MDPs)模型，如图1所示。

图1 MDPs模型Fig. 1 MDPs model

该模型主要由状态S，动作A，奖励R和策略μ这4 个部分组成。状态S表示列车当前的行车信息，不同的状态会对应不同动作策略；动作A表示列车输出的牵引制动力；奖励R表示与环境交互过程中对该动作的评价，引导智能体学习；策略μ表示列车根据当前状态采取的控制策略。

2.1 状态空间

在复杂运行环境下，为了准确描述列车当前信息，本文选择列车的速度，位置和剩余运行时间组成状态空间，定义为：

其中，xi和vi为当前时刻列车的位置和速度；Xend表示线路终点位置；Vlim表示线路最大允许速度；tr=Tplan-ti表示列车剩余可运行时间；Tplan为列车行程规划时间；ti为列车已运行时间。将列车运行过程离散为不同状态，列车运行的状态转移过程如图2所示。

图2 状态转移过程示意图Fig. 2 Schematic diagram of state transition process

为便于计算，本文采用行驶距离作为状态转移步长，根据列车实际情况，定义初始状态为s1=[0，0，Tplan]，结束状态为st=[Xend，0，Tplan-ti]。在状态转移过程中，根据公式(4)递推求得列车的速度v2和运行时间t2。

其中，v1和t1为列车上一时刻已知的速度和运行时间，dx为最小的距离单元。因线路长度不一定为距离步长的整倍数，若在最后一段步长中列车抵达线路终点，则将此时的距离和运行时间设置为结束状态。

2.2 动作空间

列车根据主控手柄或ATO 输出的连续模拟量产生相应的牵引或制动力控制列车运行[10]，因此本文动作空间A由列车的牵引/制动级位ki组成，如式(5)所示。

其中，Fmax和Bmax为列车最大牵引力和最大常用制动力，列车的牵引/制动级位范围为[-100%, 100%]，100%表示最大牵引力，-100%表示最大制动力，0%表示列车惰行。

2.3 奖赏机制设定

Agent 可根据定义的状态和动作，随机生成控制策略，通过不同的奖赏值引导算法学习更好的控制策略，使获得的回报最大。合理的奖惩机制能够提高收敛速度，通常情况下，形式化的奖励会比稀疏奖励更容易促进学习。本文根据ATO系统的功能，从安全性Rsafty，停车精度Rstop，准点性Rtime和节能性Remergy4个部分构建连续型奖励函数如式(6)所示，引导列车寻找最优控制策略。

1) 安全奖赏机制：城轨列车的运行安全由ATP进行防护，车载ATP根据移动授权、列车制动模型和实际参数计算紧急制动触发(Emergency Braking Intervention, EBI)曲线、全常用制动(Full Service Braking, FSB)曲线和速度告警(Warning)曲线，如图3所示。列车运行速度需始终低于全常用制动曲线速度，若超过该速度达到紧急制动触发曲线速度，ATP将立即输出紧急制动命令，在停车途中不得缓解，影响行车效率。列车在顶棚速度监督区运行时控制列车不超过各类固定限速的最小值，在速度-距离监督区域运行时，根据公式(7)实时计算最大允许运行速度。

图3 ATP曲线示意图Fig. 3 Schematic diagram of ATP curve

其中，slimit和vlimit表示距离列车前方最近限速点，如图3 中A的位置和速度。列车在制动阶段通常需要保持制动，若使用线路限速对列车进行奖赏判定，训练列车制动到停车点的学习效率很低，因此本文选用全常用制动曲线速度进行安全奖赏判定，如式(8)所示，当列车速度高于最大允许速度时，给予训练失败惩罚Rfail，同时触发终止条件。

2) 停车奖赏机制：根据文献[12]可知，为了保证列车门和站台屏蔽门在同一个位置打开，列车停车误差需要控制在0.3 m 之内，同时停车误差越小越好，定义停车奖赏机制如式(9)所示。

其中，Serror表示实际停车位置和屏蔽门之间的误差，在误差0.3 m 之内，离停车点越近获得的奖励越高，列车停车后触发终止条件，λ1为平衡权重系数。

3) 准点奖赏机制：准点运行是ATO 系统一个重要的功能[13]，若在列车到达后根据运行时间给定奖赏值，在运行过程中无法考虑到晚点的情况，会导致学习效率降低，本文定义准点奖赏机制如式(10)所示。

其中，Tmin为列车当前速度和位置采取最快驾驶策略需要的运行时间，当列车剩余运行时间少于该时间，表示列车不可避免会晚点，晚点越多惩罚越大，为了训练列车在不可避免晚点情况下的控制策略，列车出现晚点后依然训练至抵达终点后结束。

4) 能耗奖赏机制：在满足准点运行的情况下，尽可能的节约能耗是研究的主要问题，因此能耗是奖励函数主要组成部分，本文定义能耗奖赏机制如式(11)所示。

其中，C为大于两状态转移间最大能耗。从式(11)可以看出，两状态转移之间，列车运行牵引能耗越大，获得的奖励越少。

2.4 策略

列车在当前状态下选择一个动作执行称为策略μ，智能体选择当前状态下状态-动作函数Q值最大的动作，状态-动作函数Q定义为：

其中，γ表示折扣因子，γ越大表示更关注未来的回报，动作策略的累积回报值用函数J(μ)来表示，其定义为：

本文的目标是寻找一个控制策略，使J(μ)最大，即最优控制策略μ=argmaxμJ(μ)。

3 DDPG算法设计

DDPG 算法分为Actor-Critic 网络、回放经验池、列车运行模型以及奖励函数几个部分，训练过程如图4所示。Actor-Critic网络将列车状态和控制策略输出给列车运行模型模拟列车运行过程，奖励函数对动作策略进行评价，并奖励值和列车状态数据一起存入回放经验池中。采用经验回访机制，将样本存入经验池中，当经验池数据存满之后，小批量的随机采样样本训练Actor-Critic 网络，这样可以有效减少样本间的关联性，提高学习速度。

图4 DDPG算法框架Fig. 4 DDPG Algorithm Framework

强化学习的训练过程可以分为基于状态动作值函数更新和基于动作策略函数更新。Actor-Critic网络框架结合了值函数更新方式和策略函数更新方式两者的优势[14]，其中Critic 网络采用基于值函数单步更新的方式，用于评价列车当前控制策略的好坏，网络参数为θQ；Actor 网络采用基于策略梯度更新的方式，可以更好的解决连续动作空间的问题，用于输出列车控制策略，网路参数为θμ。

3.1 Critic网络

Critic 网络与深度Q 学习(Deep Q Network, DQN)算法相似，使用全连接神经网络拟合每一个状态动作值即Q(S，A|θQ)=Q(S，A)。将采样样本数据的状态观测量和动作作为输入，状态动作值Q作为输出，Q值越大表示该动作策略评价越高，采用式(14)～(16)计算神经网络参数新的权重。

其中，y＇t为目标值；αQ为学习率；∇Q(s，a|θQ t)为Critic 神经网络根据Q值计算出的更新梯度，输出给Actor 网络作为更新动作策略的依据，若梯度为正，表示最优策略向此控制策略靠近，梯度越大，靠近速度更快。

3.2 Actor网络

动作空间的划分对于强化学习影响很大，若空间太少，无法准确描述列车运动和操作过程；若划分空间过大，会导致维度过大，列车无法学习到所有动作，Actor 网络使用神经网络参数来近似估计列车控制策略，将采样样本数据的状态观测量作为输入，动作策略作为输出。根据策略的种类不同，可以分为随机性策略和确定性策略。随机性策略输出当前状态下选择不同动作的概率，即μθ(a|s)=P(a|s;θ)，该策略回报越大，对应概率越高；确定性策略输出当前状态下对应的最优动作，即a=μθ(s)。列车在运行过程中，每一种状态存在一个确定的最优控制策略，考虑列车运行中每一状态下存在最优控制策略，故本文选用确定性策略。根据梯度上升思想[15]对公式J(μ)求导,得到策略梯度的计算公式：

将随机采样的样本数据代入上述公式中作为期望值的无偏差估计，将式(17)进行改写得到策略梯度的计算公式(18)。

其中，s=si,a=μ(si)，神经网络参数的新权重计算公式：

3.3 网络参数更新及探索机制

为了增加算法训练的稳定性，减少神经网络大幅度的变化，Critic 网络和Actor 网络通过如式(20)～(21)所示的方式跟踪学习进行“软更新”而不是直接更改权重。

其中א表示OU 过程，根据列车实际运行情况，限制加入噪声后控制策略最大牵引级位不超过100%，最大制动级位不小于-100%。

4 验证与分析

为验证本文算法的有效性，以长沙地铁2号线6 编组B 型列车为例进行仿真验证，仿真列车参数如表1所示。

表1 仿真列车参数Table 1 Simulated train parameters

采用本文提出的DDPG 算法、DQN 算法和传统的动态规划算法分别进行仿真，DDPG 和DQN算法训练相关参数如表2所示，若在训练中触发章节2.3 中所述的终止条件，则停止当前的单次训练，重置列车为初始状态开始新的训练。DQN 算法使用离散的动作空间，因此需要先将动作离散化，本文将级位离散为[-100%，-80%，-60%，-40%，-20%，0%，20%，40%，60%，80%，100%]11个不同的操纵级位，离散数越多，训练难度也更大，在探索过程中增加噪声后，DQN 算法选取最接近的操纵级位。

表2 算法训练参数Table 2 Algorithm training parameter

如图5 所示为DDPG 算法和DQN 算法训练过程中每250次平均奖赏值变化过程曲线，横坐标为训练次数，纵坐标为平均回报值。

从图5 训练过程对比中可以看出DDPG 算法和DQN 算法平均奖赏值都上升后趋于稳定，DQN 离散的动作空间更容易学习，因此训练过程更加平稳，奖赏值稳定在6 左右小幅度震荡，DDPG 算法随着训练次数的增加，奖赏值一直在震荡上升，到达10后开始缓慢上升，训练结果如表3所示。

图5 DDPG和DQN算法训练过程对比Fig. 5 Comparison of training process of DDPG and DQN algorithm

表3 算法训练结果Table 3 Algorithm training result

由表3 可知，DDPG 算法比DQN 算法的状态转移次数更多，平均获得的奖励值更高，说明在50 000 次的训练中，DDPG 触发终止训练的次数更少，学习的效果更好。对完成训练后的智能体进行列车运行仿真模拟，仿真列车运行曲线如图6(a)所示，牵引/制动力级位曲线如图6(b)。

图6 仿真实验曲线Fig. 6 Simulation experimental curve

从图6(a)中可以看出3 种算法都满足限速的要求，出站后都加速至最大允许运行速度，随后利用线路的坡度调节列车运行速度，减少牵引能耗。从图6(b)中看出，DQN 算法加速到列车最大运行速度，在运行至200 m 左右切换为惰性工况，在第1 100 m 左右重新切换为牵引工况；动态规划算法列车进入巡航阶段后进行了多次速度调整，产生了更多的牵引能耗，随后利用进站前的上坡减速，避免了触发进站限速的制动；DDPG算法实时输出计算控制策略且使用无级控制，牵引力和制动力控制曲线更为平缓，在列车运行过程中，随着运行阻力的变化，不断调整输出的牵引力和制动力，使列车在运行过程中速度更为平稳。列车运行工况的频繁转换既会影响乘坐舒适度，也会影响牵引电机等设备的使用寿命，牵引/制动级位变化大时，还会放大部分列车控制指令跟随性延迟问题。对比3 种算法可以看出，DDPG 算法的工况转换次数更少且级位变化幅度更小，跟利于列车执行控制指令。仿真结果如表4所示。

通过表4 分析可知，DQN 算法晚点0.83 s 到达，动态规划算法和DDPG算法提前1.17 s和0.16 s，均满足3 s 之内的准点要求，距离停车点误差分别为0.2，0.21 和0.1 m，满足0.3 m 之内的停车精度要求。DDPG算法牵引能耗为18.25 kW·h，相较于DQN 算法减少了8.25%，相较于动态规划算法减少了21.7%，说明在该实验中DDPG 的节能控制训练效果最好，证明该算法的优越性。

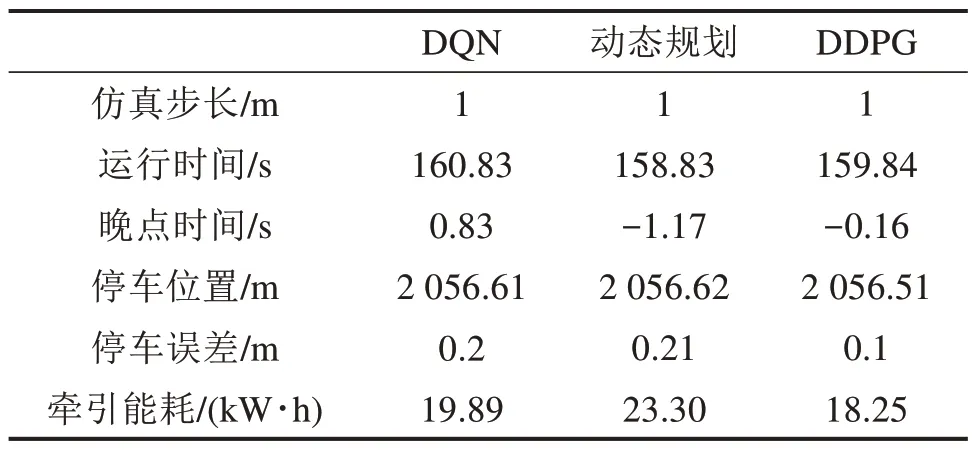
表4 仿真实验结果Table 4 Simulation results

状态转移步长是DDPG 算法训练中一个重要的参数，步长过长可能会错过最优解，步长过小会加大训练的难度，为使算法得到较好的优化效果，本文分别采用50，100，150 和200 m 的状态转移步长，其余训练参数保持不变进行仿真，得到实验结果如表5所示。

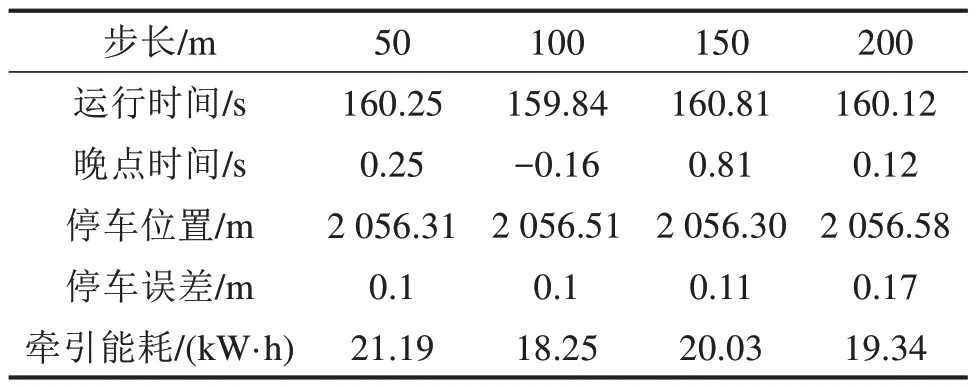
表5 不同状态转移步长实验结果Table 5 Results of different state transition steps

通过表5 分析可知，对于本文选取的线路数据，在训练50 000次后，状态转移步长为100 m 的DDPG 算法在满足准点运行和停车误差的情况下，牵引能耗最少。仿真曲线如图7所示。

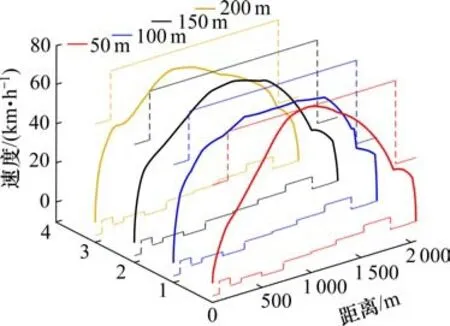
图7 不同状态转移步长仿真运行曲线Fig. 7 Simulation running curves of different state transition step

列车在区间运行过程中也会因前方车站出现事故，临时被通知需要调整进站的时间，这需要算法具有较好的鲁棒性来调整列车的控制策略，本文选取100 m 状态转移步长，其余参数不变，分别仿真在列车运行至500 m 处通知列车提前10s 到达下一车站和延后10 s 进站，得到实验结果如表6所示，仿真列车运行曲线如图8(a)所示，牵引/制动力级位曲线如图8(b)。

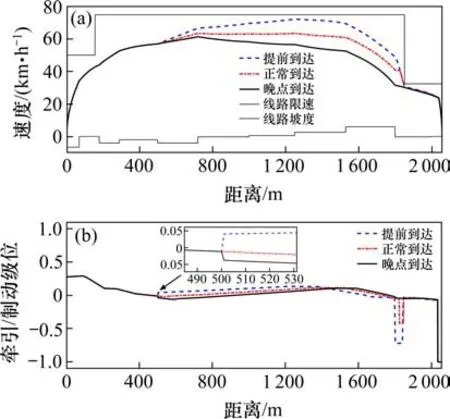
图8 仿真实验曲线Fig. 8 Simulation experimental curves

表6 临时调整进站时间实验结果Table 6 Results of temporary adjustment of arrival time

在通知列车调整进站时间信息后，列车的当前状态发生了变化，从图8(a)中可以观察到，列车分别采取了不同的控制策略调整列车运行速度。如图8(b)所示，接收到需要提前到达后，列车增加了4%的牵引级位，提高了运行的平均速度，相比正常运行，提前了8.17 s 到达；在通知列车延后到达后，列车输出了5%的制动级位，相比正常运行，延后了10.16 s到达，通过对表6分析可知，列车在运行过程中能根据实时的状态调整控制策略来完成运行目标，同时根据运行时间可以看出，提前10 s 和延后10 s 进站都在算法的调节范围内，在列车运行过程中减少剩余运行时间会需要列车输出牵引力提高运行速度，增加牵引能耗。

列车在区间运行过程中若出现牵引系统故障，会导致列车无法运行到目标速度，影响列车运行时间，这需要算法实时调整控制策略，使列车满足运行要求，本实验选取100 m 状态转移步长，其余参数不变，仿真在列车运行至100 m 处牵引系统故障，切除一个动力单元，其输出牵引力和制动力比原定减少25%，仿真结果如图9所示。

图9 牵引系统故障仿真运行曲线Fig. 9 Simulation running curves of traction system broke

从图9 中可以看出，在列车运行至100 m 时，由于牵引系统发生故障，列车输出同样的牵引级位产生的牵引力小于正常运行时产生的牵引力，导致列车的速度小于正常运行的列车。通过控制策略的调整，在列车运行至670 m 处，牵引故障列车运行速度超过正常运行列车，帮助追回由于速度减小损失的运行时间。牵引/制动力级位曲线如图10(a)所示，牵引/制动力大小如图10(b)所示。

图10 牵引系统故障仿真对比曲线Fig. 10 Simulation contrast curves of traction system broke

如图10 所示，算法根据列车在运行至100 m处反馈的当前运行状态，立即调整的控制策略，在列车运行至190 m 左右处输出的牵引级位大于正常运行的列车，使输出牵引力与正常运行相同，之后一直保持大于正常运行列车输出的牵引级位，牵引力都略大于正常运行的列车。在制动阶段，由于的制动力不足，算法输出更大的制动级位，产生的实际制动力与正常运行的列车相同，形成相同的制动效果，得到实验结果如表7所示。