指向深度学习的初中数学单元教学设计

彭恒仁

开展单元教学，应以引发学生深度学习、发展数学核心素养为目标，帮助学生获得“四基”、发展“四能”。下面，笔者以苏科版九年级下册“6.4探索相似三角形的条件”单元教学为例，浅析指向深度学习的初中数学单元整体教学设计与思考。

一、对单元内容的理解

从教材内容来看，苏科版“探索相似三角形的条件”中的内容安排在九年级下册第六章，其编排思路与八年级上册“全等三角形”的内容类似：也是由定义→性质→判定→应用。相似三角形和全等三角形之间是一种一般与特殊的关系，相似三角形的内容是全等三角形知识的进一步拓展与延伸，可以借助类比的思想引发从三角形的全等判定到相似判定（如图1）。

数学教学应该注重整体关联，基于数学的整体结构，利用知识、方法及探索路径之间的联系开展教学活动，让学生从已有的经验出发，在自主探索中自然建构，层层深入。为此，笔者因学设教，于全等三角形和相似三角形的知识关联处进行单元整体建构，以促进学生的深度学习。

二、教学目标

经历“观察—猜想—类比—验证—证明”的数学活动过程，理解相似三角形的概念，从概念出发分析两个三角形相似的条件，探索并证明相似三角形边和角的性质，并能在具体图形中找出相似三角形的对应边、角，写出比例式，进行相关的计算应用。

通过借助全等三角形研究相似三角形的过程，了解类比、转化思想方法，体会从特殊到一般的事物认知规律，明确研究图形和性质判定的一般思路。

三、教学过程设计

深度学习是素养目标达成的关键，对教师教学设计提出系列调整要求。而单元教学为深度学习提供了必要的知识和时空条件。基于以上分析，从单元教学视角出发，笔者对“探索相似三角形的条件”单元教学路径做了适当优化与调整，以促进学生的深度学习。

（一）回顾旧知，唤醒经验

问题1：全等三角形有哪些判定方法？

学生活动：回忆全等三角形的定义及全等三角形的判定方法。

追问1：全等三角形我们研究了哪些内容？

师生活动：两个三角形边和角的相等关系。

追问2：研究全等三角形的一般思路是什么？

学生活动：基于已有几何图形研究经验谈思路。

教师归纳：全等三角形的研究思路：“定义→性质→判定→应用”。

（设计意图：在学习之初，通过回顾全等三角形的研究内容及判定方法，同时梳理出研究两个图形之间关系的一般思路，从而为类比探究相似三角形的条件做好铺垫。）

（二）问题引领，获得概念

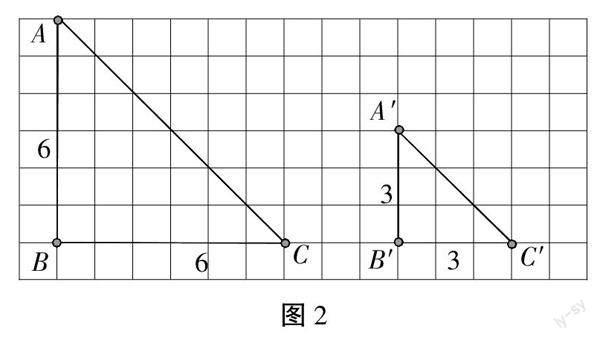
问题1：如图2，△ABC和△A′B′C′各个边、各个角之间有什么关系？

学生活动：利用格子图，首先观察到△ABC和△A′B′C′都为等腰直角三角形，且通过计算分析发现，两个三角形的对应角相等，其对应边有如下关系：AB=2A′B′，BC=2B′C′，AC=2A′C′，从而得出结论：△ABC和△A′B′C′形状相同，但大小不同。

问题2：如图3，△ABC和△A′B′C′各个边、各个角之间有什么关系？

追问1：两个三角形是否也有形状相同、大小不同的特点？

学生活动：首先从图形上来猜测，△ABC和△A′B′C′也具有形状相同、大小不同的特点，进一步通过计算验证两个三角形的各个对应角和对应边之间的关系，结果发现，它们的各个对应角相等，其对应边有如下关系：AB=2A′B′，BC=2B′C′，AC=2A′C′。

问题3：相似三角形的概念是什么？

学生活动：阅读教材内容，相似多边形的判定条件为各角分别相等，各边成比例，推出相似三角形的判定条件三角分别相等，三边成比例。

问题4：教材第50页例1，已知△ABC和△A′B′C′，求∠a的大小和A′C′的长。

学生活动：根据相似三角形的概念，得出两个三角形边与角的关系，进一步强化对概念的理解和运用。

（设计意图：引导学生从“边”和“角”要素出发研究两个三角形之间的关系，让学生掌握研究图形关系的关键要素，即“边”与“角”；在对问题1和问题2的探究中，学生得出初步結论和具有形状相同、大小不同的特点；通过例题的讲解，进一步深化学生对相似三角形概念的理解。）

（三）类比探究，获得定理

问题1：可不可以用比较少的条件来判定三角形相似呢？至少需要几个条件？

问题2：给出一个△ABC，如何画出一个与△ABC形状相同的△A′B′C′呢？

学生活动：自主学习，在刚开始探究过程中，主要有两种思路，一种思路是先画出一个角，使∠B′=∠B，然后再构造相似三角形；另一种思路是先画出一条边EF，由于是相似三角形，对应边成比例即可，所以对于EF的长度没有限制。

（设计意图：通过问题驱动的方式，促使学生主动思考，激发他们的探究欲望和学习积极性，在思考过程中，学生动手实践、观察，充分彰显了以生为本的教学理念。）

问题3：我刚看了很多同学都只画出了一个角或一条边，接着该怎么办呢？

追问1：你知道相似三角形的判定方法有哪些？

学生活动：判定两个三角形相似，需要知道它们的各角分别相等，各边成比例。

追问2：一定需要相似三角形定义中的全部条件吗？

追问3：两个三角形至少满足哪些条件就相似呢？由少到多分类说。

学生活动：一条边对应相等或一个角对应相等。

追问4：它们相似吗？请举出反例。

生：两个条件可以是两个角对应相等或者两边对应成比例。

追问5：三个条件的情况我们可以类比之前学过的什么内容呢？

生：三角形全等。

（设计意图：通过学习了相似多边形，让学生根据定义说出判定两个三角形相似需要满足哪些条件，激活学生的已有经验，并引导学生思考如何能用较少的条件判定，从而建立三角形相似与三角形全等的联系，形成从全等到相似类比探究的意识。）

問题4：你能结合三角形全等的相关知识，来思考我们下一步该如何构造相似△DEF吗？

追问1：首先我们看思路一，画出一个角，使∠B′=∠B，接下来呢？

学生活动：小组讨论，学生的思路主要有以下两种：一是再画出一个角，使∠C′=∠C，并且通过画图初步发现，对于一个三角形来说，如果两个角的大小确定了，即使大小没有确定，但形状已经基本确定了，也就是当两个三角形的两个角分别对应相等时，它们一定是相似的，在教师的指导下，进一步规范数学语言，从而引出三角形相似的判定定理1：两角分别相等的两个三角形相似。另一种思路是在画出∠B′=∠B后，可以画出类比三角形全等SAS的情况，画出该角的两边，结合相似三角形的概念，学生发现只要∠B和∠B′的两条夹边长度成比例即可。为验证该结论的正确性，让学生利用几何画板进行画图操作，由此引出三角形相似的判定定理2：两边成比例且夹角相等的两个三角形相似。

追问2：下面我们再来看之前画出一条边BC时，如何进一步画出一个与△ABC形状相同的△A′B′C′呢？

学生活动：有了前面的学习经验，通过类比思考，学生很快给出了两种解决方法：方法一是类比三角形全等ASA判定的方法，可以画出该边两端点的角，即使∠B′=∠B，∠C′=∠C，在此过程中，发现有两个角对应相等，两个三角形的形状基本已经确定，就可以直接用判定定理1。方法二是类比三角形全等SSS判定的方法，只要让△A′B′C′的对应边与△ABC的对应边成比例。

追问3：在△ABC和△A′B′C′中，如果满足ＡＢ／Ａ＇Ｂ＇=ＢＣ／Ｂ＇Ｃ＇=ＡＣ／Ａ＇Ｃ＇=k，那么能够判断这两个三角形相似吗？

学生活动：通过画图和度量初步猜测△ABC和△A′B′C′是相似三角形，进一步构造相似：△ADE∽△ABC，再证明△A′B′C′≌△ADE，最后推导出△ABC∽△A′B′C′。

教师总结：由此我们得到利用三边判定三角形相似的定理3：三边成比例的两个三角形相似。

（设计意图：通过观察、猜测、度量、作图等一系列数学活动，学生类比全等三角形的判定方法，推导出相似三角形的判定定理，在这一过程中，学生的逻辑推理能力、归纳总结能力得到很好的提升。）

（四）情境分析，概括性质

问题1：与三角形相关的要素有哪些？它们有什么关系？

追问1：除了边和角，还有其他要素吗？它们有什么关系？

师生活动：学生独立思考，从边、角想到三角形的高、中线及角平分线等，形成研究几何图形的一般思路。

问题2：已知△ABC，现按照1：2的比例建造△A′B′C′，分别过A点、A′点向对边作三角形的高，分别为AD、A′D′，那么△BCD和△B′C′D′相似吗？为什么？如果相似，指出它们的相似比。

（设计意图：让学生回顾证明三角形相似的方法，积累研究相似三角形对应高的关系的经验。）

问题3：按照刚刚研究相似三角形对应高的方法，你能猜想出其他结论吗？

追问2：你能用一句话概括上述结论吗？

师生活动：对比高的探索方法，学生先独立思考，然后对角平分线、中位线等方面进行探索，得出结论相似三角形的对应线段的比等于相似比。

四、教学反思

本节课设计较为成功之处主要有以下两点：一是通过复习全等三角形的判定方法，类比猜想能否证明三角形相似，学生迅速完成由旧知向新知的转化，激发了学生的探究兴趣。二是在探究判定的证明过程中，学生采用动手实践、自主探索与合作交流的学习方法，在教师的引导下从直观感受的层次上升到理性层次的认识，进一步发展学生合情推理能力。

编辑：曾彦慧