内置工字钢圆端形钢管混凝土短柱局压性能的有限元分析

谢晋，李兵

(沈阳建筑大学土木工程学院，沈阳 110168)

考虑到桥墩结构中多应用圆端形作为桥墩的外形，以利用其抗冲击、强弱轴特性，同时钢管混凝土结构作为较为完善的混凝土柱体改进方式，在土木结构领域中广泛应用。故对于圆端形钢管混凝土柱的性能研究是桥梁领域研究中不可缺少的一部分。桥墩所受外力为桥梁支座传递的局压荷载作用，故研究圆端形钢管混凝土柱的局压性能是极为重要的。随着土木工程领域的不断进步[1-5]，结构设计逐渐向高强度、高性能方向发展，故研究钢管混凝土柱[6]的强化方式是该领域发展的重要一环。

在现阶段研究中，李兵等[7]主要研究不同加载方式下圆端形钢管混凝土短柱的应力变化情况。沈奇罕等[8]主要研究圆端形钢管混凝土短柱的局压性能。任志刚等[9-10]主要研究圆端形钢管混凝土短柱的极限承载力计算方法与偏压截面优化。但上述研究都缺少对该种柱强化方式的研究。王传贻等[11]主要研究装配式钢骨-混凝土组合柱的抗震性能。尹朝正等[12]主要研究轴压荷载作用下钢骨混凝土组合短柱性能。周天华等[13]主要研究单轴对称十字型钢中长柱的偏压性能，上述研究中对钢骨混凝土的研究较为充分，同时也从侧面证明了钢骨混凝土具有良好使用性能，但现阶段对钢骨混凝土与圆端形钢管混凝土相结合的研究较少。

考虑到钢骨混凝土在相应研究中表现出的实用性，现研究工字钢强化圆端形钢管混凝土短柱[14]方法的可行性，工字钢参数变化对内置工字钢圆端形钢管混凝土短柱局压性能影响，并研究其相关性能。

1 有限元分析模型

1.1 有限元模型参数

内置工字钢圆端形钢管混凝土短柱截面示意图如图1所示。将内置工字钢圆端形钢管混凝土短柱分为纵向放置工字钢和横向放置工字钢两种情况进行分析。

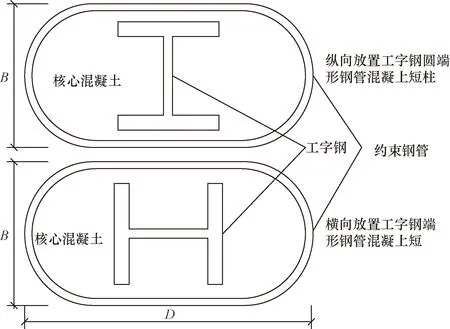
B为柱截面宽度；D为柱截面长度图1 内置工字钢圆端形钢管混凝土短柱截面示意图Fig.1 Section diagram of CECFST short column with built-in I-steel

建立的有限元模型参数表如表1所示。主要研究考虑工字钢参数如下：工字钢放置方向为纵向放置工字钢(ZG)和横向放置工字钢(HG)，工字钢高度(GD)为25、50、75、100、125 mm，工字钢宽度(KD)为25、50、75、100、125 mm，工字钢翼缘厚度(YH)为10、15、20、25、30 mm，工字钢腹板厚度(FH)为10、15、20、25、30 mm。

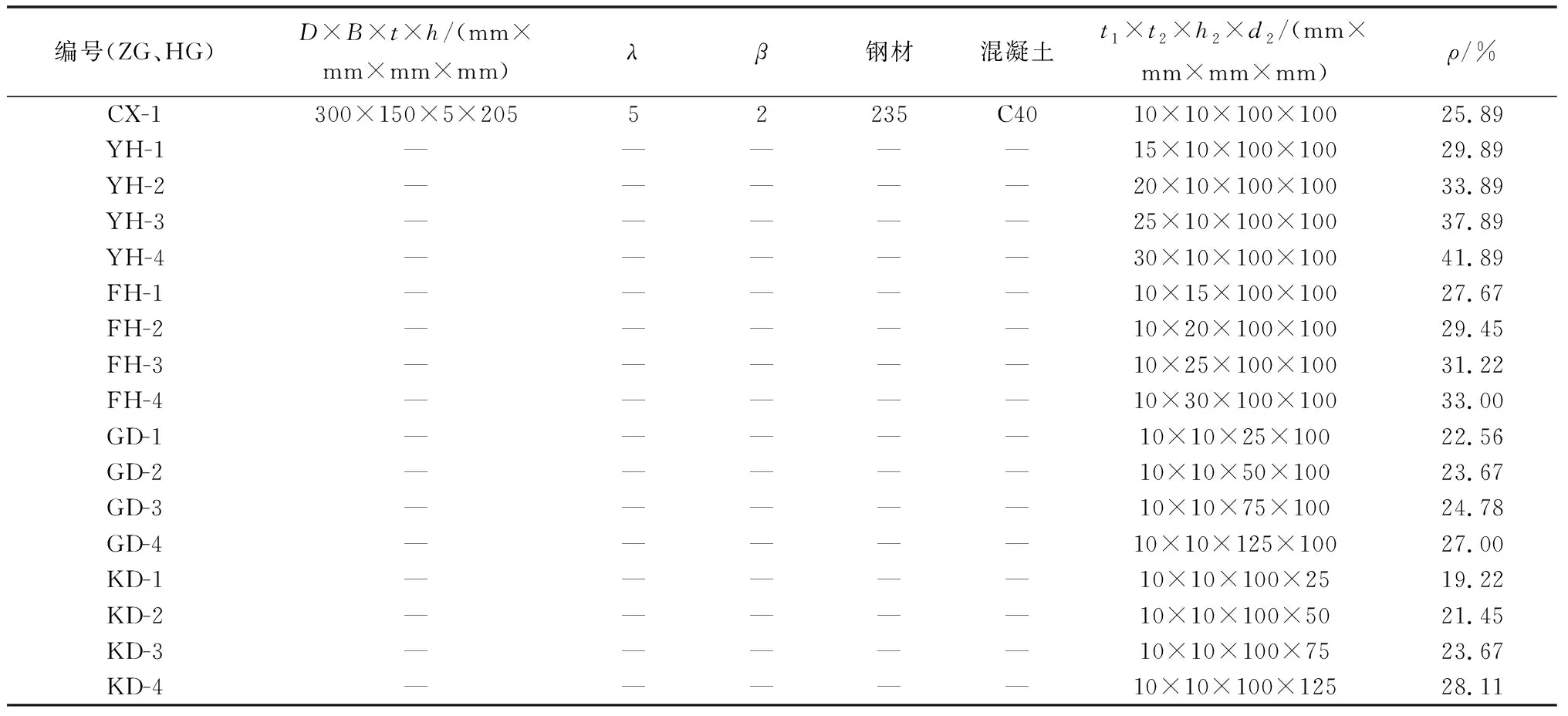
表1 有限元模型参数表Table 1 Parameters of finite element model

1.2 材料本构模型及有限元模型建模过程

有限元模型涉及钢材与混凝土，钢材本构关系使用二次塑流模型，其具体公式见文献[15]。根据长宽比β不同，将混凝土本构关系分别等效为圆形与矩形钢管混凝土柱混凝土本构关系，其具体公式见文献[16]。有限元模型各部分均采用C3D8R实体单元进行建模，有限元模型及网格划分示意图如图2所示。工字钢单元格密度为7，混凝土单元格密度为13，钢管单元格密度为17。

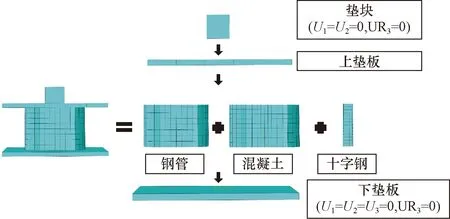
U1为X轴方向平移自由度；U2为Y轴方向平移自由度；U3为Z轴方向平移自由度；UR3为Z轴方向旋转自由度图2 有限元模型及网格划分示意图Fig.2 Schematic diagram of finite element model and meshing

混凝土与工字钢、钢管之间的接触关系分别设定为法向、切向两种行为，并各自设置为硬接触、罚。根据文献[16]，罚摩擦因数[17]设为0.3。柱底端采用铰接约束，顶部采用固定滑轮约束，为实现局压荷载作用，在柱顶端设置正方形垫块，垫块面积根据局压面积比进行设置，其具体计算公式见文献[17]，局压面积比(Г)设置为4。

1.3 有限元模型的验证

为验证有限元模型准确，取文献[18]圆端形钢管混凝土短柱试验结果与有限元计算结果进行比较，其对比结果如表2所示。N-μm曲线对比图如图3所示。N为施加于试件上的荷载，μm为对应的位移值。

表2 文献[18]试验结果与有限元结果对比表Table 2 Comparison of test results and finite element results in reference[18]

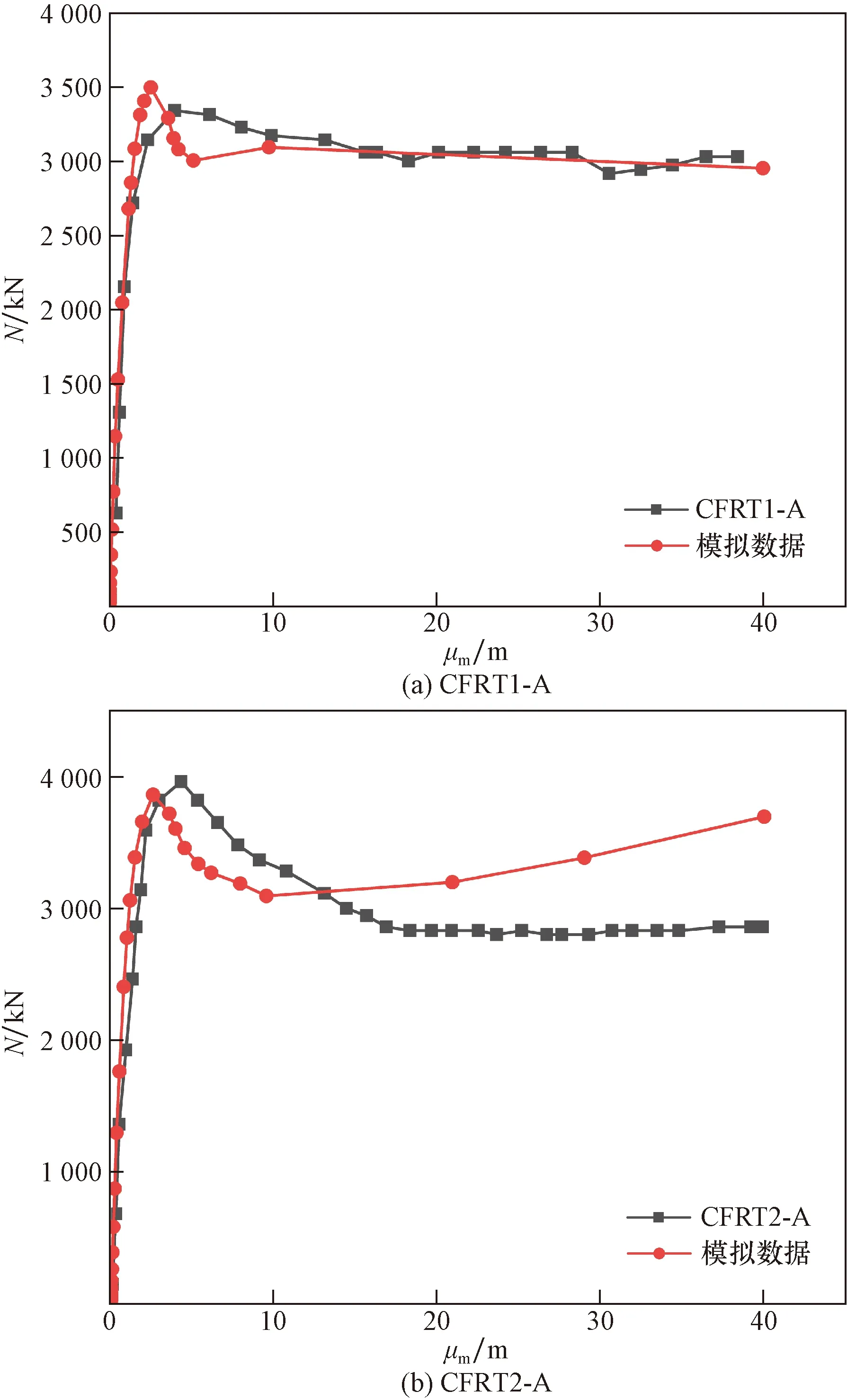
图3 文献[18]试验与有限元模型N-μm曲线对比Fig.3 Reference[18] test and finite element model N-μm curve comparison

结果表明，试验结果与有限元计算的N-μm曲线基本吻合，有限元计算承载力与试验承载力平均比值为1.03，可知有限元模型建立准确。

2 参数分析

研究参数的N-μm曲线如图4、图5所示。

图4 不同工字钢参数下N-μm曲线(ZG)Fig.4 Different I-steel parameters N-μm curve (ZG)

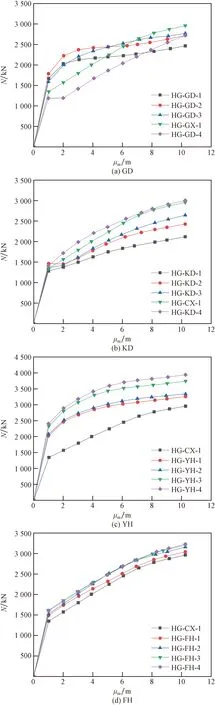
图5 不同工字钢参数下N-μm曲线(HG)Fig.5 Different I-steel parameters N-μm curve (HG)

2.1 工字钢高度

由图4(a)与图5(a)分析可知，当ZG时，承载力最高试件为ZG-CX-1，承载力为2 992 kN，承载力最低试件为ZG-GD-1，其承载力为2 244 kN。当工字钢高度由25 mm变为50 mm时，承载力上升8.29%，由50 mm变为75 mm时，承载力上升7.20%，由75 mm变为100 mm时，承载力上升14.86%，由100 mm变为125 mm时，承载力下降8.32%。

当HG时，承载力最高试件为HG-CX-1，承载力为2 958 kN，承载力最低试件为HG-GD-1，承载力为2 465 kN。工字钢高度由25 mm变为50 mm时，承载力上升10.34%，由50 mm变为75 mm时，承载力上升1.91%，由75 mm变为100 mm时，承载力上升6.79%，由100 mm变为125 mm时，承载力下降7.27%。

2.2 工字钢宽度

由图4(b)与图5(b)分析可知，当ZG时，承载力最高试件为ZG-KD-4，承载力为3 011 kN，承载力最低试件为ZG-KD-1，承载力为2 402 kN。工字钢宽度由25 mm变为50 mm时，承载力上升13.78%，由50 mm变为75 mm时，承载力上升2.56%，由75 mm变为100 mm时，承载力上升6.74%，由100 mm变为125 mm时，承载力上升0.64%。

当HG时，承载力最高试件为HG-KD-4，承载力为3 006 kN，承载力最低试件为HG-KD-1，承载力为2 119 kN。工字钢宽度由25 mm变为50 mm时，承载力上升14.58%，由50 mm变为75 mm时，其承载力上升8.98%，由75 mm变为100 mm时，其承载力上升11.79%，由100 mm变为125 mm时，其承载力上升1.62%。

2.3 工字钢翼缘厚度

由图4(c)与图5(c)分析可知，当ZG时，承载力最高试件为ZG-YH-4，承载力为3 943 kN，承载力最低试件为ZG-CX-1，承载力为2 992 kN。工字钢翼缘由10 mm变为15 mm时，承载力上升8.96%，由15 mm变为20 mm时，承载力上升2.55%，由20 mm变为25 mm时，承载力上升12.03%，由25 mm变为30 mm时，承载力上升5.29%。

当HG时，承载力最高试件为HG-YH-4，承载力为4 163 kN，承载力最低试件为HG-CX-1，承载力为2 958 kN。工字钢翼缘由10 mm变为15 mm时，承载力上升15.55%，由15 mm变为20 mm时，承载力上升4.45%，由20 mm变为25 mm时，承载力上升10.31%，由25 mm变为30 mm时，承载力上升5.71%。

2.4 工字钢腹板厚度

由图4(d)与图5(d)分析可知，当ZG时，承载力最高试件为ZG-FH-4，承载力为3 673 kN，承载力最低试件为ZG-CX-1，承载力为2 992 kN。工字钢腹板由10 mm变为15 mm时，承载力上升5.41%，由15 mm变为20 mm时，承载力上升6.06%，由20 mm变为25 mm时，承载力上升5.05%，由25 mm变为30 mm时，承载力上升4.52%。

当HG时，承载力最高试件为HG-FH-4，承载力为3 227 kN，承载力最低试件为HG-CX-1，承载力为2 958 kN。工字钢腹板由10 mm变为15 mm时，其承载力上升2.67%，由15 mm变为20 mm时，承载力上升3.89%，由20 mm变为25 mm时，承载力上升1.43%，由25 mm变为30 mm时，承载力上升0.84%。

模拟过程中，当工字钢高度超过100 mm时，承载力出现下降，且HG与ZG两种情况皆出现该种情况，分析其原因为，当工字钢高度超过100 mm后，工字钢翼缘部分完全脱离局压加载区域，在这种情况下，翼缘部分不能完全承受外力作用，其示意图如图6所示。

图6 工字钢高度超过100 mm承载力下降情况示意图Fig.6 Schematic diagram of bearing capacity decline of I-steel with height exceeding 100 mm

2.5 工字钢放置方向对比

以ρ为基准对比不同工字钢参数对局压承载力的影响，并对比出该种情况下对承载力影响较大的参数，曲线如图7所示。

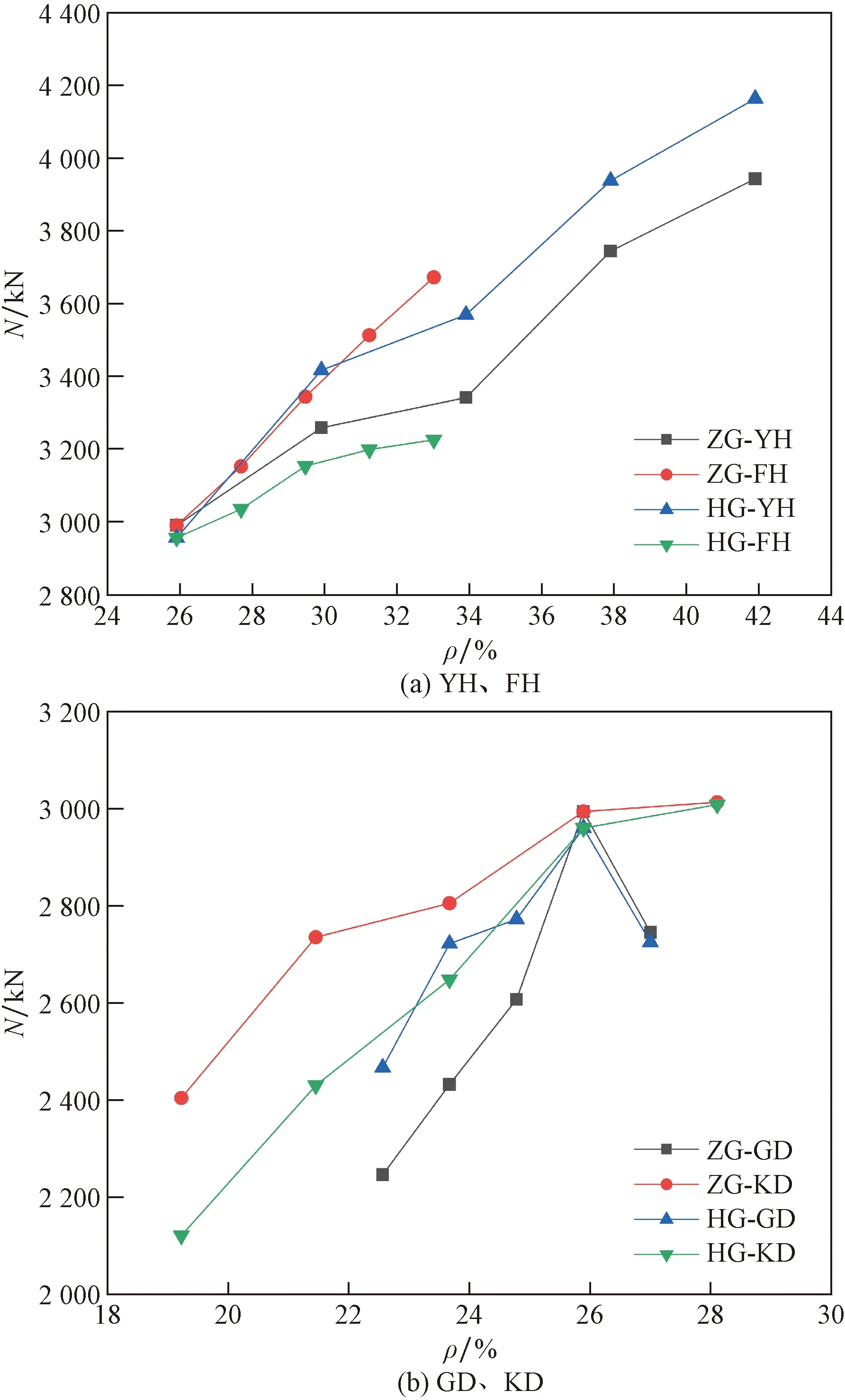
图7 不同ρ圆端形钢管混凝土短柱承载力对比图Fig.7 Performance comparison diagram of different ρ of CECFST

由图7(a)分析可知，对比工字钢翼缘厚度与腹板厚度参数变化对局压承载力的影响，当ρ<34%时，ZG-FH参数变化对局压承载力影响较大。当ρ>34%时，HG-YH参数变化对局压承载力影响较大。

由图7(b)分析可知，对比工字钢高度与工字钢宽度参数变化对局压承载力的影响，ZG-KD参数变化对局压承载力强化较大。

3 破坏模态分析

通过对试件ZG-CX-1的应力云图进行分析，得出该种情况下柱的破坏模态，应力云图如图8所示。

图8 局压荷载作用下圆端形钢管混凝土短柱破坏模态 Fig.8 Failure modes of CECFST short columns under local compressive load

由图8可知，局压荷载作用下圆端形钢管混凝土短柱破坏模态主要表现为：垫块加载位置混凝土出现凹陷；在垫块加载位置外的混凝土，因局压荷载作用而与钢管发生脱离。外钢管加载端部凸起，且其加载端纵向位置钢管凸起最为严重。

4 局压承载力计算公式

内置工字钢圆端形钢管混凝土短柱局压承载力计算公式参考文献如下：①文献[8]，研究的圆端形椭圆钢管混凝土短柱承载力计算公式；②文献[16]，研究的圆端形椭圆钢管混凝土的轴压性能；③文献[19]和文献[20]，对内置型钢的钢管混凝土柱承载力计算公式的研究。

同时，在上述研究基础上，考虑内置型钢、工字钢放置方向及工字钢高度对局压承载力的影响，其具体公式为

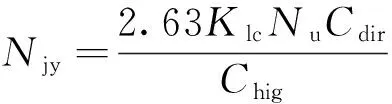
(1)

式(1)中：Njy为内置工字钢圆端形钢管混凝土短柱局压承载力；Klc为局压折减系数；Nu为内置工字钢圆端形钢管混凝土短柱承载力；Cdir为工字钢放置方向影响系数；Chig为工字钢高度影响系数。

Klc=(A3Γ+B3Γ0.5+C3)/f(β)

(2)

式(2)中：A3、B3、C3、f(β)分别为局压折减系数计算系数1、2、3、4。

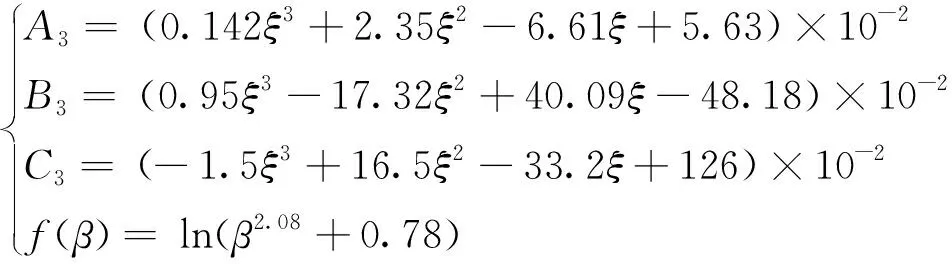
(3)

式(3)中：ξ为圆端形椭圆钢管混凝土约束效应系数。

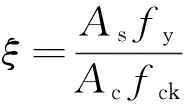
(4)

式(4)中：As为圆端形钢管截面面积；fy为钢管屈服强度；Ac为混凝土截面面积；fck为混凝土轴心抗压强度标准值。

Nu=Ascfscy+Agsfgsd

(5)

式(5)中：Asc为圆端形钢管混凝土短柱全截面面积；fscy为圆端形钢管混凝土短柱统一强度；Ags为工字钢截面面积；fgsd为工字钢屈服强度。

(6)

通过所提出的局压承载力公式计算承载力与模拟结果对比结果如表3所示。

由表3对比结果可知，本文公式计算承载力与模拟承载力比值区间为0.86～1.06，误差小于10%，计算结果较准确，可以应用于承载力计算。

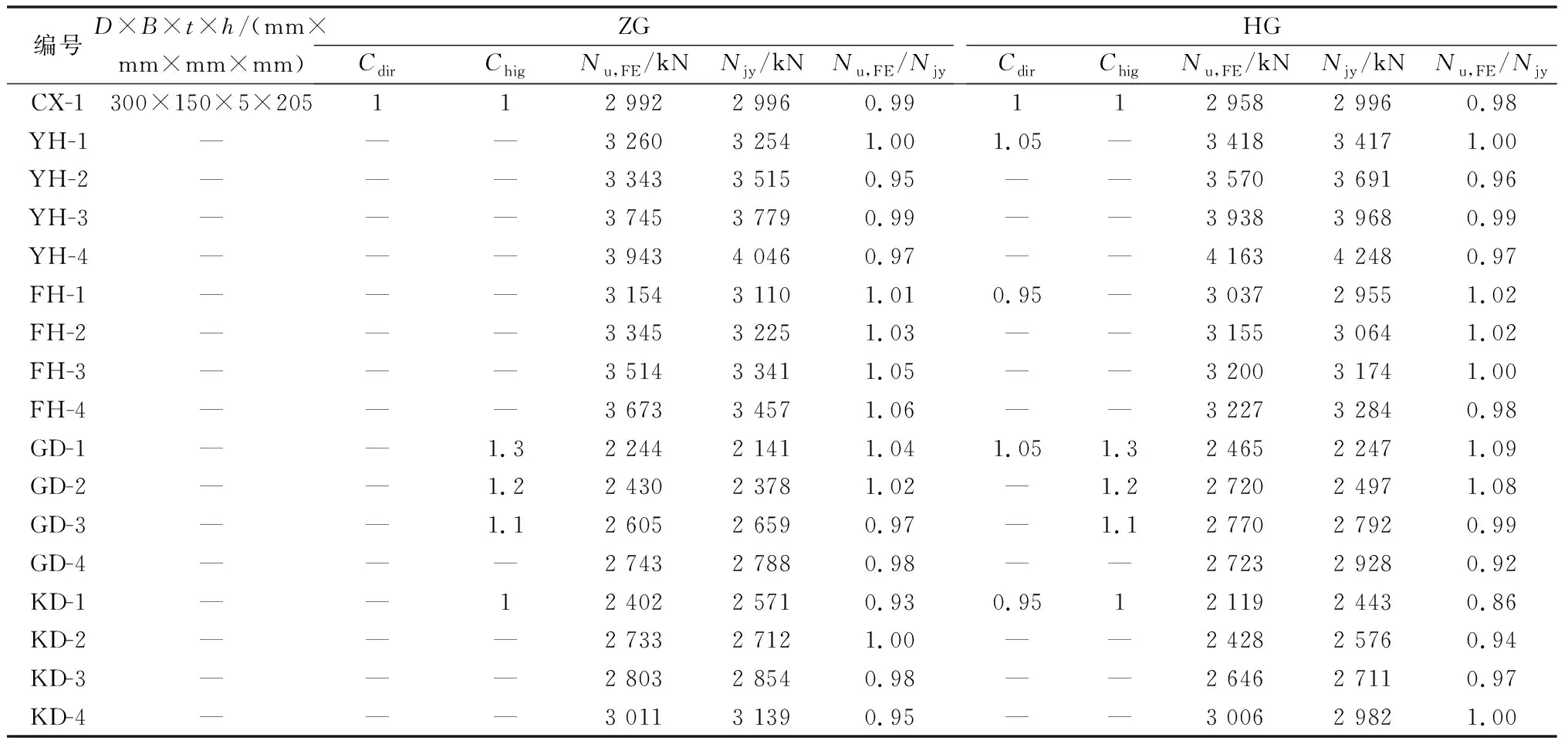
表3 模拟承载力、计算承载力对比表Table 3 Comparison of simulated bearing capacity and calculated bearing capacity

5 结论

(1)当ρ<34%时，ZG-FH参数变化对局压承载力影响较大；当ρ>34%时，HG-YH参数变化对局压承载力影响较大。对比工字钢高度与工字钢宽度变化对局压承载力的影响，ZG-KD参数变化对局压承载力影响较大。

(2)使用工字钢强化圆端形钢管混凝土短柱局压性能时，若工字钢超出垫块加载位置，承载力下降，分析其原因为，对局压性能的强化中，对加载区域进行强化的效果明显强于对加载区域外进行强化。

(3)局压荷载作用下圆端形钢管混凝土短柱破坏模态为，垫块加载位置混凝土凹陷，垫块加载位置外混凝土与钢管发生脱离，外钢管加载端纵向位置钢管凸起严重，加载位置工字钢变形严重。

(4)根据前人研究提出内置工字钢圆端形钢管混凝土短柱局压承载力计算公式，并使用所提公式与模拟结果进行验证，所提公式计算承载力与模拟承载力比值为0.86～1.06，误差小于10%，计算结果较为准确，可以用于承载力计算，并为相关的研究提供依据。