双折线卷筒端板受力分析及应用

刘须军

中船第九设计研究院工程有限公司 上海 200090

0 引言

随着各种大扬程起重设备需求的快速增加，多层缠绕卷筒的应用也越来越多。双折线卷筒解决了多层卷绕钢丝绳的排绳问题，提高钢丝绳的使用寿命，在工程中得到广泛应用。由于双折线卷筒钢丝绳缠绕过程中的挤压力以及向新一层过渡过程中的楔入作用，各层钢丝绳的直线段和折线段均对卷筒端部侧板有轴向推力。在轴向推力的作用下，端部侧板将产生较大应力，且随着层数的增加应力也随之增加，特别是超过5层及以上的双折线卷筒。由于端板的折线段接触区域应力远高于直线段接触区域，且受力不对称，卷筒端板可能出现扭曲变形，在卷筒侧端板根部严重时会出现开裂甚至断裂[1]。由于卷筒上的受力复杂，对于轴向推力的计算，目前国内基本上采用传统的经验公式法，由于与实际受力不同，有可能造成双折线卷筒端部侧板的设计达不到理想效果。在2008年挪威船级社（Det Norske Veritas，DNV）标准还因端板断裂而专门进行了修订，对双折线卷筒缠绕超过5层及以上的安全系数由1.75提高至3，这对很多在用双折线卷筒显得过于保守。因此，准确计算端部侧板受力合理设计端板结构，对双折线卷筒设计的具有现实意义。

本文对钢丝绳缠绕过程中的挤压力进行分析，分别得出双折线卷筒端板在直线段、折线段的轴向受力。利用Matlab和有限元技术计算端板的结构应力和变形，根据计算的结果与卷筒传统计算方法进行比较，通过对影响计算结果的各因素进行综合分析，为提高双折线卷筒设计的安全性和可靠性提供有益参考。

1 双折线卷筒端部侧板应力分析

1.1 卷筒受力

卷筒承受的载荷主要有钢丝绳缠绕产生的作用于卷筒壁上的缠绕压力p(x)，以及作用于卷筒两侧端板上的轴向推力Npi、Nai如图1所示。双折线卷筒的钢丝绳在缠绕过程中做空间螺旋运动，其在直线段、折线段对端板的轴向推力不同，且卷筒两侧端板受力不对称。钢丝绳与端板之间及钢丝绳之间有摩擦力，同时假定卷筒筒体为均匀受压，端部挡板依据钢丝绳与端板接触区按折线段和直线段均布线载荷。钢丝绳以一定的张力缠绕，并在缠绕过程中对卷筒表面产生径向压力以及对卷筒两端侧板产生轴向推力，这些是引起卷筒破坏的主要外力。

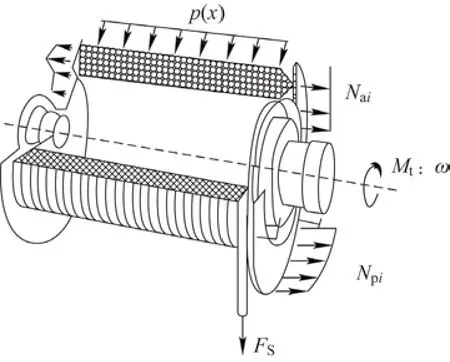
图1 卷筒受力示意图

1.2 卷筒端板常规受力计算

齐治国等[2]通过试验研究推算出端板轴向推力公式并在行业得到应用。

式中：S为钢丝绳额定拉力；n为钢丝绳缠绕层数；e为自然对数的底，e=2.718。

为了简化计算假设轴向压力在侧板上均布处理，引用薄板理论中受对称均布载荷的圆板计算公式，即卷筒侧端板根部弯曲强度

式中：H为卷筒端板的计算高度，C为与卷筒材料和尺寸有关的系数，q为端侧板上的均布压力，h为端板厚度。

当泊松比μ=0.3时，相应的C值如表1所示。

表1 泊松比μ=0.3时相应的C值

为了简化计算，假设端板所受轴向压力按钢丝绳层均布线载荷，在端板径向方向载荷根据不同钢丝绳层而相应变化。

1.3 卷筒端板理论受力计算[3]

钢丝绳在双折线卷筒缠绕过程中与端板的接触由2部分组成，即直线区和折线区，其中折线区是钢丝绳在端部折返换层过程区域。同时假设钢丝绳截面是圆形，端板与卷筒垂直。

根据力的平衡，换层折线段（见图2）端板轴向力为

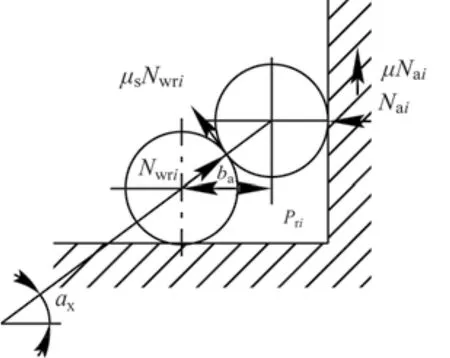
图2 端板受力示意图

式中：Pri为单位长度上钢丝绳的径向压力。

折线段钢丝绳对端板平均线性轴向力为

直线段钢丝绳对端板平均线性轴向力为

式中：Si为i层钢丝绳张力，Ri为i层缠绕半径，θz为折线段对应的圆心角，θp为直线段对应的圆心角，μ为钢丝绳与端板间滑动摩擦系数，μs为钢丝绳与钢丝绳间滑动摩擦系数，d为钢丝绳直径，t为节距。

2 端板受力计算约束

根据双折线卷筒钢丝绳缠绕的特性，端板与钢丝绳接触区是不对称的，即每层钢丝绳与端板接触区域只有一个折线段和直线段，紧邻一层为另一折线段和直线段与端板接触，也就是每一层端板轴向受力区域最多有一半，且相邻缠绕层对端板轴向受力不在同一区域位置。图3是端板受力有限元计算云图，折线段和直线段受力不均匀，且在折线区和直线区之间，由于钢丝绳换层时钢丝绳出现交叉过度，钢丝绳对端板产生斜楔力而引起轴向力增加，不对称轴向应力严重影响端板的应力分布，特别是对于层数超过5层的多层缠绕卷筒端板，严重的将造成端板翘曲变形甚至根部撕裂；同时钢丝绳在缠绕过程中，特别是在换层过程中对端板有挤压磨损，在此阶段的损伤是导致钢丝绳断丝的主要原因[5]。为了验证双折线缠绕方式对卷筒端板的轴向作用力，文献[6]进行了实验研究。图4为多层缠绕卷筒端板受力试验情况，由图可知，钢丝绳换层交叉区域应力远高于直线区域，且应力在换层开始急剧增加。

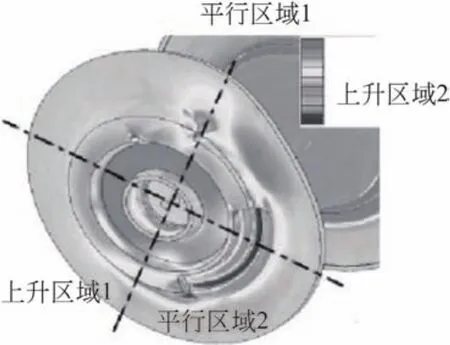
图3 端板受力有限元计算云图

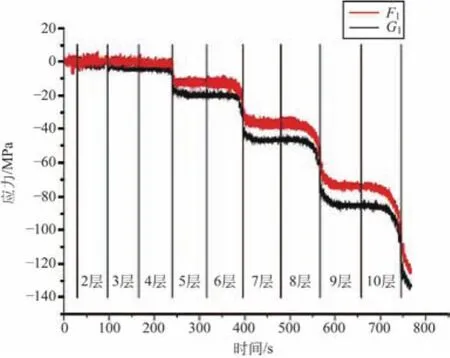
图4 端板F1、G1位置应力曲线

计算端板受力时有国内文献假设将端板推力简化为沿某一圆周方向作用的均布线载荷，其大小在圆周方向上为常量，径向方向为变量。本次为更精确计算端板受力，并方便利用有限元计算软件计算端板应力和变形情况做如下处理：1）折线段和直线段按理论接触区均布线载荷进行计算，并分别统计每层与端板理论接触的直线段和折线段受力；2）端板为内周边固定、外周边自由的弹性圆板；3）忽略受载后筒壁变形对端板的影响；4）忽略钢丝绳与端板之间为引导钢丝绳规则排列而设置的引导镶嵌条的影响。

然后利用Matlab软件采用式（1）、式（2）分别计算出每层直线段和折线段与端板接触处的均布线载荷，最后根据双折线卷筒的实体建模利用I-IDEAS软件对端板受力情况进行应力和变形计算。

3 端板受力实例计算和应用分析

本文采用文献[3]中的1组双折线卷筒参数计算该卷筒在缠绕8层钢丝绳后其端板的受力情况，同时进行有限元计算和分析并与传统方法计算进行数据对比。根据影响计算结果的各主要因素进行综合分析评判，给出影响结果并提出建议以便在实际应用中参考。双折线卷筒结构的主要技术参数为：钢丝绳静拉力Smax=30 kN，钢丝绳直径dmin=20 mm，缠绕层数n=8，卷筒壁厚δ=45 mm，卷筒底径D0=600 mm，端板高度H=175 mm，端板厚度h=20 mm，节距P=21 mm。

传统计算该卷筒端板受轴向力及最大应力为

本例双折线卷筒折线段对应中心角45°、直线段对应中心角135°，钢丝绳间摩擦系数µs取0.16，钢丝绳与端板摩擦系数µ取0.16。双折线卷筒在多层缠绕过程中每层钢丝绳的张力都在不断变化，为了得到每层钢丝绳准确的张力，文献[3]利用Matlab分别计算在缠绕8圈后各层钢丝绳的张力，如图5所示。

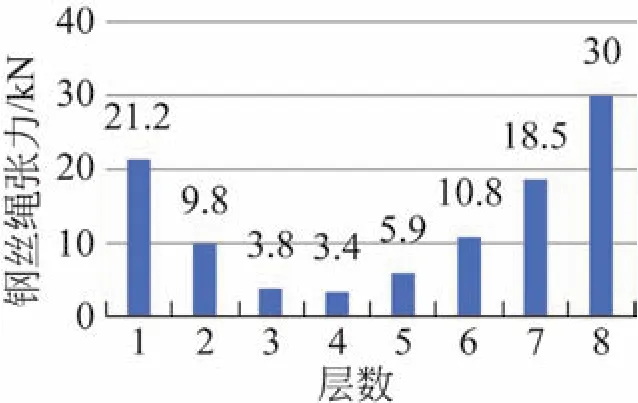
图5 各层钢丝绳张力

根据以上各层钢丝绳的张力，使用式（1）、式（2），利用Matlab软件分别对双折线卷筒各层缠绕钢丝绳的直线段，换层爬升折线段对端板的轴向推力进行详细计算，如图6所示，折线区单位受力比直线区较大，其中折线段弧长仅有直线段弧长的1/4，每层钢丝绳仅有一半与端板直接接触，计算所得端板总受力为204.6 kN，比传统方法计算减少约20%。传统方法计算不考虑钢丝绳之间以及钢丝绳与端板之间的摩擦系数。但在实际应用过程，要求钢丝绳应有良好的润滑以减少钢丝绳之间及钢丝绳与端板之间的滑动摩擦磨损。本文计算显示，钢丝绳与端板之间摩擦系数降低将使钢丝绳对端板的压力增加。

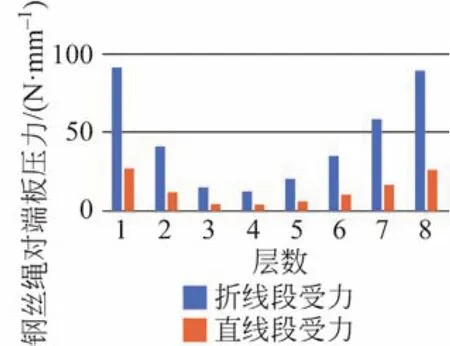
图6 各层钢丝绳对端板压力

将轴向力计算结果用I-IDEAS进行实体建模的端板应力和应变计算，如图7所示。结果显示，在卷筒侧端板根部折线段出现最大应力σmax=328 MPa，相应外侧应力σmax=223 MPa，端板最外缘最大变形量为δmax=1.46 mm；而相位差90°的直线段卷筒侧端板根部应力σmax=111 MPa，相应外侧σmax=77 MPa。

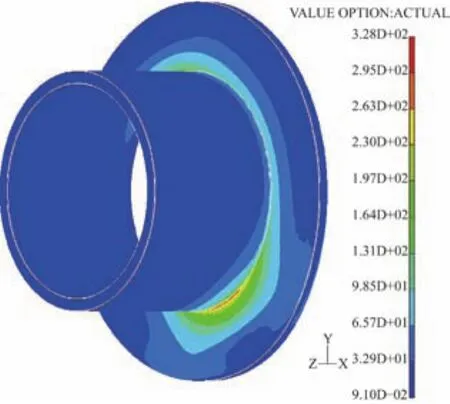
图7 端板V应力云图

本次采用实体建模，最大应力出现在卷筒侧折线段端板根部，与采用壳单元进行有限元计算的结果有一定差异，在有条件时建议采用实体建模进行计算，这样计算结果更接近真实情况。由以上计算显示，对于双折线卷筒的端板若采用传统计算方法设计，虽然满足了许用应力要求，但卷筒在实际使用时仍可能在工作过程中出现卷筒侧端板根部失效或开裂现象。

若假设端板所受轴向压力按钢丝绳层整圆周均布线载荷，利用I-IDEAS有限元计算后最大应力仍出现在卷筒侧端板根部，最大应力计算值σmax=161 MPa，端板最外缘最大变形量为δmax=0.46 mm。由此可见，在该假设条件下即使计算应力满足许用应力要求，在实际工作过程中卷筒侧端板根部仍可能出现失效现象。

本次计算选取的折线段对应中心角45°、直线段对应中心角135°，一般为了优化双折线卷筒设计，减少缠绕过程中的震动及延长钢丝绳使用寿命，折线部分应有合理的占比，一般为20%左右。据研究[7]折线部分的占比，主要由同层相邻钢丝绳间的间隙、钢丝绳间的滑动摩擦系数、卷筒直径以及缠绕的钢丝绳直径4个方面决定。摩擦系数越大则相应折线部分占比越小，节距越大折线部分占比越大。同时，钢丝绳半径与卷筒半径的比值r/R越大，折线部分占比越大。但是，若折线部分占比过大，钢丝绳在折线部分缠绕移动部分则过多，使该段钢丝绳可能产生不稳定及不规则排列，导致钢丝绳磨损加剧，减少钢丝绳寿命；如果折线部分占比过少，则钢丝绳在折线部分缠绕移动时，会突然产生较大冲击，减少钢丝绳寿命。

在公式推导过程中假设钢丝绳截面是圆形，在实际应用中钢丝绳应满足在最大载荷下也能保持其圆形截面形状。一般选用同向捻、钢芯、压实股、外层丝较粗且经过锻打的钢丝绳，直径一般为正公差，为公称直径的+2%～+4%。钢丝绳公差较大将使缠绕钢丝绳的折线交叉区域与卷筒轴向产生挫动，这种钢丝绳层间不稳定支撑将导致钢丝绳的损坏。

双折线卷筒是多层缠绕，所受应力非常复杂。在实际使用过程中，卷筒以及卷筒侧端板根部会有开裂、塌陷、开焊等现象。同时，在长期使用过程中产生的疲劳容易引起卷筒失效。本文上述计算仅是静强度条件下的计算，由于双折线卷筒在正常工作时，每完成一次工作循环，端板所受应力就会产生若干次变化，特别是在工作级别较高、利用率较大的场合，要求双折线卷筒能在相当长时间内正常工作，这样端板受力循环次数将非常大。因此，在设计双折线卷筒及卷筒端板结构时，除了要考虑满足静强度要求以及由此引起的变形，同时有必要进行疲劳强度计算。

4 结语

在设计双折线卷筒时，往往将考虑的重点集中在筒体本身，对于筒体两端连结的端板重视不足，造成卷筒失效或在多层缠绕时不能得到理想的缠绕效果。对于卷筒端板的受力，传统设计计算并非基于双折线卷筒的实际受力进行计算，而是假设总挤压力在侧板上均布、并引用薄板理论中受对称均布载荷的圆板公式进行计算。双折线卷筒若要达到理想的排绳要求，则卷筒两端法兰板在任何时间下都必须与卷筒保持垂直，即对端板的变形也必须要控制在一定范围内。这就要求端板除满足强度要求外，还必须要有足够的刚度。本文根据实际工况进行详细计算，并用有限元法对卷筒端板受力进行计算分析，其结果比传统方法更准确、可靠，同时可根据有限元计算得出的局部区域应力分布，为设计优化提供依据。因此，为了设计出理想的双折线卷筒，要综合考虑卷筒的结构形式，选择合适的钢丝绳并保持良好的润滑条件，详细计算卷筒各层钢丝绳的张力，精确计算端板受力，并利用有限元计算端板的应力和应变非常有必要。同时对于工作级别高的双折线卷筒有必要进行疲劳强度核算，以保证双折线卷筒能长期稳定的正常工作。