关注问题设计，引导素养提升

陈超

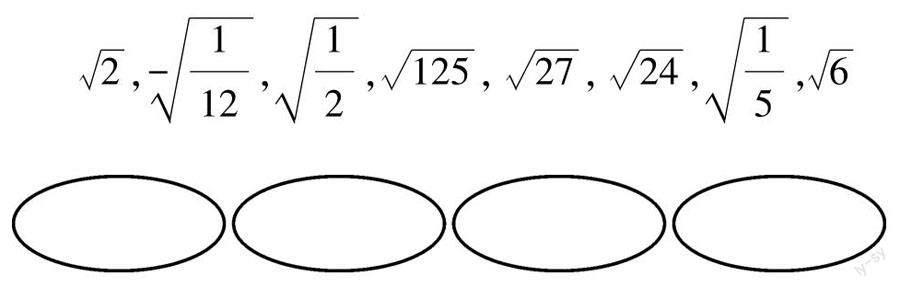
摘 要：《义务教育数学课程标准（2022年版）》指出，对于数与式的教学，教师应把握数与式的整体性.在二次根式的加减（1）的教学中笔者以关注数式通性、关注整体教学、关注素养培养为抓手进行教学设计.本文通过导入新知、建构新知、巩固新知、深化新知、回味新知、延伸新知六个环节开展教学，从而有序培养学生的核心素养.

关键词：课程标准；数式通性；单元视角；二次根式；核心素养

《义务教育课程标准（2022年版）》指出，对于数与式的教学，教师应把握数与式的整体性^［1］.因此，对于二次根式的加减运算，在教学中笔者主要以关注数式通性、关注整体教学、关注素养培养为抓手进行教学设计.所谓关注数式通性，就是引导学生在回顾前面学习的同类项的概念、合并同类项法则及整式加减的步骤的基础上，构建同类二次根式的概念、二次根式加减的法则以及二次根式加减的步骤；所谓关注整体教学，就是在整个单元视角下设计教学任务，同时让学生及时有效地类比前面学过的有理数、实数、整式、分式的相关知识点，并完成对应的生长性的思维导图；而素养培养，则是在具体的教学活动中，凸显“四基”和“四能”，关注综合实践，从而有序培养学生的核心素养.2023年10月，笔者有幸参加了苏州高新区教研室组织的教研活动，开设公开课一节，课题为“二次根式的加减（1）”，现将在磨课过程中的一些思考和教学过程以及反思整理如下：

1 教学分析

1.1 教材分析

“二次根式的加减”是苏科版八年级下册第12章第3节的内容，本节课是在学生已经学习了二次根式的定义、性质、化简和乘除法运算等相关知识和有了相关研究经验的基础上展开的.同时，二次根式的加减与之前学过的实数的加减、整式的加减、分式的加减又有着密切的联系，通过类比展开对二次根式的加减相关知识的研究能加深学生对数和式加减运算的研究方法的认识，也能为学生以后继续研究数和式加减运算奠定基础并且提供范式.在知识形成过程中，蕴含了类比、从特殊到一般、从具体到抽象等数学思想方法，对发展学生的运算能力、数据观念、应用意识等核心素养有积极的作用.

1.2 学情分析

（1） 从学生知识基础来看：学生已经学习了二次根式的定义、性质、化简和乘除法运算等相关知识，这套学习数与式的范式对学生学习二次根式的加减有良好的引导作用.

（2） 从学生数学活动经验来看：在之前“实数的加减”“整式的加减”和“分式的加减”的学习中，学生已初步了解了研究的路径，具备了一定的独立思考和归纳总结等能力.

1.3 视角分析

在大单元教学的视角背景下，引导学生归纳所学数与式知识点的结构框架、类比总结出研究数与式的一般路径：定义→性质→运算→应用，显得很有必要.为此，我打算在学生合作讨论的基础上，引导学生归纳所学数与式知识点的思维导图，从而体现数学知识点在课堂上的有效生成，真正做到以学生为主体，充分发挥学生的主观能动性，从而实现新课标要求的“整体把握教学内容，注重教学内容的结构化”，真正落实核心素养的提升.

2 教学设计

2.1 创设情境，导入新知

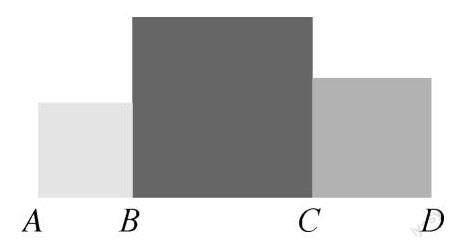
同学们，在刚刚结束的第19届杭州亚运会上，我国体育健儿不畏困难，不惧挑战，取得了201枚金牌、111枚银牌、71枚铜牌，共383枚奖牌的好成绩.小明同学想在亚运会手抄報上规划出三个区域画亚运会的吉祥物，如图所示.如果这三块区域设置成正方形.

（1）若从左往右的3个正方形的面积分别是4、16、9，求线段AD的长度.

（2） 若从左往右的3个正方形的面积分别是4a²、16a²、9a²（a＞0），求线段AD的长度.

你能说说这是什么运算吗？你是如何运算的呢？

设计意图：通过介绍生活中的实际问题，激发学生的学习兴趣.引导学生回顾前面学习的实数的加减法运算和整式的加减法运算.

（3） 若从左往右的3个正方形的面积分别是2、18、8或3、27、12或5、45、20.

你能分别列出求线段AD长的算式吗？

追问1：你能说说这是什么运算吗？

追问2：你能说说上面算式中的3组二次根式各有什么共同特征吗？

追问3：你能给具有这些特征的二次根式取一个合适的名字吗？

追问4：为什么取这个名字呢？

追问5：你能给同类二次根式下个定义吗？

设计意图：通过设置一系列追问，在对实数的加减法和整式的加减法回顾的基础上，引入二次根式的加减法的学习.同时，利用问题串引导学生类比前面学习的“同类项”的概念，并自主归纳总结出“同类二次根式”的概念.

2.2 类比学习，建构新知

经过化简以后，被开方数相同的二次根式，叫做同类二次根式.

找一找：请找出同类二次根式，并整理在框图内.

设计意图：通过设计“找一找”的数学活动，让学生进一步理解和应用“同类二次根式”的定义.通过对被开方数为分数的二次根式的化简，巩固前面学习的最简二次根式，从而为学生本节课的进一步学习打下基础.

2.3 数学运用，巩固新知

设计意图：以计算题“意外情况的出现”为素材，进一步提升学生发现问题、提出问题、分析问题和解决问题的能力.同时，引导学生发现类比的负迁移现象.通过“平方法”和“作差法”的渗透，进一步提升学生的运算能力和推理能力等.

例2 两个圆的圆心相同，半径分别为Rcm、rcm，面积分别是18πcm²、8πcm².求圆环的宽度（两圆半径之差）.

变式：两个圆的圆心相同，半径分别为Rcm、rcm，面积分别是18cm²、8cm².求圆环的宽度（两圆半径之差）.

设计意图：考虑到部分学生在计算被开方数是分数的二次根式时，经常算错.通过设计题目的阶梯，来分层引导学生计算生活中常见圆环图形的宽度，为学生学习被开方数是分数或分式的二次根式的化简，提供较好的范例，让学生积累一定的经验，从而提升学生的运算能力和应用意识，进一步感受数学和生活的紧密联系.

2.4 联系实际，深化新知

算一算：现有一块长8dm、宽3dm的木板，采用如图的方式，在这块木板上能否截出3个面积分别是4.5dm²、8dm²、4.5dm²的正方形木板？

设计意图：通过将问题情境中的三个正方形问题改编为生活中的截纸板问题，让学生感受到数学来源于生活，又高于生活，最终服务于生活这一理念.通过让学生自主探究“能否截出”，锻炼学生发现问题、提出问题、分析问题、解决问题的能力，从而有序发展学生的运算能力、推理能力和应用意识等数学核心素养.

2.5 课堂小结，回味新知

设计意图：给学生充足的时间来回顾第12章二次根式的学习过程，再引导学生对研究的路径进行小结，并完成思维导图.以回顾为契机，培养学生的总结能力，充分发挥学生的主体作用.让学生感受到数与式等数学知识的生长过程，关联数式通性，从而实现算法的顺利迁移^[2].

2.6 分层作业，延伸新知

必做题： 书本163—164页练习第1、2题.

选做题：整理已学的数与式的相关知识点，尝试从知识内容、过程方法、运算法则等角度自主构建知识框架.

设计意图：作业分必做题和选做题，让不同层次的学生都得到相应的发展.通过学生课后的独立思考、自主归纳进一步发展自身的数学核心素养.

3 教学反思

3.1 注重设问，培养能力

发现问题是研究数学问题的核心环节，那么在数学课堂教学中，老师通过一系列严谨缜密的设问，引导学生探索数学知识，就显得尤为重要.好的设问可以激发学生的求知欲、让教学目标落地生根并有序推进.相反，脱离实际的随意提问，会让学生一头雾水，抓不住重点.本节课通过一系列的追问，引导学生类比归纳总结出同类二次根式的定义和二次根式加减的法则和步骤，体现了较好的教学效果.通过引导学生由数学学科内实数的加减到整式的加减再过渡到本节课二次根式的加减，让学生感受数学知识的生长过程，也为学生在本节课学习结束时，总结、设计所学知识点的思维导图做铺垫.

3.2 类比迁移，发展素养

3.3 拓展延伸，回归生活

为了呼应本节课开始研究的拼在一起的三个正方形的面积问题，设计出“算一算”环节，让学生解决生活中的应用题.在学生充分讨论的基础上，小组合作探讨能否截出的具体意义，即：拼在一起的三个正方形的最大宽度需要不大于3dm，拼在一起的三个正方形的总长度不大于8dm，从而解决实际问题.让学生感受到数学来源于生活，又高于生活，最终服务于生活.同时，进一步发展学生的运算能力、推理能力、应用意识等核心素养.

参考文献：

［1］ 中华人民共和国教育部.义务教育数学课程标准（2022年版）［M］.北京：北京师范大学出版社，2022.

［2］ 李树平.关联数式通性 提升数学素养：“二次根式的加减（1）”教学设计与教学实施反思［J］.中学数学月刊，2023（7）：47-50.

［3］ 姜梦洁，刘冰楠.情境化数学问题的设计研究：以“弧度制”教学设计为例［J］.高中数学教与学，2023（20）：54-57.

［4］ 秦哲.关注问题梯度，提升解题能力：以“一次函数面积问题”教学设计为例［J］.中学数学，2023（20）：21-22+27.

［5］ 孙鋆.素养导向下数学概念问题链教学再设计：以“平面”概念的教学设计为例［J］.中小学数学（高中版），2023（7）：74-76.

［6］ 吴康.混合型切比雪夫方程探索［J］.数学之友，2022，36（5）：64-65.

［7］ 鲁和平.构造抛物線巧解向量题［J］.数学之友，2022，36（5）：69.

基金项目：江苏省教育科学“十四五”规划2021年度课题：“双减”背景下初中数学作业优化设计的研究（课题编号：C-c/2021/02/78）.