对一道函数公切线题的解法与变式探究

吴文忠

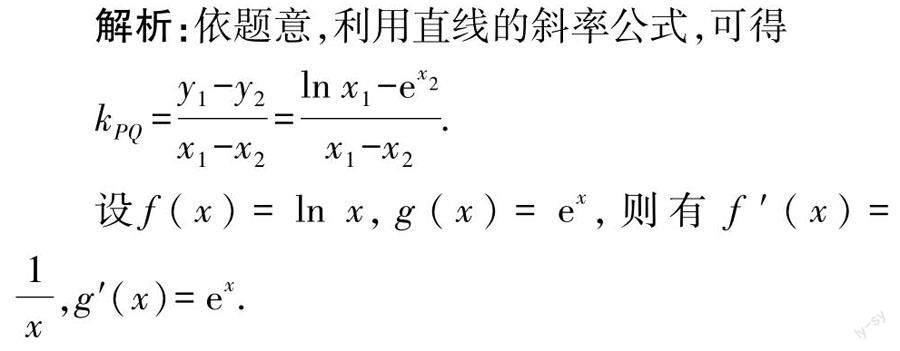
摘 要：多曲线（主要是两曲线）的公切线及其综合问题是近年高考中出现比较频繁的一类基本考题，内容涉及面广，知识融合度高.本文从一道指对数混合函数图象的公切线问题入手，探寻解决问题的技巧与方法，基于此进行多层次的合理变式探究，深挖问题的内涵与实质，引领并指导数学教学与复习备考.

关键词：函数；直线；公切线；导数

利用导数的几何意义来解决有关曲线的切线问题，一直是高考中比较常见的一类重点与热点问题，背景简单易懂，求解形式多样.特别是涉及两条及以上曲线（主要考查两条曲线）的公切线问题，新颖度高，创新性强，形式更加复杂多变，能更加有效地考查学生的“四基”以及数学应用能力等，凸现试题的选拔性与区分度，备受各方关注.

1 问题呈现

问题：若一条直线与函数y=lnx和y=e^x的图象分别相切于点P（x₁，y₁）和Q（x₂，y₂），則（1-e^y₁）（1+x₂）的值为                  .

本题研究的是涉及指数函数与对数函数的图象的公切线问题.随着一条曲线上切点的对应“动”态运动，带动另一条曲线上切点的变化，形成公切线的变化运动.但根据所求代数关系式，涉及切点的相关坐标的代数关系式是一个定值，为“静”态数值，“动”与“静”结合，创设一幅完美的画卷.

在具体求解过程中，抓住两条曲线所对应的公切线问题设切点，利用切线方程以及切线的斜率等基本要素来合理切入，通过公切线的统一性，化各自的切线为一条公共直线，从不同思维视角切入，利用不同的技巧方法来处理，从而求解目标代数表达式的值，实现问题的巧妙解决.

2 问题破解

方法1：（切线方程法）

解后反思：借助导数的几何意义，从每条曲线所对应的切线方程的求解入手，利用公切线的条件“合二为一”，构建相应的方程组，为问题的解决奠定基础，这也是解决此类两曲线的公切线及其综合问题最为常用的一种“通性通法”.利用切线方程来切入时，一定要注意参数之间的联系，同时注意代数式的恒等变形与转化，往往可以为问题的分析与求解创造更多的机会与空间.

方法2：（斜率公式法）

解后反思：借助公切线中两相应切点的设置以及直线的斜率公式，引入公切线的斜率，同时抓住导数的几何意义，构建对应切线的斜率，利用公切线在不同条件下对应的斜率是统一的，有效构建对应的关系式，为问题的进一步分析与求解打下基础，这是解决此类两曲线的公切线及其综合问题中的一种“巧技妙法”.多视角构建直线的斜率关系式，合理“聚焦”，产生共鸣.

方法3：（统一变量法）

解后反思：在解决此类两曲线的公切线及其综合问题时，两个切点中的多个坐标变量会给问题的分析与求解造成一定的困难，而统一变量法就显得非常重要，对于目标代数关系式的求解与应用等方面都有很好的帮助.合理选择其中某个变量（这里是公切线的斜率）加以统一处理，其他变量都以该变量来表示，这对于代数式的求值以及关系式的化简等方面都有裨益.

3 变式拓展

3.1 同阶变式

所以函数h（x）在（1，x₀）上单调递减，在（x₀，2）上单调递增.

又h（x₀）=x₀lnx₀-lnx₀-x₀-1=-lnx₀-x₀＜0，

当x→1⁺时，h（x）→-2＜0，则知函数h（x）的零点x₁在（x₀，+∞）上，

又h（4）=6ln2-5＜0，h（5）=4ln5-6＞0，则有x₁∈（4，5），可得n=4.

故填答案：4.

4 教学启示

4.1 归纳技巧方法

解决两曲线的公切线问题，核心是切点坐标，因为切点处的导数就是切线的斜率.公切线问题，应根据两个函数的图象在切点处的斜率相等，且切点既在切线上又在曲线上，列出有关切点横坐标的方程（组），通过解方程（组）或恒等变形等来分析与求解.

4.2 提升变式效应

在平时的解题过程中，要适时地将问题加以深入变形与拓展，借助“一题多变”，实现“一题多得”，久而久之，就能逐步培养学生灵活多变的数学思维，发散开拓的数学思想，创新应用的探索精神与创新意识，从而真正把对数学能力的培养落到实处，全面提高数学核心素养.