“三新”创设，夯实基础，素养应用

季峰

摘 要：在“三新”背景下，教学与学习更加重视改革与创新，强化数学基础知识与关键能力.本文就《统计》单元知识模块，通过复习教学的设计与安排，侧重于本质内涵，从构建知识网络，重视抽样方法，掌握统计图表与数据，拓展数学思维等层面与视角展开与应用，总结统计部分教学与复习安排，引领并指导数学教学与复习总结.

关键词：统计；图表；数据；复习；设计

在新教材（人民教育出版社2019年国家教材委员会专家委员会审核通过）、新课程（《普通高中数学课程标准（2017年版，2020年修订》）、新高考的“三新”背景下，《统计》单元的复习教学设计更加侧重于“四基”层面，合理创设知识网络与体系，注意获取统计数据的抽样方法的科学性，展示统计图表的直观性，凸显统计数据的应用性，拓展数学思维的灵活性等，有效进行单元复习教学设计与安排.

1 构造知识网络，理清结构系统

涉及《统计》单元章节知识模块，关键在于构建并形成对应的知识网络，联系起该章节中各个相关知识点之间的关联，全面理清单元结构系统，深化知识的理解与掌握，为综合应用等创设场景与条件.

《统计》单元章节知识网络的构建，可以从“四基”（数学基础知识、基本技能、基本思想、基本活动经验）视角来展开并合理构建，为章节知识的深入理解与掌握复习，搭建起一个充分知识节点的网络架构，为进一步发现问题、提出问题、分析问题以及解决问题等关键能力的提升，以及数学核心素养的发展与培养，奠定基础.

2 选择抽样方法，正确获取数据

《统计》单元中，涉及抽样方法的选择，主要遵循以下基本原则：（1）当总体的量较小，样本量也较小时，制签简单，号签容易搅拌均匀，可以采用抽签法；（2）当总体的量较大，样本量小，可以采用简单的随机数法；（3）当总体由明显差异的几部分构成时，往往采用分层随机抽样加以应用.

点评：在利用分层随机抽样进行概念判断与运算求值等问题时，要正确理解并掌握分层随机抽样适用的前提条件是总体可以分层、层与层之间有明显区别，而层内个体间差异较小，并结合比例分配进行运算求值.

3 掌握统计图表，正确识图用图

《统计》单元中，涉及的统计图表主要有频率分布表、频率分布直方图、折线图、饼图等基本图表形式，并结合相应的统计图表信息来合理分析并进行总体估计，为统计及其应用提供条件.特别地，频率分布直方图是统计图表中应用最为广泛且重要的一个基本图表，正确识别对应图中各元素的含义及对应意义，进而加以正确分析与应用.

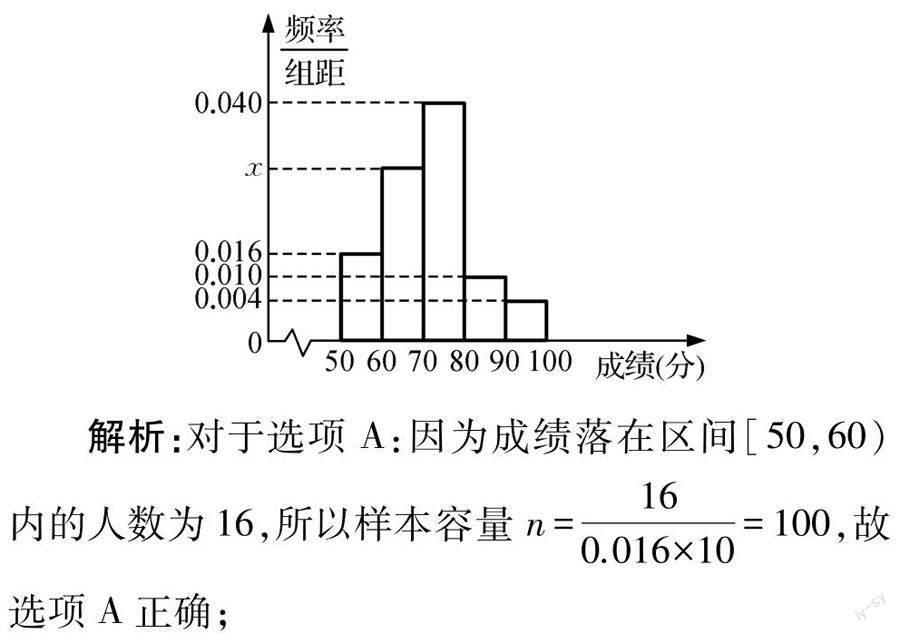
【例2】（2023届江苏省南京田家炳高级中学高三（下）期初数学试卷）（多选题）在某市高三年级举行的一次模拟考试中，某学科共有20000人参加考试.为了了解本次考试学生成绩情况，从中抽取了部分学生的成绩（成绩均为正整数，满分为100分）作为样本进行统计，样本容量为n.按照［50，60），［60，70），［70，80），［80，90），［90，100］的分组作出频率分布直方图，如图所示，其中，成绩落在区间［50，60）内的人数为16.下列结论正确的是（  ）.

A. 样本容量n=100

B. 图中x=0.030

C. 估计该市全体学生成绩的平均分为70.6分

D. 该市要对成绩由高到低前20%的学生授予“优秀学生”称号，则成绩为78分的学生肯定能得到此称号

对于选项B：因为（0.016+x+0.040+0.010+0.004）×10=1，解得x=0.030，故选项B正确;

对于选项C：学生成绩平均分为0.016×10×55+0.030×10×65+0.040×10×75+0.010×10×85+0.004×10×95=70.6，故选项C正确；

对于选项D：因为10×（0.004+0.010）+（80-78 ）×0.040=0.22＞0.2，即按照成绩由高到低前20%的学生中不含78分的学生，所以成绩为78分的学生不能得到此称号，故选项D不正确；

故选择答案：ABC.

点评：通过频率分布直方图这一统计图表的正确分析，合理识图并用图，通过计算相应的统计中的频率与频数，样本容量与总体容量，平均数等相关数据信息的计算来分析与判断，解决频率分布直方图的实际应用问题.

4 刻画统计数据，实现总体估计

《统计》单元中，涉及的重要的统计参数主要包括平均数、中位数、众数与方差、标准差等，借助不同的统计参数，反映样本数据的集中趋势或数据波动大小等.结合具体应用并借助统计参数的几何意义，加以合理选用与比较，进行合理的决策与应用判断.

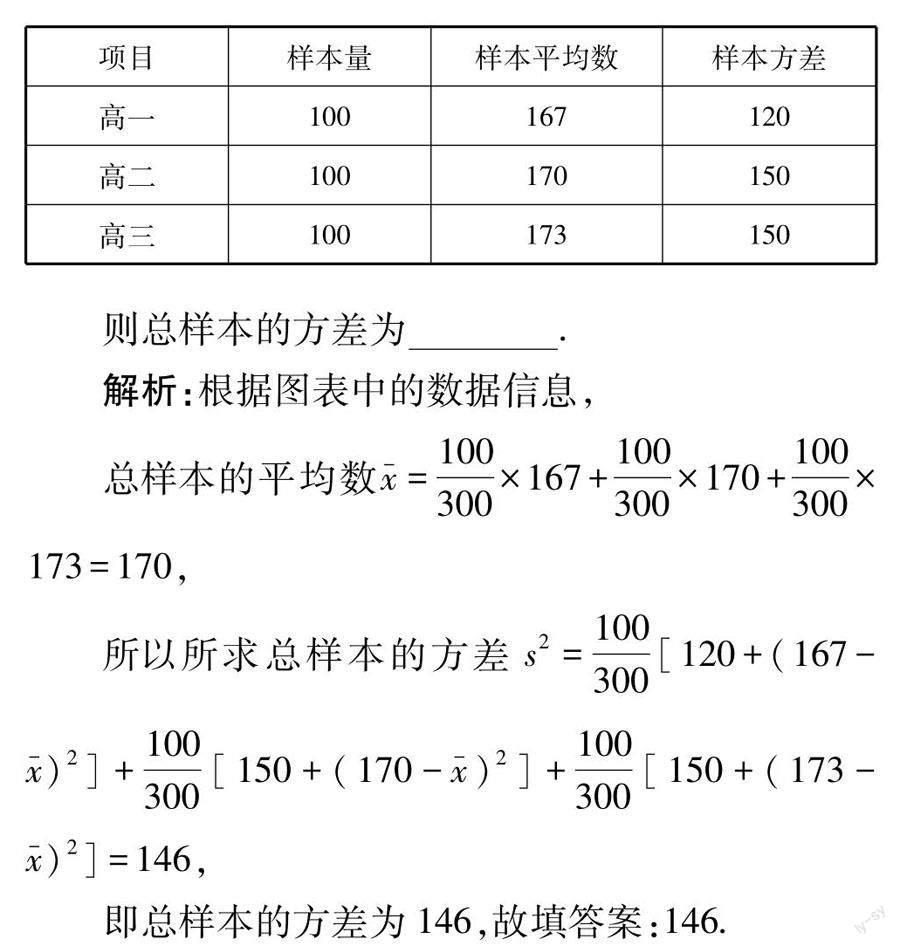
【例3】（2023届湖北省武汉市武昌区高三年级质量检测数学试卷）某校采用分层随机抽样的方法采集了高一、高二、高三年级学生的身高状况，部分调查数据如下：

点评：在处理统计中涉及样本平均数与方差的综合应用问题中，关键就是正确确定分层随机抽样的层数，以及对应的概念，结合相关的计算公式与性质加以熟练掌握，并结合实际应用问题的场景与现实实际来综合处理与决策.

5 重视数学思维，关注数形结合

《统计》单元中涉及众多的数学思维，主要有函数与方程思想，数形结合思想等.特别的，数形结合思想是通过数与形之间的对应关系和相互转化来解决问题.而在统计中，常结合统计图表进行数形结合，实现对数据的分析，进而来解决问题.

【例4】某公司开发了一款手机应用软件，为了解用户对这款软件的满意度，推出该软件3个月后，从使用该软件的用户中随机抽查了1000名，将所得的满意度的分数分成7组：［30，40），［40，50），…，［90，100］，整理得到如下频率分布直方图.这1000名用户满意度的第25百分位数是                 .

解析：根据频率分布直方图，可知（0.005+0.010）×10=0.15＜0.25，（0.005+0.010+0.025）×10=0.4＞0.25，

所以第25百分位数落在区间［50，60），

设1000名用户满意度的第25百分位数是x，则0.15+（x-50）×0.025=0.25，解得x=54，

即1000名户满意度的第25百分位数是54，故填答案：54.

点评：熟练识别频率分布直方图，正确理解第25百分位数，借助数形结合的直观分析，以及统计数据的数学运算来综合与应用，是解决此类问题中的关键所在.

6 总结

在“三新”（新教材、新课程、新高考）背景下，进一步落实“双减”政策与新改革理念，积极贯彻《总体方案》要求，《统计》单元復习教学设计与安排在寻求基础、本质、能力、创新等的基础上，更多侧重数学基础与关键能力的考查，坚持开放创新与核心素养导向，更加注重数学创新意识与创新应用.

参考文献：

［1］ 马茂年，吕增锋.新课标下的高中数学“统计”教学要凸显“四个特性”［J］.中学教研（数学），2021，489（11）：1-4.

［2］ 张世静，栾庆芳.初、高中数学“统计与概率”教学衔接的研究［J］.理科考试研究，2022，29（21）：11-15.