信息技术辅助下的“以测为基，精准教学”

谢纯蓥 万林峰

【摘   要】信息技术辅助下的常态化“测试”能及时帮助教师了解学情，精准实施教学。以人教版教材二年级上册《数学广角——搭配（一）》一课的教学为例，教师通过信息技术辅助下的常态化“测试”，可呈现“为教学设计奠定基础”“为课堂调控提供基础”“为后继学习打牢基础”的课堂教学样态。

【关键词】精准教学；学情前测；信息技术

精准教学的核心在于“精准”，而做到“精准”的关键是对学情充分了解。“测试”能帮助教师更好地了解学情。完全依赖纸笔的测试方式，使教师在阅卷、数据整理与分析中都投入较多精力，不利于有效“测试”的常态化。因此，可采用信息技术辅助教师展开“测试”，促进日常教学的日益精准。下面，以人教版教材二年级上册《数学广角——搭配（一）》为例，具体说明如何利用信息技术辅助前测、课堂教学和巩固练习测，实现精准教学。

一、信息技术辅助“前测”，为教学设计奠定基础

二年级的学生在生活中已经有丰富的“搭配”经验，通过本课的学习，学生需进一步理解并掌握“搭配”的方法，有序地进行搭配。学生在课前对“搭配”究竟了解多少？能否有序地進行“搭配”？怎样才能做到“不重复、不遗漏”？为了精准地找到每个学生的学习起点，教师选取了要进行教学的二（10）班的41个学生，对他们进行了前测。

前测题1：用1、2和3组成两位数，每个两位数的十位数和个位数不能一样，能组成几个两位数？请把所有组合情况都写出来。

前测题2：小明、小红、小东3个小朋友在拍照，选其中2个坐一排合影，有多少种不同的“坐法”？请把所有“坐法”都表示出来。

前测采用线上的形式进行。学生在学校利用“作业整理”时间独自完成前测，并在线上提交。教师则利用前期设计的“小程序”，让计算机自动“批阅”学生的前测作业，并根据学生的答题情况整理数据。测试结果如表1所示。

结合数据可以发现，第1题约51%的学生能够完整写出6个两位数，只有少数学生能有序地写出所有两位数。约39%的学生会写一些两位数，但出现了重复或者漏写的情况，其中约10%的学生不理解题意。有出现十位数和个位数重复的，如11、22、33；有出现三位数的，如123。第2道前测题，约有44%的学生做对，但只有少数的学生能够运用数字、字母、图画等形式将3个小朋友符号化，采用定位法、交换位置法有序地搭配出6种不同的坐法。其中约29%的学生能够写出6种不同的坐法，但是没有进行有序的搭配。约44%的学生在搭配的过程中有重复或者遗漏。还有个别学生不理解题意导致乱写，如三个三个排列的。通过对前测的分析，学生虽然对“搭配”已具备一定的经验，但并不太了解它背后的道理，且学生存在个体差异，大部分学生在“搭配”时难以有序思考。因此，本节课的教学重点为“理解有序思考的重要性及至少掌握一种有序思考的方法”。教师可以尝试先借助平板电脑进行现场操作，在丰富学生直观感受的同时，收集整理学生作品的相关信息，从而聚焦学生个体差异，精准把脉学情，了解学生的认知起点。再结合“提问”和“交流”这样的经典教学方式，引导学生深入思考，让他们在操作、比较、辨析等数学活动中体验数学思考的有序性。

二、信息技术辅助“教学”，为课堂调控提供基础

信息技术辅助下的“测试”，不仅可以在课前使用以了解学情，也可以在教学导入、活动展开等环节使用，作为教师进行课堂调控的基石。

（一）教学导入

在信息技术的支持下，教师可以快速了解学生的整体答题情况，并能精准地找到问题解答“又快又准”的学生，以及解答过程中出现错误的学生，与他们进行课堂对话，引导他们对有序思考的方法有基本认识。

教师先让学生介绍生活中的搭配现象。

师：生活中，至少要有两种不同的事物才能完成“搭配”。那么，在数学中有没有搭配问题呢？

生：有的。数字和数字可以搭配。

师：这里有两个数字（课件出示数字1、2），要求搭配出没有重复数字的两位数，你能进行搭配吗？

学生运用平板电脑在平台上进行搭配，完成情况如表2。

教师在课件中展示学生的三种答案。

第一种：12、21。

第二种：12、21、11、22。

第三种：12、21、12。

师：哪一种是正确的？

生：第一种。

师：后面两种错在哪里？

生：第二种里面的11、22，不是数字“1”和数字“2”搭配，而是“1”和“1”搭配，“2”和“2”搭配。

生：第三种里的“12”出现了两次，重复了。

师：不错。数字“1”和数字“2”只能搭配出12和21。请你想一想，为什么数字“1”和数字“2”搭配出的两位数是两个，而不是一个或三个？

生：因为数字“1”和数字“2”可以左右交换位置，所以有两个。

生：因为数字“1”只能和数字“2”搭配，不能和自己搭配，“2”也是，所以只有两个。

师小结：同学们说得都很有道理，“1”和“2”两个数字搭配的时候可以互相交换位置，所以至少有两个。又要求没有重复数字，即不能自己和自己搭配，所以也只能有两个。

（二）教学活动过程

教学活动要想真正基于学生的现实基础，可以从“前测”中学生的答题情况开始展开。“前测”题目与数据的再利用，能更加有效地促进学生对自我认知的反思与重构。

1.交流三种不同的写法

师：这是我们在课前做的第一道题目（课件出示前测题1），有7个同学不重复、不遗漏地写出了所有答案。

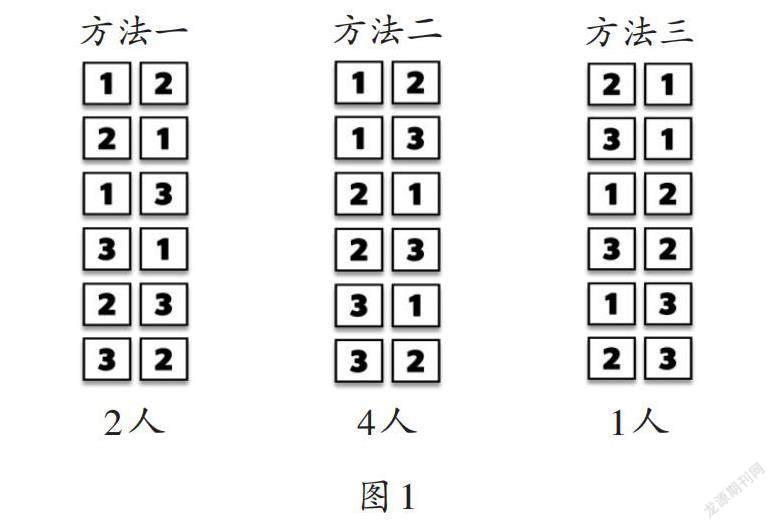
师：（课件出示图1）请同学们仔细观察第一种方法，想一想，这些同学是用什么方法写出答案的？

生：第一种方法是先写“12”，然后交换一下左右位置，变成“21”；再写“13”，同样交换一下左右的位置，写出“31”；最后写“23”，交换一下位置，写出“32”。

师：先写出一个两位数，然后通过交换个位和十位数字的位置再写出一个两位数，这种方法一般称作“交换位置法”。（板书：交换位置法）

师：有4个同学是用第二种方法做的，仔细观察，想一想，他们又是怎么写完整的？

生：这种方法是先在十位写“1”，然后在个位上写“2”或“3”，所以可以写出12和13；再在十位上写“2”，个位上写“1”或“3”，可以写出21和23；最后在十位上写“3”，个位上写“1”或“2”，可以写出31和32。

师：简单地说，先确定十位上的数，再来写个位上的数，这样也能不重复、不遗漏地写出来。这种方法叫“固定十位法”。（板书：固定十位法）

师：有1个同学选择了方法三，这种方法是什么意思呢？

生：他和第二种方法刚好反了一下，是先确定个位上的数，再来写十位上的数。

师：除了可以先固定十位，还可以先固定个位。这种方法叫“固定个位法”。（板书：固定个位法）

2.交流错写的情况

师：（课件出示图2）发现有同学是这样写的，大家仔细看看，说说你有什么看法。

生：他们有的重复了，有的漏掉了。

师：为什么会重复写或漏写呢？

生：因为他们太粗心。

生：因为他们没按前面同学的方法写。

师：是的。搭配时不仅要仔细，还要使用合适的方法，才能做到有序思考，从而保证不重复、不遗漏。

教师出示题目：在数字1、2、3、4、5、6、7、8、9中，任选3个数字，组成两位数，每个两位数的十位数和个位数不能一样，能组成几个两位数？

师：请你选择3个自己喜欢的数字，用刚学过的方法写一写。（师生校对答案后，白板出示统计情况，如表3）

师：我们尝试过用这三种不同的方法来进行搭配。那么这三种方法，你更喜欢哪一种？

生：我喜欢固定十位法，因为我发现用这种方法写出来的数是有顺序的。

生：我喜欢用交换位置法。

师：不管是用“固定十位法”还是“交换位置法”，都能保证我们做到不重复、不遗漏。

3.讨论一个数字是0的情况

师：在刚才那道题中，我们发现任意3个数字都可以组成6个不同的两位数。大家有没有想过，为什么像这样的3个不同数字都可以组成6个不同的两位数呢？是不是无论哪3个数字都能组成6个两位数呢？

生：（齐说）能！

教师出示题目：如何用“0、2、3”这3个数字组成6个不同的两位数？

师：请大家想一想，写一写。

（学生独立做题，教师巡视）

师：怎么都只写出4个？

生：这里有个“0”。

生：因为“0”是比较特殊的数字，它不能写在十位上。

生：不是随便3个数字，都能摆成6个不同两位数。

三、信息技术辅助“巩固练习测”，为后继学习打牢基礎

信息技术辅助下的“测试”在巩固练习阶段同样适用。“巩固练习测”可以了解学生对知识的掌握情况，还可以让学生在练习中及时调整，促进知识的迁移，为后继学习打牢基础。

在信息技术辅助下即时开展“测试”，能“精准”地诊断出学生真实的知识经验，使学情起点可视化。教师能依据“测试”来把握学情和教学起点，确立精准的教学目标，设计出有针对性的教学方案，同时提高学生学习过程中的反馈效率。

（1.浙江省绍兴市上虞区百官重华小学 2.浙江省绍兴市上虞区教师发展中心）