以IYPT赛题圆柱体骰子为例探讨非质点物体碰撞问题

郭逸兮 杨 艺 尹 硕 范 婷

(石河子大学理学院，新疆 石河子 832000)

物理教学过程中，对于碰撞问题，大部分教科书都会涉及.人教版高中物理课本[1]中讲述了可看作质点的物体的碰撞.在大学物理力学教程中，[2]总结了惠更斯和牛顿在这方面的研究，并介绍了恢复系数概念.并在例题中展示了圆柱体在完全非弹性情况下的碰撞.在奥林匹克竞赛物理教程中，[3]对以轻杆连接的小球的碰撞进行了讨论.而李海龙先生和郑金先生也曾对竞赛中的该类问题处理做了有借鉴意义的讨论.[4-5]在以上方法处理的问题中，题干里面常有与光滑的面进行碰撞，或者是碰撞期间的摩擦力忽略不计等设定.而在一些比较贴近现实的问题中，摩擦力是否可以忽略不计呢？

尹小刚先生曾经对这个问题进行了研究.[6]该篇论文中，假设小球在平行于碰撞面的方向有水平分量，并给出结论，摩擦力在碰撞过程中产生的冲量是不可忽略的.而对于碰撞时有水平分量，且有转动的情况，刘延柱先生曾经做过相关的研究，[7]即摩擦碰撞的Kane难题.文中特别指出，如果用恢复系数去处理该类问题，就可能造成能量不守恒的情况.

笔者以IYPT赛题圆柱体骰子为例，建立了包含摩擦力的碰撞理论，避免了采用碰撞系数，并以程序计算和验证二次碰撞的实验进行验证.

1 质点碰撞理论的局限

1.1 反弹系数应用误区

首先可以这样考虑，假如有一个很理想的长方体与水平地面成某一夹角，自由落体，落在地面上.这种情况下的碰撞，该如何考虑？显然以不同角度落在地上的圆柱体，弹起的高度是不一样的，如图1，也就是说在这个问题里面并没有一个常数可以用来表示反弹高度与下落高度之间的关系.因此碰撞系数这一概念在该类问题中不再适用.

图1 各角度落下反弹高度不同

因为在碰撞过程中碰撞使圆柱体产生了旋转，而只要存在这个旋转，转的速度不同，所弹起的高度也不同，如果坚持用圆柱体材料本身的弹性系数来进行计算的话，会发现，碰撞之后的能量大于初始能量.例如某圆柱体弹性系数e=1，以角度θ从高度h下落，与地面碰撞，由于e=1，其碰撞前后速度相等，那么显然可以回到初始高度，但这是由于碰撞圆柱体产生了旋转，所以产生了额外的转动能量，此时圆柱体具有的能量大于初始能量，故以碰撞系数解决此问题的思路不适用.前人在处理旋转的球体碰撞问题中遇到过能量增加的情况，即Kane难题，[7]二者都是在产生转动的碰撞中错误使用碰撞系数造成的.

1.2 水平速度的产生

如果不使用弹性系数而直接使用高中竞赛中常用的以冲量为出发点的碰撞理论来处理圆柱体的碰撞问题，会发生什么情况呢？

此处简单交代清楚以下公式及物理量：

角速度与冲量关系如下，其中J为转动惯量，l为接触点到质心的距离

(1)

竖直速度与冲量关系如下

(2)

由机械能守恒，可推得落地前的速度

(3)

不考虑摩擦，整体能量守恒

(4)

将(1)-(3)式代入(4)式得

(5)

解得

联立了能量方程、动量方程和角动量方程，发现确实可描述该问题.但由于忽略了摩擦力，碰撞后质心位置不会变化，而实际上，圆柱体如果进行自由落体的话，是会产生水平速度的，碰撞前后情况如图2.

图2 碰撞前后图片截取

我们用Tracker软件进行了位置追踪，得到的图像如图3.

图3 Tracker逐帧追踪

提取其坐标点，进行拟合后如图4.

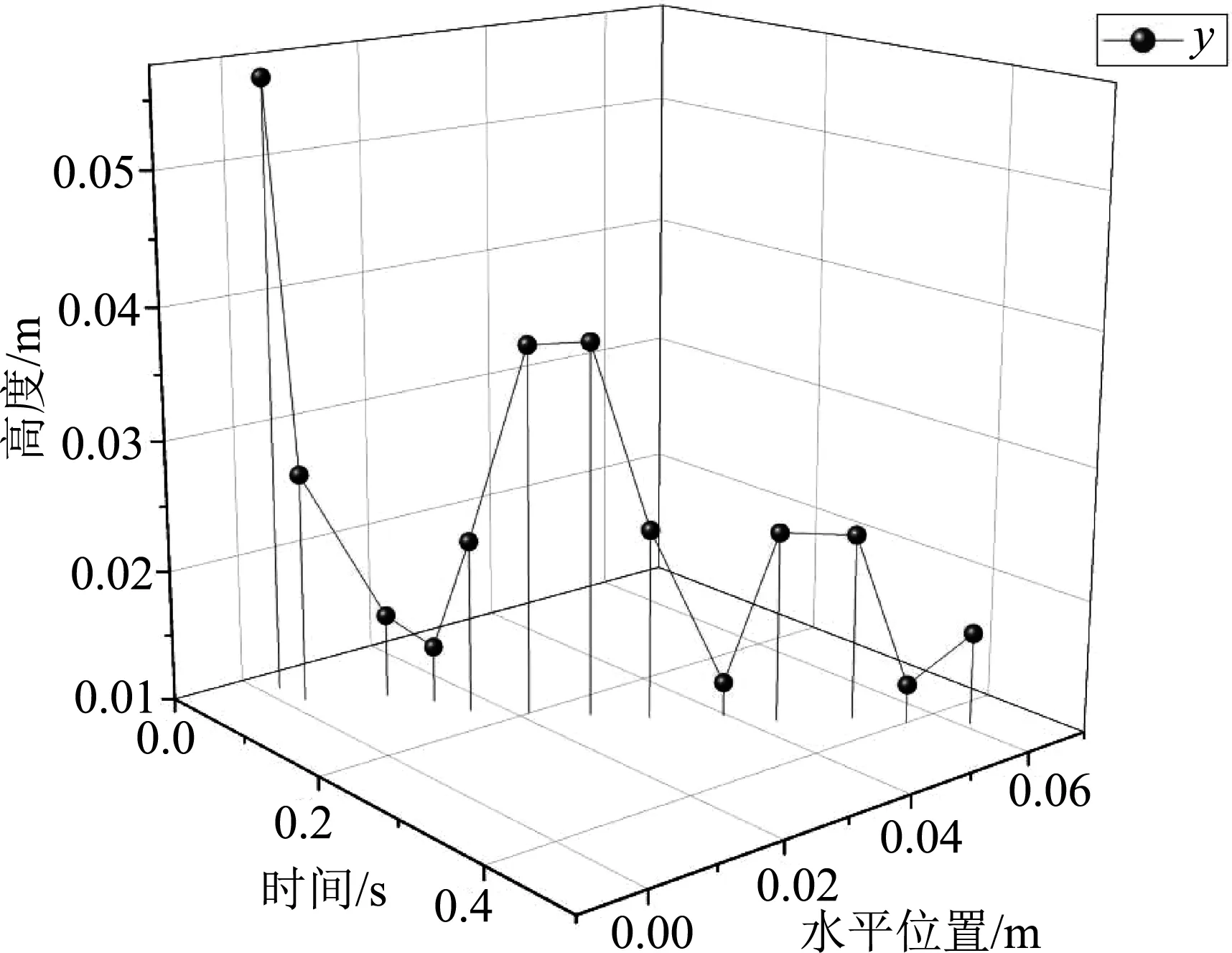
图4 对位置的轨迹拟合

忽略摩擦力的碰撞理论无法解释此时产生水平速度的原因，与实际情况有较大偏差.

2 非质点碰撞理论的建立

2.1 建立必要性

历年IYPT赛题中和碰撞理论相关的问题，往往研究论文极少.例如2022年第7题圆柱体骰子中涉及的碰撞问题，如果采用常用的不考虑摩擦的碰撞理论，会发现这个圆柱体骰子无法停下，因为没有任何的能量损失，投掷结果便永远无法得知.所以建立一个讨论摩擦力作用下的碰撞理论十分必要.

2.2 模型简化

由于圆柱体本身的对称关系，可以看到，不管它以何种水平夹角落到地面上，运动区间都是其质心-受力点连线所在的竖直平面.故在这里可以采用二维化的方法处理问题.

由于不同材料恢复弹性形变的耗能是不同的，并且没有一个统一的理论可以将其描述，这里只讨论恢复弹性形变的耗能可以忽略不计的材料.

由于现实中骰子本身的性质，只讨论碰撞形变极小，恢复时间极短的材料，且在这种情况下，不存在因摩擦力使运动反向的情况.

2.3 正方向和参数设定

为方便确定碰撞中的受力方向和判断最终状态，做如下规定.

速度分量和角速度正方向如图5所示.

图5 正方向的标注

接触点速度在水平上投影的方向表示为j，

若vx+ωlsinθ<0，则j=-1；

若vx+ωlsinθ>0，则j=1；

若vx+ωlsinθ=0，则j=dir.

由于第1次碰撞之前接触点水平速度为0，但是碰撞途中产生了速度，定义dir用于代表第1次碰撞时产生的速度的方向.

若cosθ>0，dir=-1；若cosθ<0，dir=1；若cosθ=0，dir=0.

相关参数及变量：

初始条件：夹角为θ0，初始高度为h，初始角速度w0=0，初始速度v0=0；

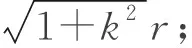
物理参数：物体重量为m，与地面摩擦因数为μ；

第i次碰撞前水平速度为vi-1x， 竖直速度为vi-1y，角速度为ωi-1；

第i次碰撞后水平速度为vix， 竖直速度为viy，角速度为ωi， 下落时间为ti.

2.4 碰撞过程中摩擦力做功

由冲量定义，可以把碰撞中所受的力写为冲量关于时间的一阶导

(6)

摩擦力为正压力与摩擦因数μ的乘积

f(t)=-jμF(t).

(7)

将(6)式代入(7)式得

(8)

受力点在该极短时间的位移可以写为平动与转动的组合(如图6)

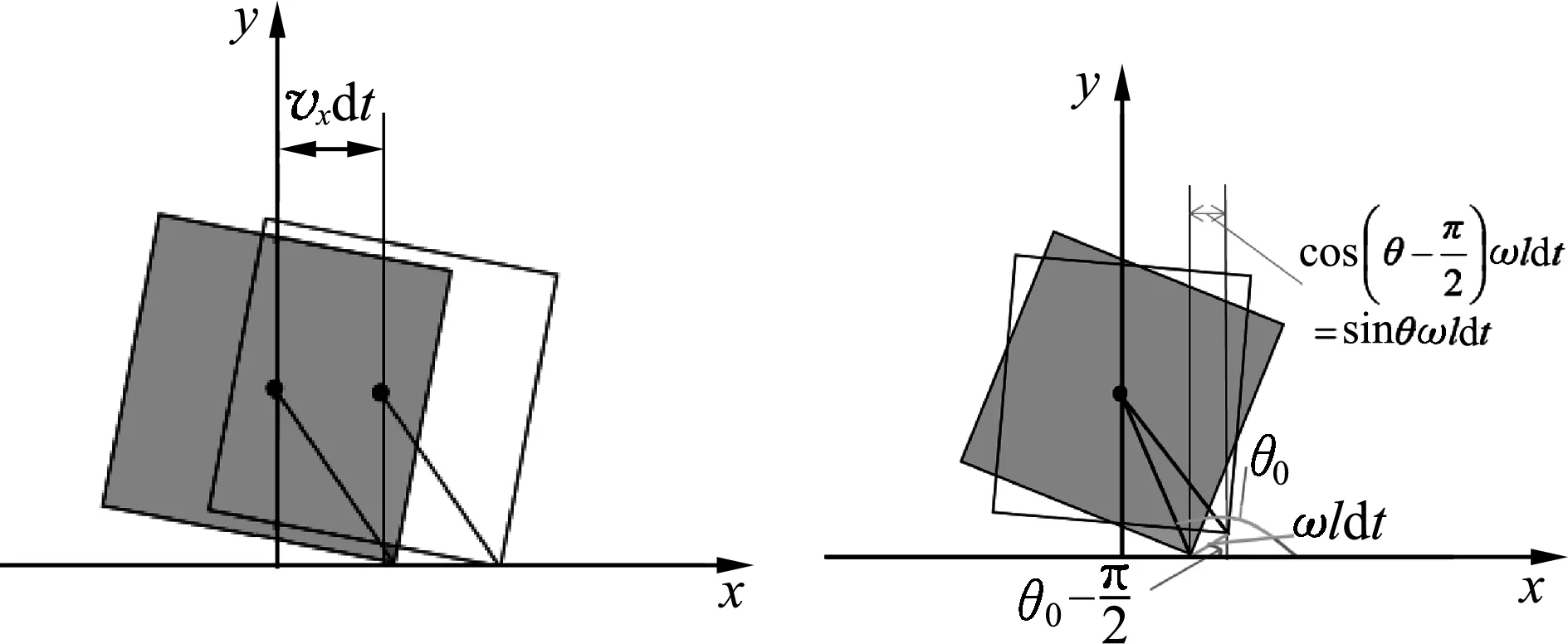
图6 极短时间内的位移关系

dx=v点dt.

(9)

dx=v(t)dt+ω(t)lsinθdt.

(10)

在碰撞过程中水平速度关于时间的函数为

(11)

其中I(t)是该次碰撞中对应时间冲量变化的总量.

在碰撞过程中角速度关于时间的函数为

(12)

在碰撞中某一瞬间摩擦力做的功为

dW=fdx.

(13)

代(8)(10)式入(13)式得

dW=fdx=

(14)

将(11)(12)式代入(14)式得

(15)

两边同时积分得

(16)

得到做功关于冲量的表达式为

(17)

2.5 反弹过程中各参数间的关系

在从初始高度下落的过程中，势能向动能转换(如图7)

(18)

由于这里认为碰撞系数为1，不会因碰撞形变损失能量，所以每一次碰撞前后的能量差为摩擦力做功，为

(19)

(20)

由角动量定理知动量的改变量等于冲力矩之和为

-Ilcosθi-1-jμIlsinθi-1=JΔωi-1.

(21)

ωi=ωi-1+Δωi.

(22)

由质心的冲量定理知

I=m(viy-vi-1y).

(23)

新水平速度为原水平速度和由摩擦力造成的改变量之和，为

(24)

易知所有涉及的物理量都可以写为关于冲量I的函数.

将(20)-(24)式代入(19)式中，由于其中每一项都含I2，I或者常数，可得

(25)

整理后可得aI2+bI+c=0，其中

jucosθi-1sinθi-1).

(26)

b=vi-1y-ωi-1lcosθi-1.

(27)

由于常数项互相抵消，所以常数项c=0.故

(28)

整理得

(29)

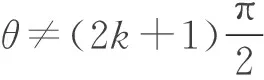
(30)

Ii=-2mvi-1y.

(31)

综合以上可以写出第i次和第i-1次碰撞结果的关系

(32)

(33)

(34)

2.6 验证

根据以上结论，利用Matlab编程，计算第1次碰撞后的机械能与初始机械能比值.将如下参数代入：r=1，μ=0.1，m=1，k=1，θ∈(45°，135°),h∈(10,60)，得到结果如图8所示.

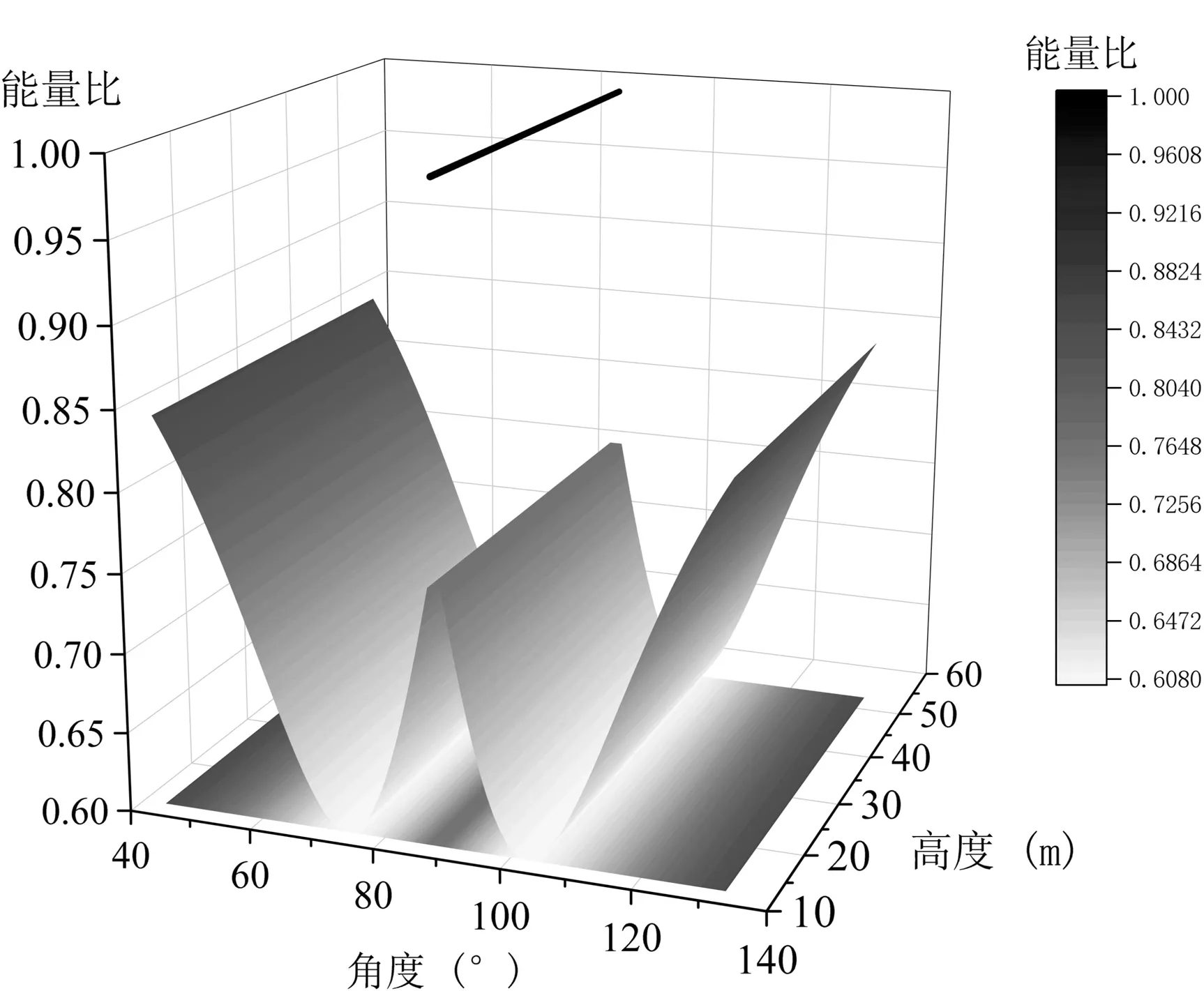
图8 碰撞前后的机械能之比

结果中未出现碰撞后能量超出初始状态的情况，均克服了类似Kane难题，即因碰撞造成能量增加的情况.其中在90°时，由于不发生转动，作用点水平移动完全为0，无能量损耗，与预期结果相符.

注意到理论计算中，在柱体以接近水平的角度落地时，会在极短的时间内发生第2次碰撞，采用慢速摄像观察发现，实际情况中也会2次碰撞，如图9，第1次碰撞后顺时针转动，紧接着发生第2次碰撞，导致放倒后观察现象为逆时针旋转.

图9 短时间内发生第2次碰撞

要注意的是，在之后的碰撞中，圆柱体产生了旋转和水平速度，并且由于旋转，再次落地的时候，落地角便不再是原先的角了，在这个时候就需要进行角度变换了，不能单纯地使用θi=θi-1+Δθi-1来计算，本文重点为碰撞过程，此处角度变换不做详细说明.

3 结论

本文从传统碰撞理论教学方法入手，总结了其中对于现实问题描述的不足.以2022年IYPT赛题圆柱体骰子为例，提出了一种更符合实际情况的碰撞理论，并针对理论计算中出现夹角较小时存在的短时间内的二次碰撞，做了实验验证.本文中的分析方法，有效地避免了含摩擦的碰撞理论常碰到的Kane难题，是对现有教学中碰撞理论的一种有力补充.但是，当碰撞的材料恢复形变有耗能时，此理论是不适用的.现阶段暂未完全探究清楚各类材料形变耗能的解析解，只有一些特殊材料的经验公式，[8]而这些经验公式只符合特定材料.本文理论目前只适用完全弹性碰撞材料，如何与原先含弹性系数的理论相兼容，需进一步探索.