立足认知起点 明晰算理算法——“口算乘法”的教学实践与思考

浙江省台州市椒江区中山小学杨司校区 王嘉嘉

“多位数乘一位数口算乘法”是人教版数学三年级上册第六单元第一课时的内容。学生在“表内乘法”和“100以内的加减法”的学习中，已经积累了一定的知识、经验和能力。这些已有的认知对学生的学习起着多大作用？教师又该采取怎样的教学方式落实教学目标？对此，笔者对本课做了如下教学分析、实践与思考。

一、双向探析，寻根追因知现状

（一）学生认知背景分析

学习“多位数乘一位数口算乘法”之前，学生就具备了一定的逻辑起点：正确口算100以内加减法、熟练掌握表内乘法计算。故不能将它们置于零起点教学。那么，我们该如何根据学生已有的经验整体把握设计教学？

基于以上思考，笔者对本校三年级169名学生做了前测，前测题为：请用你喜欢的方式计算13×2，并写出你的思考过程。前测结果见表1：

通过统计，学生借助画图、连加、分步、列竖式的方法可以得出正确结果，且正确率高达90.53%。但学生中能明晰多位数乘一位数算理的却很少。因此，笔者认为在教学中要关注学生的逻辑起点和现实起点，整体把握合理设计教学。

（二）教材编排分析

“多位数乘一位数口算乘法”主要建立在表内乘法的基础上进行教学，其后续教学内容还包括笔算乘法和用乘法解决问题两部分。教师在设计教学时怎样才能做到基于教材又高于教材呢？为此，笔者对人教2001年版和2022年版教材进行了比对。

以2001年版教材为例（见表2）。教材中例1以游乐园为背景展开教学，引导学生利用连加、几个几的知识推理学习整十、整百、整千数乘一位数。例2的教学围绕“带250元钱够吗”这一问题展开，在学生无法准确计算得数的情况下无形中“逼”着学生用估一估的方法解决29×8大约等于多少。

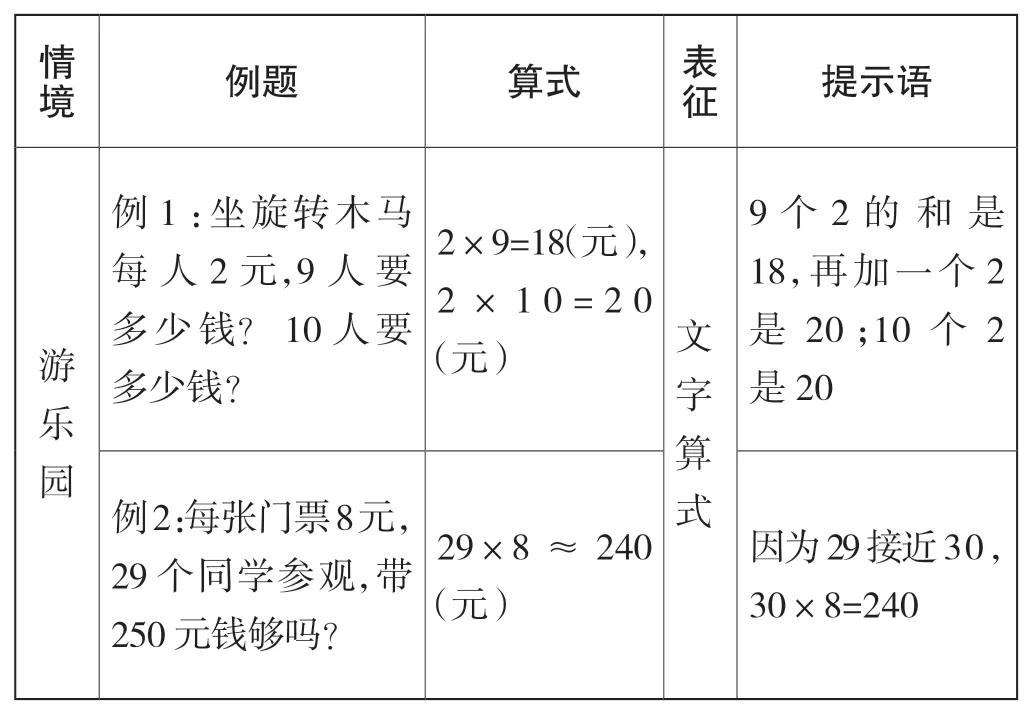
表2 人教2001年版教材相关情况

以2022年版教材为例（见表3）。教材继续沿用了之前的游乐园主题情境，以“3人要多少钱”为问题核心，在情境中引导学生利用小棒图，结合连加和计数单位帮助学生理解20×3、12×3，通过算理算法的迁移完成200×3和12×4的学习。

表3 人教2022年版教材相关情况

对比新旧教材，笔者认为2022年版教材的编排更为合理。究其原因有以下几点：一是2001年版教材从口算乘法一下跨越到用估算解决问题显得较为仓促，同时把估算作为唯一解题策略方法单一，不符合三年级学生的认知规律；二是笔算要用到整十、整百、整千数乘一位数和表内乘法，所以2022年版教材在一位数乘整十、整百、整千数的口算后紧跟两位数乘一位数（不进位）的口算，更显知识的连贯性；三是2022年版教材新增的两幅小棒图更具直观操作、数形结合的优点，能有效帮助学生理解算理、算法。

基于以上分析，可知口算是学好笔算的前提，为了更好实现本课的教学目标，笔者在教学中利用小棒图这一抓手，试图让学生通过数形结合、对比沟通等方式沟通多元表征背后的运算原理，在操作探究、迁移类推中总结算法，提升学生的运算能力。

二、四步实践，聚焦问题理脉络

（一）创设中唤起意义

情境创设是利用熟悉的参考物，帮助学生将要探究的概念与熟悉的经验建立联系，引导他们利用经验来解释说明，形成自己的科学知识。计算学习往往枯燥乏味，机械、公式化的学习更易使学生产生厌烦心理，进而导致对数学学习渐失兴趣。创设怎样的情境更入情呢？笔者特意选择了贴近学生实际生活的游乐园情境，试图以境引情，激起学生的学习兴趣。

【教学片段一】

教学出示：游乐园情境图。教师引导“瞧，秋天是游玩的季节，这是游乐园项目价格表，3个小朋友游玩”，让学生提出用乘法解决的数学问题并列式。

总之，房屋建筑工程在社会中日益增多，直接影响到整个社会的和谐稳定。因此，保证房屋建筑工程的施工质量具有十分重要的意义。然而，在施工管理中会出现各种各样的问题。此时，有必要采取相应的对策来保证施工质量。本文主要对此进行了详细的分析，为相关人士提供参考。

当学生呈现“5×3=15，8×3=24，12×3=36，15×3=45，20×3=60”这几种方法后，笔者提问为什么都能用乘法来计算，以此引出乘法的运算意义。

培养学生的运算能力，理解运算意义是前提，而让学生在具体情境中体验运算的意义可提高学习的实效性。故笔者选择2022年版教材沿用的、学生熟悉的“游乐园”主情境，并适当修改价格表为后续教学服务。在学生得出一位数、整十数、两位数乘一位数的算式后，以“刚才的问题为什么都能用乘法计算”来唤起学生对乘法意义的认知，让学生在信息解读、对比联系中明白解决实际问题的依据是运算的意义。

（二）类推中深化模型

新课标倡导的新型学习方式之一是在推理、探究中学习。但由于家庭、条件等环境因素的影响，学生的现实起点存在明显差异。因此，教师在教学时要根据学生已有的知识经验借助教具进行直观教学，引导学生在推理中展开新知学习，通过知识间的迁移类推建立多位数乘一位数的口算模型，从形式上降低学生学习的难度。

【教学片段二】

笔者让学生尝试在计数器上表示“20×3，200×3”，引导学生思考：“为什么两次都拨了3个2？如果再拨3个2，可以怎么拨？用哪个算式表示？”

根据学生的回答，笔者呈现板书后组织学生观察3道算式的相同之处和不同之处。

在讨论中小结：虽然计数单位不同，但都是利用计数单位把整十、整百、整千数转化成表内乘法解决。

前测数据表明学生的认知程度存在很大差异，所以很难直观理解口算乘法的算理、算法。故笔者借助计数器这一直观模型让学生经历从“20×3”到“200×3”再到“2000×3”的探究过程。同时让学生在“2个十乘3是6个十，就是60”这一已有经验的基础上通过看数位、拨珠子、说意义等活动帮助学生厘清算理，逐步建立“整十、整百、整千数乘一位数”的口算模型。

（三）操作中勾联算理

【教学片段三】

笔者让学生尝试通过画一画、写一写证明12×3=36。学生分别以加法算式（见图1）、画图（见图2）、分步计算（见图3）来表述自己的想法。在学生发表见解后，笔者让学生尝试在图中找到10×3（3个10），2×3（3个2）分别在哪一部分。

图1

图2

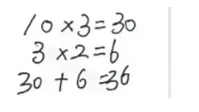
图3

三年级学生还处于具象思维阶段，对纯文字算理的表述和理解存在困难。因此，笔者让学生经历“画一画、写一写、圈一圈”等操作，借助小棒图帮助其理解多元表征背后的共性，特设计了三次勾联：一是结合小棒图将12+12+12=36和12×3=36进行联系，回顾乘法是加法的简便运算；二是将分步计算和小棒图进行沟通，引导学生圈出小棒图每一部分对应的算式，通过图式一一对应帮助学生直观理解算理；三是在理解小棒图的基础上，再次对多种方法进行勾联和归纳。三次横向勾联都是聚焦多元表征背后的算理“把12看成几个计数单位分别乘3”。在操作中建构两位数乘一位数的多种算法，使知识形成一个结构化体系，便于学生对算理的理解。

（四）对比中抽象算法

算法是对计算过程的抽象和概括，算法和运算技能的形成不是一步到位的，教师需要给予学生充分的比较、思考、交流的时间和空间，让学生在感受、讨论的基础上进行计算方法的对比沟通，进而抽象出算法。

【教学片段四】

师：观察算式“20×3，200×3，2000×3”，这3道算式有什么异同点？组内讨论比较得出整十、整百、整千数乘一位数的计算方法。

【教学片段五】

师：（口述）每人玩一次旋转木马5元、一次登月火箭8元，两项共13元，3个人一共要多少钱？每人玩一次旋转木马5元、一次过山车12元，两项共17元，3个人一共要多少钱？

让学生试着口算13×3、17×3，思考两位数乘一位数要注意什么，123×3该怎么算。对比“13×3，17×3，123×3”3题，小结多位数乘一位数的计算方法。

低年级学生不善于用数学术语来表述算法，总结、概括的能力也较弱。为此，笔者设计了三次对比：一是将整十、整百、整千数乘一位数进行纵向对比得出计算方法；二是将两位数乘一位数口算（进位和不进位）进行横向对比，让学生在计算中注意进位、积累算法经验；三是在“去情境”状态下将两位数乘一位数和多位数乘一位数进行对比，引导学生用数学术语抽象运算方法，即把多位数分成几个百、几个十和几个一乘一位数，再把乘得的结果相加。三次对比让学生经历了从“分”到“合”的计算过程、从直观理解到抽象理解的内化过程、从已经学的到将要学的迁移过程，不仅提升了学生对运算结构的认知，还使运算知识得以生长和内化。

三、回顾进程，梳理反思方致远

（一）合理选材，促进整体建构

第一次试教时，利用2022年版教材中的游乐园情境图教学，但5个游乐项目的价格使学生回答的算式多而杂，不利于后续教学展开。第二次尝试精简游乐项目，修改个别数据展开教学，算理、算法的建构呈现出比较好的效果。所以，笔者认为今后在选取材料时需要思考以下几点：一是所选材料是否贴近学生生活；二是所选材料能否利于后续教学；三是所选材料是否有助于知识间的整体建构。

（二）注重感知，夯实算理算法

第一次教学“20×3，200×3，2000×3”时，要求学生观察3个算式并归纳算理、算法，难度太大以致学生表达不到位，甚至含混不清。再次教学时，选用计数器这一模型让学生在观察操作、联系对比中夯实算理、算法，效果明显得到改善。因此，笔者认为今后在教学计算课时，可以从以下几个方面着手：一是借助多元表征直观地感知；二是借助观察操作有目的地感知；三是借助联系对比深入地感知。

综上所述，算理的理解和算法的形成是一个循序渐进的过程。要想让学生更好地明晰口算乘法的算理、算法，笔者认为教师要立足学生认知起点，以生活情境为背景、活动探究为脚手架，在类推、操作和对比中感知、建立运算模型，让学生在理解运算意义和算理的过程中掌握算法。