关注过程，让概念教学走向“精致”

丁超林

［摘  要］ 在概念教学中，“精致”的实质是：通过可操作过程，对概念的内涵与外延进行深度剖析。以“认识几分之一”的教学为例，基于对小学生心理的多重考虑，运用问题情境、变式情境、反例比较、动手操作等策略，让概念教学走向“精致”。

［关键词］ 关注过程；概念教学；走向“精致”

新课程改革形势下，广大教师越发重视概念形成阶段的“精致”。这需要教师详尽而深度地加工概念的内涵与外延，具体地界定概念的各个要素，让学生建立清晰的概念表象，进一步完善思维模型。

众所周知，概念教学历来是重难点，其主要原因在于概念的高度抽象性。在概念教学中，“精致”的实质是：通过可操作过程，达到对概念的内涵与外延进行深度剖析。基于对小学生心理的多重考虑，运用问题情境、变式情境、反例比较、动手操作等策略，能让概念教学走向“精致”。下面，笔者结合“认识几分之一”的教学实践，谈谈如何关注过程，让概念教学走向“精致”。

一、问题情境，让概念的内涵更显性

从几分之一的定义中，可以看出它比较难理解，如何才能使其更加“显性”呢？通过独特问题情境的引领，可以激发学生原有的认知经验，通过生活经验与新知的适切沟通，激起学生的探究兴趣，自然促成学生对概念的理解和认识。

教学片段1

师：今天猴妈妈给2只小猴带来了最爱吃的水蜜桃（视频展示）。

师：猴妈妈要把1个甜甜的水蜜桃平均分给2只小猴，每只小猴可以分到多少？几分之几？说一说思考的过程。

生1：分到一半，就是二分之一，也就是将1个桃平均分2份，每一份是1个桃的。

师：吃完了半个，小猴们意犹未尽，猴妈妈又从厨房取来了1盘水蜜桃。（视频展示一盘用毛巾掩盖着的水蜜桃）

师：（追问）若将这1盘桃平均分给2只小猴，每只小猴又可以分到多少？几分之几？说一说思考的过程。

生2：将1盘桃平均分2份，每一份是1盘桃的。

师：现在猴妈妈掀开毛巾，哇！里面有2个桃，每只小猴可以分到多少？会怎么分？

学生七嘴八舌。

师：（边示范边解说）我们可以先将2个桃看作一个整体，用集合圈将它们一起圈起来，再平均分成2份，用一条虚线将圈起的桃子分成2份，每一份就是这1盘桃的。

师：这一份就是它的，另一份呢？

生（齐）：也是它的。

师：谁能说一说刚才老师是怎样分的？

学生先自告奋勇地阐述，再同桌两人相互阐述。

师：倘若猴妈妈掀开毛巾，里面是4个桃，又该怎么分给2只小猴呢？请大家独立思考，并在草稿纸上按照刚才的步骤圈分。

学生自主尝试。

师：（行间巡回指导，发现了和两种答案）咦！到底哪一种答案正确呢？请各学习小组合作讨论。

学生展开火热的辩论后，很快有了统一的认识。

师：倘若盘子里是6个桃，该如何分呢？

学生在作业本上熟练地圈分。

师：我们一起来观察，刚才的三个画面，第一次是2个桃，第二次是4个桃，第三次是6个桃，三次分桃的个数各不相同，而其中一份均用表示，这是为什么呢？

生3：因为都是平均分成2份。

师：非常好！显而易见，不管总数是多少，只需将其视为一个整体，平均分成2份，每份都是它的。

思考：一般来说，小学生认识事物都是从直观感知开始的，并在多感官參与的刺激下形成深刻表象，这说明只要有了一定的感性积累，就能逐步上升到理性认识。教学片段1中，教师将概念与学生生活经验进行整合，创设拾级而上的问题情境，使得学生始终形成“多个桃视为一个整体”的意识，促进学生建立起清晰而深刻的整体表象。

二、变式情境，让概念的本质更清晰

数学概念比较抽象，各种数学概念的描述，不但枯燥，而且无味，既不像美术那样具有直观性，又不像语文那样具有描述性，更不像体育那样具有参与性。数学概念的本质，从具体到一般，从直观到抽象，从内涵到外延，需要学生多层次、多方位、多角度地领悟。另外，要使抽象的数学概念变得有滋有味，变得生动、具体、易懂，就得从生活中挖掘数学素材，从日常生活中发现数学知识，领着学生走进数学，引导学生对数学情境进行变式。

所谓的变式，就是通过不断变化事物的非本质属性，引发学生的思考，以达到凸显其本质属性的目的。对于概念教学而言，全面而充分的变式，可以引领学生感知概念在各种情境中的情形，以获得对概念更加深刻的理解和认识。因此，教师可以创设开放式的问题情境，让学生在比较中鉴别，在冲突中完善，在变式情境中明晰概念的本质。

关于变式情境，通常可抓住三个时机。一是抓住概念引入的时机，概念引入时变式，就是先将数学概念还原到现实情境中，再通过变式移植数学概念的本质属性，使现实情境数学化。二是抓住概念形成的时机，概念形成时变式，就是先对学生的首次感知进行强化刺激，再为学生架构一个支撑点，以点带面，沟通新旧数学概念间的联系。三是抓住概念巩固的时机，概念巩固时变式，就是先为学生提供常态的、标准的、典型的变式材料，再让学生去辨析比较，以防学生由于思维定式而产生负面影响。

教学片段2

师：又有一只小猴回来了，猴妈妈掀开毛巾，里面是6个桃，现在想平均分给3只小猴，每只小猴可得这盘桃的几分之几？请大家先在作业纸上尝试，然后交流。

生1：。

师：为什么是呢？这一份是这盘桃的，那一份呢？还有一份呢？

生2：每一份都是这盘桃的。

师：（出示视频，让学生观察）若又来了3只小猴，现在需要将这6个桃平均分成6份，每一份又是它的几分之几？请大家再一次尝试，并说一说是怎样分的。

学生尝试后，得出结果。

师：请大家回忆刚才的情景，同样是6个水蜜桃，为什么每一份所表示的分数却各不相同呢？

生3：因为平均分的份数各不相同。

师：非常好，那么如果盘子里有8个桃，你该如何表示出它的呢？

生4：将其平均分成2份。

师：真棒！那么若盘子里有24个桃，你会表示出它的吗？

生5：将其平均分成8份。

……

师：综上所述，确定这盘桃的几分之一，关键在于平均分成了几份。

思考：在教学片段2中，教师以变式情境为指导，引领学生比较“都是6个桃的情形下，为什么每一份表示的分数不一样”及感知“盘中有8个桃如何表示其”“盘中有24个桃如何表示其”等情形。如此的一个又一个变式情境，让学生的认知从困惑，逐步走向清晰和深刻，从而获得一般性理解，进而悄然地领悟几分之一的概念内涵。

三、反例比较，让概念的认识更深入

反例，顾名思义，指和正例相反的例子。在数学教学中，恰当地引入具有针对性的反例，可帮助学生提升数学思维，突破教学重难点，更深入地认识所学的数学概念。对此，教师应努力做到“三个巧用”。

一是巧用反例，消除概念的误区。对小学生而言，抽象思维能力还未完全成熟，在认识数学概念时，常常因出现曲解，而产生概念的误区。巧用反例，可让学生在辨析、比较和探究中发现错误、认识错误、纠正错误，从而正确、全面、深入地认识数学概念，消除数学概念的误区。

二是巧用反例，突破概念的難点。从小学生的实际情况看，数学思维还存在着相当的局限性，容易受原有知识经验和以往教学活动的影响，容易被数学问题的表象所迷惑，容易出现数学概念认识上的模糊，容易产生消极的思维定式。巧用反例，可以引起学生的有意注意，助推学生克服思维定式，从而拨乱反正，明晰数学概念的本质属性，突破数学概念的难点。

三是巧用反例，重获概念的认知。现行教材中的例子，通常都是正例。从一分为二的角度考虑，正例虽好，但容易导致学生生搬硬套，束缚学生的思维，不利于培养学生思维的灵活性。巧用反例，借助学生出现的典型错例，特别是学生在现场出现的典型错例，可以促进学生远离知识的负迀移，重组数学认知结构，重获概念的认知。

从教学片段1和教学片段2可以看出，学生已经能比较准确地理解“几分之一”的概念了。那么，对于数学概念“几分之一”的教学，是否就到此为止呢？显然不能，若想让学生对“几分之一”的认识更加深入，教师还需要提供反例，引导学生在比较中思辨，在思辨中深化，使其对“几分之一”这一数学概念的认识更加深入。

教学片段3

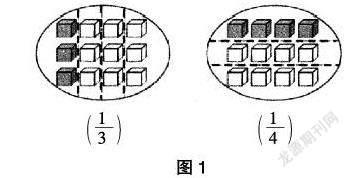
问题：如图1，以下分数所表示的涂色部分是否正确？为什么？

思考：在教学片段3中，为了激发学生的思维，教师提供了变化概念本质属性的反例，引起学生的对比与思辨，使学生通过辨析，形成对概念本质属性的深刻理解。

四、动手操作，让概念的建构更完善

在概念形成中，教师还需要积极为学生提供动手操作的机会，以直观素材为支撑，让学生在做思共生中经历知识的发生、形成和发展，体验自主获取概念的成功乐趣，使得概念的建构更完善。

小学生的思维，总是以形象思维为主。数学概念的形成，一般的流程是：事例→表象→概念→应用。动手操作，在数学概念的形成过程中，有其重要的支撑作用。学习数学概念时，充分发挥动手操作的支撑作用，能降低学生获取数学概念的难度，清晰认识数学概念形成的过程，从而深刻理解数学概念，使数学概念的学习过程生动、活泼、有趣，进而大大提高学生学习数学概念的效率。为了充分发挥动手操作的支撑作用，让数学概念的建构更完善，应想方设法帮助学生架构好“三个支撑点”。

第一个支撑点，让学生在数学概念的“感知”阶段，借助动手操作“建立表象”。数学概念的“感知”阶段，其实就是“事例→表象”的阶段。在这一阶段，应让学生投身直观性的学习活动之中，初步认识数学概念。可以凭借所学内容的特点，编拟相应的操作步骤，让学生有序操作，唤起学生已有的经验，逐步感知具体事例，不断获取感性认识，寻找事物的本质属性。

第二个支撑点，让学生在数学概念的“理解”阶段，借助动手操作“感悟内涵”。数学概念的“理解”阶段，其实就是“表象→概念”的阶段。在这一阶段，应让学生投身感知活动后，获得感性认识，对形成的表象进行总结、提炼和概括，并对其属性进行分析、研究和比较，把共同的本质特征抽象出来。理解概念的本质内涵，是这一阶段的重心。因为小学生的抽象分析能力还比较弱，所以需要借助动手操作，促使学生理解数学概念的本质内涵。

第三个支撑点，让学生在数学概念的“应用”阶段，借助动手操作“拓展升华”。数学概念的“应用”阶段，其实就是“概念→应用”的阶段。在这一阶段，应让学生在理解数学概念的本质内涵后，先获得数学概念的模型，再从抽象回到具象中，对数学概念进行应用拓展。学生在对数学概念的应用拓展中，既能借助正反两方面的事例，检验数学概念的外延，又能将数学概念推广到同类事物中，实施沟通、联系和总结，从而形成数学概念系统。

教学片段4

师：现在我们一起来玩一个游戏好不好？这个游戏叫“分小棒”，下面就请同桌两人一组用12根小棒进行游戏。先请一名同学来做个示范，谁愿意呢？

师：（随机点名）请你先分出这些小棒的，再说一说你是如何分的？

学生按照要求动手操作，展开游戏。

……

师：在这个“分小棒”游戏中，大家明白了什么？

生（齐）：将这些小棒（一共12根）平均分成几份，其中的一份，就是它的几分之一。

思考：在教学片段4中，教师创意地设计“分小棒”的游戏，以学生喜爱的这一动手操作活动，引导学生分析、比较、综合、概括和抽象，以固化学生的认识，促进学生深刻理解分数的本质意义，真正达到了在操作中发展思维，在操作中完善认知结构的目的。

总之，教师需要引领学生走向知识，让学生在概念“精致”的过程中，收获无限的智慧与启迪。从教学片段1到教学片段4，教师以问题直击概念本质，以变式和反例促使学生的认识从具象走向抽象，以做思共生引领学生从浅层走向深层，让学生不知不觉地完成了对几分之一的建构，获取了丰富的数学活动经验。这既是概念“精致”的过程，又是思维模型不断完善的过程，更是概念教学中凸显“学为中心”的关键所在。