深度学习：在“一题一课”中让学习真正发生

周良

［摘  要］ “一题一课”，是通过一个数学学习主题或一道习题的深入研究，组织学生开展相关的数学探究活动。深度学习旨在引发学生积极主动参与学习过程，深度探索学科中的关键问题。深度学习是在更高层次上的知识回归与整合、技能训练与提高。学生围绕着具有挑战性的学习主题，积极参与，体验成功，获得发展，提高数学素养。

［关键词］ 一题一课；深度学习；关键问题；数学素养

与传统课堂教学相比，“一题一课”无疑是比较另类的课堂教学，尤其是在小学阶段，这样的课堂似乎不常見。但是作为对传统课堂教学的有益补充，“一题一课”无疑有其独特的、不可替代的作用。它不是学科知识和技能的简单重复，而是在更高层次上的知识回归与整合、技能训练与提高，其主要表现为知识结构化、问题思维深刻化、学科能力个性化。郑毓信教授将“深度学习”与“浅度学习”进行对比时指出，浅度学习主要依靠死记硬背与机械模仿，只满足于内容的简单积累，最终造成了“知识碎片化”的现象［１］，而深度学习则有效避免了学习的肤浅化。通过实践探索，笔者把“一题一课”作为实现深度学习的一个重要实践研究内容，取得了很好的教学效果。

一、“一题”的素材选择

《义务教育数学课程标准（2022年版）》指出：“小学数学教学任务之一是培养学生的思维能力。”在日常教学中，教师要根据学生差异，设计由浅入深的作业题，特别是要调动学生思维，在一道题的认知冲突中逐步提升学生的数学思维品质。

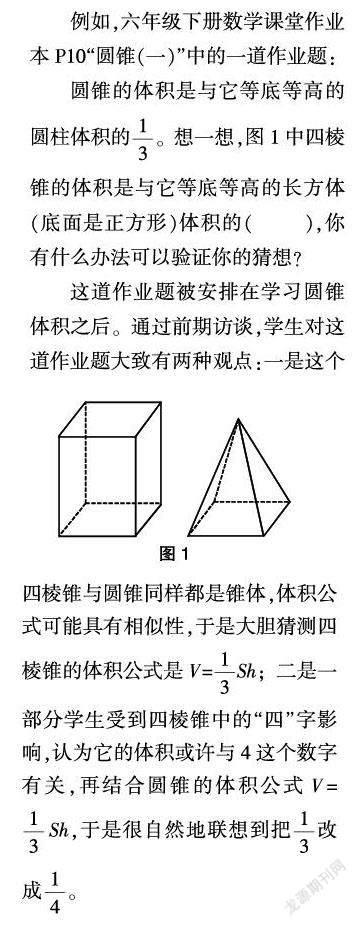
例如，六年级下册数学课堂作业本P10“圆锥（一）”中的一道作业题：

这样的作业题可实践，也可推理论证，它既是学生容易做错的题，又能让学生动手又动脑，无疑是“一题”的绝佳素材。

二、“一课”初长成

1. 错有所值，何错之有

暂且不论教师能不能给出一种除实物演示实验的方法之外学生可接受的数学证明，仅部分学生认为四棱锥的底边是正方形，有4条边，或许结论与数字“4”有关，进而与圆锥体积公式类比联想得到V=Sh，就让人欣赏不已。这样的想法尽管是错误的，但也是一种很了不起的发明创造。不过，欣赏归欣赏，现在的问题是教师能不能用一种有效的手段“扳回”这些学生的“伟大”想法，进而让学生的数学思维得到有效的训练呢？这里的“扳回”不是教师的“横柴入灶”，而是要在顺应学生思维的基础上，在教师的有效引导下，让学生发现自己的错误，进而否定自己的想法。教师能否在此问题上做一点点有效的“突围”呢？

2. 将错就错，错中悟理

至此，学生都表示认可，同时露出既惊讶又欣喜的表情。

笔者顺应学生的原生态想法，进而引申出荒谬的结论，使学生产生了强烈的认知冲突，并进行自我的否定。

师：这道题给你怎样的启发？

生3：我原以为四棱锥的体积可能与底边的边数有关，但是用“夸张再夸张”的方法，从四棱锥一直推到圆锥，便得出了错误的结论。可见，充分想象对我理解事物的本质很有帮助。

师：是的，想象力很重要，大家遇到问题时要学会多思考，有时从“夸张再夸张”的角度去思考问题，或许就会有特殊的、意想不到的结果产生。

把语文中的“夸张”的修辞方法运用到数学上，用“夸张再夸张”的方法创造出一个让学生感到亲切的、可接受的数学思想方法的名词。出于有效联系学生已有的基本学习经验和尊重小学生的认知特点的考虑，笔者有意回避了对学生来说有些晦涩难懂的“极限”等数学名词。

三、“一课”再教学

1. 看似完美，实有隐忧

上述看似完美的课堂教学，实存隐忧。上面的教学中否定了四棱锥的体积V=Sh，进而自动认为V=Sh是正确的。但是去“伪”未必存“真”，这种非此即彼的思考方式本身就存在一个逻辑错误。解决这个问题的关键在于如何从数学的角度来证明V=Sh是四棱锥的体积公式。这样最具说服力，但问题也随之而来。其一，有没有必要从数学的角度来证明？其二，即便能证明，怎么证明？学生能听懂吗？这是因为如何将思维含量很高的数学素材变成有效的教学素材是个大问题。换句话说，如何用小学六年级学生能接受的方式，比较数学化地证明四棱锥的体积，是解决这个问题的一个重要思考途径。

回到课本中，关于圆锥体积公式的推导，现行的所有教材都是采用实物演示实验的方法，得出等底等高的圆锥的体积是圆柱体积的。但是用实物演示实验的方法本身就缺乏说服力，先不说演示实验本身就存在误差，即便实验确实得出了等底等高的圆锥的体积是圆柱体积的，那也只能说明做实验的那组圆锥和圆柱的实验器材是符合这个结论的，而这并不能证明所有的等底等高的圆锥和圆柱之间都存在这样的关系。当然，教材这样安排肯定充分考虑到了小学生的认知特点，是在深刻性与生动性之间寻找了一个中间地带，是一种不得已而为之的折中的办法。如果沿用教材的思路，那么对于这道作业题而言，最好的解决方法也就是用实物演示实验的方法。

可是，当教师面向全体学生进行教学时，怎能忽略那些具有独立钻研精神，对数学学有余力且好问为什么的学生的能力培养呢？更何况这也是因材施教的需要和教师的职责所在。事实上，早在学习圆锥体积时，就有“好事”学生问笔者如何用剪拼的方法来推导圆锥的体积公式。笔者当时只随口回了一句“以后会学”，便打发了学生。现在回想起来，学生有此想法必有其背后的原因：从平行四边形面积的推导到圆面积的推导再到圆柱体积的推导，都是通过剪拼的方法将原图形转化成规则图形进行思考的。那么，对于圆锥的体积，学生自然而然就会想到是否也能通过剪拼的方法进行转化。这样的想法是学生内心深处对知识探究的渴望与追求，只怪笔者当时处理得过于草率了。如今，笔者不得不理性地思考该如何正确对待这些学生内心深处对知识探索的渴望与追求。

2. 峰回路转，极限渗透

因此，笔者的想法是：对于该题，可以进行个性化处理，无须对每个学生都做要求。由此，笔者有了对此题可行性操作的新思考。

笔者在六年级的数学拓展课上采用小步骤具象化操作，效果较好。步骤如下：

（1）借助类比，转化成长方体。

回忆：推导圆面积时，我们把圆面积等分成16份，并转化成了一个近似的长方形；推导圆柱体积时，我们将其转化成近似的长方体。现在能不能把四棱锥也转化成我们熟悉的立体图形呢？借助多媒体演示，用平行于四棱锥底面的平面去“切”这个四棱锥，把这个四棱锥平均“切”成很多份，只要“切”的次数足够多，每个“薄片”就可以近似地看成是一个长方体。把这么多长方体的体积相加，就是这个四棱锥的体积了。

（2）用辅助线画图，明确各个近似长方体底面的边长。

学生用平行于四棱锥底面的平面去“切”这个四棱锥，从简单的二等分、三等分、四等分开始，配合画辅助线的方式找到规律，进而很顺利地得到当把这个四棱锥等分成16份时，它的底边长分别是a，a，a，…，a。具体见图3。

（3）极限渗透，求出近似值。

四棱锥等分成16份后，每一份可以近似地看成一个小长方体。小长方体的底面是一个正方形，边长依次为a，a，a，…，a，高都是h。每一个小长方体的体积相加，就是近似的四棱锥的体积了。

学生利用计算器进行分工合作，得出以上计算结果。虽然等分的份数不够多，但从计算的结果来看，已经很接近正确答案了。学生在学习圆面积时把圆等分成若干份，可转化成一个近似的长方形，当等分的份数越多，也就越接近长方形。基于这样的学习经验，学生借助类比想象：如果四棱锥等分的份数越多，计算出的体积是不是就越接近正确答案呢？借助多媒体演示，教师可以切分得更细，让学生直观感受到随着等分的份数逐渐增加，其体积越来越接近a2h。

事实上，教学进行到这里，并没有严格证明四棱锥的体积公式，最多是越来越接近a2h。这就如同学生在研究圆面积时教师也只能把圆转化成一个近似的长方形一样。这是小学生特定的认知限制所致，教师不必苛求。不可否定的是，上面的研究充分调动了学生已有的学习经验，同时还渗透了一些基本的数学思想。

四、“一题一课”的研究方向

大脑不是一个需要被填满的容器，而是一个需要被点燃的火把。教育心理学界普遍认为，元认知在整个智力活动中处于支配地位，对整个活动起控制调节作用，元认知在数学认知过程中具有重要作用［２］。激发学生学习兴趣，提升学生核心素养，成为“一题一课”研究的最终落脚点。

“一题一课”的内容要基于教材但又不限于教材，要注重学生实际与数学核心素养生长点的契合。其内容的选择可以是教材中富有内涵的习题、学生学习中的疑难问题以及其他有探究价值的学习材料等。选材要具有一定的探索性，要能让学生深度参与到学习中去。

“一题一课”要体现深度学习的过程。深度学习是一个有意义地运用知识的过程，包含六个方面的策略：问题解决、创见、决策、实验、调研和系统分析。学生能否灵活运用这些策略是教师判断学生是否进行了深度学习的依据。

五、“一题一课”的实施要点

如何提高“一题一课”教学的针对性和实效性？

1. 切忌就题论题

“一题一课”教学关键是要突出学生的数学思维能力。数学思维能力的提升应当是“一题一课”的精髓。数学思维的训练，是数学教育的本原目标，数学思维能力是高效数学学习的根本特征［３］。

教师要有目的地创设让学生勇于质疑问难的空间与时间，帮助学生分析问题、解决问题，让学生真正享受“做数学”的过程，让学生有时间、有机会对自己的思维活动进行对比与反思，提高数学素养。

2. 提高数学教师的专业素养

真如张景中院士所说，小学数学具有“小儿科，大学问”的特质。小学数学教师的专业素养，尤其是小学数学教师本体性知识的缺失，在一定程度上制约了小學数学教学质量的提高。像上面的这道数学作业题，教师引导学生科学探究的过程一定会植根于学生的内心深处，其在培养学生自我反思、科学严谨的学习态度，有机渗透数学思想等方面的价值要远远高于解答出这道题目本身。

3. 科学合理地看待学生差异

教师要清楚地认识到每个学生的数学理解能力和接受能力是不一样的，不必也不可能用同一标准去要求每一个学生。分层教学、因材施教，是基本的教学常识。科学合理地运用学生的差异，促进师生之间、生生之间的互相学习是课堂教学有效生成的手段之一。

这样的“一题一课”教学犹如做小课题一般，让学生感受到了数学之美。只有学科本身的魅力才会让学生产生持久的学习兴趣，而这恰恰也是当前有些浮躁的教学中所缺少的学科特性。“一题一课”是深度学习的实践路径，能让学习真正发生。

参考文献：

［１］ 郑毓信. “数学深度教学”的理论与实践［Ｊ］. 数学教育学报，２０１９，２８（０５）：２４－３２.

［２］ 欧慧谋，唐剑岚. 国内数学元认知的研究与思考［Ｊ］. 课程·教材·教法，２０１２，３２（０５）：５８－６１.

［３］ 史可富，孙志慧，李冬胜. 高效数学学习的学生心理特征模型［Ｊ］. 数学教育学报，２００６（０４）：７９－８２.