力促“数”“形”相融，发展几何直观

郑名银

［摘  要］ 针对学生在运用数学公式解决图形问题时存在的“数”与“形”脱节的现象，文章以三年级“长方形的面积公式推导”为切入点，强调数学知识教学与学生生活经验的联系，引导学生经历观察、实验、分析、概括等活动过程，渗透数形结合思想；通过展现“数”与“形”动态相融的过程，发展学生的几何直观，既促进了学生的认知理解与思维融通，又帮助学生积累了基本的活动经验，更是培养了学生的空间观念，实现学生关键能力的提升。

［关键词］ 长方形的面积；数形结合；几何直观；空间观念

《义务教育数学课程标准（2022年版）》指出，“图形与几何”是学生感知生活空间的重要工具，也是描述图形特征并进行沟通与交流的重要途径。学生在学习“图形与几何”知识时，除了要能清晰地描述图形的运动和变化，还要能灵活地应用数学知识解决生活中的实际问题，进而促进自身的空间观念的发展。

教学实践发现，当学生遇到求解有关图形面积、图形体积题目时，往往先是回忆对应的计算公式，并根据已知条件完成数据代入与计算，如解决有关“长方形的面积”问题时，学生先会在大脑中提取面积计算公式：长方形的面积=长×宽，然后找到问题中长和宽的数值，最后依据公式计算面积大小。这样的解答，只是为了得到一个结果，图形在这里起不到任何辅助知识理解的作用，“数”与“形”完全被割裂，长此以往，不利于学生空间观念的培养，更是降低了学生数学学习的兴趣。

一、基于教材，辨析数学认知误区

图形的面积计算本质就是对二维面积的度量，三年级学生从对一维长度的度量到对二维面积的度量，在认知上是一次质的飞跃。为了帮助学生充分感悟二维面积的度量本质，人教版教材设计了贴近学生实际的生活素材，引导学生经历观察、辨析等探究性体验活动，力求帮助学生厘清面积概念的含义，体会“统一面积单位”的必要性，在形成面积单位表象的基础上，深刻理解“长方形的面积”的计算方法。

“长方形的面积计算公式推导”的学习，是学习其他平面图形面积公式的基础，为研究其他平面图形面积公式提供了基本原理和方法［１］。教学过程中，学生经历初步感知、合作学习、归纳概括等探究活动，符合学生的认知规律，也激发了学生的探究欲望，为学生理解和掌握长方形的面积计算方法提供了活动经验，但为什么在后续的“面积计算公式”运用中会出现“套用公式”“数形脱节”等现象呢？究其原因，笔者认为有以下两点：

（一）断层式认知

在“长方形的面积计算公式推导”的起始阶段，学生通过用多个面积单位的小正方形测量长方形，发现小正方形个数恰好是长方形的面积数，这为后续厘清“长方形的面积与长、宽之间的关系”奠定了基础。然而，这样的探究过程并未真正演绎因果联系，只是恰好符合规律，很多时候，学生的数学思维在认知上是断层的，导致学生对图形的面积计算变成了公式的记忆与运用，却难以将图形面积概念的本质与面积计算公式进行融通。

（二）误导式建构

在研究“长方形的面积与长、宽之间的关系”过程中，开始是利用若干个1平方厘米的小正方形对大长方形进行覆盖，初步感受“一行有几个，有这样的几行”的模型，最终归纳得到长方形的面积计算公式。但学生在求表面是长方形的物体（如：课桌、铅笔盒）表面积时，又要先分别测量一维的长度和宽度，再计算二维的面积，这就让原本的面积问题变成了数值计算问题，导致学生对面积的概念理解和二维建构始终是不到位的。

二、认知理解，体验数学实验任务

张奠宙教授曾提出，“面积是小学数学‘图形与几何’领域的‘图形测量’部分的概念，它具有‘数’的基本属性，即可以找到一个合适的数对其属性进行描述”。他认为，数方格的过程就蕴含了面积的“有限可加性”这一基本特征。教学时，教师可以引导学生从“线动成面”这一理念来认识什么是面积，让图形“动起来”，充分体验“面积”的内涵。

在“长方形的面积计算”教学过程中，学生早已知道了长方形面积公式，但对于“长方形的面积公式为什么是‘长×宽’，为什么测量的是长度而算出来的却是面积，如何帮助学生更深刻地理解面积计算公式”等问题，还需要再思考、再研究。鉴于以上分析，笔者尝试如下教学，以供参考。

（一）探究学习

教学实践发现，要促使学生理解“长度乘长度就等于面积”是有一定难度的。教材在设计“长方形的面积计算公式推导”的教学环节时，充分利用了直观演示的方法，帮助学生感知“长几厘米，每行就摆几个小正方形，宽几厘米，就摆几行”的原理。学生经历从一维的长度数值转化为二维的面积单位个数的过程，从“长乘宽”的公式中架构长方形面积的过程表象。基于教材内容与学生已有经验，开展如下教学：

（1）直观呈现学习情境，引导学生尝试用数格子法或用面积单位法进行面积的测量，并计算长方形的面积。（2）经历两种面积计算的方法：一种是数个数法，“1个1个地摆，共摆了15个，面积就是15平方厘米”；另一种是乘法计算法，“每行摆５个，就是５平方厘米，共摆了３行，面积５×３等于１５平方厘米”。（３）在此基础上，组织学生开展用多个面积单位拼摆长方形的活动，并用表格记录对应的长、宽和面积。（４）观察与分析面积单位的个数与长、宽之间的关系，归纳概括得到长方形的面积计算公式。

（二）认知延伸

每一次的课堂教学实践，都是师生共同经历思维碰撞、智慧生成的过程。这就要求我们在教学某一知识点时，提前精心设计教学内容，做到瞻前顾后，把握教学的“度”。三年级“长方形面积的计算”知识的学习，其本质是“度量法”的渗透，即：理解“长方形的面积”为什么是用“长×宽”来计算的。从长度到面积的学习，空间形式的认知是一次飞跃，容易造成学生对图形认识和测量上的混淆。因此，需要增设面积的拓展内容，借助数形结合、比较辨析、知识梳理等活动过程，幫助学生理解“长方形面积计算”的本质。

1. 动态演示

对小学三年级的学生而言，空间观念的建构，一方面需要教师在教学过程中进行有意识培养，另一方面也离不开学生自身对生活空间的观察、感悟等活动经验的积累。借助“几何画板”，辅助数学课堂教学，改变了教师讲授和学生被动学习的传统教学模式，呈现图形的动态演示过程，从不同的角度分析数学问题，促进学生的思维发展。以探究“长7cm、宽5cm的长方形面积计算”为例，尝试如下教学：

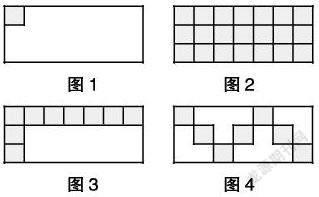
（１）学生猜测：根据已有认知，认为面积是7×5=35cm2（如图1）。（2）直观教学：利用“几何画板”软件，对图形进行动态演示，观察并分析图形的变化情况，a. 一共摆了21个，每个面积是1cm2，长方形的面积是1×21=21cm2（如图2）；b. 每一行有7个小正方形，一组7个面积是7cm2，有这样的三组，那就是3个7cm2，列式为7×3=21cm2（如图3）；c. 观察变式图形，分析并开展讨论，达成共识，长方形的面积是7×3=21cm2（如圖4）。

2. 课件推导

学生经历以上环节的学习后，自然地会由经验积累联想到公式背后的推导过程，教师需要引导学生结合运算的意义理解，寻找面积公式推导的依据［２］。教师根据学生的已有认知，借助课件辅助教学。学生经历“平移”“累加”等直观感知过程，想象、体会整个长方形的形成过程，理解“线动成面”的内涵，进而进一步体会长方形的面积计算公式的概念本质。借助课件，推导“长方形的面积计算公式”：

（１）课件出示：将一条长为７ｃｍ的“线段”逐渐变粗，最终转变成宽度是1cm的“线段”，这条“线段”的面积是7cm2（如图5）。（2）将“线段”向下平移，形成2条这样的“线段”，得到的图形面积就是2个7cm2，列式为7×2（如图6）。（3）“线段”继续向下平移，形成3条长为7cm的“线段”，所占平面的大小是3个7cm2，列式为7×3（如图7）。

（三）思考总结

传统教学模式下，面对“长方形的面积计算”这一教学内容，尽管教师引导学生采用了自主探究、合作交流等学习方式，纵然追寻着渐进式的探究学习，但仍旧不利于学生思维能力的提升，“新课后的知识补充”还需要另加课时，但也不一定会达到预期的教学效果。基于教材内容和学生认知水平，教师在开展基础内容教学时，借助几何直观，动态呈现图形的变化情况，提升学生的空间想象能力。

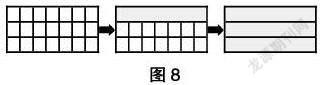
回顾小结：将每一行看作是一条“粗线段”，每条“粗线段”的面积是7cm2，3条“粗线段”累加的面积就是整个长方形的面积（如图8），即3个7平方厘米，列式为7cm2×3=21cm2。因此，长7cm、宽3cm的长方形，它的面积计算列示为7×3，进一步解释了长方形的面积可以用“长×宽”来计算。

课堂最后，教师提问：“长方形的面积=长×宽”就是我们学过的哪个数量关系式？学生思考，回答：每份数×份数=总数。课件出示问题：每份数就是（宽为1cm的“线段”的面积），份数就是（宽为1cm的“线段”的数量），总数就是（面积），并引导学生尝试回答、讨论。

当学生的思维经历从一维运动到二维运动的演变之后，下一次面对某个平面图形的面积计算时，其脑海中呈现的就是该图形的动态形成过程，即：一条有宽度的“线段”的平移，并将得到的几条有宽度的“线段”进行累加，而对应的面积计算公式就转换为求“几个几”的和，也就是“每份数×份数=总数”。如此一来，面积计算公式就与平面图形动态融通了，既省去了学生记忆公式的烦恼，又培养了学生的空间观念。

三、收获启示，促进数学思维养成

几何图形的本质就是“点的积累、线的积累、面的积累”，也就是求“几个几”累加的和是多少。教学实践发现，要促使学生深入地掌握有关“图形与几何”领域的知识，需要借助几何直观，抓住问题的本质，不但有助于学生理解数学的概念，而且有利于发展学生的数学思维。

（一）抓住本质，实现“数”“形”相融

儿童的认知结构是通过对问题的同化与顺应而逐步建构起来的，尤其是思维的发展需要在“平衡—不平衡—新的平衡”的演变过程中得以不断的丰富与发展。通过以上环节的学习，学生充分地感悟数形结合思想，在积累“线动成面”的过程中，理解“求长方形的面积”就是求“几个几”的单位面积，并加以灵活运用。

很多时候，学生遇到新的问题时，都要利用知识间的联系将新的知识“转化”为已学的旧知识来尝试解决，在沟通、交流与整合中，实现数学知识的重构与融通。如，在“长方形的面积计算公式”的推导过程中，充分利用“数”与“形”相融的优势，以“形”直观表达数，以“数”对应阐述形，将抽象的问题变具体形象，这不仅有利于学生深层次地理解数学公式，更有利于学生全方位地积累相关数学活动经验。

（二）建构意义，培养空间观念

“图形与几何”领域的教学，要让学生充分经历由图形表征到算式表征的顺向思维过程，再由算式表征到图形表征的逆向转化过程，不断加深学生对意义的理解，培养学生的空间观念。几何图形中求长度、面积、体积的问题归根到底就是求“几个几”的问题，其数量关系式就是“每份数×份数=总数”。根据平移累加的原理，在操作“线动成面”的过程中，线的叠加就成了面，对面进行压缩就成了一条线，学生感受了客观事物之间的变化情况，理解了辩证统一的思想。

学生经历“观察感知”“图示表征”等过程后，获得从图形到算式的“抽象化”经验，并形成从计算逆推到图形的意义建构。今后在面对求某个图形的面积时，学生的脑海中首先呈现的是几条有宽度的“线段”平铺而成的面，完成由一维长度到二维平面的动态演变，透过面积公式的表达形式，发展空间观念。最终，学生不仅能灵活地运用具体的面积公式解决实际问题，还能真正地领会面积公式背后所蕴含的数学思想。

总之，基于几何直观的数学教学，教师要抓住数学知识的本质，帮助学生搭建探究性学习的平台，启发学生进行数学思考，让学生在掌握相关基础知识和基本技能的基础上，利用数形结合思想，积累实践活动经验。教学过程中，教师借助多种形式的学习方法，引领学生经历数学知识的形成过程，促进学生数学思维的发展，让学生的核心素养自然生长。

参考文献：

［１］ 杨慧娟． 数学实验在小学数学教学中的育人价值——以“长方形、正方形的面积计算”教学为例［Ｊ］． 小学数学教师，２０２１（０９）：７２－７５．

［２］ 王芳． 走向思维通透的深度阅读——“梯形面积公式联想”教学实践与思考［Ｊ］． 小学教学参考，２０２１（１２）：１４－１６．