在探究中培养学生几何直观能力——以“全等三角形”教学为例

江苏省常熟市外国语初级中学 濮 维

几何直观能力主要是指通过图形来描述问题并进行分析的能力，即通过图形将复杂的、晦涩的数学问题简化为具象的、清晰的几何问题，从而促进对问题解决思路的探索，实现对结果的预估.对学生几何直观能力的培养，不仅可以帮助学生对数学知识有更加直观的理解，更有利于提高学生的创新意识，培养学生的发散性思维，这在整个数学教与学过程中都非常重要.

全等三角形的研究本质是平面几何问题中对两个封闭的图形关系研究的第一步，它是两个三角形之间最简单、最直观的关系.它不仅是后面平面几何知识的基础，更是表示线段相等、角度相等这两种数量关系的重要理论依据.因此，教师在这一章节的教学中必须要求学生熟练掌握全等三角形的判定定理，并能灵活应用，以解决平面几何中相关的三角形问题.

1 培养学生几何直观能力的思路

正如我国著名数学家华罗庚所说“形缺数时难入微，数缺形时少直观”，几何直观正是揭示现代数学本质的重要工具.要想培养和发展学生的几何直观能力，必须结合实际的数学教材内容，以本班具体学情为依据，灵活编排课程设计和教学内容，并落实在课堂实践和教学细节中.

(1)重视概念、定理，夯实几何基础

几何概念是几何学的基础，在几何的概念教学中，仅讲授概念的意义，再要求学生记忆定理公式是远远不够的.教师应该从公式的本质和内在联系出发，对概念进行全面分析，这样才能帮助学生切实理解概念本质和内涵.几何学的特点是概念多、易混淆，概念教学极大地影响学生对几何学的学习能否入门.因此，在实际教学活动中，教师必须讲授定理内在的联系以及本质，让学生能真正地理解概念、分析概念、应用概念.

(2)多媒体辅助教学，丰富学生体验

自新课程标准实施以来，教师要改变教学观念，丰富课堂教学形式，以充实学生的课堂体验.教师要注重以学生综合素质的培养为教学目标，表现在具体的教学实践中，就是不断提高学生的思维能力，激发学生的自主能动性，让学生成为课堂主体，主动开展学习活动.多媒体教学是指在课堂上运用先进的多媒体技术，将影像、图片、声音结合，这种辅助模式不仅可以充分吸引学生的注意力，生动表现课堂内容，更能打破传统教学以老师为主体这种单一的教学模式，让学生的课堂体验更丰富.在多媒体辅助下，开展几何教学活动能够充分调动学生积极性，激发学生想象力和创造力，从而切实达到提高学生的几何直观能力这一教学目标.

(3)培养数感能力，让学生学会数形结合

数感能力是指学生对数字的敏感和接受能力，它也是新课程标准提出的有关核心素养的十大概念之一.培养学生的数感能力，不仅可以提高学生对数据的敏感度，更能锻炼学生对图形的观察力，提高学生的看图能力.在数学学习的过程中很多问题都可以通过图形加以解决，数形结合思想的使用场合不只局限于函数与方程，在几何问题上也有很大的应用空间.例如，通过数据寻找等量关系、倍数关系等，以此来判断几何图形的性质、特点，以及图形之间全等或相似关系等.

2 培养学生几何直观能力的实践

在数学教学中，教师不仅要针对学生几何直观能力的培养来设计教学内容，还要设计合理的教学方案，通过在教学方法中融入对学生几何直观能力的培养来达到预期的教学目标.接下来，以“全等三角形”为例，简述如何在指导学生认识全等三角形以及证明三角形全等的过程中提高学生的几何直观能力，从而达到学生数学能力的提升.

教学目标：

(1)知识与技能目标：

1)能够通过图形给出的信息大致判断三角形全等及全等的类型，并学会用数学符号来表示两个三角形全等的条件；

2)知道全等三角形的相关概念，能够在两个三角形中找到相对应的顶点、边和角，培养证明三角形全等的能力；

3)经历探究三角形全等的过程，学会添加辅助线来为全等三角形的证明增加有效条件.

(2)过程与方法目标：

1)在学习三角形全等的过程中针对三角形的顶点、角、边培养一一对应的数学原则，养成严谨的解题习惯；

2)在证明三角形全等时，可以通过判定方法来倒推条件，并为证明创造条件，培养逆向思维.

(3)情感与技能目标：

1)在认识两个完全重合的三角形时，通过将三角形旋转、平移，理解体会这一过程中图形变换的思想，养成动态思维.

2)在创造条件证明三角形全等时训练创造思维，并感知几何图形的奥妙.

教学重难点：

教学重点：学会寻找证明全等三角形所需的对应元素，理解全等三角形的概念以及全等的性质并将其运用在实际解题过程中.

教学难点：能够正确辨认三角形全等条件中对应的角与边，并采用正确的判定来证明全等.

教学步骤：

(1)知识回顾，巩固基础

在全等三角形教学之前，教师要带领学生有针对性地复习三角形这个板块的知识，设计一些与三角形概念性质等相关的问题，考查学生对三角形的熟悉程度.

问题1关于三角形我们学习了哪些概念？

问题2三角形的内角有什么特征？关于三角形内角有什么定理以及推论？

问题3以往学过的概念是针对单个的三角形还是针对多个三角形？

设计意图：在这个环节中，通过对三角形相关概念的回顾帮助学生建立学习三角形全等的基础.在三角形这样的几何图形的教学过程中，教师要注重对概念知识的深化，通过加深对概念的理解来提高学生的几何直观能力，这样学生在见到几何图形时能够一眼挖掘其中隐藏的性质，从而提高解决问题的效率.

(2)创设情境，引出概念

在学生回顾了有关三角形的概念之后，教师可以通过多媒体播放两个一模一样的三角形(如图1)，然后将其中一个三角形以动画的形式旋转、平移、放大以及缩小，让学生在观察动画的过程中思考这两个三角形的区别.比如，当其中一个三角形缩小旋转之后，它们之间是否具有相同的几何性质？这个三角形的边与角发生了什么变化？从而引出形状相同、大小相等的两个三角形，并给出它们所有相等的条件.

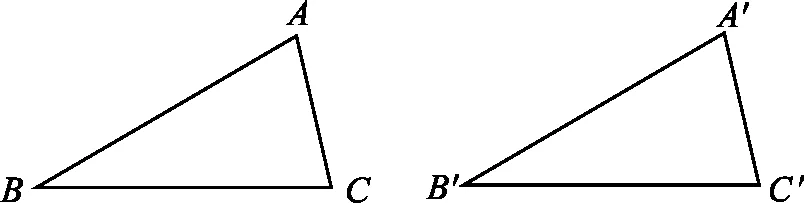
图1

设计意图：在这个环节中，借助多媒体等教学工具展示图形的变换，比传统的概念教学更能吸引学生的兴趣，且学生能够在动画的引导下，在脑海中针对图形的变换有一个直观的印象，有利于学生对图形性质的学习.最后让学生针对两个形状、大小都相同的三角形进行相等条件的挖掘，为学生后续学习三角形的判定奠定了基础.

(3)自主探究，总结规律

最后，教师要结合课本给出的数学符号让学生针对三角形全等的条件进行探索.已知两个三角形有三条对应边和三个对应角，那么满足几个条件就可以证明两个三角形全等呢？教师可以让学生以这个问题为切入点，寻找三角形的判定原理，并通过画图等方式来证明自己判断的正误.

设计意图：在这个环节中，教师选择让学生自主提出三角形全等的判定条件，然后通过画图等方式自主证明，提高学生的探究能力.教师还可以指导学生通过添加辅助线来完成三角形全等的证明，通过设想、推理、验证的过程训练学生解决几何问题的思维逻辑性，同时达到对学生几何直观能力的培养.

总的来说，几何直观能力就是指将复杂的数学问题用简单的图形表示出来，并能通过对图形的分析解决问题.培养学生的几何直观能力可以增强学生的逻辑思维能力、图形分析能力，更能激发学生的创新思维和探索精神，为后续长期的数学学习打下基础.上文针对初中数学教学过程中培养学生几何直观能力的几条思路，希望能给教育工作者带来一点启示.