基于改进长期增量成本法的可靠性电价制定方法
2023-03-23王子轩范须露
李 鹏,项 特,王子轩,范须露,王 楠,文 淼
(1.华北电力大学电气与电子工程学院,河北省 保定市 071003;2.国网天津市电力公司,天津市 300010)
0 引言
随着售电市场改革的深入,用户对供电可靠性拥有了自主选择的权利,其有权向供电公司提出更高的要求,以此保障用电的安全可靠;而供电公司的任务则是在优化营商环境的导向下满足不同区域、不同类型用户的差异化可靠性需求。电价作为电力价值的体现,能够有效反映电力在生产到消费过程中的价值波动[1-3],用户在可靠性需求上的差异必然导致电价的差异,这就要求供电公司能按差异化可靠性电价匹配不同等级的供电可靠性。
在开放的电力市场环境下,制定可靠性电价需综合考虑供应侧的可靠性成本和需求侧的供电可靠性。为降低可靠性成本,供电公司需充分发挥可中断负荷的用电灵活性,使其在系统紧急情况下能灵活中断[4-7],因此,考虑可中断响应的可靠性电价能更有效协调配电网规划中的可靠性与经济性。如何以最优的可靠性成本保障供电可靠性,并实现对用户可靠性服务的“按质论价、高质高价”是当前供电公司亟须解决的问题[8-9]。
差异化可靠性需求对可靠性电价的制定具有重要影响。为此,国内外学者对可靠性电价的制定展开了一系列研究。文献[10]根据用户可靠性需求,利用模糊聚类方法将系统中的用户划分为几类虚拟用户,并按照其需求水平购买相应的可靠性服务备用,然后将费用分摊到各类虚拟用户得到可靠性电价。文献[11]利用可靠性指标表征用户可靠性需求,提出了基于层次分析法的可靠性电价计算方法,由此计算得到的可靠性电价受主观因素影响较大。文献[12]提出了基于熵权-层次分析法的可靠性电价制定方法,改进了单一评价方法的不足,但忽视了可靠性成本对可靠性电价制定的影响。文献[13]提出计及多阶段规划与差异化可靠性需求的配电网可靠性电价,但在计算可靠性指标时未考虑可中断负荷对其产生的影响。
目前,中低压配电网常采用多期规划,负荷增长等微小功率注入会对系统可靠性成本产生影响。为将可靠性成本合理分摊给终端用户,需采用长期增量成本法计算可靠性电价[14]。文献[15]基于长期增量成本法,提出了计及供电可靠性的配电网节点电价计算方法,但文中只考虑了系统正常运行情况,忽略了紧急情况下单位注入功率变化对投资年限的影响。文献[16]提出了基于组件可靠性的长期增量成本法,并采用该方法计算配电网多阶段规划中可靠性成本的变化,但其只考虑了组件的可靠性年限,并未考虑其经济年限。文献[17]提出了考虑可靠性和中断容忍度的可靠性电价计算方法,但终端用户的差异化需求未能在文中体现。综上,制定一套合理的可靠性电价定价体系需综合考虑用户的差异化可靠性需求、组件的经济投资年限和实际网络投资。
因此,本文提出了基于改进长期增量成本法的配电网可靠性电价制定方法。该方法结合经济投资策略分析了单位注入功率对经济投资年限的影响,并根据经济投资年限推导出可靠性成本增量,由此计算出不同供电分区的可靠性电价。最后,计及用户差异化需求,引入单位可靠性增量成本制定了增量电价的定价方法。算例分析表明,由区域可靠性电价和增量电价相结合的可靠性电价体系合理有效。
1 计及负荷中断与负荷转供的可靠性指标
负荷转供能在系统处于紧急情况下为更多终端用户提供更多供电可靠性[18-19],而可中断负荷可以为负荷转供提供额外的备用以提升可转供容量[20]。
为充分挖掘馈线的供电潜能和各类用户可中断响应的潜力,本文将配电网多类型终端用户分为可中断负荷和不可中断负荷,引入可中断响应因子表示各负荷点可中断负荷占比情况,并利用故障时可转供容量作为负荷转供时的馈线容量约束:
式中:Str为联络馈线可转供容量;Smax为联络馈线允许的最大配电变压器(本文简称配变)容量[18];α为线路容量裕度,取0.9;U为联络馈线电压;I为联络馈线允许通过的最大电流,根据联络馈线线型及截面积取值;ς为联络馈线上所有配变的最大负荷同时率,一般取为0.8;ρ为配变负载率;Sp为联络馈线已有配变容量之和;βL,u为负荷点u的可中断响应因子;DL,u为负荷点u的负荷量;Nfu为该联络馈线上的负荷点总数。
1.1 用户供电可靠性指标
配电网中存在大量工业、商业和居民等多类型终端用户,并且其用能特性和可靠性需求存在较大的差异性。首先,结合配电物联网建设成果和配电自动化系统获取多类型终端用户的多元化用能和供电可靠性信息,对停电信息进行时空多维度分析。然后,根据文献[21]所提的故障节点划分方法对故障所在馈线上的所有节点进行分类,节点分类结果如表1 所示。接着,根据文献[18]所提的负荷转供策略对馈线上所有节点进行负荷转供和容量约束校验。最后,结合可中断响应因子建立平均停电频率(频率型)、平均停电时间(时间型)、供电可靠率(时间型)和期望缺供电量(电量型)等负荷点多类型供电可靠性指标。
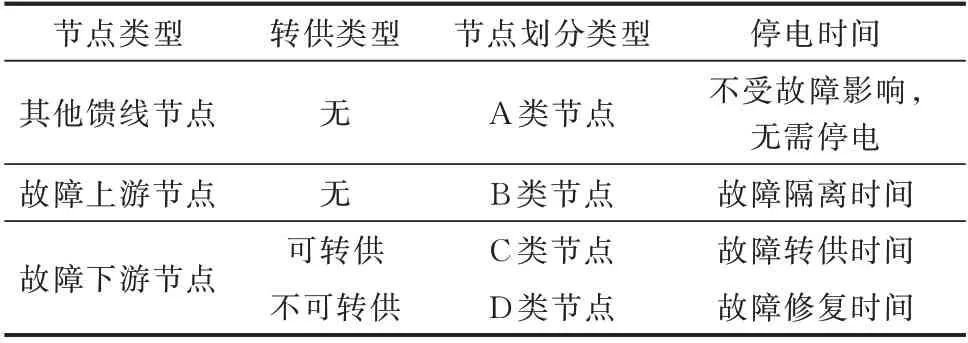
表1 节点类型划分Table 1 Node type division
1)负荷点平均停电频率λL,u
式中:λe为负荷点等效故障率[18];NB、NC、ND分别为被划为B、C、D 类节点的故障次数;Ne为故障总次数。
2)负荷点平均停电时间tL,u
式中:tB为故障隔离时间;tC为故障转供时间;tD为故障修复时间。
3)负荷点供电可靠率AL,u
4)负荷点期望缺供电量QEENS,L,u
1.2 供电分区可靠性指标
对于得到的计及负荷中断与负荷转供的负荷点可靠性指标,将负荷点供电可靠率大于等于99.990%的划入Ⅰ类供电分区,将负荷点供电可靠率大于等于99.965%、小于99.990%的划入Ⅱ类供电分区,将负荷点供电可靠率大于等于99.863%、小于99.965%的划入Ⅲ类供电分区。各类供电分区可靠性指标按下式计算:
式中:tq为第q类供电分区的平均停电时间;mq为第q类供电分区内总的负荷点数;NL,u为负荷点u的用户数;Nq为第q类供电分区的总用户数;λq为第q类供电分区的平均停电频率;QEENS,q为第q类供电分区的期望缺供电量;Aq为第q类供电分区的供电可靠率。
2 计及经济投资策略的可靠性成本模型
2.1 供电分区单位停电损失数学模型
在大多数的停电损失计算方法中,常把单位停电损失作为固定值,而实际上供电分区单位停电损失是随停电时间变化的量[22],其与终端用户类型、各类型终端用户用电量占比、各类型终端用户停电损失时间常数以及停电持续时间直接相关。计及以上影响因素,本文采用单位停电损失p随停电时间变化的指数型数学模型:
式中:pq为第q类供电分区的单位停电损失;τq为第q类供电分区的停电损失时间常数;kq为第q类供电分区内用户类型数量;δq,l为第q类供电分区内第l类终端用户的用电量比例;pq,l为第q类供电分区内第l类终端用户的单位停电损失参考值;τq,l为第q类供电分区内第l类终端用户的停电损失时间常数。pq,l和τq,l由 调 查 统 计 得 到,各 供 电 分 区 的 停 电损失时间常数取几何算术平均值。
2.2 考虑经济投资策略的供电分区可靠性成本
为更好地平衡配电网长期规划中的可靠性和经济性,兼顾电网公司和电力用户双方的利益,结合参考文献[15]对配电网元件经济寿命的定义(配电网经济投资年限,即配电网元件从使用到因经济不合理而停止使用所经历的时间,该年限区别于由元件质量、使用和维护情况所决定的元件物理年限,能更精确地评估停电损失情况),提出以下配电网经济投资策略。
1)在该经济投资年限内,配电网供电分区的可靠性成本不小于最大停电损失与需求响应成本之和。计及负荷增长率、可中断响应因子、供电分区最大停电时间和配电网经济投资年限等影响因素,各供电分区的最大停电损失数学模型如式(8)所示。
式 中:Cout,max为 最 大 停 电 损 失;tq,max为 第q类 供 电 分区最长停电时间;rq为第q类供电分区年负荷增长率;T为配电网的经济投资年限;Dq为第q类供电分区的总负荷量;βq为第q类供电分区的可中断响应因子。
计及可中断响应因子的需求响应成本CDR为:
式中:ccomp为可中断负荷的单位电能补偿成本;Dint为可中断负荷量。
考虑配电网经济投资策略的供电分区可靠性成本Creli为:
2)不同供电分区的供电可靠率应满足各供电分区的供电可靠率标准;计及需求响应后的各供电分区的平均停电时间不超过供电分区的停电时间最大值;可中断负荷量需小于最大可中断负荷量;在系统紧急情况下,支路潮流Pij不越限,负荷点电压VL,u保持在正常范围。若不满足以上约束条件之一也将触发可靠性增量成本。
式 中:Aq,max和Aq,min分 别 为 供 电 可 靠 率 上 限、下 限;Dint,max和Dint,min分 别 为 可 中 断 负 荷 量 上 限、下 限;Pij,max和Pij,min分 别 为 支 路 潮 流 上 限、下 限;VL,u,max和VL,u,min分别为负荷点电压上限、下限。
3 计及可靠性成本增量与差异化可靠性需求的配电网可靠性电价计算
3.1 基于改进长期增量成本法的区域可靠性电价计算
相比于原定价模型[15],本文提出的改进增量成本法将可靠性成本引入长期增量成本法中来研究正常运行和紧急情况下单位注入功率和可中断响应因子对配电网经济投资年限的影响。
为更好地区分系统正常运行和紧急情况2 种运行方式,本文基于各负荷点的紧急系数修正正常状态下的额定容量,得到紧急情况下的最大可用容量,依此来区分各负荷点应对系统紧急事件的能力。紧急系数定义为所有紧急事件中,流过各负荷点最大的潮流与正常情况下潮流的比值,较大的紧急系数表示负荷点上更多的额定容量需要作为备用容量预留给偶发的紧急事件,以承受紧急情况给系统带来的影响。
3.1.1 系统正常运行方式下的经济投资年限
在负荷点注入单位功率前的正常运行方式下,为满足用户的可靠性需求,系统在保证足够的备用容量下要满足所有的可中断负荷和不可中断负荷的正常供电。此时,系统最大可用容量为:
式中:Dmax,ava为系统最大可用负荷容量;Tnor为在正常运行方式下负荷点注入单位功率前的经济投资年限;Drated为负荷额定容量;ψCF为紧急系数;Duni为正常运行方式下的不可中断负荷量。
由式(12)可得系统在正常运行方式下负荷点注入单位功率前的经济投资年限Tnor为:
在负荷点注入单位功率后的正常运行方式下,考虑负荷点注入单位功率产生的增量潮流对经济投资年限的影响。此时,系统的最大可用容量满足下式:
式中:Tnor,new为正常运行方式下负荷点注入单位功率后的现经济投资年限;ΔPnor为正常运行方式下负荷点注入单位功率引起的增量潮流。
由式(14)可得系统在正常运行方式下负荷点注入单位功率后的现经济投资年限Tnor,new为:
3.1.2 系统紧急情况下的经济投资年限
在负荷点注入单位功率前的紧急情况下,各负荷点需要保证所有不可中断负荷的供电需求,部分线路流过的最大潮流包括故障线路在其正常运行方式下保障的不可中断负荷以及本线路在紧急情况下潜在的不可中断负荷。在此类紧急情况下,系统的经济投资年限Tcon为:
式中:Duni,con为紧急情况下的不可中断负荷量。
在负荷点注入单位功率后的紧急情况下,考虑到负荷点注入单位功率产生的增量潮流对配电网经济投资年限的影响,计算得到现经济投资年限Tcon,new为:
式中:ΔPcon为紧急情况下负荷点注入单位功率引起的增量潮流。
每当系统中负荷点有单位功率注入时,配电网即需进行1 次潮流计算,对于大型系统在正常运行方式和紧急情况下,计算负荷点注入单位功率产生的增量潮流非常耗时。由于负荷点注入单位功率相较于整个系统潮流来说是个极小值,因此,采用灵敏度分析法得到的增量潮流结果与潮流仿真结果相似,具有较高计算精度,且该方法适用于正常运行方式和紧急情况。本文采用计算量较小的支路灵敏度分析法计算增量潮流:
式中:ΔPij为负荷点注入单位功率产生的增量潮流;VL,i为 负 荷 点i的 电 压 值;Din为 负 荷 点 的 单 位 注 入功 率;VL,j为 负 荷 点j的 电 压 值;θL,i为 负 荷 点i的 相角值;θL,j为负荷点j的相角值。
3.1.3 不同运行方式下的区域可靠性电价计算
根据系统2 种运行方式下较小的经济投资年限推导得到原经济投资年限和现经济投资年限下的可靠性成本Creli、Creli,new分别如式(19)和式(20)所示。
区域可靠性电价ρ0,即为供电分区可靠性成本增量ΔCreli与负荷点单位注入功率之比:
3.2 考虑差异化可靠性需求的增量电价计算
当前中国各地供电可靠性保持在较高水平。减少用户停电时间、提升供电可靠性以满足用户可靠性需求始终是电网公司供电环节的重中之重。因未满足经济投资策略和用户可靠性需求而触发的可靠性增量成本将直接反映在供电分区中各类用户的电价中,所以采用单位可靠性增量成本计算可靠性增量电价,以同时反映可靠性增量成本、供电可靠性和用户可靠性需求的变化对电价制定的影响。
可靠性增量成本包括升级改造成本和运行维护成本。升级改造成本CUR由新建配电网线路、新建分布式电源、新建变电站、变电站扩容和应急资源配置等成本组成。
式 中:CL,y为 线 路y单 位 长 度 的 铺 设 费 用;Ly为 线 路y的长度;NL为配电网线路总数;CDR,o为第o种分布式电源的投资费用;NDR为分布式电源种类个数;CSS,g为 新 建 变 电 站g的 投 资 费 用;Ng为 新 建 变 电 站总数;CKSS,f为扩容变电站f的投资费用;Nf为扩容变电 站 总 数;Nv为 移 动 储 能 应 急 车 数 量;Cms,v为 移 动储能应急车v的投资费用;μ为贴现率。
运行维护成本COM由配电网线路运行维护成本、各电压等级变电站运行维护成本以及网损成本组成。
式中:CDROM,o为第o种分布式电源运行维护费用;H为配电网电压等级分布集合;NSS,h为第h个电压等级的变电站数量;CTOM,h为第h个电压等级变电站运行维护总成本;CLOM,h为配电网线路单位长度的检修成本;WS为配电网年网损功率;tDN为配电网年运行时间。
供电分区内增加单位供电可靠率所产生的单位可靠性增量成本Cinc为:
式中:ΔA为供电分区内供电可靠率变化量。
根据单位可靠性增量成本得到的可靠性增量电价ρz为:
式中:Auser,q为第q类供电分区终端用户的期望供电可靠率。
3.3 配电网终端用户可靠性电价
本文得到的配电网终端用户可靠性电价ρuser由区域电价ρ0和增量电价ρz组成,具体表示为:
式 中:ζ为 供 电 可 靠 性 系 数,0.999 <ζ<0.999 9;ρ0,min为所设可靠性电价最低值,取值为0.2元/(kW·h)。
配电网终端用户可靠性电价具体制定流程如图1 所示。
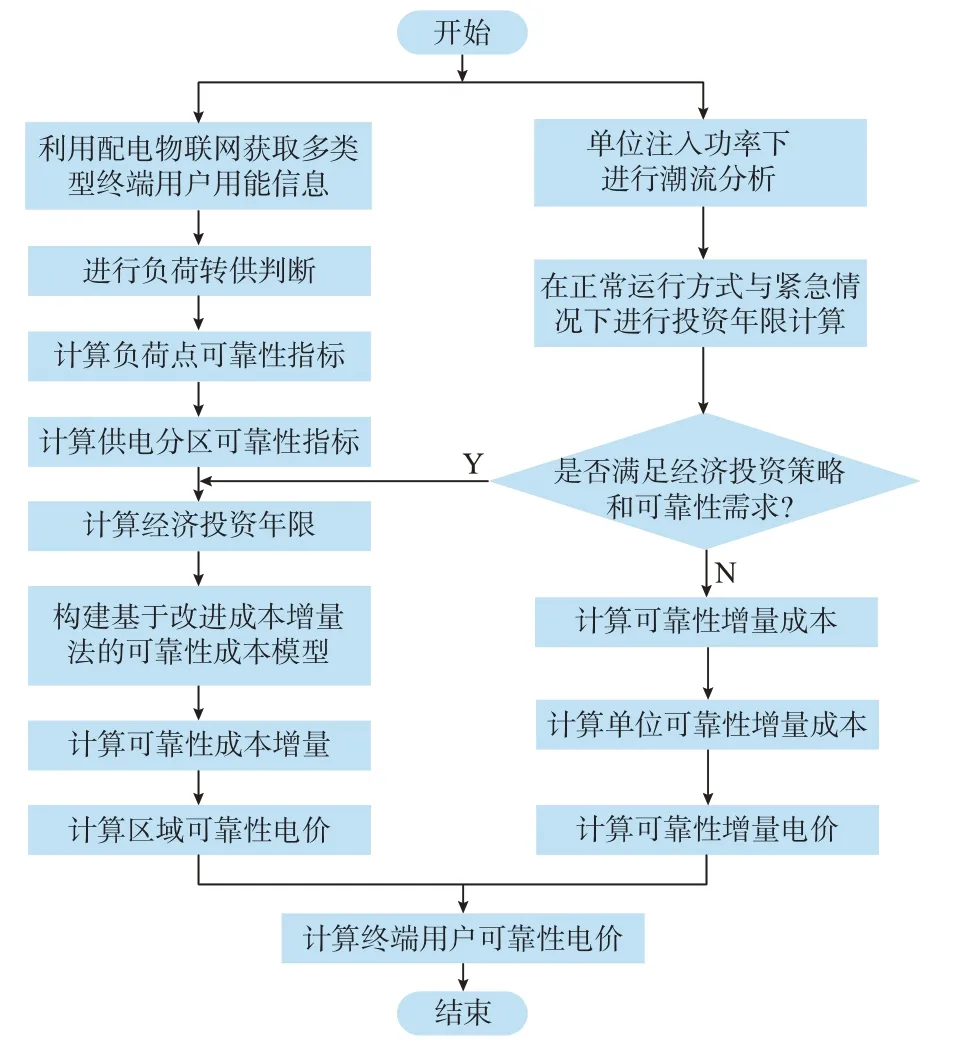
图1 配电网终端用户可靠性电价制定流程图Fig.1 Flow chart for reliability pricing of end users in distribution network
4 算例分析
本文采用中国天津某示范园区所在区域的部分用户供电可靠性数据进行算例分析,各园区所在区域含有数量合适的农业、居民、工业、商业和市政等多类型终端用户,各类型终端用户分布集中且可靠性需求差异明显,能较好地符合本文划分供电分区的需要。部分供电区域网架结构见附录A 图A1 和图A2,负荷参数见附录A 表A1 和表A2。利用多类型用户的用能信息和实际响应情况,建立计及负荷中断和负荷转供的频率型、时间型和电量型等供电分区供电可靠性指标,各供电分区的可靠性指标如表2 所示。
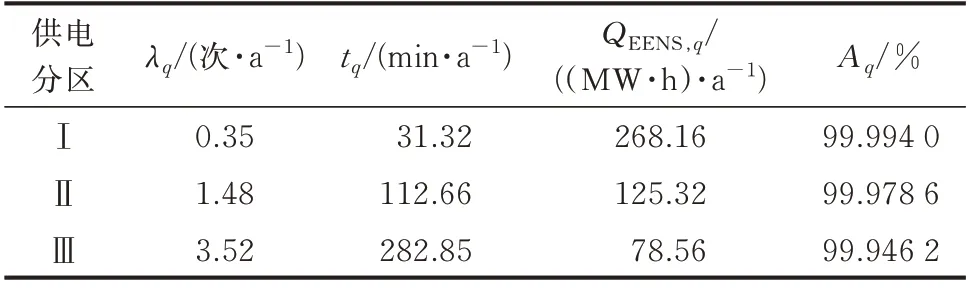
表2 供电分区可靠性指标Table 2 Reliability indices of power supply zones
在计及负荷中断和负荷转供后,频率型可靠性指标数值保持不变;时间型可靠性指标平均停电时间较响应前分别下降1.8%、3.1%和4.6%,供电可靠率较响应前也有所改善;电量型可靠性指标期望缺供电量较响应前分别下降2.9%、3.8%和5.6%。由可靠性评估结果可见,负荷中断和负荷转供的实施能提高供电分区的供电可靠性。
依托示范园区所在区域的实际调研统计,得到的3 类供电分区内各类用户单位停电损失参考值如表3 所示,各类用户用电比例情况如表4 所示。

表3 供电分区内各类用户单位停电损失参考值Table 3 Reference values of unit outage cost of various users in power supply zones
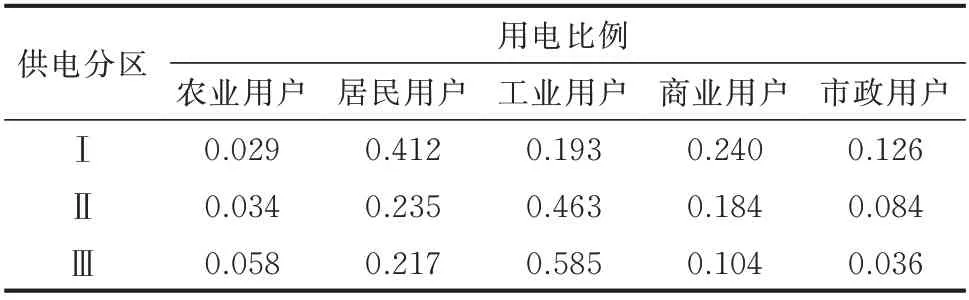
表4 各类用户用电比例Table 4 Electricity consumption ratio of various users
4.1 配电网不同运行方式下的经济投资年限
经统计,配电网Ⅰ类供电分区年负荷增长率为1.8%,Ⅱ类供电分区年负荷增长率为2.2%,Ⅲ类供电分区年负荷增长率为2.8%。假设可中断负荷单位电量补偿价格为2 元/(kW·h),结合3.1 节所提方法得到系统正常运行和紧急情况下考虑单位注入功率和可中断响应因子前后经济投资年限对比结果,如图2 所示。由图2 可知,在有单位注入功率的情况下,系统正常运行状态下各供电分区经济投资年限分别下降6.53%、4.74%、6.50%,紧急情况下各供电分区经济投资年限分别下降6.52%、4.49%、5.83%,紧急情况下的下降幅度略小于正常运行方式,因为无论在正常运行方式下还是紧急情况下,单位注入功率产生的增量潮流都会改变系统整体的潮流分布,各供电分区在正常运行方式和紧急情况下的经济投资年限会因为产生的增量潮流而降低。
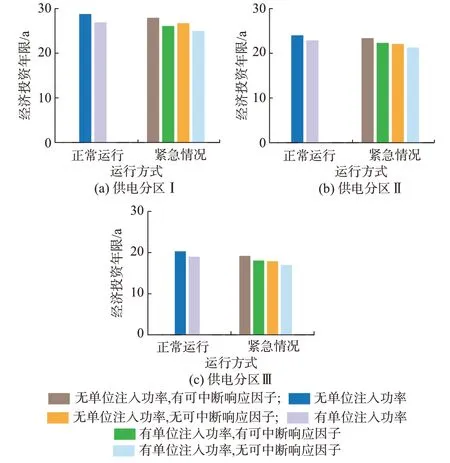
图2 经济投资年限计算结果Fig.2 Calculation results of economic investment horizon
对比正常运行方式和紧急情况下注入单位功率前的情况,紧急情况下各供电分区的经济投资年限均低于正常运行方式。其原因在于:紧急情况下,系统部分线路需要承担本线路不可中断负荷及故障线路上的不可中断负荷,即紧急情况相较于正常运行方式需考虑紧急系数的影响,流过该线路的最大紧急潮流大于正常运行时的潮流,按式(16)计算紧急情况下的经济投资年限会降低。
由于可中断响应因子不影响系统正常运行时的经济投资年限,此处只分析紧急情况下可中断响应因子对经济投资年限的影响。在注入单位功率前,考虑可中断响应因子后各供电分区经济投资年限相较于原模型分别上升4.53%、5.93%、7.15%;在有单位注入功率的情况下,考虑可中断响应因子后各供电分区的经济投资年限分别上升4.48%、4.88%、6.28%。由此可见,考虑可中断负荷可以提高经济投资年限,有效延缓配电网进行升级改造。
4.2 各类供电分区可靠性成本与区域可靠性电价
基于4.1 节得到的配电网在不同运行方式下的经济投资年限,取本文所设4 种情况下最小的经济投资年限通过改进长期增量成本模型得到可靠性成本增量及区域可靠性电价如表5 所示,本文模型与原模型[15]分析的数据对比如表6 所示。
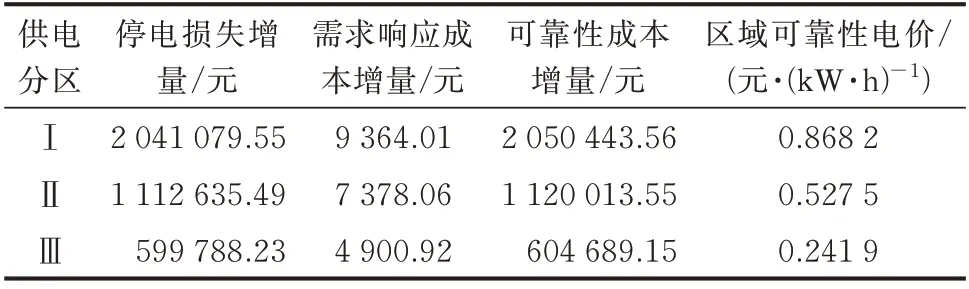
表5 供电分区可靠性电价和可靠性增量成本计算结果Table 5 Calculation results of reliability price and incremental reliability costs of power supply zones

表6 不同模型的计算结果对比Table 6 Comparison of calculation results with different models
由表5 可知,不同供电分区的区域可靠性电价有着较大差异,Ⅰ类供电分区区域可靠性电价最高,Ⅱ类供电分区次之,Ⅲ类供电分区最低。在可靠性成本增量中停电损失增量占绝大部分比例,需求响应成本增量微乎其微。其原因在于:单位停电损失参考值远大于可中断负荷单位补偿成本,故需求响应成本对于区域可靠性电价的影响很小。由表5 和表6 可知,所提模型基于改进长期成本增量法并计及需求响应后,可靠性成本增量低于原模型,并且分别降低10%、15.02%、20.01%,区域可靠性电价分别降低9.61%、14.48%、19.12%。虽然考虑紧急情况使得经济投资年限降低,但是计及可中断响应因子后,可中断负荷的用电灵活性使得供电分区的停电损失增量和区域可靠性电价降低,相比原模型展现了更好的经济性。在结合系统运行方式和可中断响应因子后的区域可靠性电价相比于原模型更符合实际情况,并且符合“高质高价”的定价原则。
图3 比较了5 种可中断响应因子场景下的停电损失增量、可靠性成本增量和区域可靠性电价情况。所设置场景为:场景1 中可中断影响因子为0%(原模型);场景2 中可中断影响因子为5%;场景3中可中断影响因子为10%;场景4 中可中断影响因子为20%;场景5 中可中断影响因子为30%。由图3 可知,同一供电分区的停电损失增量、可靠性成本增量和区域可靠性电价都随着可中断响应因子的增大而减小,需求响应成本小幅增大。在场景1 中,原模型不考虑负荷中断和系统紧急情况,所有终端负荷都需保证正常供电,故停电损失增量和区域可靠性电价为所有场景中的最大值。在场景5 中可中断响应因子达到30% 时,Ⅲ类供电分区可靠性电价为0.212 9 元/(kW·h),接近设定的最低电价0.2 元/(kW·h)。5 类场景所示的区域可靠性电价结果证明了本文所提方法合理有效。
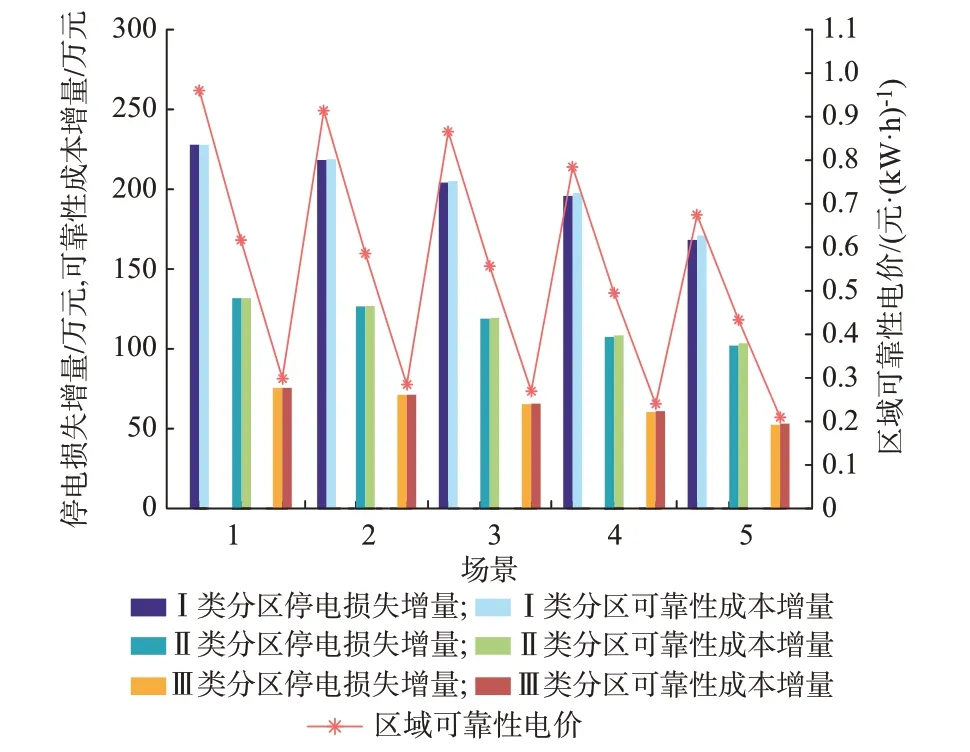
图3 不同场景下的供电分区可靠性电价Fig.3 Reliability price of power supply zones in different scenarios
4.3 考虑差异化需求的终端用户可靠性电价
各供电分区未满足经济投资策略或未能满足分区内用户可靠性需求会产生新的可靠性成本,供电分区Ⅰ、Ⅱ、Ⅲ因提升单位供电可靠率所产生的可靠性增量成本分别为1 050.82、703.53、481.39 万元。由此可知,供电可靠率所对应的单位可靠性增量成本在不同供电分区内存在较大差异。供电可靠性较高的Ⅰ类供电分区因提升单位供电可靠率所产生的投资费用明显高于其他2 类供电分区。
考虑到配电网中的终端用户种类繁多,各终端用户对供电可靠性需求存在差异,图4 给出了考虑用户差异化需求的可靠性电价。
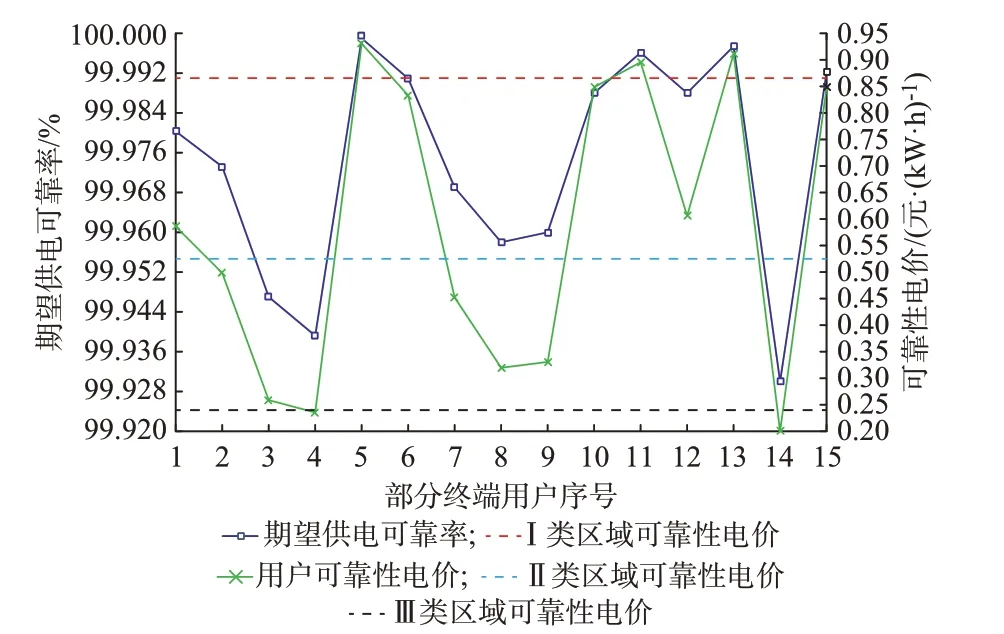
图4 考虑用户差异化需求的可靠性电价Fig.4 Reliability price considering differentiated demands of users
由图4 可知,终端用户可靠性电价与期望供电可靠率的变化趋势一致,差异化的可靠性需求服务产生了差异化的可靠性电价。相比于各供电分区可靠性电价的无差别定价方法,差异化可靠性电价能有效反映可靠性增量成本,有利于各供电分区投资成本的有效回收。因此,结合不同供电分区的供电可靠性水平,为用户提供差异化的可靠性电价来匹配其可靠性需求,能同时兼顾电网公司的利益和用户电价的公平性。
5 结语
本文提出基于改进长期增量成本法的配电网可靠性电价定价方法,能正确地反映供电分区的供电可靠性水平和可中断负荷响应情况,并能匹配不同的终端用户的可靠性需求。在引导用户灵活合理利用电能资源的同时,可为电网公司进行配电网差异化规划及制定差异化的可靠性电价提供参考。通过算例分析得到以下结论:
1)将负荷中断和负荷转供相结合能充分挖掘馈线的供电潜力,提升供电可靠性。本文提出的改进长期增量成本模型综合考虑了系统运行方式和可中断响应因子,优化了配电网经济投资年限和可靠性成本,在不同可中断因子场景下得到的区域可靠性电价结果验证了此方法的有效性与合理性。同时,表明所提模型改善了原模型只计及正常运行情况的不足。
2)本文提出将区域可靠性电价和可靠性增量电价相结合使得可靠性电价定价体系更加完整,不仅能反映供电分区的供电可靠性和用户的整体响应情况,也能体现不同终端用户差异化的可靠性需求,可有效平衡配电网规划中的可靠性和经济性,具有良好的推广前景。
此外,本文研究仍存在一些不足。在新型电力系统构建过程中用户的用能灵活性和不确定性进一步增强,文中暂未考虑需求不确定性对可靠性电价的影响,将在后续研究工作中有所体现。
附录见本刊网络版(http://www.aeps-info.com/aeps/ch/index.aspx),扫英文摘要后二维码可以阅读网络全文。
