考虑燃料电池汽车加氢负荷的电-氢系统协同优化运行
2023-03-23袁铁江田雪沁李国锋
袁铁江,计 力,田雪沁,李国锋
(1.大连理工大学电气工程学院,辽宁省 大连市 116024;2.国网经济技术研究院有限公司,北京市 102209)
0 引言
氢能作为一种优质的二次能源,在能源转型与零碳出行上表现出巨大潜力[1]。燃料电池汽车(hydrogen fuel cell vehicle,HFCV)作为绿色交通工具受到广泛关注,国家发改委、国家能源局联合印发氢能产业发展中长期规划[2],预计到2025 年HFCV保有量约为5 万辆。随着技术发展成熟和制氢成本下降,HFCV 以其能量密度高、零排放、加注速度快等特点,具有广阔的发展前景[3]。因此开展配电网和交通网以及氢能系统(hydrogen energy system,HES)协同优化具有重大研究意义。
针对配电网与交通网耦合研究,文献[4]提出电力-交通融合,并指出两者耦合主要体现在规划与运行层面。文献[5]以捕获交通流量最大、配电网损耗及节点电压偏移最小为目标,建立了充电站规划模型。但是没有考虑系统不确定性以及交通网络(transportation network,TN)均衡问题,新能源出力的不确定性研究方法可以分为随机优化、鲁棒优化和分布鲁棒优化。文献[6]考虑新能源、负荷及交通需求不确定性,提出两阶段鲁棒优化模型,有效降低了耦合系统运行成本。文献[7]建立了由日前调度阶段和实时调整阶段组成的两阶段鲁棒优化模型。文献[8]利用蒙特卡洛模拟生成多种随机场景应对新能源出力与负荷不确定性。文献[9]提出基于用户均衡的多时间尺度时空网络两阶段随机模型,通过提高配电网灵活性来降低系统预期运营成本。文献[10-11]采用数据驱动处理源、荷及交通流量的不确定性,需要指出的是,耦合节点负荷不单纯是将经过该节点的交通流量与充电率系数乘积,因此所得到的叠加负荷表征更加困难[12]。
针对电力与氢能系统耦合研究,大多数研究聚集于加氢站选址定容。文献[13]建立了考虑交通流量捕获的加氢站、风电场与电网的联合规划模型。文献[14]对氢气运输成本进行精细化建模。可再生能源制氢与电力结合使零碳出行成为可能。文献[15]针对HFCV 将来广泛部署的情况,建立私有加氢站优化调度模型,为电力市场运营商提供辅助服务。文献[16]论证了在风力发电渗透率高的地区利用弃风制氢为HFCV 提供燃料的技术经济可行性。文献[17]以投资成本最小为目标函数满足HFCV负荷,建立加氢站、可再生能源及电解槽容量规划模型。但这些电力-氢能系统耦合研究很少结合交通网络。
综上所述,本文提出考虑HFCV 加氢负荷的电-氢协同优化运行模型。首先,基于用户出行需求,采用Dijkstra 算法规划加氢路径,得到计及加氢行为下交通流量分配模型与配电网负荷模型。其次,针对新能源出力不确定性问题,利用预测误差样本数据,构建基于Wasserstein 距离模糊集,运用强对偶理论将复杂的分布鲁棒优化模型转化为混合整数线性规划问题。最后,算例以IEEE 33 节点配电网与24 节点交通系统组成的耦合系统验证了所提模型和求解方法的有效性。
1 电-氢-交通耦合系统与HFCV 加氢负荷建模
1.1 模型构建
电-氢-交通耦合系统包括配电网、氢能系统和交通网络。HFCV 作为配电网、氢能系统、交通网耦合元件,在加氢站进行加氢,实现电-氢-交通耦合互动。电-氢-交通耦合系统结构如图1 所示。

图1 电-氢-交通耦合系统Fig.1 Coupled electricity-hydrogen-transporation system
1.1.1 氢能系统
氢能系统中,加氢站通过电解槽装置消耗上级电网与风电场的电力来生产氢气,加压存储。当HFCV 加氢时,通过加氢机将储氢罐中的高压气态氢充入HFCV,由于加氢时间相较于行驶时间来说很短,在本文中不考虑加氢站等待以及充注时间。不考虑加氢过程中产生的能量损耗,建立如下制氢模型[18]:
式中:ηe为电解槽产氢效率;PH为电解槽消耗电功率;HHV为氢气的高热值(3.509(kW·h)/(N·m3));vh为电解槽产氢速率。
电解槽的实际运行模型可以近似为线性关系,此时的电解槽输入、输出特性如(2)所示。
加氢站中采用储氢罐来存储多余的氢气进行备用,储氢模型如式(3)所示。
1.1.2 交通网络模型
交通网络模型可以看作是由一系列道路和路口组成的无向图G={TN,TL},其中TN为节点集,TL为线路集。其中,节点N对应交叉路口,线路L对应连接节点的道路,道路拓扑结构采用道路邻接矩阵进行描述。对于一个由N个节点、M条支路组成的交通网络,可以进一步表示为邻接矩阵A,其表达式为:
式中:如果第m条支路是从i节点到j节点,则Amj=1;否则,Amj=-1,其余分量为0。行向量对应支路,列向量对应节点。
1.1.3 配电网模型
同区域交通网相连的配电系统,配电网为辐射状网络,本文采用文献[20]方法对配电网潮流进行建模,其潮流方程形式如下:
1.1.4 电-氢-交通网络耦合关系
交通网络和电-氢网络通过加氢站进行耦合。对于HFCV 而言,每辆车出行时间和目的地不同导致道路阻抗的变化,道路阻抗时空特征影响加氢路径的选择,反映在配电网与氢能系统上,氢负荷的时空分布进一步影响配电网功率分配以及加氢站新能源并网与就地消纳比例。
式 中:Pj,t为 节 点j在t时 刻 的 有 功 负 载;Pj,0为 原 始负载。
1.2 HFCV 加氢负荷
HFCV 行驶里程和氢气状态(state of hydrogen,SOH)决定了HFCV 加氢时刻与加氢量。当行程结束或开始时,车主根据此时SOH 和未来行驶里程来判断是否加氢:当HFCV 的SOH 超过当前目的地行驶需求则继续行驶,直到该段行程结束;当SOH 低于阈值或者不能满足当前行程时则就近加氢,当加氢量满足当前目的地里程需求则停止加氢。
HFCV 出行需求采用交通起止点(originaldestination,OD)矩阵来刻画,(r,s)定义为OD 对,其中,r为OD 对 起 点,s为OD 对 终 点,W为OD 对 矩阵。出发节点和到达节点通常为工作区或住宅区,途经节点通常为路口等。
式中:Wmn为从节点m出发去节点n的车流量。
1.2.1 HFCV 路径优化模型
本文所提出的考虑HFCV 加氢参与综合能源系统优化运行,主要是针对出行需求随机且行驶路径不固定的私家车,行驶时间和路线固定的公交车不在讨论范围。因此,建立HFCV 加氢特性和行驶特性模型[21]:
式中:CR为加氢特性参数集合;Ch、ts、td、Ht、Hc、HF分别为加氢站编号、加氢开始时间、加氢结束时间、t时刻的SOH、每公里耗氢量和加满时的SOH;TR为行驶特性参数集合;Nv、Lt、Rp、Oep、Des分别为车辆编号、t时刻车辆位置、行驶路径、车辆出发点和车辆目的地。
1)道路阻抗函数
在建立的交通网络的基础上,本文主要考虑用户的出行需求,交通时间作为出行者在进行路径选择时的首要考虑,道路阻抗函数是反映路段行驶时间与路段交通负荷等因素之间的关系。因此,将行程时间与出行成本作为道路阻抗进行分析。常用的路阻函数采用美国联邦公路局(Bureau of Public Roads,BPR)函数计算[22],即
2)位置初始信息
系统对HFCV 进行统一标号,通过随机生成OD 对确定出发点与车辆目的地,通过改进后的Dijkstra 算法得到HFCV 在加氢约束下的最优行驶路线。
3)加氢状态判断
假设HFCV 剩余里程小于出行里程,保证每辆HFCV 至少经过一次加氢站,并且假设HFCV 有足够的燃料行驶到加氢站完成加氢。当Ht满足式(19)时,车辆做出加氢行为并找到此时距离最短的加氢站。
式中:d(i,t)为第i辆车t时刻的位置与目的地之间的距离;H(d(i,t))表示完成d(i,t)距离所需要的SOH。
4)基于Dijkstra 算法规划加氢路径
以Dijkstra 算法为基础,融入实时路况信息,为用户动态规划耗时最短的出行路径,即用户车辆每出行至一个节点,该算法能够自动根据路况变化,调整前期规划路径,确定下一目标节点。具体步骤如下[23]。
步骤1:根据交通网络邻接矩阵、路阻函数、OD对获取实时路阻函数与起讫节点。对路网中所有节点分成2 个集合S和W,分别记录已求出最小路阻节点和尚未求出最小路阻的节点。
步 骤2:初 始 化。S中 只 包 含 起 点v0且d(v0,v0)=0,W中 包 含 除v0之 外 的 节 点,且W中 节 点 距离起点路阻值(v0,vi)=G(v0,vi),其中G(v0,vi)表示所有道路的路阻。
步骤3:按式(20)计算W中节点到起点最小路阻值,并记录替换信息p(i)=k。
步骤4:从W中选取路阻值最小的节点vk,将节点vk加入集合S,同时将其从W中移出。
步骤5:重复步骤3 和步骤4,直至遍历所有节点,利用回溯法从p中读取现阶段行驶至目标节点的最优路径。
步骤6:根据步骤5 中所求路径行驶至下一节点,并记录实时最优路径。更新v0转向步骤1,直至目标节点。
1.2.2 加氢负荷计算方法
对具有加氢约束下的车辆出行路径进行规划,流程图如附录A 图A1 所示,整个加氢路径规划流程如下。
首先,获取交通网信息包括路段长度、路段最大交通流量和路段阻抗,读取交通网中HFCV 出行信息,包括出行时间、初始位置、车辆目的地和车辆SOH。
根据车辆当前位置信息得到剩余里程信息,通过加氢状态判断是否需要进行加氢。若需要,则为车辆搜索剩余SOH 范围内最近的加氢站,采用Dijkstra 算法规划加氢路径,用户根据车辆剩余氢气量、当前位置与该车辆目的地距离进行加氢,得到此时加氢站的氢气负荷;若不需要,则按规划路径行驶。对系统内所有车辆到达目的地情况进行判断,当所有车辆路径规划完成则退出。节点j在t时刻的加氢站负荷为:
式中:Hi,t为第i辆HFCV 在t时刻的SOH;δ(·)表示HFCV 路径优化函数,得到加氢需求与所选择加氢站信息;NFCEV为燃料电池汽车总数。
2 优化调度模型
2.1 分布鲁棒优化模型
本文所提调度模型含风电出力不确定性变量,以电-氢综合能源系统运行成本Cop最低为目标,包括机组运行成本、机组启停成本、加氢站运行成本、系统与上级主网电能交互成本、弃风成本。加氢站运行成本包括电解槽启停成本、电解槽运行成本以及通过售氢收益之差。
2.2 约束条件
1)燃气轮机约束
2)加氢站约束
式中:pt,e为t时刻电解槽e的出力和分别为其上、下限;prampe为电解槽e的爬坡功率。式(25)为电解槽功率上下限约束;式(26)为电解槽爬坡约束。
3)主网购电与弃风约束
2.3 基于Wasserstein 距离风电不确定性建模
由于风电不确定性会对系统经济运行产生负面影响,因此在优化调度时需要纳入考虑。为了找到在最恶劣的不确定性概率分布场景下的最优调度,而分布鲁棒优化结果在经济性和保守性表现出良好的性能,分布鲁棒优化需要解决如何通过历史数据构造模糊集的问题。目前常见的模糊集构建有两种,分别是矩估计和概率距离,在本文中采取Wasserstein 距离构建风电预测功率不确定性模糊集。采取数据驱动的方式构建基于Wasserstein 距离模糊集,不需要任何先验信息且可以保证位置分布向真实分布收敛。
本文假设风电预测误差是zi。由于风电预测误差zi的实际概率分布不能获取,而可以从历史数据中获得预测误差样本集的经验分布,构建一个以经验分布为中心的概率球,认为预测误差的真实分布在这个球中。为了确定样本集误差分布与实际误差分布的距离,引入Wasserstein 距离来测度φzi与之间的距离D:
式中:Π表示联合分布;Nsam为风电预测功率样本数量和zi分别为实际风电功率预测误差和样本误差;和φzi分别为和zi的边缘分 布;‖ · ‖是 一 个范数函数,为了便于模型求解,这里使用1-范数;Ω为的 概 率 分 布 空 间;dzi为 关 于zi的 狄 拉 克 测 度。
进一步构建模糊集wzi:
式中:RΞ为支撑集Ξ中的全部概率分布,模糊集为一个Wasserstein 球体;ε为Wasserstein 球体的半径,通常来说它是一个样本大小相关函数,随着样本量的增加而减小。
根据文献[24],可得一个经验表达式为:
式中:b为置信水平;δ为参数;zi,n为第n个不确定性参数为数 据样本平 均值。
2.4 优化调度模型转化
为简化分析,将目标函数式(22)改写为如下矩阵形式:
式中:EQ(·)表示期望函数;x为决策变量;cT为目标函数中决策变量对应的系数矩阵;d表示常数部分;sup(·)表示求上确界函数;h(x)和ho(x)分别为约束条件中含有不确定性参数的函数和仅含决策变量的函数对应式(2)至式(28)的约束条件;对应仿射策略下含不确定性变量的所有约束条件。目标函数是指在模糊集wzi最恶劣条件下内层期望函数和运行成本最小。
根据文献[25],其中含不确定性变量内层函数可以改写为如下形式:
式中:λ为对偶变量为第i个样本;k为误差样本数;ωi为辅助变量。
内层分布鲁棒函数模型经过转化得到最终的混合整数线性规划模型为:
3 算例分析
本文选取IEEE 33 节点配电网和24 节点Sioux Falls 交通网络来构建电-氢交通耦合系统,具体结构见附录A 图A2 和图A3。配电网节点1 与上级主网进行购电,燃气轮机位于节点8 和18,4 个加氢站分别位于配电网的节点15、22、25、31 与交通网节点1、13、15、18。风机位于加氢站内部,燃气轮机、电解槽设备相关参数见附录A 表A1 和表A2。分时电价参数见文献[26],电负荷预测曲线见附录A 图A4。各时段车流缩减比例见附录A 图A5。调度模型通过强对偶理论等价转化为混合整数线性规划(MILP)问题,并通过与传统鲁棒优化和随机优化进行对比,验证所提方法有效性。本文采用MATLAB 2021b平台通过Yalmip 调用Cplex12.9 进行求解,计算机参数为Intel Core i5-8400 2.80 GHz CPU,8 GB内存。
3.1 电-氢综合能源系统优化调度分析
附录A 图A6 给出了当天主网购电、燃气轮机、加氢站消耗电能制氢调度结果。从图A6 可以看出,系统在电价较低的时候向主网进行大量购电,并且购电大都发生在白天,这是由于风电在白天处于较低的功率水平,需要通过上级主网购电来满足系统内的电负荷需求。由于节点8 的负荷最高且传输功率及节点电压安全约束的限制,因此该处的燃气轮机一直以额定功率运行。位于节点18 的燃气轮机在01:00—06:00 时段处于停机状态是由于此时风电功率较高造成的,而此时系统电负荷降低;在10:00—12:00 和19:00—21:00 时段,系统电负荷达到一天的峰值,此时燃气轮机功率升高来满足系统电负荷平衡。而加氢站根据风电的出力水平,分时电价为了自身的收益最大,电解槽出力最大发生在交通流量早高峰之前,在电价较高时选择停止制氢,全部使用储氢罐中储存的剩余氢气。
3.2 分布鲁棒优化模型下加氢站运行策略
图2 给出了分布鲁棒优化模型下4 个加氢站的制氢情况,其中,红色和蓝色折线图分别反映了生产和消耗氢气量的趋势情况。以3 号加氢站为例,位于配电网节点31 和交通网节点15 的3 号加氢站,根据HFCV 路径优化模型得到加氢站预测负荷曲线,见附录A 图A7。加氢负荷呈现双高特征,符合上下班高峰情况,负荷峰值发生在08:00 和18:00。电解槽工作时间集中在00:00—09:00 与15:00—24:00时段,上述时段电价较低且风电出力较大,因此安排电解槽集中工作在上述时段,并且在06:00 达到满功率运行,以应对即将到来的早高峰。00:00—06:00 时段电解槽运行功率普遍高于下午和晚上,下午电解槽运行功率不会出现激增和骤降,始终维持在最低出力水平左右,这对于电解槽的运行寿命有利,比较符合实际情况。
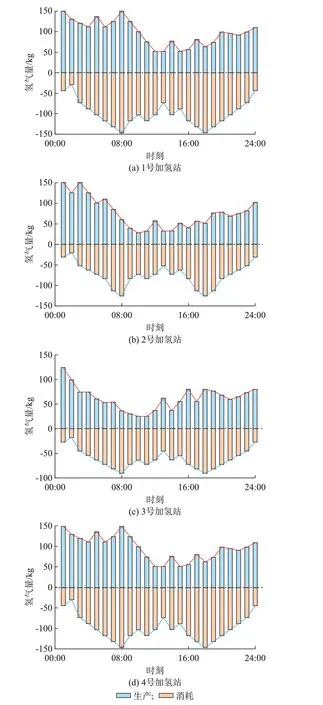
图2 加氢站制氢情况Fig.2 Result of hydrogen production of hydrogen refueling stations
对HFCV 路径优化模型进行求解,图3 给出了16:00 时的交通网道路拥堵程度,在晚高峰时段16:00 时的交通网流量分布如图4 所示。图中:黑色数字表示道路编号,红色数字表示该条线路上的交通流量。

图3 16:00 交通网拥堵程度热力图Fig.3 Heat map of traffic network congestion at 16:00

图4 16:00 交通网车流量分布Fig.4 Distribution of traffic flow at 16:00
由图4 可知,HFCV 用户会选择道路等级高、容量较大的外环线路16、17、19、54 和56 作为行驶路线。从图3 可知,道路16 和19 发生了轻微的拥堵,其原因在于车流量超出了它的承载能力时,道路阻抗将增加。其他的HFCV 用户感知该线路阻抗增加后会通过改变行驶路径减小自己的出行成本并缓解堵塞现象。在内部道路中,线路37 和57 具有较大的交通流量,其原因在于这些道路毗邻加氢站,当HFCV 氢气量达到一定阈值时会选择最近的加氢站进行加氢来保证出行,HFCV 聚集在加氢站附近导致道路流量增加,验证了HFCV 路径优化模型对于车辆路径调整的有效性。
3.3 不同优化模型结果对比分析
为了验证本文提出的分布鲁棒优化模型的优势,选取随机优化、鲁棒优化作为对比模型。设置3 种情景进行对比仿真。
情景1:考虑风电功率预测误差不确定性的随机优化模型。
情景2:考虑风电功率预测误差不确定性的鲁棒优化模型。
情景3:考虑风电功率预测误差不确定性的分布鲁棒优化模型(本文所提模型)。
不同优化模型下的运行成本如表1 所示。
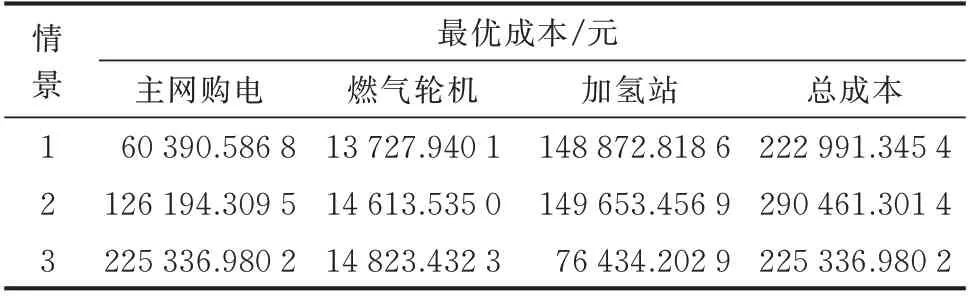
表1 不同优化模型下运行成本Table 1 Operation costs of different optimization models
从表1 可以看出,情景1(采用随机优化模型)系统的总成本最低,而情景2(鲁棒优化)系统运行成本最高。随机优化需要事先已知不确定性变量分布函数,在实际运行过程中很难已知变量的分布情况,因此所得出的调度方案并不可靠。鲁棒优化模型运行成本最高是由于鲁棒优化考虑最恶劣场景下的运行情况,忽略了一些样本分布信息,鲁棒优化模型下所得出的购电、制氢方案均偏保守。本文所提出的分布鲁棒优化模型运行成本介于两者之间,其中,分布鲁棒优化相比鲁棒优化成本降低了22.4%,运行成本较随机优化高出1%,这是因为分布鲁棒优化模型考虑了模糊集中最差场景分布,调度结果在保守与乐观之间达到均衡。附录A 图A8 展示了不同样本量下Wasserstein 半径值和目标函数值的情况。可以看出,随着样本量的增加,半径值和目标函数值总体呈现下降趋势,最终收敛到稳定值附近,这是因为此时样本量比较大,使得模糊集越来越接近于真实分布,分布鲁棒优化模型考虑了风电出力所有场景下分布情况所做出的决策更加稳定。
为了验证所提方法的有效性,图5、附录A 图A9 至图A11 分别为随机优化、鲁棒优化和分布鲁棒优化模型加氢站运行结果对比图。从图5 可以看到,随机优化无须考虑最恶劣场景下的预测误差分布情况,因此所得到调度结果比较乐观,通过在电价低谷时电解槽运行增加功率,在电价高峰时电解槽运行功率维持在较低的运行工况下,来确保加氢站运行成本最低。
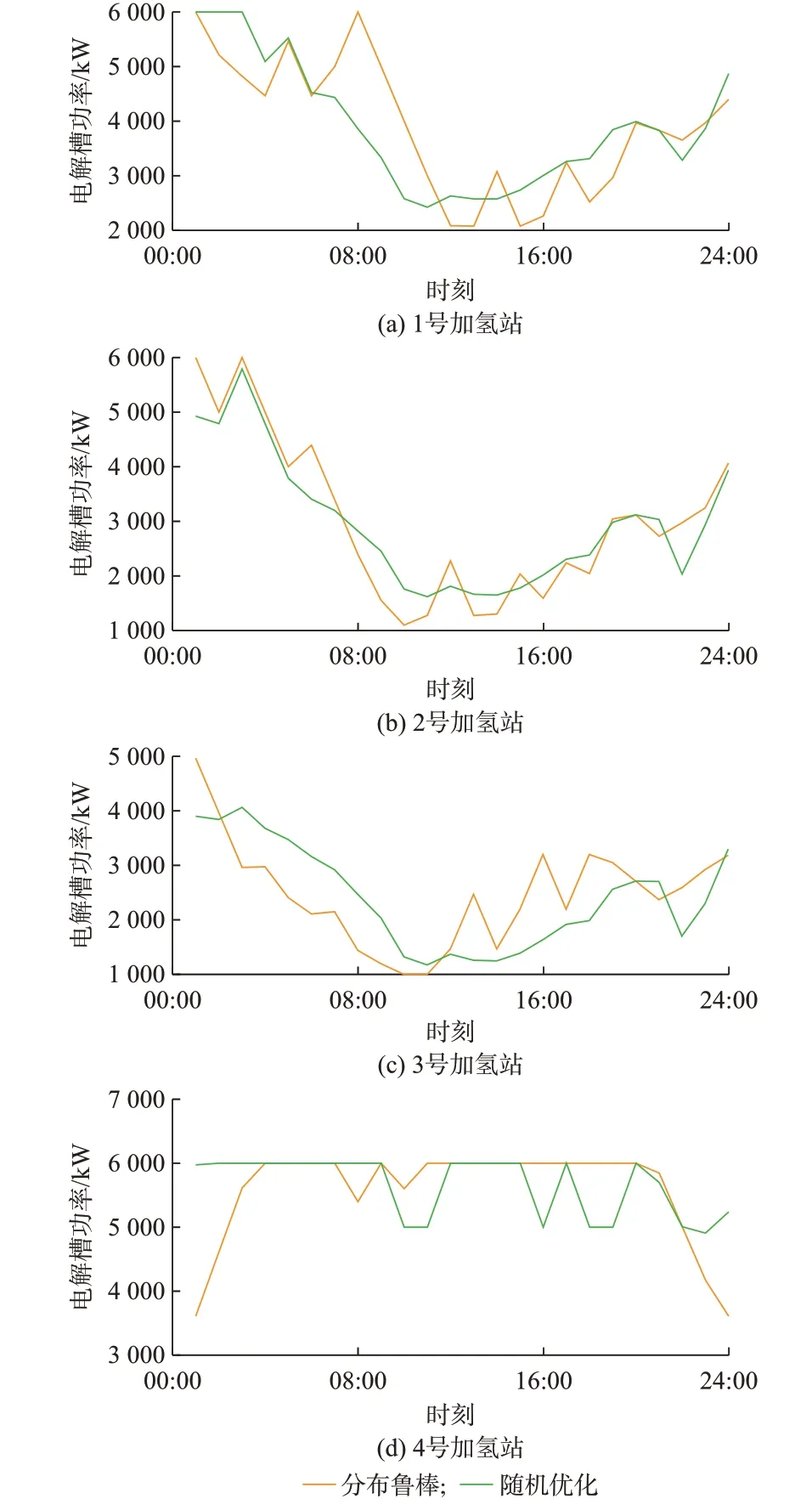
图5 分布鲁棒优化和随机优化加氢站调度结果对比Fig.5 Comparison of scheduling results for hydrogen refueling stations with distributionally robust optimization and stochastic optimization
从附录A 图A11 可以看出,鲁棒优化下加氢站的调度结果相比分布鲁棒优化更加保守,鲁棒优化模型下加氢站消耗电能大部分时候大于分布鲁棒优化模型下调度结果,以确保氢能供应,这也会产生较高成本,而分布鲁棒优化模型可以更好地兼顾经济性与鲁棒性。
4 结语
本文考虑HFCV 加氢负荷的电-氢-交通网络耦合系统协同优化运行模型,基于用户出行需求,采用Dijkstra 算法确定HFCV 行驶路径,并且给出HFCV 加氢规则,得到计及加氢行为下交通流量分配模型与配电网负荷模型,基于Wasserstein 距离构建风电功率预测误差模糊集处理不确定性。本文所得结论如下。
1)在新型电力系统中,考虑电-氢转换特性,引入加氢站与HFCV 作为可调度的主体,在新能源出力较高时,通过电解制氢供给HFCV 进行加氢缓解里程焦虑,进一步增加HFCV 参与交通网运行可以降低电力系统中碳排放量以及弃风量。
2)基于Wasserstein 距离构建风电功率预测误差模糊集,处理可再生能源不确定性,通过强对偶理论将分布鲁棒优化模型转化为混合整数线性规划模型。与常规的随机优化和鲁棒优化相比,分布鲁棒得出的调度方案在保守和乐观之间得到平衡,并且分布鲁棒优化模型下系统运行成本相比鲁棒优化降低了22.4%
需要指出的是,本文中所提出的考虑HFCV 加氢负荷的电-氢能源系统协同优化模型在调度过程中认为加氢站与服务商是利益共同体,因此调度结果偏向用户侧,如何在调度模型里面考虑不同加氢站主体利益分配以及交通网络流量均衡问题将成为后续研究的重点。
附录见本刊网络版(http://www.aeps-info.com/aeps/ch/index.aspx),扫英文摘要后二维码可以阅读网络全文。
