车载导弹发射架结构有限元分析与拓扑优化设计

牛草，顾广鑫，朱磊，徐宏斌，李正宇，张卫红，陈永伟，王博，石建雄，李一哲

(1.西安现代控制技术研究所， 陕西 西安 710065；2.西北工业大学 机电学院 航宇材料结构一体化设计与增材制造装备技术国际联合研究中心， 陕西 西安 710072)

0 引言

车载发射装置(见图1)是车载导弹武器系统的重要部件之一，通常由发射架、回转平台、俯仰与方位驱动模块等组成，主要用于承载并赋予导弹初始射向。发射装置结构必须具有足够的刚强度和合理的动力学特性，以保证可靠承载，避免结构变形和振动过大而影响导弹射击精度，从而确保车载武器系统完成快速机动、地面突击等作战任务[1]。

图1 某车载导弹发射装置[2]Fig.1 A vehicle-borne weapon launcher[2]

随着自动化、信息化、智能化和电池等技术的发展，车载武器正逐渐向无人化和电驱动方向发展[3]，其高机动、长续航等要求日益凸显，这些新形势对包括发射装置在内的车载武器结构轻量化高性能设计提出了新的挑战。

传统武器装备结构设计以反复“设计- 分析- 加工装调- 试验验证- 改进”为主要手段。如图2所示，首先基于以往工程经验，针对不同载弹量和给定设计空间与质量等要求进行结构设计和布局，然后通过多次人工调整与校核分析获得可行设计方案，最后进行加工装调和试验验证，期间还可能进行多轮反复。该设计模式流程繁琐、研制周期长、费用高昂，且往往造成结构安全裕度过高和超重。

图2 武器装备结构传统设计流程Fig.2 Traditional structural design process for weapons

得益于现代计算机技术与计算力学等相关学科的发展，在图2中武器装备研制过程的分析阶段，设计人员利用有限元等数字化仿真手段对结构性能进行评估的做法已较为普遍。张永存等[4-5]将有限元法应用于典型火炮结构的静动性能分析，对炮架和前支架进行了改进设计，提高了结构刚度，降低了炮口最大振幅和发射扰动，有助于提高射击精度。薛海瑞等[6]采用混合仿真方法，将有限元数值分析与模态试验相结合，根据试验采集数据对有限元模型进行修正，提高了某导弹发射架在冲击载荷下的分析准确度。

上述做法在一定程度上提高了产品设计效率，节约了试制和试验测试费用，但仍较大程度地依赖于工程经验，需手动进行大量方案调整和有限元分析校核工作，难以满足武器装备日益增长的结构高性能轻量化创新设计需求。

结构优化技术作为数学最优化理论和计算力学、计算机技术等多学科相融合而发展形成的设计方法，为设计人员提供了有效的结构创新设计工具。根据设计变量定义的不同，结构优化可以分为尺寸优化、形状优化和拓扑优化3个层次[7]。其中，拓扑优化以优化材料空间布局为出发点，实现结构构型的创新设计，突破了尺寸和形状优化的局限，在结构减重和充分挖掘结构承载潜力方面具有巨大优势。在过去的30余年中，拓扑优化不仅在学术界蓬勃发展，形成了包括密度法、水平集法等在内的多种实施方法[8]，而且在航空、航天、汽车等领域的结构轻量化创新设计中应用日益广泛[9-10]。近年来，结构拓扑优化技术在火炮[11-14]、导弹[15-17]、火箭弹[18-20]等兵器装备研制中也越来越得到重视。

其中，代表性工作有：王显会等[11]对火炮载车的承力车架进行拓扑优化设计，考虑了越野行驶与火炮发射等引起的多种冲击载荷工况，获得了满足刚强度和振动要求且紧凑质轻的车架结构设计；张海航等[12]利用Altair OptiStruct对火炮上架进行拓扑优化，在提高刚度的同时获得了减重12.17%的优化效果；孙全兆等[13]考虑火炮最大射角工况，先利用拓扑优化得到火炮上架的最佳传力路径，再用尺寸优化对重构模型的主承力板件进行详细设计，获得了刚强度明显改善的上架优化设计方案；孙玲庆等[14]针对某火炮自动装填系统的翻板机构回转臂在弹药交接过程存在变形和应力较大的问题，用ANSYS Workbench软件进行拓扑优化计算，取得了刚强度均优于原有设计且减重26%的有益效果；刘瀚超等[21]结合多体动力学与拓扑优化，对某车载地空导弹发射装置托架进行结构优化，在结构减重28.6%的情况下，优化设计的比刚度结构效能和1阶模态频率均得到大幅改善，对降低导弹初始扰动起到了良好作用。

在导弹结构设计中，Luo等[15]将折中规划法和多层序列凸规划方法结合，考虑了气流差异引起的气动载荷、轴向过载、助推器推力和主发动机推力4个工况，对巡航导弹弹体结构进行结构刚度和固有频率最大化的多目标拓扑优化设计。Jiang等[16]对导弹发动机支撑架进行拓扑优化，并通过激光固化成型3D打印进行快速原型制造，用力学加载试验对优化设计进行了验证。温晶晶等[17]对某导弹整体式翼面骨架结构进行拓扑优化设计，获得了满足结构强度和刚度要求的轻量化弹翼骨架模型。

另外，杨翠东等[18]、孙延超等[19]和刘晴等[20]分别对火箭武器发射箱、火箭弹发射装置回转箱体和火箭炮底架结构进行了考虑多工况的拓扑优化设计，均获得了较大幅度减重的优化效果。

本文针对某车载导弹发射架结构的轻量化设计问题，首先分析其主要受载工况，采用有限元法进行数值仿真计算，讨论发射架结构受载特点，据此总结出了导弹装填、卸载和发射作业序列规划的指导原则。在Altair HyperMesh软件中建立发射架的多工况拓扑优化模型并利用Altair OptiStruct软件进行求解，研究不同制造和尺寸约束对拓扑优化构型的影响。根据拓扑优化构型提供的主传力路径，提取结构特征，对发射架进行重构设计。有限元校核分析表明，相比原有设计，优化设计后的发射架结构在质量降低的情况下，刚度、强度和固有频率均有提升。

1 发射架受载工况分析

发射架通常是发射装置的关键承力部件，肩负着承载弹药和其他相关设备的重要作用，其刚度直接决定着发射装置的整体刚度。图3所示为某车载导弹发射架原有设计的简化模型，结构形式整体上关于Oyz平面对称，主要由2条主横梁、2条主纵梁、1条后部副横梁、4条副纵梁以及中部菱形布局的小斜梁和小横梁通过焊接而成。发射架通过两侧的前后轴座安装在负载平台上。各梁均采用国家标准GB/T 3094—2012冷拔异型钢管规定的矩形钢管型材，其截面如图4所示，图4中H和A为边长，R为外圆角半径，s为壁厚。导弹通过图3中略高于各梁的凸台安装于发射架上，导弹质量和过载载荷均通过凸台传递到发射架上，而不与前后两条主横梁之间的主副纵梁、小斜梁、小横梁以及副横梁等发生接触。实际结构中，凸台部位开有安装孔，为便于有限元建模，对其进行了简化处理。

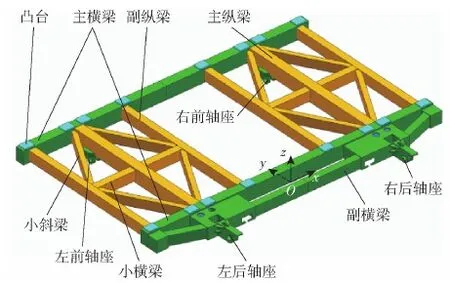
图3 发射架结构原有设计Fig.3 Original design of the launching cradle

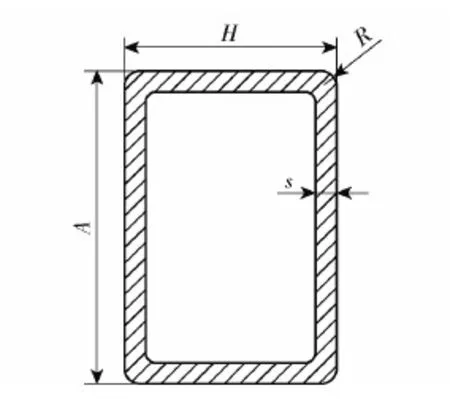
图4 GB/T 3094—2012规定的矩形钢管型材截面Fig.4 Cross-section of the profiled steel tubes in accordance with GB/T 3094—2012

该发射架主要有随载车行军和发射作业两种工作状态。随载车行军时，发射架仰角为0°，承受的载荷包括发射架自重、导弹质量以及载车行军造成的过载；在发射作业时，发射架升起某个角度(见图1)，承受发射架自重、导弹质量以及导弹发射后坐等载荷。其中，导弹发射后坐相比于行军过载相对很小，因此本文忽略了导弹发射工况载荷，主要考虑随载车行军的过载工况。表1列出了该发射架随载车行军过程中主要承受的7个典型过载工况，各行军过载工况的取值一方面是根据工程研制中的实际数据和经验，另一方面借鉴了类似车载装备的相关理论分析[22]，具体情况如下：

1)工况1表示发射架仅承受弹药和发射架本身的自重，其中重力加速度g取10 m/s2；

2)工况2和3分别表示发射架承受沿图3中z轴的负向和正向5g过载，代表载车在快速通过凹坑或凸起造成的垂直于地面(见图3中的z轴)的过载；与重力叠加后分别为沿图3中z轴方向的-6g和+4g过载；

3)工况4和5分别表示发射架承受沿图3中x轴的负向和正向5g过载，同时承受弹药和发射架的自重，代表载车在高速转弯时引起的垂直于车体纵轴(见图3中x轴)的横向过载；

表1 发射架过载工况Table 1 Overloading conditions of the launching cradle

4)工况6和7分别表示发射架承受沿图3中y轴的负向和正向5g过载，同时承受弹药和发射架的自重，代表载车在行驶过程中的快速启动和紧急刹车两种情况造成的沿车体纵轴方向(见图3中的y轴)的过载。

表2汇总了发射架在服役过程中可能的载弹量及装弹分布情况，这里称为载弹工况。

共有15个载弹工况，具体情况如下：

1)载弹工况(a)：发射架满载4发导弹；

2)载弹工况(b)～(e)：发射架承载3发导弹；

3)载弹工况(f)～(k)：发射架承载2发导弹；

4)载弹工况(l)～(o)：发射架承载1发导弹。

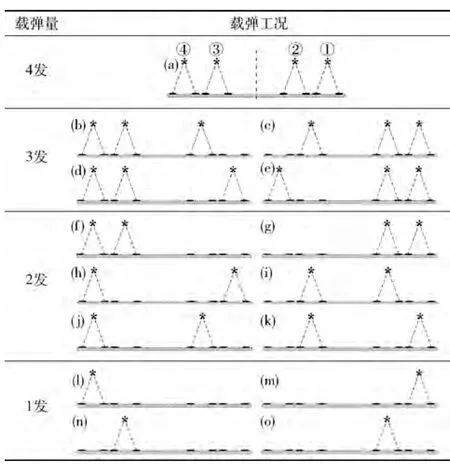
表2 发射架载弹工况

值得注意的是，载弹工况(b)和(c)、(d)和(e)、(f)和(g)、(j)和(k)、(l)和(m)、(n)和(o)分别关于Oyz平面对称，而发射架结构也关于Oyz平面对称，即结构与载荷均具有对称性，因此上述成对的工况可以仅考虑其一。在有限元分析时，仅需考虑(a)、(b)、(d)、(f)、(h)、(i)、(j)、(l)和(n) 9个载弹工况。

2 发射架原有设计有限元分析

为研究发射架受载特点，对发射架原有设计在不同过载和载弹工况的组合下进行有限元建模与分析。

2.1 发射架有限元建模

如图5所示，将发射架原有设计的三维几何模型导入Altair HyperMesh软件中，建立有限元模型。采用四面体单元对几何体进行网格划分，同时启用基于实体邻近度和表面曲率的自适应网格剖分策略以保证网格质量，设置最小和最大网格尺寸分别为2 mm和10 mm。得到的有限元模型单元数为426 990，节点数为1 569 194。将导弹简化为CONM2质量点单元，并通过RBE3单元连接到导弹安装凸台上。图5给出了载弹工况(a)情形下的有限元模型，将图中4个弹位从右至左依次编号为①、②、③、④。施加图6所示的位移边界条件，即约束前后耳轴孔周节点径向自由度，以及耳轴座端面节点的x向自由度。有限元分析时共涉及63个不同过载和载弹工况组合下的有限元模型。

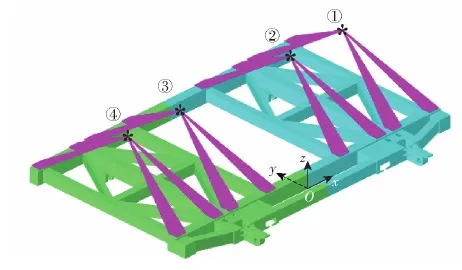
图5 发射架结构原有设计在载弹工况(a)时的有限元 模型(“*”表示所承载导弹的等效质量点)Fig.5 Finite element (FE) model of the original design of the launching cradle under the missile-carrying condition (a) (The asterisks “*” indicates the equivalent mass points of the borne missiles and the same would apply hereinafter)

图6 发射架有限元模型的位移边界条件(“*”表示 所承载导弹的等效质量点)Fig.6 Displacement boundary conditions of the FE model for the launching cradle

发射架材料为结构钢，杨氏模量为210 GPa，泊松比为0.3，材料密度为7 850 kg/m3。原有设计的质量为285.32 kg。

2.2 有限元分析结果与讨论

表3、表4和图7对比了不同过载和载弹工况下发射架的最大总位移。发射架在载弹工况(a)下总位移的分布云图见表5第2列。由表3和表4可以看出，除载弹工况(i)的最大位移发生在垂向过载工况之外，对于其他载弹工况，发射架均是在承受横向过载工况时的结构变形最大。

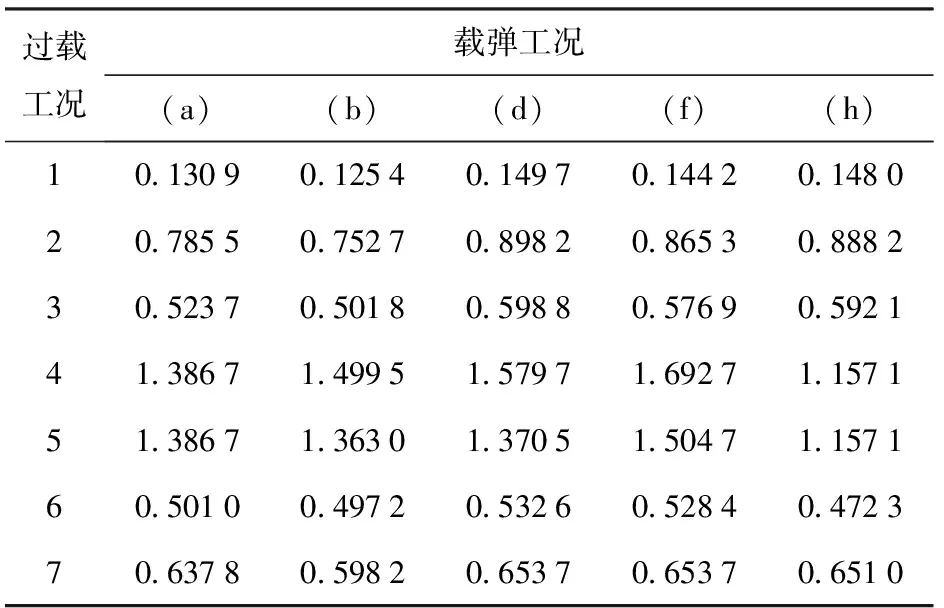
表3 载弹工况(a)～(h)下发射架原有设计 结构变形Table 3 Structural deformations of the original launching cradle under the missile-carrying conditions (a)～(h) mm

表4 载弹工况(i)～(n)下发射架原有设计 结构变形Table 4 Structural deformations of the original launching cradle design under missile-carrying conditions (i)～(n) mm

图7 发射架原有设计在不同过载和载弹工况下 结构变形对比Fig.7 Comparison of structural deformations of the original launching cradle under different overloading and missile-carrying conditions

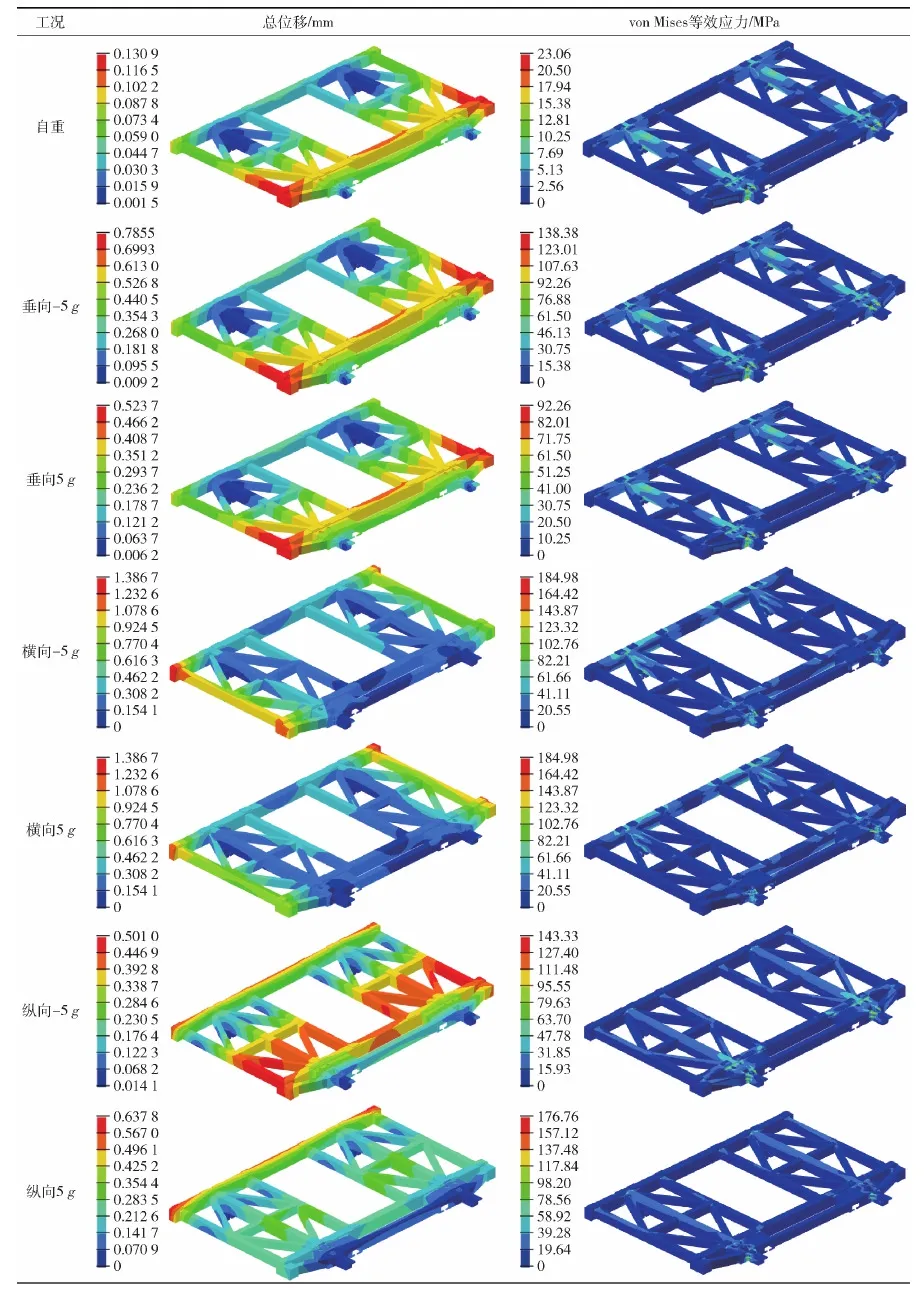
表5 原有设计在载弹工况(a)下的有限元分析结果云图

在载弹量相同的情况下，装弹布局对结构变形的影响非常大。例如，对于装载1发弹的载弹工况(l)和(n)，前者在各过载工况下的结构变形为后者在相同过载工况下的2倍左右。另外，对于装载2发弹的载弹工况(f)和(i)，前者在横向-5g过载下的变形为1.692 7 mm，是后者在相同过载下变形(0.341 5 mm)的5倍。

尤其值得注意的是，最大变形量并非出现在发射架满载的载弹工况(a)下，而是出现于装载2发弹的载弹工况(f)。同时承受横向-5g过载的情况下，后者的结构变形比前者在相同过载下高出22%。究其原因，在同样装载2发弹的情况下，载弹工况(f)中的2发弹全部装载在Oyz对称面的一侧，可见装弹不对称带来的偏载对发射架造成了较大的承载负担。

基于上述论述，可以总结出导弹装填、卸载和发射作业序列规划的指导原则：在装填导弹时，应优先向靠近Oyz对称面的②、③弹位装填，然后向外侧的①、④弹位装填；反过来，在卸载或发射导弹时，应优先卸载或发射①、④弹位，之后再卸载或发射②、③弹位。这样可以使载弹行军过程中所承载弹药的整体质心尽量靠近Oyz对称面，从而达到减小发射架结构变形的目的。

表6和表7给出了发射架在各载弹与过载工况下的最大等效应力。载弹工况(a)下的等效应力分布云图如表5第3列所示。发射架在满载工况(即载弹工况(a))下承受横向±5g和纵向5g过载时，结构的等效应力水平相对较高，最大达到了185 MPa。

表6 载弹工况(a)～(h)下发射架原有设计 等效应力Table 6 Equivalent stresses of the original launching cradle under the missile-carrying conditions (a)～(h) MPa

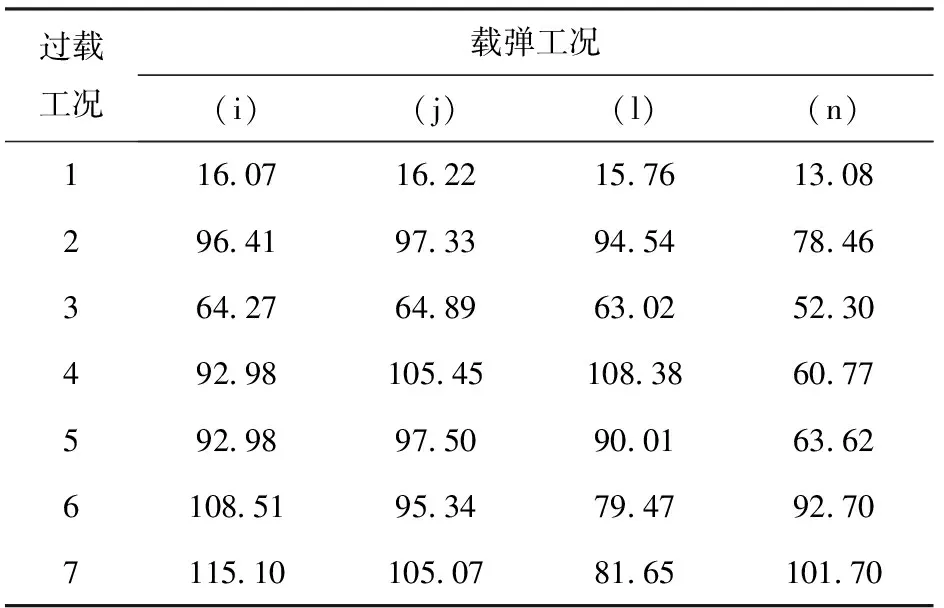
表7 载弹工况(i)～(n)下发射架原有设计 等效应力Table 7 Equivalent stresses of the original launching cradle under the missile-carrying conditions (i)～(n) MPa

3 拓扑优化基本理论

本着“物尽其用”的基本出发点，结构拓扑优化本质上是在给定设计域内寻求材料的最佳分布，使指定结构性能达到最优，同时满足设计约束的优化问题[9，23-24]。相比于水平集等其他方法，基于SIMP(Solid Isotropic Material with Penalization)模型[25]的变密度拓扑优化方法较为简洁和易于实施，目前已被集成到多个商用有限元软件(如Altair HyperWorks、ANSYS等)中，且在工程中得到较广泛的应用[9]。本文采用Altair HyperWorks软件包中的OptiStruct模块进行拓扑优化。变密度拓扑优化方法的基本思想是在有限元法的基础上，先将结构离散为有限个相对独立的单元，然后对每个单元定义一个独立变化的设计变量，该设计变量反映着单元的相对密度，即伪密度设计变量。伪密度为0(或接近0)表示对应的单元处应为孔洞，其对应的材料可以去除；伪密度为1(或接近1)则表示对应的单元处为实体，该处的材料需要保留。SIMP材料插值模型使伪密度取值允许在[0，1]上连续变化，将原始的整数规划问题转化为相对较易求解的连续非线性规划问题。通过梯度优化算法对设定的优化目标在设计约束下寻优，去除承载效率低的材料，获得优化的材料拓扑布局，实现结构轻量化概念设计。

对于某一载弹工况，考虑表1所述多个过载工况的发射架拓扑优化数学列式可以写为

(1)

3.1 材料插值模型

经典SIMP材料插值模型可以写为

(2)

式中：P(ηi)为插值函数；Ei0为第i个单元在完全实体状态(ηi=1)下的弹性模量；p为惩罚系数，其通常取值为3。本文涉及的过载载荷属于惯性载荷，在处理此类设计相关载荷时，由于材料质量和刚度的描述不匹配，经典SIMP模型会导致低密度单元出现畸变。这里简要说明其原因：将材料密度记为ρ，则第i个单元的质量为

mi=ηiρVi

(3)

根据文献[26]，单元质量与刚度惩罚系数之比定义为

(4)

由于p通常取值为3>1，rmK在ηi取值趋近于0时将趋向无穷大，意味着单元刚度是其质量的高阶无穷小，引起单元局部变形过大，造成优化失败。

为解决这一问题，这里采用Zhu等[27]提出的多项式插值模型，

(5)

式中：w为线性项的权系数，通常取值为0.062 5。

相应地，rmK变为

(6)

此时由于分母中w的存在，无论ηi在[0，1]上如何取值，rmK均为有限大小。如此便可以有效解决经典SIMP模型的局部变形问题。

3.2 灵敏度分析

采用梯度算法求解式(1)所描述的优化问题，需要对加权柔顺度和体分比等进行灵敏度分析。根据式(3)，惯性载荷与质量直接相关，其有无和大小直接取决于材料分布情况。即设计变量ηi的改变不仅会引起刚度的变化(见式(2))，还会影响载荷的大小，因此在灵敏度分析时必须考虑载荷关于设计变量的灵敏度。灵敏度计算公式的推导过程遵循链式求导法则。限于篇幅，本文略去了具体公式及推导过程，读者可参阅文献[7,27-28]。

4 发射架结构拓扑优化设计

对发射架结构进行拓扑优化设计的基本思路是：首先建立发射架拓扑优化的有限元模型，通过在给定体分比约束下最小化结构柔顺度获得拓扑优化构型；然后依照优化构型体现的主传力路径布置型材杆件，以获得降低结构质量、提高结构刚度的优化设计效果。

4.1 拓扑优化模型与优化参数

将图3中主副纵梁、小横梁和小斜梁所占的区域填满材料作为设计域，即图8中的黄色区域，同时保留为安装其他设备所预留的中空区域，建立发射架结构拓扑优化有限元模型。由于设计域的形状比较规则，对其采用六面体单元进行网格剖分；而非设计域形状较复杂，则采用四面体单元划分网格。整个模型的单元数为506 930，节点数为892 894；其中设计域单元数为317 044，节点数为287 304。

图8 发射架拓扑优化有限元模型(黄色部分为 设计域，绿色部分为非设计域)Fig.8 FE model for topology optimization of the launching cradle (The regions in yellow are designable while those in green are not)

考虑发射架满载的载弹工况(a)，体分比约束上限设置为0.25。为满足体分比约束，迭代开始时单元伪密度值设置为0.25。各过载工况的加权系数均取0.142 9(即1/7)。惩罚系数p取典型值3。另外，若两个相邻迭代步之间的目标函数相对变化小于0.001且满足所有设计约束，或者达到了指定的最大迭代步数100，则终止迭代过程。

4.2 拓扑优化结果

在Altair OptiStruct中求解式(1)所描述拓扑优化问题，经过30个步迭代步后收敛，得到的优化构型如图9所示。如无特殊说明，图9以及后文的拓扑优化构型图显示的均是伪密度大于0.5的单元。由图9(c)～图9(f)可以看出，优化构型为材料向两侧弹位中间集聚的盒型结构，上下板之间为以前支撑座为中心、与导弹安装凸台相接的竖筋状结构。虽然图9的拓扑优化结果具有一定的参考意义，但该盒型结构制造难度较大。

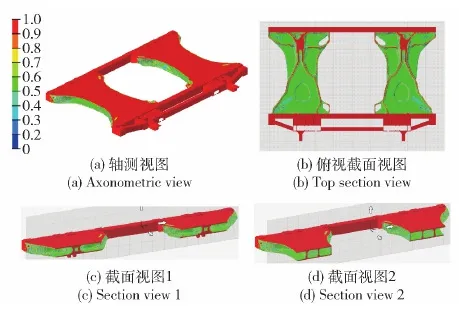
图9 无制造约束的拓扑优化构型Fig.9 Optimized topological configuration without manufacturing constraints

为获得主要由杆件组成的清晰拓扑优化构型，借鉴文献[29]中的做法，在求解式(1)所描述的优化问题时，额外施加挤压约束、最小尺寸约束与最大尺寸约束。挤压约束可以保证优化构型沿着某个方向形成一致的截面，该约束可以不受网格、边界条件或载荷的限制。最小尺寸约束意味着优化构型中结构杆件的最小截面尺寸不小于设定值，最大尺寸约束则使结构杆件的最大截面尺寸不大于设定值。施加最小尺寸约束主要是为了避免产生细小的结构特征，保证可制造性。施加最大尺寸约束能够避免大块材料的集中，有助于增加结构杆件的数量，分散传力路径，提高结构的冗余度，增强结构抵抗局部损伤的稳健性[30]。换言之，某个杆件受到局部损伤时不会导致整个结构的立刻失效，而是能继续承载。

图10为施加挤压约束后的拓扑优化构型，从中可以看出：材料向①、②弹位中间和③、④弹位中间集聚的趋势更加明显；①、②弹位中间和③、④弹位中间仅为一根较粗的跨过前后支撑轴的纵梁。

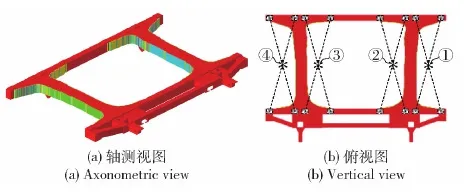
图10 施加挤压约束的拓扑优化构型Fig.10 Optimized topological configuration with extrusion constraints

图11、图12和图13给出了同时施加挤压约束和最大尺寸约束120 mm，并且最小尺寸约束分别为30 mm、40 mm和60 mm的拓扑优化构型。从图11～图13中可以看出：优化构型均形成了较为清晰且包含相比图9包含更多细节的材料走向和传力路径；随着最小尺寸约束值的增大，优化构型中的细小杆件逐渐减少。

图11 同时施加挤压约束和尺寸约束的拓扑优化构型： 最小尺寸约束30 mm，最大尺寸约束120 mmFig.11 Optimized topological configuration with extrusion constraints (minimum member size constraint at 30 mm and maximum at 120 mm)

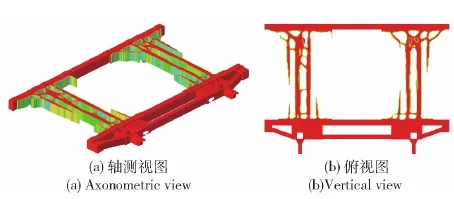
图12 同时施加挤压约束和尺寸约束的拓扑优化构型： 最小尺寸约束40 mm，最大尺寸约束120 mmFig.12 Optimized topological configuration with extrusion constraints (minimum member size constraint at 40 mm and maximum at 120 mm)

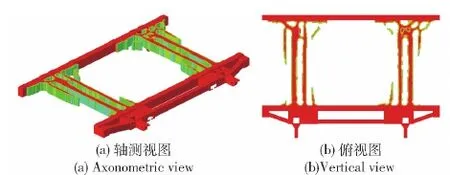
图13 同时施加挤压约束和尺寸约束的拓扑优化构型： 最小尺寸约束60 mm，最大尺寸约束120 mmFig.13 Optimized topological configuration with extrusion constraints (minimum member size constraint at 60 mm and maximum at 120 mm)

总体而言，图11～图13的优化构型具有以下特征：

1)整体上关于Oyz平面对称；

2)与图10类似，材料仍主要集中于①、②弹位中间和③、④弹位中间的位置；

3)图10中部的单根较粗杆件分化为两根纵梁；

4)纵梁与主横梁相连处根部形成了左右基本对称的较细斜支撑杆件。

表8汇总了上述拓扑优化迭代过程收敛时的加权柔顺度、体分比、迭代步数等数据。图14给出了加权柔顺度和体分比的迭代曲线。各优化迭代过程均在80步内收敛，且收敛时体分比约束均为主动约束。相比于不考虑制造约束的拓扑优化过程，额外施加制造约束时达到收敛需要较多的迭代步数，且收敛时的加权柔顺度更大。另外，随着最小尺寸约束的增大，收敛柔顺度逐渐增大。表明制造约束与结构刚度是互相制约的，在优化设计时需要对二者进行适当的权衡取舍。

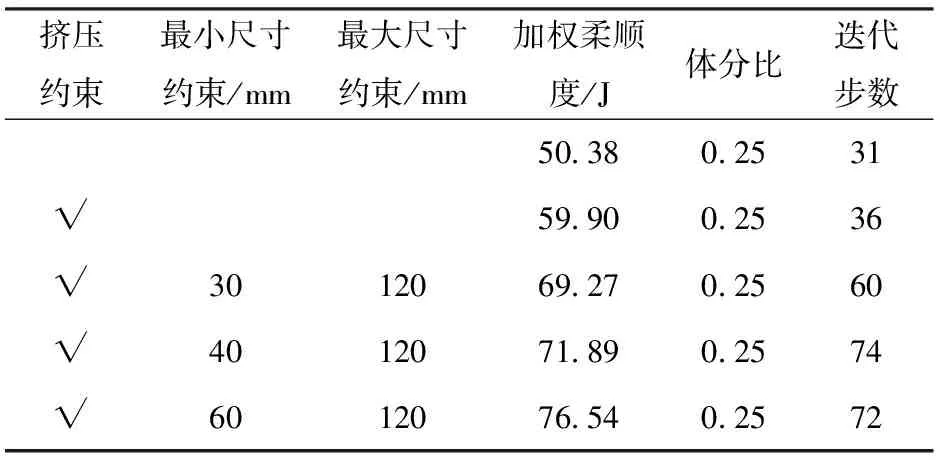
表8 拓扑优化迭代过程数据Table 8 Statistical data of the topology optimization processes

图14 拓扑优化中加权柔顺度和体分比的迭代曲线(圆 括号内数字分别表示最小和最大尺寸约束值)Fig.14 Iterative curves of weighted compliance and volume fraction in topology optimization processes. The numbers in the parentheses indicate the values of the minimum and maximum member size constraints, respectively

4.3 模型重构

根据4.2节的拓扑优化结果，从优化构型中提取主要结构特征，同时考虑制造成本和工艺性等因素，在三维造型软件中对发射架进行模型重构。

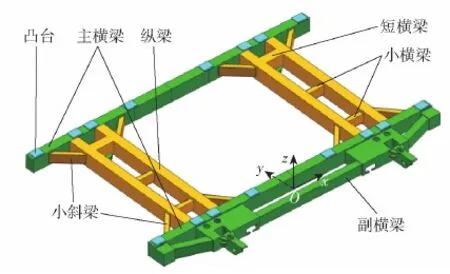
图15 根据拓扑优化结果重构的发射架优化设计模型Fig.15 Reconstructed model of the launching cradle based on the topology optimization results

如图15所示，分别在①、②弹位之间和③、④弹位中间布置两根截面如图4所示的纵梁。在左右前轴座相应位置布置与纵梁截面一致的短横梁，实现与前轴座连接并承载发射架及负载。为抵抗横向过载，在纵梁与主横梁相连的根部布置截面较小的小斜梁，在同侧两纵梁偏后部位布置两条小横梁。为减少备料种类、缩短采购周期、降低成本，纵梁采用截面与主横梁一致的型材杆件，所有小横梁和小斜梁采用相同截面的型材杆件。

根据拓扑优化构型重构设计后的发射架质量为254.82 kg，相比原有设计减重10.69%。

4.4 重构模型校核分析

为验证拓扑优化效果，对发射架优化设计进行与第2节相同的多种行军过载和载弹工况组合下的有限元校核分析。为保证可比较性，参照图5建立优化设计的有限元模型，即施加相同的边界条件，并采用相同的单元尺寸进行网格剖分，得到图16所示有限元模型。单元和节点数目分别为1 101 942和314 892。

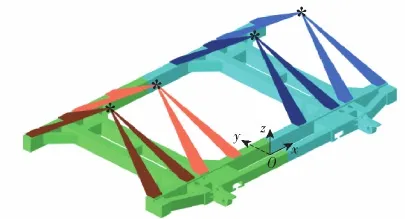
图16 发射架优化设计有限元校核分析模型Fig.16 FE model of the optimized design for verification

表9给出了发射架优化设计在载弹工况(a)下的总位移和等效应力云图。表10、表11和表12、表13分别列出了发射架优化设计的结构变形和等效应力分析结果，其中每行上方的数字表示分析结果，向下箭头“↓”和向上箭头“↑”分别表示相比原有设计有所降低和增加，其后的百分数为降幅或增幅。

由表10和表11可以看出，在大多数工况组合下，发射架优化设计的结构变形和等效应力都小于原有设计。原有设计的最大结构变形从载弹工况(f)在横向-5g过载下的1.692 7 mm降低为1.334 7 mm，降幅为21.15%。结构变形的最大降幅为21.47%，发生在载弹工况(f)承受纵向-5g过载情况下。同时注意到，在个别工况组合下，如载弹工况(h)和(l)在纵向5g过载下，结构变形相比原有设计稍有增大，增幅在1%左右。该类情况下的结构变形本身就较小，均小于0.5 mm，优化设计仍然满足设计要求。

表11和表12显示：发射架在大部分工况下的应力均有降低；在载弹工况(a)受横向过载情况下的最大应力从原有设计的184.98 MPa降为125.85 MPa，降幅达到31.97%。

图17对比了优化设计后的发射架在不同过载和载弹工况下的结构变形，从中可以看出，横向载荷下的结构变形仍普遍大于垂向和纵向过载。

表14对比了发射架原有设计与优化设计的固有频率。由表14可以看出，虽然在优化模型的目标和约束中均未考虑固有频率，但优化设计后前6阶固有频率提高幅度最大达到28.89%，其中第1阶固有频率提高了16.89%，这很可能得益于结构整体刚度的提升和质量的降低。

综上，优化设计以较少的材料用量获得了刚度和强度均优于原有设计的效果，显示了拓扑优化技术在结构轻量化高性能设计上的优势。

5 结论

本文基于有限元数值仿真法研究了某车载导弹发射架结构的承载特点，并利用拓扑优化方法对其进行了减重优化设计。得出主要结论如下：

1)通过多个过载和载弹工况的有限元分析结果对比研究，提炼出发射架实际使用过程中导弹装填、卸载和发射作业的重要指导原则：应使所承载导弹的整体质心尽量靠近Oyz对称面，以达到尽量减少发射架结构变形的目的。

2)运用基于密度法的拓扑优化方法对发射架结构进行了优化设计，得到了相比原有设计质量更轻且刚强度均得到大幅改善的优化设计，同时由于结构刚度的提升和质量的降低，发射架的固有频率也得到较大幅度的提升，优化效果明显。

3)在车载武器结构设计中采用拓扑优化方法进行概念设计，可以有效降低传统经验设计方法的盲目性，提高设计效率和设计质量，为车载武器结构轻量化高性能创新设计提供了重要借鉴。

4)拓扑优化设计后的发射架结构强度仍存在一定冗余，下一步研究可以采用尺寸优化技术对型材杆件的长、宽、厚等截面尺寸进行详细设计，在满足刚强度要求的前提下进一步降低结构重量。

表9 优化设计在载弹工况(a)下的有限元分析结果云图

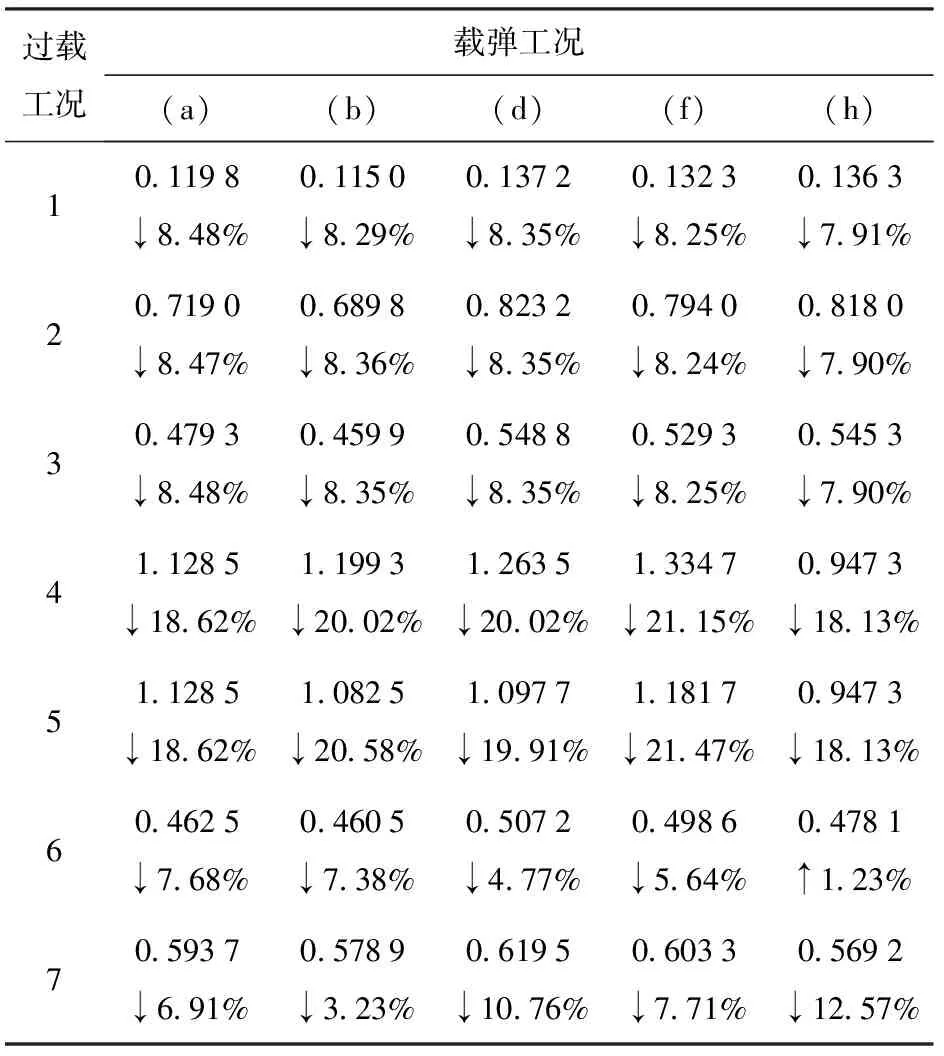
表10 载弹工况(a)～(h)下发射架优化设计 结构变形Table 10 Structural deformations of the optimized launching cradle design under the missile-carrying conditions (a)～(h) mm

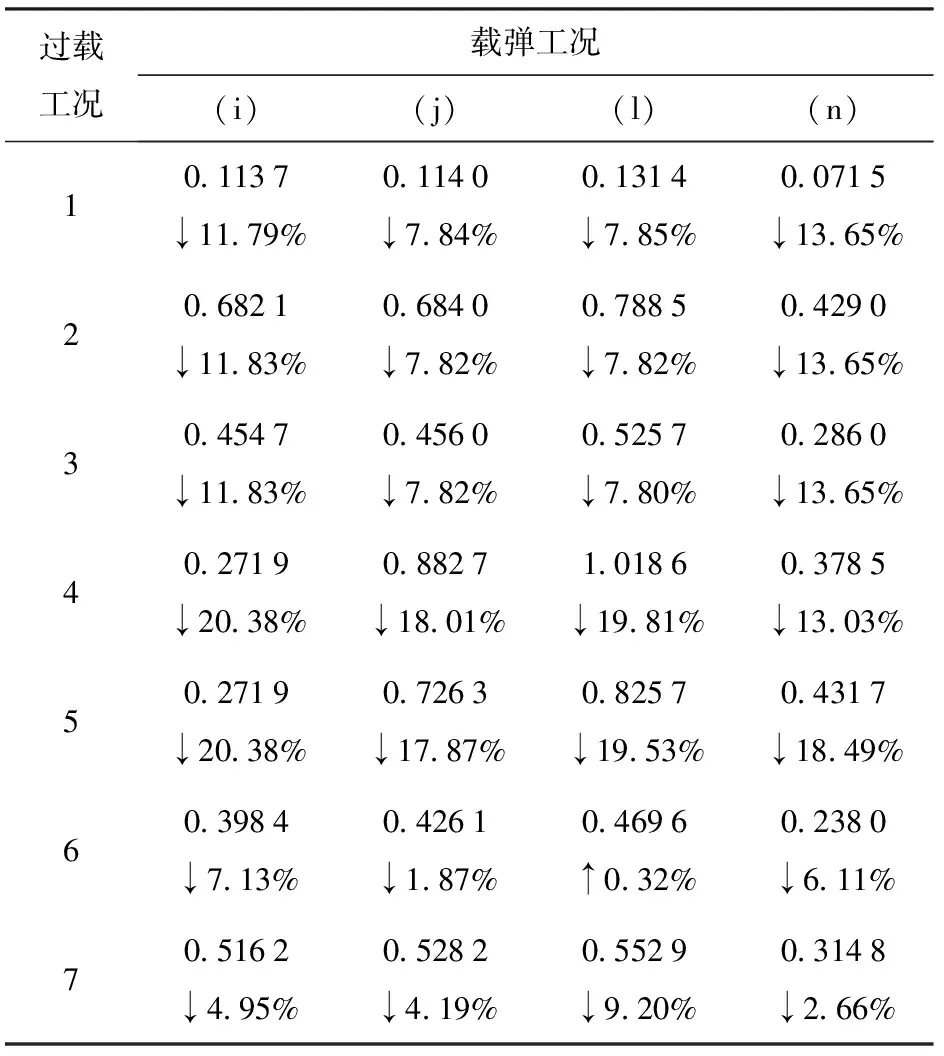
表11 载弹工况(i)～(n)下发射架优化设计 结构变形Table 11 Structural deformations of the optimized launching cradle design under the missile-carrying conditions (i)～(n) mm

表12 载弹工况(a)～(h)下发射架优化设计 等效应力Table 12 Equivalent stresses of the optimized design under the missile-carrying conditions (a)～(h) MPa

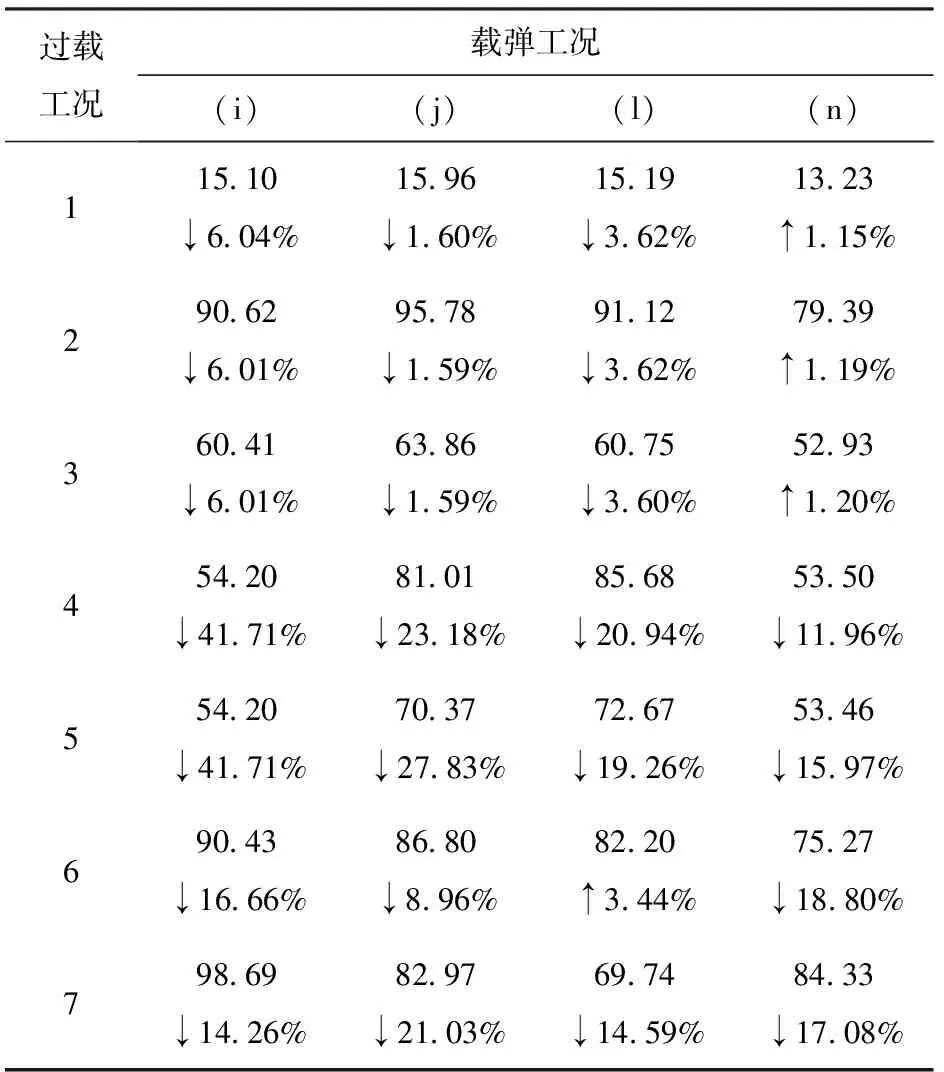
表13 载弹工况(i)～(n)下发射架优化设计 等效应力Table 13 Equivalent stresses of the optimized launching cradle design under the missile-carrying conditions (i)～(n) MPa

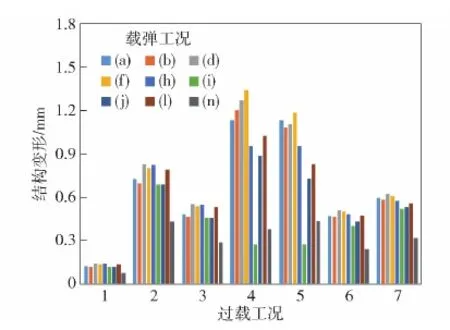
图17 发射架优化设计在不同过载和载弹工况下结构 变形对比Fig.17 Comparison of structural deformations of the optimized launching cradle under different overloading and missile-carrying conditions

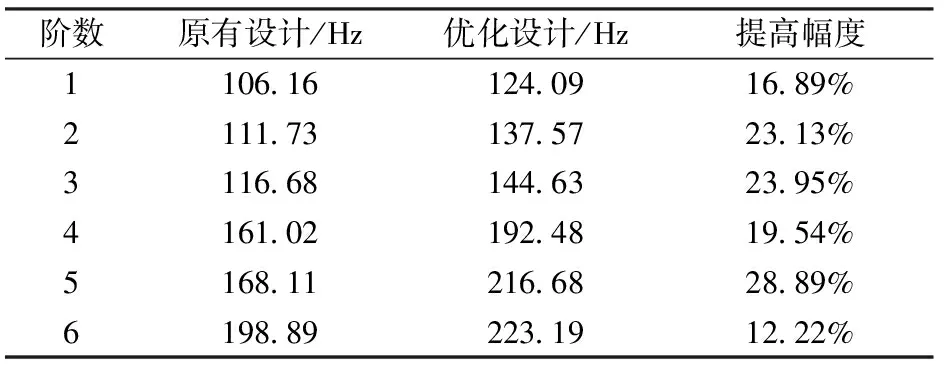
表14 原有设计与优化设计的固有频率对比Table 14 Comparison of natural frequencies of the original and optimized designs