基于微惯性传感器的高灵敏度随动控制技术

张天， 靳舒馨， 王强， 段晓波， 刘铁成， 牛海涛， 侯曾， 杨毅， 刘彤

(1.中国兵器工业计算机应用技术研究所， 北京 100089； 2.北京卫星导航中心， 北京 100094； 3.北京理工大学 自动化学院， 北京 100081)

0 引言

随着现代军事装备的智能化升级，武器装备对感知认知与智能控制提出了更高需求[1-2]。随动装备作为一种典型的智能化装备，通过多种技术手段把受控对象与操控人员的肢体动作直接结合，实现自然的人机交互方式，提升作战效率[3]。在随动控制装备中，人员头部运动由惯性传感器、光电系统采集，经融合解算得到人员头部相对载具舱体的位置姿态变化量，生成控制信息[4]。该控制信息经载具控制总线传递给武器站、观察镜、雷达等执行设备，控制其跟随载具乘员头部实时准确运动[5]。随动控制系统的低延迟与高精度需求使得随动装备对信息采集到控制执行的实时性、准确性与稳定性有极强依赖[6]。

在大部分机电系统的设计中，因机电常数相对固定，精度指标与实时性指标通常难以兼顾，在机电系统对精度需求较高时，采取延长响应时间换取控制精度的方案；在实时性需求更高时，采用牺牲精度以缩短响应时间的方案[7-8]。不同的控制策略需要针对应用场景进行综合考虑。在随动控制系统中，随动精度与随动时延均为关键性指标，二者共同决定了随动控制装备的人机交互体验，需要机电系统即能满足实时性需求，又能满足精度指标。因此兼顾实时性与准确性的系统方案也成为了随动系统的设计难点。

目前低成本的随动控制方案通常采用微惯性器件[9-10]与光电系统配合完成测量，并将机电设备作为控制的最终执行器。对该系统而言，随动控制精度受到姿态采集精度与机电执行器精度的共同影响，随动控制的实时性受到姿态采集与解算延迟、机电控制与响应延迟的共同影响，需要进行针对性改进。

本文选取微惯性传感器与小型云台构成的随动系统作为研究对象，分别对实时姿态采集算法与云台控制方案进行设计，提升随动系统实时性与准确性。在姿态解算方面，本文选用低成本小型六轴微机电系统惯性测量单元(MEMS IMU)作为传感单元，通过姿态解算与互补滤波获取实时准确的姿态信息。在云台控制方面，本文使用模糊控制PID高频位置闭环算法改善现有双轴云台的机电控制系统，兼顾非线性输入下机电响应的实时性与准确性[11-12]。针对体感高动态随动系统的准确性与实时性指标，研究设计了姿态测量精度实验、头部运动测量实验与位置随动响应实验，进行了验证分析。

1 随动信息获取

以微惯性传感器为基础的微惯性测量技术是一种有效的低成本姿态测量手段。在姿态测量中，MEMS IMU输出为载体坐标系3个轴向的加速度(比力)与角速度信息[13]。需要通过姿态算法，根据上一时刻姿态信息与三轴陀螺仪输出，更新载体在导航坐标系下的姿态信息，完成随动信息获取。同时，考虑到惯性积分的累积误差，需要通过其他观测手段修正测量结果，提升姿态测量精度。

1.1 随动信息采集

考虑到传感器增重对人体头部造成的不适感，需要在合理体积质量下选型精度较高的MEMS惯性器件。综合比较下，本文选用六轴微机电惯性测量单元ADIS16475-2作为姿态测量传感器。该传感器常温漂移量小于5°/h、量程大于300°/s，接近战术级精度，且体积小、质量轻、功耗低，通过工装固定在头部不会产生不适感[14]。ADIS16475对外数据接口为SPI总线，最高采样频率为2 kHz，具备同步触发功能，可实现惯性数据的高频实时采集。使用DSP28335完成数据采集与解算，并通过串口实时发送至机电系统，如图1所示。

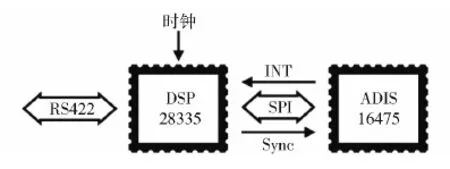
图1 搭载ADIS16475的DSP28335最小系统Fig.1 DSP28335 minimum system with ADIS16475

1.2 实时姿态更新

姿态解算将IMU的三轴角速度信息解算成头部姿态信息。推导姿态更新公式，三维空间中任意3个坐标系的角位置关系可通过3次姿态角基本旋转(欧拉旋转)或1次四元数旋转实现对齐，两种旋转方式的转换矩阵存在等价关系[15](见图2)。图2中，Oxnynzn为导航坐标系(东北天)，Oxbybzb载体坐标系中，yb轴向载体正前方，xb轴水平向右，zb轴与xb轴、yb轴呈右手螺旋准则，以滚动角γ、俯仰角θ、偏航角ψ表示3个姿态角。

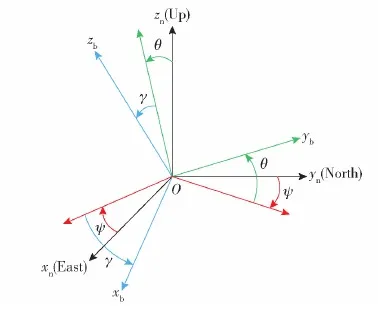
图2 坐标变换矩阵的3次变换Fig.2 Three transformations of the coordinate transformation matrix

(1)

基于四元数的坐标变换矩阵

(2)

式中：q0、q1、q2、q3为旋转四元数。

比照式(1)、式(2)可以求解姿态角

(3)

为实现四元数实时更新，还需要建立四元数微分方程：

(4)

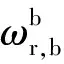
(5)

式中：ωx、ωy、ωz分别为IMU角速度测量值。由于MEMS IMU精度限制，本文中可近似忽略位置速率和地球自转速率对姿态角解算的影响。

由式(5)可见，在算法实际使用中，只要初始四元数已知，便可根据捷联惯导陀螺输出(采样间隔已知)实时更新四元数。

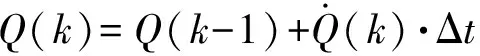
(6)

式中：k为离散采样序号；Δt为采样时间间隔。

更新四元数后，再通过式(3)求解姿态角，完成姿态解算。

1.3 互补滤波

由于陀螺仪误差会随着时间的增加不断积累，而加速度计不会随着时间的增加产生误差积累，尤其在低频状态测倾角会有理想的效果。利用这两种传感器在频域上的互补特性，设计互补滤波器融合两种传感器的数据，可以达到提高测量精度和系统的动态的目的。算法具体步骤实现如下：

1)将测量得到的加速度归一化，即

(7)

式中：ax、ay、az为IMU测量的加速度三轴分量。

2)通过姿态矩阵求解重力加速度由导航坐标系投影到载体坐标系的分量：

(8)

(9)

式中：δax、δay、δaz分别为三轴误差角。

4)利用PI控制环节求解陀螺仪漂移补偿向量：

(10)

(11)

式中：wx、wy、wz分别为陀螺原三轴漂移；x、y、z分别为三轴漂移补偿量；为修正后的三轴漂移；Kp、Ki分别为PI控制器的控制参数。

2) 跨移动平台适配能力，基于React Native，通过封装或引入基础组件形成基础组件库，实现“一次编写，分别编译，多端运行”的跨平台目标；

5)代入四元数更新方程式(6)中，求解角速度微分方程。

6)对四元数进行规范化处理，由式(3)求解姿态角的精确值。

根据应用场景不同，调整滤波器开启条件以及PI的控制参数可以有效抑制除航向角外的积分漂移。

按照上述算法，通过随动信息采集、姿态解算与互补滤波器3个环节完成控制器程序设计，可以准确获取人体头部姿态。此部分延迟主要存在于采集、解算与传输延迟，异步通讯延迟。经DSP内部时钟测量，该部分采集与传输总延迟相对于毫秒级的机电响应时间可以忽略不记。

2 云台控制设计

2.1 云台电气改造

在随动控制应用中，云台需要对外部控制命令做出准确且快速的响应，要求云台有较高的位置控制实时性与准确性[16]。但传统小型云台因转动惯量较大，电机驱动力矩不足，无法满足此应用的动态特性需求。同时，较大的驱动力矩会增大电机运动惯量，增大控制难度。需要根据机电控制对象设计电气方案来提升整体性能。

本文选用一种带有直流力矩电机、18位绝对位置编码器的小型云台进行算法改造，如图3所示。该云台可作为车载观察镜使用，并且云台的旋转部分体积与人体头部大致相当，选用其作为机电执行机构具有代表性。该云台外框绕方位轴z旋转，内框绕俯仰轴x旋转，外框轴系配有导电滑环，可连续无限旋转，内框轴系配置机械限位机构。云台内框轴系与外框轴系均采用高精密交叉滚子轴承，以保证该轴的回转精度和轴向承载及抗倾覆力矩。小型云台电气原理如图4所示。

图3 小型云台结构示意图Fig.3 Schematic diagram of the small turntable structure

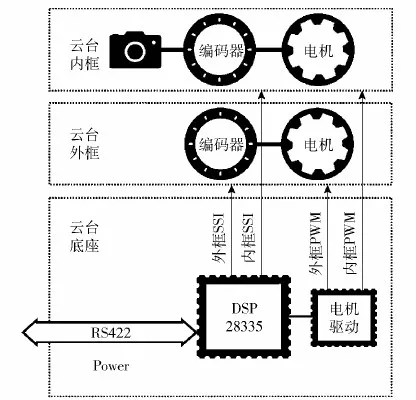
图4 小型云台电气原理图Fig.4 Electrical schematic diagram of the two-axis turntable

双轴云台的电气系统通过DSP实现编码器解码、电机控制功能。

1)编码器解码

编码器选用的18位绝对位置编码器，精度可达到±20″。在解码过程中，将DSP的两路多通道缓冲串行口(McBSP)设置为SPI模式，发送固定时钟信号至编码器，触发编码器返回编码信息。编码器返回的SSI二进制编码信息至DSP，完成数据接收过程。

2)电机控制

DSP通过异步串口(SCI)外设接收外部控制命令，并结合从编码器获取的云台位置信系解算出控制量(数字电压)。该控制量通过同步串口(SPI)发送，经DA转换为模拟信号发送至电机驱动器。电机驱动采用美国AMC公司的模块化驱动器以简化电气设计。该驱动器以开关速度快、压降小的IGBT功率模块构成双路四象限全桥电路，可根据±5 V以内的模拟电压生成PWM驱动电压，对电机进行驱动。采用成熟驱动模块作为电机驱动器，其成熟度高、可靠性好，降低了机电控制难度。

2.2 控制流程

本文使用高频位置闭环控制取代了速度闭环，用2 kHz的实时高频位置控制频率，具有更强的控制实时性，更适用于位置随动控制。云台的控制程序按照以下10个步骤进行(见图5)[17-18]：

步骤1系统、外设、中断初始化。

步骤2开启0.5 ms周期控制定时器。

步骤3使用DSP的McBSP收取编码器数据。

步骤4绝对位置编码器在0°与360°位置会发生位置跳变，进行圈数判断，以形成螺旋结构；从360°至0°时圈数加1(角度加360°)；从0°～360°时圈数减1(角度减360°)。

步骤5使用FIR滤波器对角度值滤波后储存，以减少角度测量的噪声干扰或台阶突跳。

步骤6从寄存器(缓存RS422中断数据)读取上位机发出的目标位置，因控制频率高于目标位置发送频率，若目标位置未更新则按照寄存器现有数值进行后续计算。

步骤7对角度值进行窗口采样后计算角速度值，以减少速度值的噪声，然后根据实际位置、目标位置计算角度偏差量、速度偏差量。

步骤8由模糊PID控制器根据角度偏差量以及速度偏差量生成Kp、Ki、Kd取值。

步骤9由Kp、Ki、Kd角度偏差量以及速度偏差量生成控制电压V，并进行饱和控制。

步骤10清空寄存器，进入下个控制循环。

在控制流程中，步骤6保证了云台能够在0.5 ms内收到位置指令。步骤8、步骤9决定了控制的稳定性、准确性、快速性。考虑到本文系统动静态要求，系统采用带有模糊PID控制的复合控制策略提升系统性能。

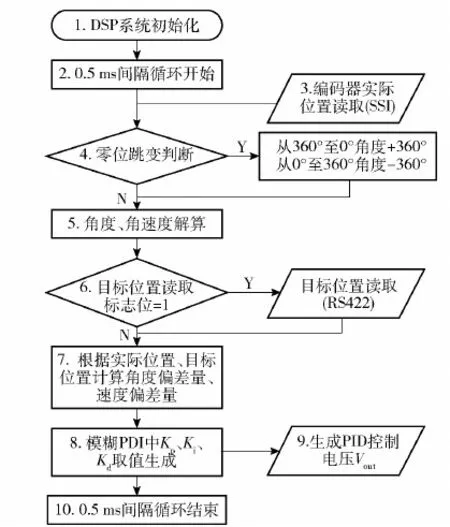
图5 以DSP28335为处理器的小型云台控制框图Fig.5 Control block diagram of the turntable with DSP28335

2.3 模糊PID控制

数字PID控制器通过微分增益提供系统稳定所需的阻尼，积分增益来消除稳态误差，速度前馈增益来减少阻尼引起的跟随误差(该项误差与速度呈正比)，如图6所示。图6中，Kvff为速度前馈增益，En为第n个采样时刻的位置偏差，P、I、D分别为为比例项、积分项、微分项产生的控制电压，S为累积误差。

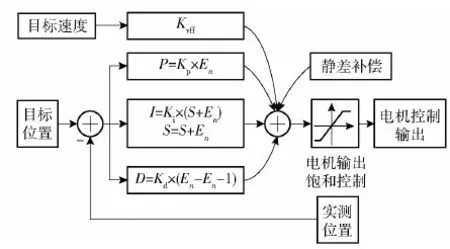
图6 数字PID控制器设计Fig.6 Design of the digital PID controller

数字PID控制器输出计算公式为

En=Pt，n-Pa，n

(12)

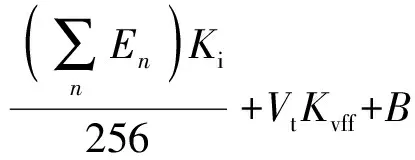
(13)

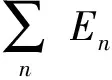
为提升高动态输入下机电系统的控制效率，采用模糊PID自整定控制，使控制器能够根据位置偏差En和速度Va调整Kp、Ki、Kd取值，以达到最优控制[19]。本文中响应时间与执行精度是重点关注指标，考虑到系统在目标位置距离不同时，应采用不同的PID控制参数，传统PID控制难以胜任，因此需要设计模糊控制器，按照不同阶段机电运动特性对PID取值进行优化[20]。

除上述控制策略外，约定云台的极限位置精度，以避免云台在目标位置的微小抖动。该现象是由于云台运动到目标位置后存在微小误差，此微小偏差经控制算法产生的驱动力矩已经小于云台轴系的静摩擦力，转台虽然不再运动，但此时控制器PID的积分项仍缓慢累积，直到再次驱动转台。当云台再次运动时云台内部静摩擦变为滑动摩擦，摩擦力瞬间减小，同时控制策略产生的制动力将云台制动，直至云台运动停止。该过程不断重复，形成云台在目标位置的微小抖动现象。因此，考虑到本文研究随动控制的精度极限，设定云台运行偏差在±0.01°以内时不再进行积分输出，以消除该稳态微小抖动现象，增强了控制稳定性。

3 实验验证

为了对基于微惯性器件与模糊控制云台的随动系统控制实时性与准确性进行验证，设计三部分实验内容。首先设计姿态测量精度实验，使用高精度双轴转台对惯性器件的短时测量精度进行验证，验证随动系统的姿态测量精度。随后设计头部运动测量实验，利用姿态测量精度实验中的姿态测量系统对人体头部运动进行测量，获取人体头部运动的典型参数。最后结合头部运动测量实验中的人体头部运动典型参数，设计位置随动控制实验，对微惯性器件与模糊控制云台随动系统性能进行综合表征，验证随动系统的实时性与准确性。

3.1 姿态测量精度实验

首先进行姿态测量精度实验，以验证IMU姿态解算得准确性。在姿态测量精度验证实验中将IMU与红外全局相机固定在902E-1型高精度双轴转台上，如图7所示。

图7 姿态精度实验设备图Fig.7 Attitude accuracy test equipment

在测试开始前对IMU进行30 min的上电初始化，使IMU达到恒定温度以减小零偏变化。在实验过程中锁定双轴转台的俯仰轴，使转台航向角从0°起，每次递增10°并保持30 s直至40°，再依次递减至0°。在运动过程中，采集计算机分别以10 Hz记录转台航向角信息，以1 kHz获取DSP解算的姿态测量信息，分别对采集到得转台真值与IMU测量数据标记时间戳，以便于后续数据处理。

数据采集后将数据对比如图8所示，从中可以看出与转台实际读取数据比较，IMU姿态测量结果基本准确。选取转台航向角40°与返程时航向角10°两个典型位置放大分析，发现IMU解算结果存在0.2°以内的测量误差。

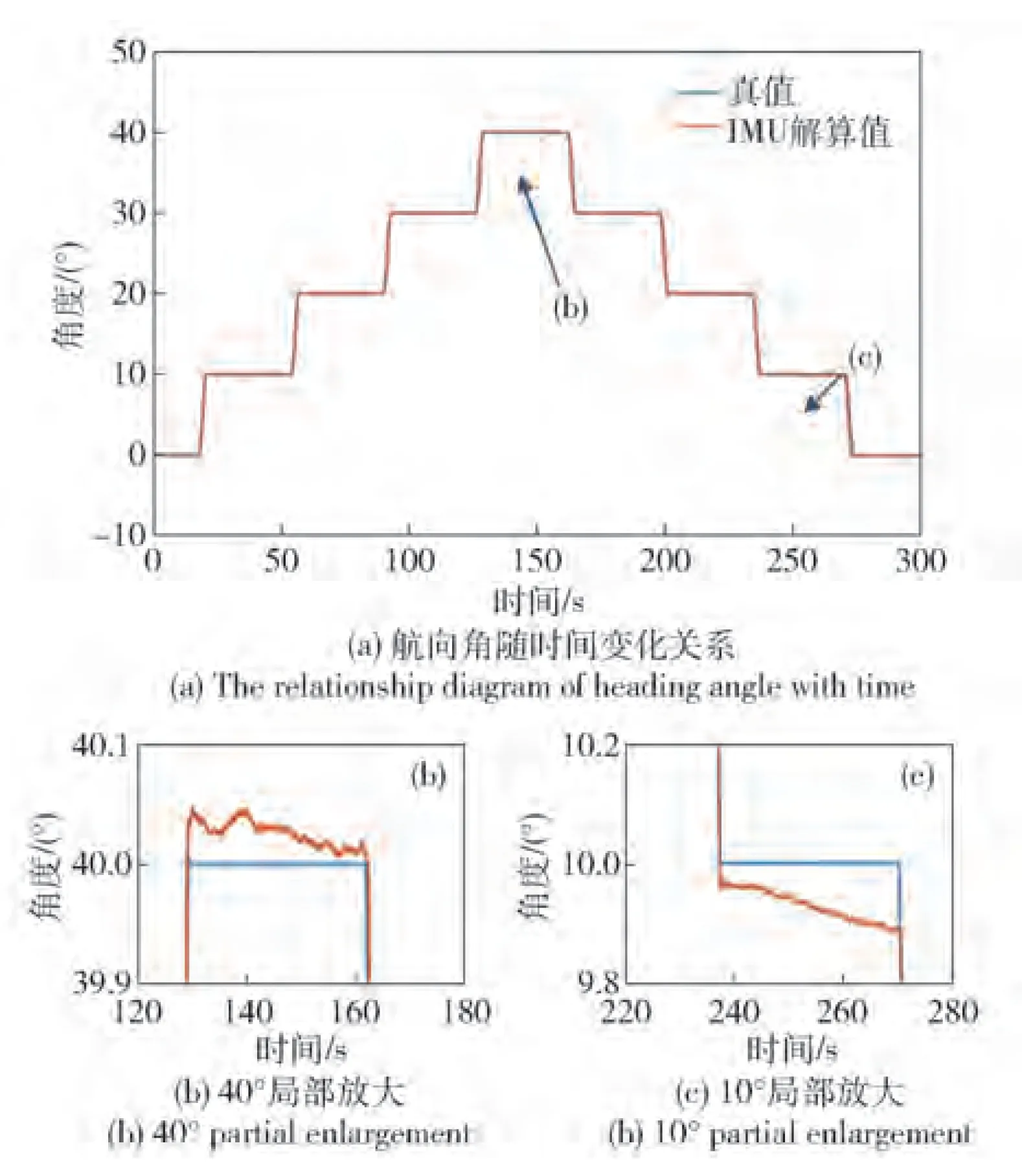
图8 姿态测量精度实验Fig.8 Attitude measurement accuracy experiment

为更清晰地观察IMU解算数据与真值相比的误差，将IMU解算值与真值作差绘制误差随时间变化图，如图9所示。总体上看，因测量时间较短，陀螺零偏影响可忽略。在实验过程300 s内，IMU解算精度较高，均方根误差(RMSE)为0.065 2°，可以满足短时姿态测量精度需求。误差主要原因在于转台运动状态下由于真值采样频率较低，且转台内部采集存在时间延迟波动，影响了运动状态下求得误差的精确度。

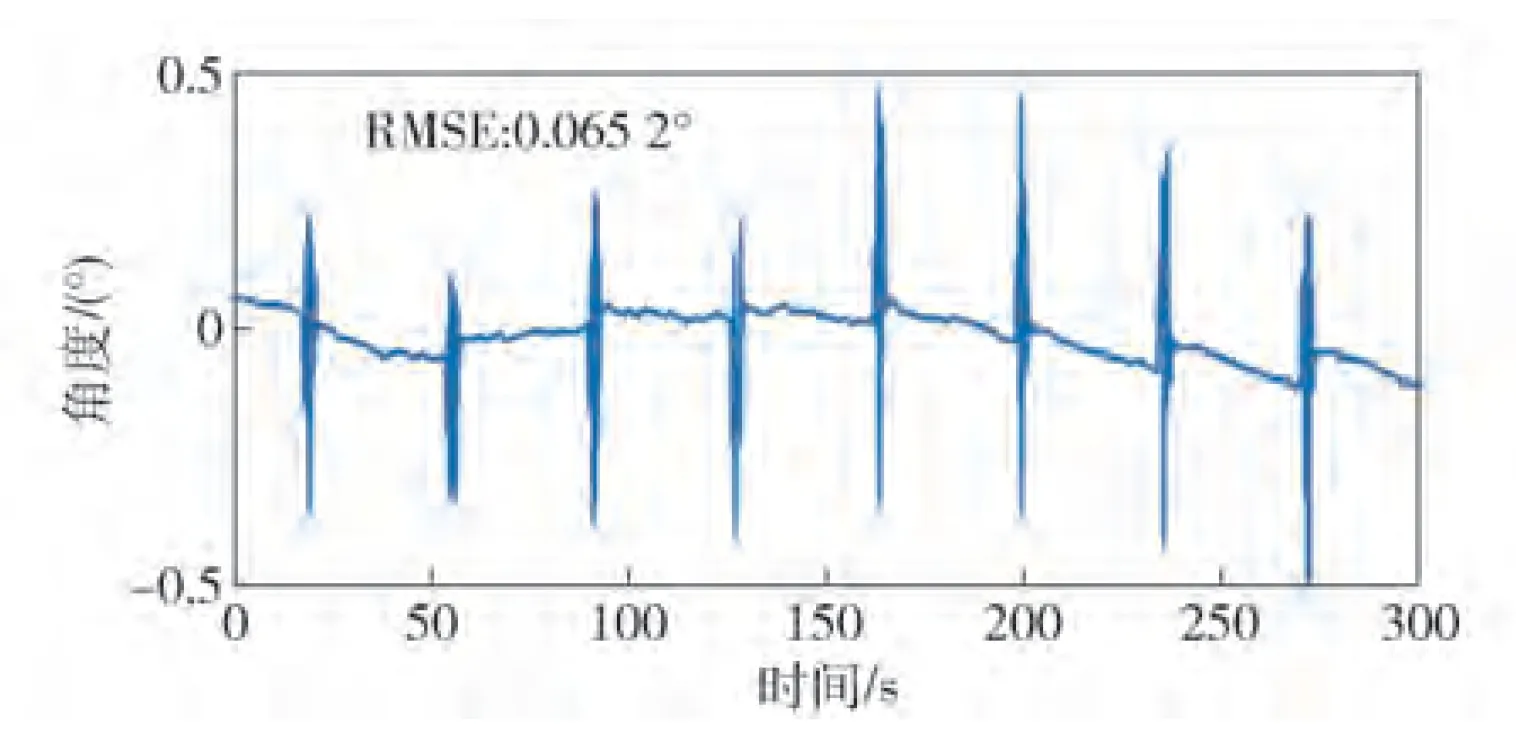
图9 姿态测量精度实验航向角误差随时间变化关系Fig.9 Relationship between heading angle error andtime

3.2 头部运动测量实验

将IMU固定在人的前额上，如图10所示。使用实时姿态更新与互补滤波算法获取头部运动姿态的角度信息。设计头部运动测量实验以模拟头部对外部阶跃信号的姿态响应，获取头部转动时的静态信息。在实验中，测试者头部从起始位置依次快速转头到A、B、C、D、E5个位置，并在每个位置停留一小段时间，如图11所示。为避免超出人体转动范围，A、B、C、D、E5个位置交错分布在正前方±60°范围内。该测试重复10次，测得数据如图12所示。

图10 头部运动测量实验设备Fig.10 Head movement measurement equipment

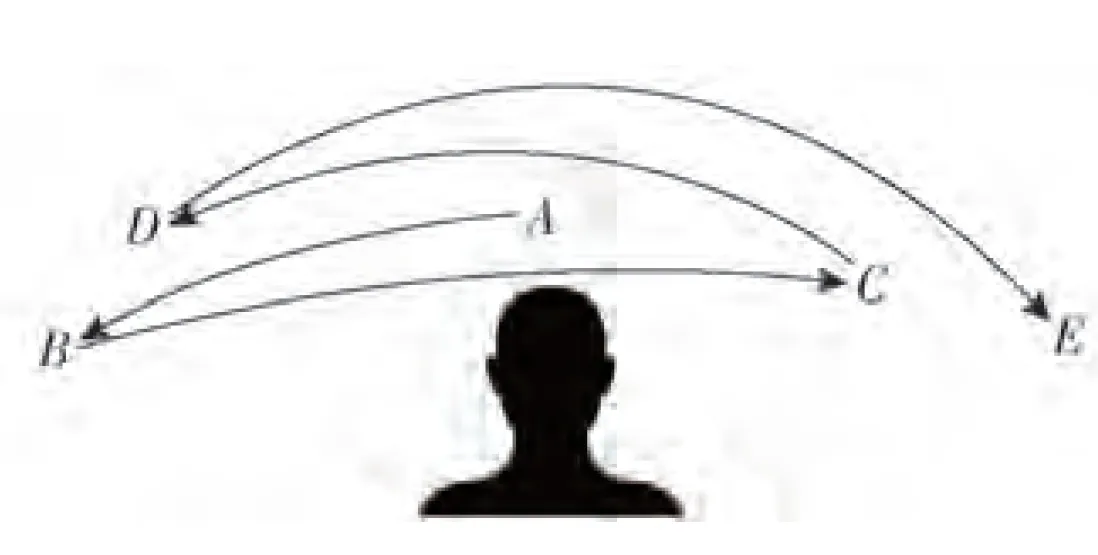
图11 头部位置测量实验运动示意图Fig.11 Schematic diagram of the head position measurement test

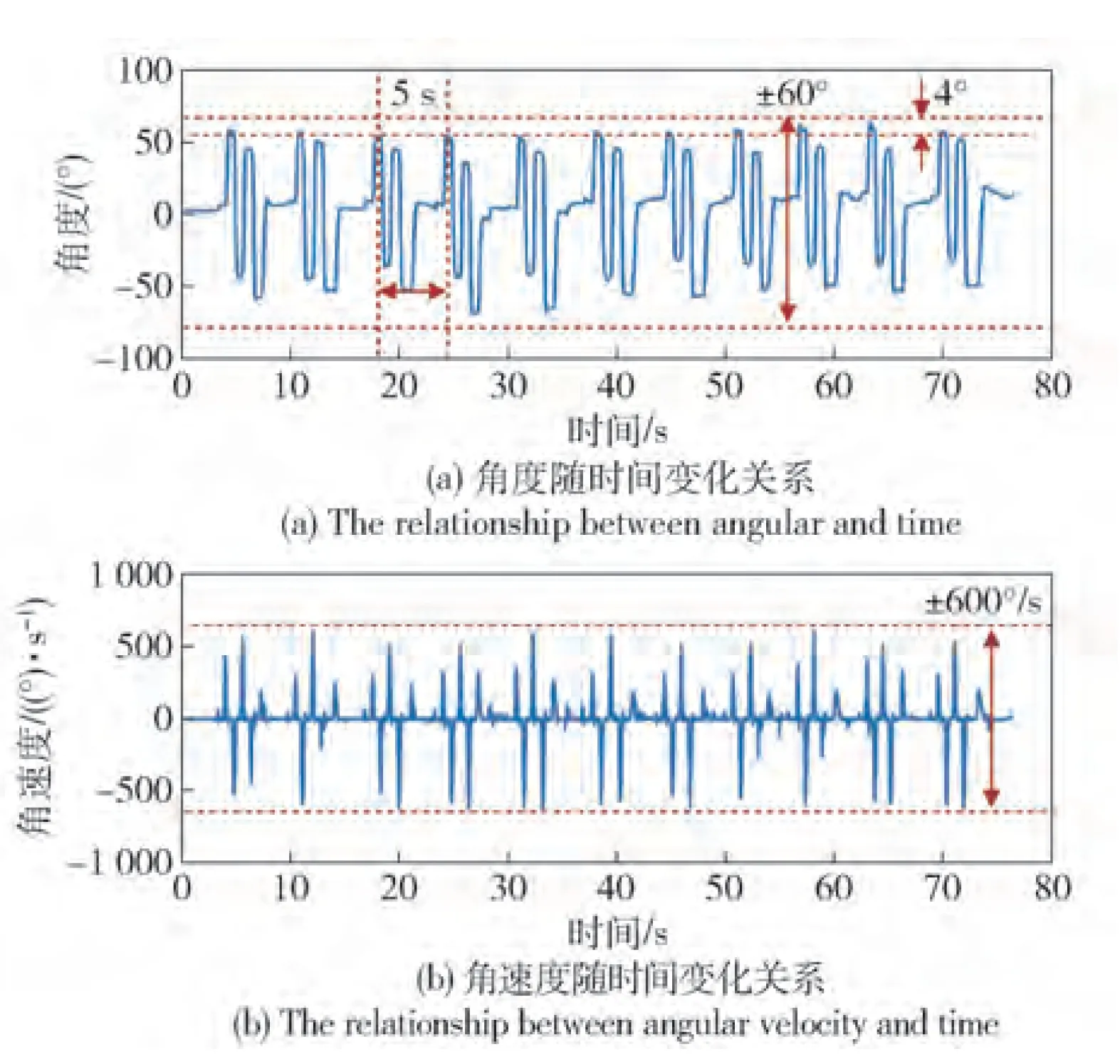
图12 头部位置测量实验10次测量数据Fig.12 Data of the ten measurement experiments

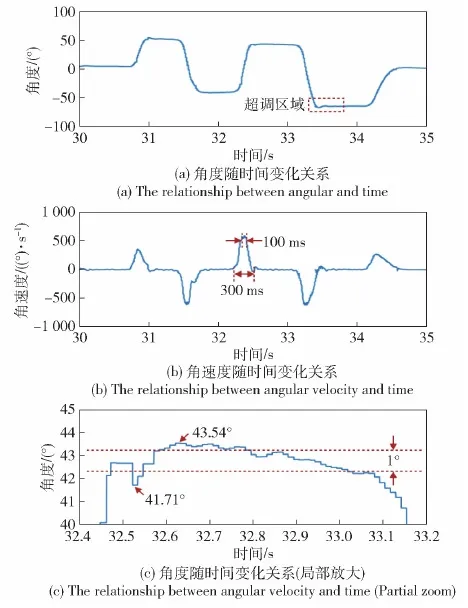
图13 头部位置测量实验单次测量数据Fig.13 Single-time measurement data

由10次测试数据可以看出，头部运动周期约为5 s左右，运动范围在±60°范围内，与位置点分布间隔相同。因眼部运动影响，多次运动中头部再次到达固定位置时存在位置偏差，该偏差在4°以内。虽然不同次测量的重复精度有限，但角度变化趋势大体相同，通过差分计算得到头部角速度极限值接近600°/s。

就单次测试数据来看，如图13所示，头部对单点阶跃信号的运动响应更近似多阶系统，体现在头部在到达指定位置点时，测得角度存在小幅超调。相邻点之间头部运动时间约为300 ms，因生理结构限制，极限角速度持续时间十分短暂，仅为100 ms左右。另外，从静止时的数据可以看出，即使在头部稳定时，姿态输出也有一定范围的波动，选取32.5～33.1 s这一段稳定时间观察角度变化范围，其中角度输出最大值43.54°，最小值41.71°，角度变化范围在1.83°以内，RMSE为0.51°。可以看出姿态输出波动范围高于“姿态测量精度实验”中IMU测量精度(RMSE为0.065 2°)一个数量级，其余头部稳定时的姿态输出也基本遵循这一精度特征。可以近似选取1°作为高动态体感随动控制的精度设计指标。

由人体头部运动的角速度与角加速度实测结果人可以看出，人体头部运动的极限角速度与角加速度很高，但维持时间较短，在设计随动机电系统时可根据此数据提出响应特性需求，并且为减少机电系统延迟，应尽可能匹配头部运动的角速度与角加速度指标。

3.3 位置随动响应实验

为验证整套体感随动系统运行精度与延迟情况，设计两个小型双轴云台的运动响应实验。在实验过程中，手动控制搭载IMU的1号传感器云台运动作为随动控制输入，解算的姿态数据作为随动控制命令发给2号执行器云台，并由2号云台执行运动。在运行过程中使用上位机同时记录1号云台与2号云台的角度数据，实验原理如图14所示。

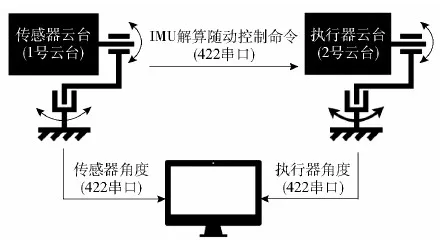
图14 云台运动响应实验原理图Fig.14 Schematic diagram of the gimbal motion response experiment

测量过程中两个云台姿态数据直接从云台内部的18位光电编码器获取，编码器角度测量精度优于0.005°，可近似认为该测量值为真值。2号云台已采用模糊PID控制方法，根据机电系统做出了最优化控制参数已设计，以保证随动控制的最快响应与执行精度。此外，为减小数据采集延迟带来的干扰，两个云台角度均通过同样的软硬件采集，传输至上位机时打上时间戳。

云台运动响应的具体实验设备布置如图15所示。为便于后续随动控制的性能评估，首先进行系统传感器到执行的随动延迟时间估算。在估算过程中迭代计算延迟时间t，寻找使得1号云台与2号云台角度差的标准差最小值σ。将使σ最小的时间t作为估算的随动延迟时间，如图16所示。

图15 云台运动响应实验设备Fig.15 Experimental equipment for PTZ motion response

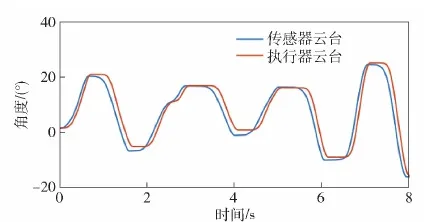
图16 随动响应延迟时间计算原理Fig.16 Schematic diagram for the calculation of follow-up response delay

实验过程中，为保证数据的准确性进行5组2 min以上测量，运动类型涵盖了低速运动、高速运动、往复运动、间歇运动等，因不同运动形式产生的随动效果存在一定差别，求得的多组随动延迟均值更具代表意义(见表1)。计算得到随动系统平均延迟为88.17 ms。延迟主要源自于云台机电系统执行过程中由转动惯量、转动阻尼等带来的响应延迟，这部分延迟难以通过算法改进来避免。

表1 随动延迟时间估算Table 1 Follow-up delay time estimation

为详细探讨随动精度与体感随动延迟之间关系，结合3.2节头部运动测量实验中人体头部的典型运动数据选取，考虑人员对目标视觉追踪、大范围目标切换、突然启动、突然停止等运动的极限工况，总结出了低速、间歇、大范围、高速、摇摆等典型运动形式，形成一组综合运动条件进行随动系统的精度特性分析。

采集一组综合运动条件下的数据进行比对分析。在实验中手动控制1号传感器云台在低速、间歇、高速、摇摆的混合运动中工作300 s，记录得到修正延迟后的1号云台与2号云台航向角随时间变化关系如图17(a)所示，并将高速运动部分与摇摆运动部分放大展示为图17(b)与图17(c)。1号云台与2号云台航向角差分求取的角速度随时间变化记录结果如图18所示。随动误差与时间关系记录结果如图19所示。

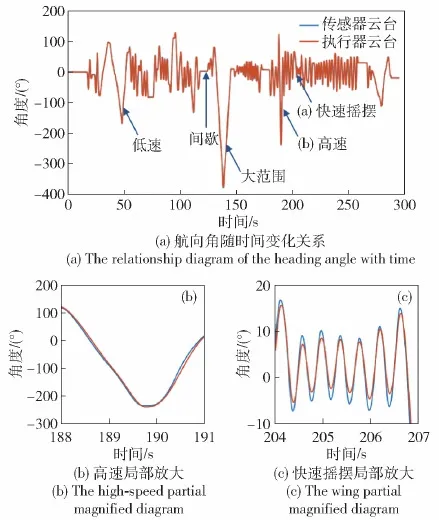
图17 位置随动响应实验Fig.17 Experiments of location follow-up response

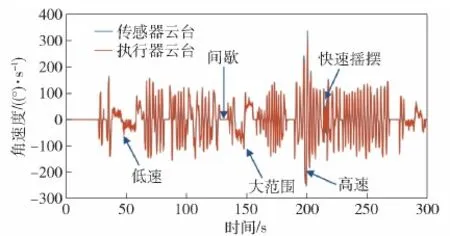
图18 航向角速度随时间变化Fig.18 Relationship between course angle velocity and time

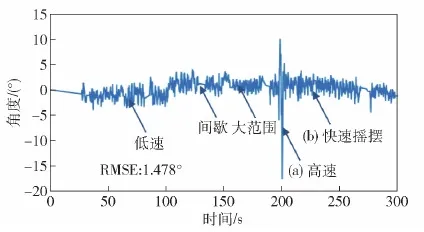
图19 航向角偏差随时间变化Fig.19 Relationship between course angle deviation and time

可以看出：1)在低速运动(速度峰均值约30°/s)情况下，随动控制效果较好，执行误差较小，即使运动范围较大也能保持较高执行精度；2)在间歇情况下，角度误差基本稳定在固定值不动；3)在高速运动(峰值约300°/s)状况下，执行云台以最大功率向目标位置运动，但受限于机电常数，运动过程无法达到目标速度，因此运动过程中角度偏差较大，运动结束后偏差得以快速消除，与位置跟随的控制逻辑相符；4)在快速摇摆(峰均值约50°/s)状态下，由于机电延迟，执行云台在未达到传感器最远运动位置时即收到了新的控制指令，开始返回，与机电控制逻辑相符。

总体上看，在实验过程300 s内，综合低速、间歇、大范围、高速、摇摆等运动形式，随动系统精度较高，能够在88.17 ms内实现RMSE 1.478°的随动运动精度，可以满足位置随动控制精度需求。该精度主要受限于机电控制环节，提升响应速度与精度一方面可以通过载荷、编码器、机械结构、线缆减重以降低转动惯量实现；另一方面，提升电机效率，能在单位转动惯量下实现更高功率输出，也能改善随动系统的机电特性。

4 结论

本文提出了一种基于微惯性器件与模糊控制云台的低延迟体感随动控制技术，通过低成本高采样频率的姿态算法与高实时性与响应精度的小型双轴云台模糊控制算法改进，实现了88.17 ms内实现RMSE 1.478°的随动控制。该随动控制系统能够满足无人机控制与观察、车载雷达与武器站控制等领域，可大幅降低设备操控复杂度，提升控制特性。后续优化一方面可围绕惯性系统滤波修正，引入观察量提升随动控制的长期稳定性；另一方面继续提升执行器机电性能，提升随动控制的响应速度与精度。