基于任务演化重要度的合成部队维修器材两级配置优化方法

吴巍屹， 贾云献， 史宪铭， 刘彬， 刘洁， 尹世庄， 朱曦

(陆军工程大学石家庄校区 装备指挥与管理系， 河北 石家庄 050003)

0 引言

合成部队是陆军转型建设的重要新生作战力量，所属装备型号繁多、结构复杂，同时现代战争的突发性、高机动性、高破坏性，致使装备维修保障难度增加。随着近年来实战化演习演训活动的增加，合成部队在遂行区域任务时需携行必备维修器材实施维修保障，由于任务空间的局限性，维修器材的合理配置将很大程度影响保障效果。

当前许多高新装备集多种功能于一体，组成结构复杂、部件逻辑关联度高。由于装备作战运用过程中在不同阶段对系统功能需求不同，导致在不同任务阶段下部件功能状态对装备系统功能状态的影响也存在较大差异。在制定维修器材携行方案时，应对不同任务阶段部件状态对装备系统功能的影响加以考虑，合理区分部件重要度，尽可能在满足任务空间局限性的同时充分考虑部件重要度这一影响因素，尽量避免因重要部件短缺而影响装备系统功能的正常发挥。

一直以来，对维修器材携行方案进行合理规划是装备维修保障领域的重点和难点问题。在维修器材的多级供应保障模型构建方面，1968年Sherbrooke[1]提出了经典MERTIC和VARI-MERTIC库存控制理论模型，该理论被广泛应用于各军种和地方领域，取得了很多工程实践，如航空装备、基地舰船、民机航材的备件保障系统优化[2-4]，之后很多学者在此基础上对MERTIC理论模型进行了优化改进。孙江生等[5]考虑了武器装备贵重备件修理与供应的现实需求，建立了三级修理供应体制下贵重备件库存保障模型，开展了面向多等级多层级保障系统的备件库存保障模型研究[6-7]。蔡芝明等[8]分析了备件需求的稳态与非稳态特点，建立了备件动态配置模型。在维修器材库存控制优化研究方面，赵建忠等[9]考虑备件质量、体积、费用任一约束建立器材配置单因素优化模型。也有部分学者综合多个因素、多种约束条件开展器材配置优化研究[10-13]，通过引入拉格朗日算子将多约束转化为单一约束，进行多约束条件下备件配置方法研究。

现有文献大多未考虑不同任务阶段部件重要度对备件配置的影响，文献[14-16]仅就备件关键性、重要度进行了专家定性描述或行业领域分类，对于部件重要度的评价不能依据实际任务阶段特点和装备功能需求给出定量描述。另外，合成部队尚属新生事物[17]，器材配置相关问题研究目前正处于初步阶段，仅在考虑遭敌打击情况下建立备件需求仿真模型和单级库存配置优化模型[18]上有相关研究，在两级器材保障运行机制下合成部队维修器材配置优化问题尚未见相关研究成果。

综上所述，本文针对不同任务阶段部件功能状态对装备系统功能状态影响程度不同的实际，研究建立装备部件的任务演化重要度模型，并以备件保障度为目标，构建考虑任务演化重要度的多约束条件下维修器材两级动态配置优化模型，通过算例分析验证模型的可行性。希望下一步可以为合成部队指挥员制定部队平时和战时器材配置方案提供一定的方法支撑。

1 合成部队两级器材保障运行机制分析

1.1 装备构成分析

合成部队可独立遂行作战任务，其装备构成是实施作战任务的主体和保证，主要包括装甲装备、火炮装备、防空装备等装备类型。装备通常具有多层次的结构特点，按照从高到低的次序，依次划分为装备、子系统、部件、元器件等。由于装备发展强调系列化、模块化，合成部队所属装备(这里以某型火箭炮为例)均可以分成底盘系统、火控系统、指控系统等多个子系统，各个子系统均是由多个部件构成，各部件之间的关系以可靠性连接关系进行描述，常见的连接关系有串联、并联、混连、表决系统等。综上所述，合成部队装备层次结构如图1所示。

1.2 两级器材保障运行机制分析

图1 合成部队装备结构层次Fig.1 Hierarchical diagram of equipment structure of synthetic force

装备维修作业体系是进行维修器材配置优化的基础。目前，随着装备的发展变化，装备维修由传统的三级维修作业体系逐步向两级维修作业体系转变[19]。不论是部队级维修还是基地级维修，都可看作是在两级维修保障系统下实施的维修保障。本文主要基于部队级维修构建两级维修器材保障模式，由本级和上级两级维修器材保障系统构成，其器材存储机构与修理机构相互对应，主要采取一个中心仓库对应多个本级仓库的两级层级结构。当装备可更换单元发生故障后在本级换件修理，若本级仓库有所需维修器材则立即更换到装备中，若没有则向上级中心仓库发出请领，上级中心仓库没有该种器材则应向基地级器材仓库请领或进行外部购置；换件修理后将故障件送至具有相应维修能力的修理机构，修复后在该级别仓库存储，若不能维修则组织报废。具体运行流程机制如图2所示。

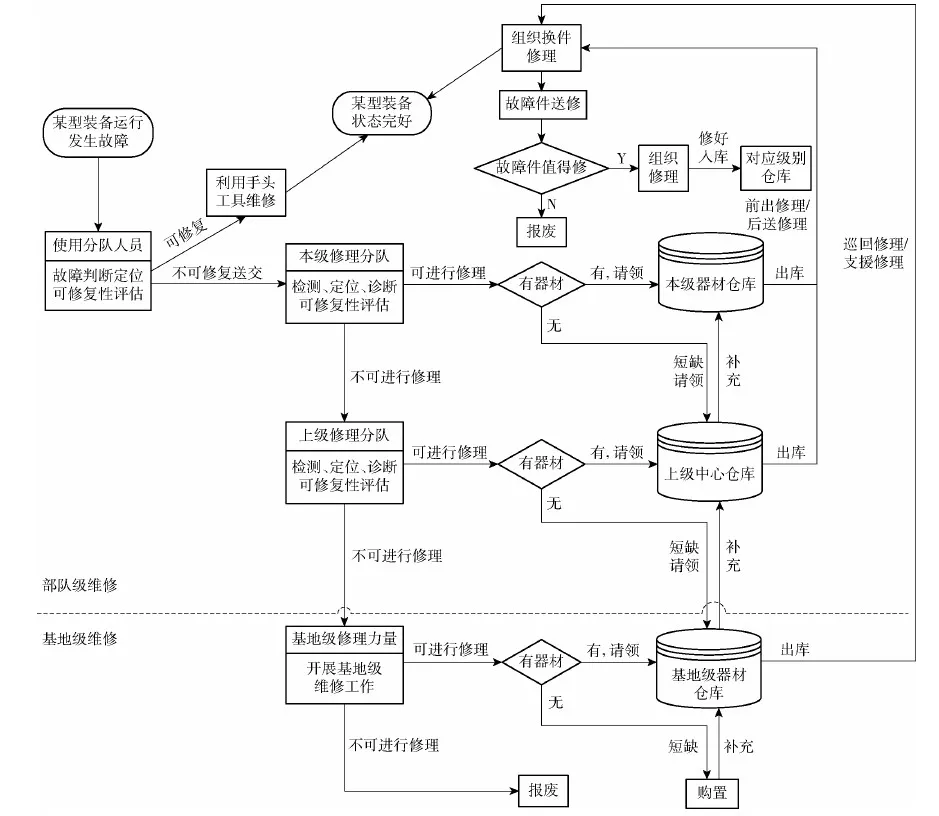
图2 合成部队两级维修保障系统运行流程Fig.2 Operation flow chart of two-echelon maintenance support system of the synthetic force

显然，在部队级维修作业体系下两级器材保障系统运行中维修器材的合理配置是一个关键性问题，对于有效实施维修保障、合理使用保障费用具有重要影响。

2 任务演化重要度模型分析

合成部队作为独立遂行作战任务的作战单位，其任务的顺利达成需要不同作战阶段各作战单元子系统之间相互配合。由于装备系统在不同阶段下任务剖面不尽相同，所要求实现的功能需求也有所不同，各个部件的重要度对于装备系统也有差异。

部件重要度是指部件的功能状态对装备系统功能状态的影响程度[20]；任务演化重要度是指综合考虑装备系统作战运用过程中不同任务阶段下部件功能状态对装备系统功能状态的影响程度，可以用来发现系统薄弱环节，为提升装备任务可靠性、优化器材配置提供依据。

随着科学技术的发展，装备结构发展经历了从简单到复杂、再由复杂到简单的进化过程，特别是高新、复杂装备在高可靠性要求之下，对装备的结构要求越简单越好，从过去复杂拓扑结构演变为简单的串联、并联、混连结构，以提高单元间相互独立性，并降低部件的关联性[21]。由于不同任务阶段装备主要工作子系统完成功能的时序关系、安装数目以及最小工作部件数均有不同，装备部件的任务演化重要度可以通过不同任务阶段下装备系统可靠性框图进行物理描述，如图3所示。因此，需要结合实际任务阶段情况分析部件功能状态对装备系统功能状态的影响，进而探索装备部件的任务演化重要度规律。

图3 不同任务阶段下装备可靠性框图Fig.3 Schematic diagram of equipment structure under different tasks

假设系统与部件具有故障和工作两个状态，其中状态0表示故障，状态1表示正常，且部件之间相互独立，

系统正常状态发生的概率为

P[X(t)=1]=R(t)E[X(t)]=0×P[X(t)=0]+1×P[X(t)=1]=P[X(t)=1]=R(t)

式中：R(t)为t时刻系统的可靠度；E[X(t)]为X(t)的数学期望。

系统正常状态下的结构函数为

Φ(X(t)=1)=Φ(x1(t)=1,x2(t)=1,…,xn(t)=1)P(系统正常)=R(t)=E[Φ(X(t))]=P[Φ(X(t))=1]

式中：xi(t)表示装备在不同任务阶段时系统组成结构所涉及的各个部件i在t时刻的状态。由于部件之间多以串联、并联、混连关系表示系统的组成结构关系，这里假设：

串联关系为

并联关系为

式中：n为系统组成结构所涉及的所有部件总数；Pi1(t)为t时刻部件i的可靠度；R(t)为t时刻系统的可靠度。

二态系统各部件的任务演化重要度描述了部件可靠性变化对系统可靠性变化的影响程度，用Ii(t)表示，

(1)

由于装备在不同任务阶段剖面下的组成结构不是一成不变的，单纯的串联、并联过于简单，本文重点以混连结构见图3(c)进行研究，分析部件的任务演化重要度与系统组成结构的依存关系。

1)系统的结构函数为

φ(X(t))= min {X1(t),X2(t),max {X3(t),X4(t)},X5(t)}

则系统可靠度表达式为

R(t)=P11(t)·P21(t)· [1-(1-P31(t))·(1-P41(t))]·P51(t)

2)计算各部件的任务演化重要度Ii(t)

参照式(1)求导计算，以部件1为例，可以得到部件1在此任务阶段下的任务演化重要度I1(t)：

I1(t)=P21(t)P51(t)(P31(t)+P41(t)-P31(t)P41(t))

式中：Pi1(t)可根据装备在研制、定型和使用阶段获得的详细可靠性数据得到。同理，可依次得出各部件任务演化重要度Ii(t)的排序，为下一步进行器材配置考虑部件的任务演化重要度这一重要因素奠定基础。

3 基于备件保障度的两级维修器材配置优化模型

通过分析合成部队两级器材保障运行机制，为提高整体保障效能，应当从系统角度考虑两级维修器材的配置与优化问题，实现在有限维修保障资源条件下保证装备的战备完好性和任务成功率。

3.1 两级器材保障系统构成

为便于系统建模，下面着重讨论部队级两级维修器材保障系统装备可修部件处理流向简化模型如图4所示。

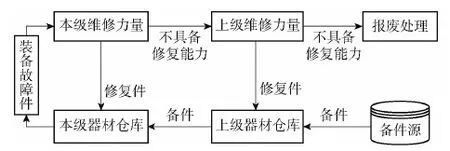
图4 可修部件处理流向简图Fig.4 Flow diagram of repairable parts handling

部队级两级器材保障系统由两级维修机构、两级器材仓库、购置备件源及备件的报废处理等要素组成。损坏装备作为维修保障系统的保障对象产生对器材的需求，两级维修机构负责对故障件的修理或报废。

3.2 备件保障度模型

为较准确地评价器材保障效果，解决好现有器材保障条件下最大保证装备正常工作的现实问题，可采用“装备平均工作时间、使用可用度、装备完好率”等评价部队训练、战备工作活动的指标来衡量器材配置效果，这类指标与器材的配置数量、备件延误时间、平均维修时间紧密相关。通过分析两级器材保障系统的运行过程，在不考虑其他影响装备停机情况如维修时间长、等待维修人员、维修机工具等因素且故障件维修存在一定报废率的情况下，备件供应延误主要取决于备件周转延误以及库存短缺[22]，若器材配置合理，库存较为充足，则通过“备件周转”可以消除这一问题。因此，仅从备件保障的角度来看，备件延误一定程度上会影响装备使用可用度，为较准确地刻画这一影响，本文定义了备件保障度并给出基于备件保障度的两级维修器材动态配置模型，旨在分析备件保障度对于装备使用可用度的变化影响，为较好地解决维修器材配置优化问题提供参考指标。

1)定义

备件保障度As：装备在规定条件下，可用时间与可用时间和备件延误时间之和的比值。

(2)

式中：MUT为装备平均可用时间；Ts为装备平均备件供应延迟时间。

2)备件保障度与装备使用可用度的关系

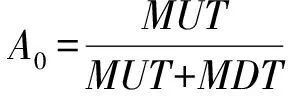
式中：A0为装备使用可用度；MDT为装备平均不能工作的时间；MDT′为除去备件延迟时间以外的其他总停机时间比如维修时间、等待维修人员、维修机工具等时间，

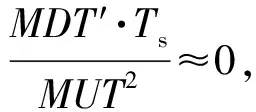
(3)

参考文献[23]中系统可用度分析中定义装备的固有可用度表示为

A′0在只考虑修复性维修时为装备的固有可用度；在综合考虑修复性和预防性维修时为装备的可达可用度，该值与装备先天的固有可靠性和维修性有关，后期可通过不断系统设计与改进予以检验完善。为简化计算，这里约定A′0为一常数，式(3)转化为

可以看出A0与备件保障度As为线性相关关系，因此，装备使用可用度A0在一定意义上可通过提高备件保障度As得到提升。

3.3 两级可修器材库存配置优化模型

3.3.1 模型假设

部队在遂行实际作战任务期间，由于本级维修能力有限，通常以换件修理为主要方式，即采用备件对故障件进行更换；若装备因重要功能部件发生短缺，则装备无法完成规定的任务。为方便建模，本文作如下条件假设：

①上级维修力量负责K个本级装备维修和器材供应保障，第i个(i=1，…，K)本级维修力量负责第j种装备共计μij台装备的维修和器材供应；

②器材的需求为泊松过程；

③装备换件维修时间可忽略不计；

④不同类别可更换单元对备件的需求相互独立；不考虑本级器材保障系统之间的横向调剂；器材保障系统处于稳态。

3.3.2 基于备件保障度的两级维修器材配置模型

本文在文献[23]维修资源的确定与优化中维修器材数量确定的基础上，构建了基于备件保障度的两级维修器材配置模型。

1)上级器材库存缺货数的计算

上级器材仓库得到备件的平均时间tl内库存需求量Yj(j为某型装备上第j类可更换单元(j=1,2,3,…,n))的概率密度函数为

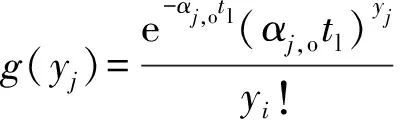
(4)

式中：yj为第j类可更换单元在一定时间内需上级仓库供应的备件数量；αj,o表示上级器材仓库备件需求率，

αj,o=∑∑αij(1-rij)tl=φjtc+(1-φj)td

αij为第i个本级维修保障机构所保障的某型装备中第j类可更换单元对备件的需求率，rij为本级修理率，即第i个本级修理机构能够修理第j类故障件的数目占第j类故障件总数的比率，φj为第j类故障单元的报废率，td和tc分别表示平均上级修复时间和平均上级购置时间。

因此，在tl内上级器材仓库库存水平为So,j时缺货数Di(So, j)的期望值为

(5)

2)本级器材库存得到备件时间Tj的确定

令ηj表示上级库存缺货率，即在tl内上级仓库库存的平均缺货数与需求数的比率，有

则本级器材仓库得到备件的平均时间Tj为

Tj=rijtb+(1-rij)[to(1-ηj)+(to+tl)ηj]=rijtb+(1-rij)[to+ηjtl]

(6)

式中：tb为平均本级修复时间；to为平均本级请领周转时间。

3)本级器材库存短缺数的计算

与式(5)的计算思路相同，可得到在Tj内本级器材仓库库存水平为Sj时，本级器材仓库备件期望短缺数E[Bi(So,j,Sj)]为

(7)

(8)

式中：xj表示本级器材仓库在Tj内对第j类可更换单元的备件需求量。

4)备件保障度的计算

设ξi表示本级器材仓库库存缺货率，则

对于给定任务时间t内，每一个第j类可更换单元(假设每个装备上有j类单元qj个)，由于缺少备件造成的装备停机时间为

每一个第j类单元的备件保障度为

(9)

对于本级维修任务中，每型装备的第j类可更换单元的备件保障度Aj为

整个装备的备件保障度As为

(10)

第i类装备的使用可用度Aoi为

Aoi=A′o·As

(11)

式中：A′o为装备的固有可用度。

合成部队多型号装备群的使用可用度A为

(12)

式中：N为装备类型总数；αi为合成部队不同型号装备对于整个装备系统体系的贡献率，其权重值可由专家打分法确定，且∑αi=1。

4 优化模型及算法

4.1 考虑任务演化重要度的器材配置优化模型

装备使用可用度在保障资源不受限的条件下可随备件保障度的提高而满足指挥员不同目标要求。当部队遂行作战或演习驻训任务时则不能无限制地携行全部器材，必然受运输车存储空间、车载质量、保障费用等综合因素的制约。此外，部队应优先携行对装备系统功能状态影响较大的重要器材。因此本文在器材配置优化求解过程中，除考虑车载体积、车载质量、保障费用等基本约束条件外，将任务演化重要度纳入器材配置优化目标函数建模中。故两级维修器材配置优化模型为

(13)

式中：kj为第j个可更换单元的任务演化重要度；Vj为第j个可更换单元的体积；Mj为第j个可更换单元的质量；Cj为第j个可更换单元的费用；Vs为当前器材配置方案最大体积；Ms为当前器材配置方案最大质量约束；Cs为维修器材总费用约束。

4.2 模型求解

合成部队维修器材两级配置方案的目标函数是使装备的备件保障度最大，并突出重要部件备件保障度权重酌情增大的现实特点。本文针对多约束方程式(13)利用边际分析法[18]进行器材配置方案的优选。

边际分析法是METRIC、OPUS软件等核心算法，属于典型的贪婪算法，其核心思想是比较不同种器材在不同级别每增加一个器材的效益值增量ΔA/z(z为约束值，如费用、体积、质量等)，从而确定选择增加哪一类器材。边际分析法要求效益函数为凸函数，本文影响器材配置优化的因素为多个变量，必须将多个变量转化为单变量约束才能继续使用边际分析法，因此首先进行多约束变单处理，引入拉格朗日算子，将3个影响因素转换为复合约束zj，具体表示为

zj=λVVj+λmmj+λccj

(14)

式中：λV、λm、λc分别为体积、质量、费用在复合约束zj中的权重因子；Vj、mj、cj分别为第j类可更换单元的体积、质量和费用。根据实际情况可设置任一权重因子值为零，将多约束条件转化为单一约束；也可设置各个权重因子不为零，将其他因素等效转化为单一复合约束。此时，可将式(10)写为

(15)

令当前器材资源组合为Zj=(z1,z2,…,zj，…,zn)，在此基础上为第j类器材增加一个备件后器材资源组合为Z′j=(z1,z2,…,z′j,…,zn)，对式(15)等号两端取对数，可得

(16)

根据边际分析算法在每轮迭代过程中得到的收益(备件保障度增量)除以成本值(复合约束zj)，得到边际效应值δ：

(17)

通过式(17)分别计算出本级和上级器材仓库在每一轮迭代中每项器材增加的边际效应值δ，将最大值δ所对应的该级别库存该类器材数量加1，依此循环，直到满足所有指标约束后，算法结束。此时得到满足多约束条件下的最优两级维修器材配置方案为

(18)

4.3 约束因子初始化及调整更新

由于器材体积、质量、费用对模型优化影响不同，在进行优化计算之前，需要首先合理确定体积因子λv、质量因子λm、费用因子λc的初始值，分别记作λv0、λm0和λc0，其确定方法如下：

1)只考虑单一因素影响如只关注体积，不再考虑其他约束影响时，令λv=1，λm0=0，λc0=0，通过边际分析计算得到一组初始最优器材配置方案s0=(s1,s2,…,sj,…,sn)；

2)计算该器材配置方案s0下所对应的器材总体积、总质量和总费用V(s0)、M(s0)、C(s0)，并重新计算初始约束因子λm0、λc0，计算方法如下：

(19)

将式(19)代入式(14)，再次利用边际分析法进行迭代寻优，得到另一组器材配置方案s=(s1,s2,…,sj,…,sn)。若该方案所对应的器材总质量、总费用中任何一个约束超过设定指标，则需要增加该约束的权重因子值。其增量计算如下：

(20)

式中：Ms、Cs分别为设定的约束指标值。若得到的配置方案所对应的质量、费用仍然超过了设定的指标，则可以在当前约束指标权重基础上，通过式(20)对其数值动态调整。当然可能会出现一种特殊的情况，在既定的备件体积、质量和费用约束下无论怎样调整权重因子也不能得到一组满足所有约束条件的解，在此情况下就需要重新设定条件，可适当降低备件保障度目标指标或增加质量约束、体积约束指标。

3)同样也可根据指挥员经验，判断各个约束对于任务完成结果的影响程度来确定权重因子的判定规则，例如根据指挥员分析判断，各约束因子权重应满足以下规则：

λv≥λm≥λc

(21)

该判定规则反映出体积约束是指挥员认为限制本次任务顺利达成首要考虑的因素，质量、费用为次要因素。在优化计算过程中，若器材总体积V(s0)超过约束条件Vs，则需动态调整其他约束因子λm和λc。调整前首先比较当前权重因子是否符合指挥员的判定规则，只需对违反规则的权重因子进行调整。这里以λm0<λc0为例，仅需更新λm的计算，λc保持不变，此时令λm=Vsλm0/V(s0)，再利用边际分析法进行迭代寻优，得到另一组器材配置方案。

4.4 基于MA-OD目标分解的边际分析法算法设计

传统边际分析法通过反复迭代能够寻求满足目标的最优库存方案解，使得指挥员可依据设定指标对器材配置方案进行分析和选择，该算法简便直观，易于实现。但随着器材品种、保障体系多级库存机构数量的增多，维修器材的多级多约束配置优化就会演变为大规模、非线性NP难问题，模型算法的执行效率会大幅下降，以模型决策变量为m个站点i种器材的库存量集合矩阵Sm×n为例，采用传统边际分析法计算时需迭代的次数G=m∑nj∑si[24]。

为提高运算效率，有效解决数据规模空间急剧增长的实际问题，本文提出一种基于目标分解(MA-OD)的边际分析算法。该算法沿用分层优化的思想[9]对传统边际分析法进行分层改进，首先进行从装备使用可用度到部件平均可用度的分层折算，同时兼顾不同部件任务演化重要度不同的特点，将模型目标函数按重要度分解为不同种类的备件保障度目标描述以突出重要器材重点保障的原则；最后，通过迭代的过程完成所有类别器材的优化配置，该算法的预计迭代次数为N=m∑nj·si。具体求解步骤如下：

步骤1分层初始化。根据装备使用可用度指标Ao确定其所属的各项部件初始平均可用度A′oj：

(22)

步骤2按部件任务演化重要度分解目标备件保障度Aoj。按照式(10)可知装备的使用可用度和所属部件备件保障度线性相关，考虑各个部件重要度不同，要保证A≥Ao，各个部件的备件保障度可因任务演化重要度酌情调整，以此作为后续器材合理配置数量的目标依据。设Kj为第j个可更换单元的任务演化重要度，各个部件的目标备件保障度Aoj计算如下：

(23)

由于在相同任务阶段下部件任务演化重要度评价等级(重要、次重要、不重要)区别差距不大，即能保证A≥Ao。

步骤3采用边际分析法分别对各项部件进行优化计算，得到关于各项部件的目标- 约束曲线图。

步骤4拟合装备使用可用度曲线，验证各部件的目标备件保障度Aoj乘积：∏Aoj≥Ao，则算法结束，得到器材配置优化方案。具体流程如图5所示。

图5 MA-OD算法流程Fig.5 Algorithm flow of MA-OD

5 算例分析

5.1 任务想定

以某集团军对西部方向遂行封控作战演习任务为例，上级决定将合成1旅、合成2旅、合成3旅组成前沿作战群。按照上级命令，要求前沿作战群按时机动至集结地域，并满足部队装备使用可用度不低于95%的要求。为保障该部队装备完好性和任务成功率，需在运力受限条件下合理规划携行维修器材配置方案，使得该部队装备的使用可用度最大。已知3个合成旅部队编制、装备实力基本相当，主要以自我保障和上级保障两种方式实施装备维修保障，预计本级器材仓库平均请领周转时间为3 h，上级平均修复故障件时间为2 h，上级平均筹措器材时间为50 h，部队在战斗实施阶段时主要编配3种型号装备负责重点任务的达成，其装备主要系统可靠性框图如图6所示，相关参数见表1。假设部队在任务实施过程中装备损坏事件服从泊松过程，现以上述背景对该群进行军旅两级维修器材配置方案规划。

图6 战斗实施阶段下合成部队装备群构成Fig.6 Composition of the equipment group of the synthetic force during conduct of combat

5.2 解算流程

首先依据该任务阶段装备系统组成见图6，计算装备群在战斗实施阶段下各部件的任务演化重要度，计算方法见下述计算，得出所属装备各部件的重要度分值及排序如表2所示。

参照装备1系统可靠性框图计算各部件的任务演化重要度为

参照装备2系统可靠性框图计算各部件的任务演化重要度为

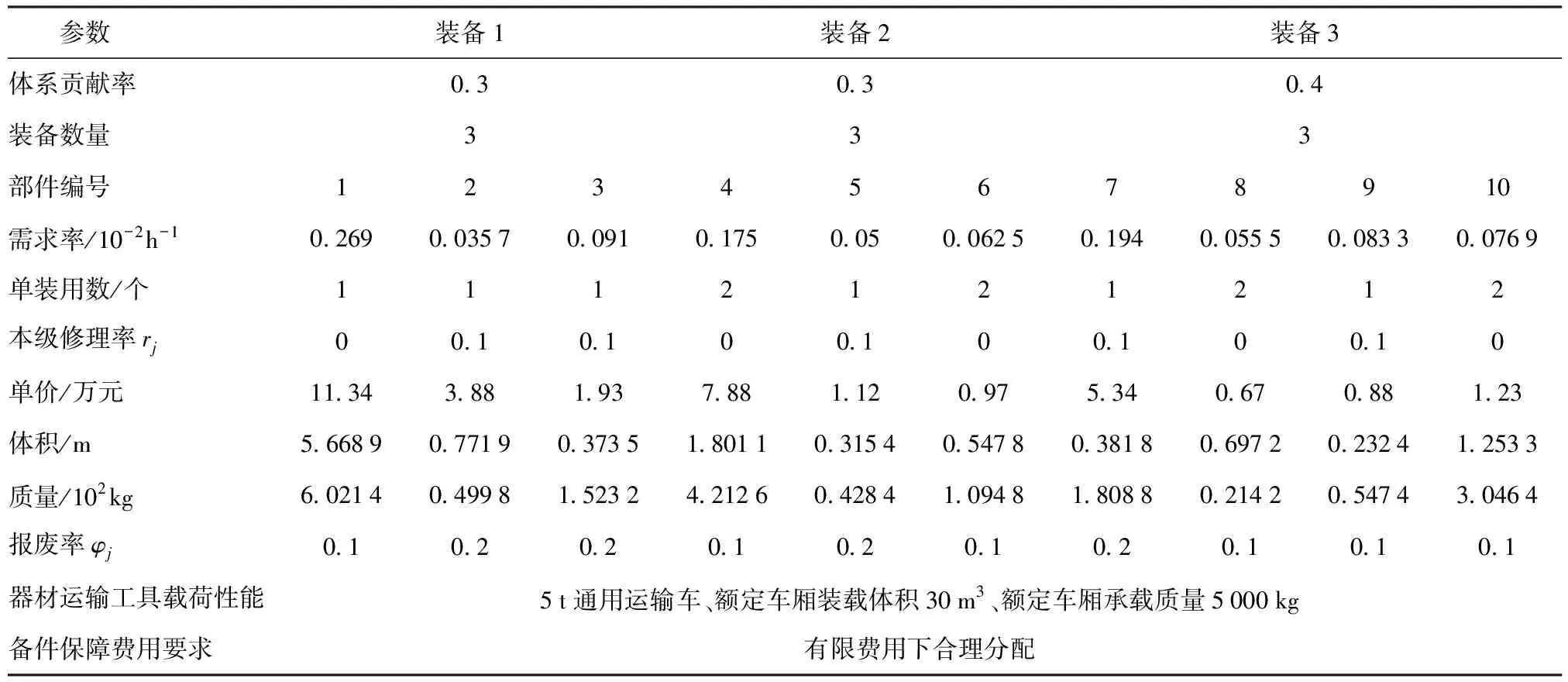
表1 所属部队装备相关参数Table 1 Equipment related parameters

表2 战斗实施任务下装备部件重要度分值Table 2 ScoringTable for the importance of equipment components under combat implementation tasks

参照装备3系统可靠性框图计算各部件的任务演化重要度为

本例采用第2种考虑装备体系贡献率的方式，对实际任务演化重要度打分和归一化处理；为满足指挥员对整个任务期间装备使用可用度要求不低于95%的目标，现结合部队实际运力载荷要求，分别以费用、体积、质量为约束，采用前文所述优化模型和算法求解满足要求的器材配置优化方案。

根据模型求解步骤，首先按照传统边际分析法只考虑单一约束如体积，确定初始约束因子，令λv=1，λc=λm=0，即不考虑器材其他约束时，通过优化计算得到一组携行器材配置方案s0(3，1，2；4，1，1；5，0，0，1)。在该方案下，装备使用可用度A(s0)为95.8%，器材费用C(s0)为103.3万元，器材体积V(s0)为29.755 m3，器材质量M(s0)为5 207.44 kg。使用该数据计算得到初始体积、质量约束因子值：

根据规定通用运输车体积约束指标30 m3，质量约束指标5 t，在仅考虑器材体积约束时，此配置方案s0不能满足运输车载荷要求。需引入初始约束因子λm0、λc0得到综合约束因子值zj，经迭代计算得出另一组器材携行配置方案s(3，1，1；4，1，1；4，1，1，1)，该方案下装备可用度为95.5%，器材费用为97.58万元，器材质量为4 950.4 kg，器材体积29.93 m3，该配置方案满足各项指标要求，因此方案s为最终优化配置方案。

5.3 结果分析

依据不同目标要求动态调整各约束因子值，可以实现不同目标、约束条件下最优两级器材配置方案见表3，具体方案结果和指标描述见表4，各配置方案目标- 约束迭代变化曲线如图7所示。

表3 多维目标- 约束下器材配置方案比较Table 3 Comparison of spare parts allocation schemes under different constraint conditions

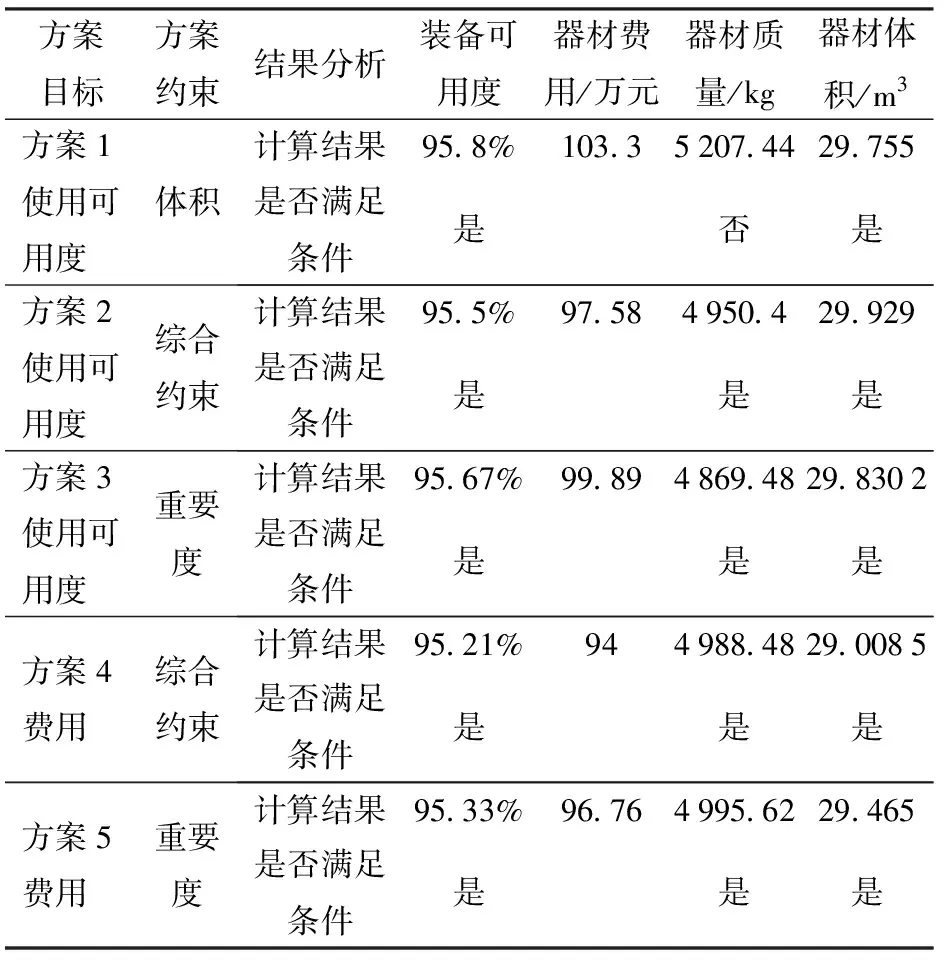
表4 多维目标- 约束下器材配置方案结果对比Table 4 Comparison of the results of spare parts allocation schemes under different constraints

图7 不同目标- 约束迭代曲线图Fig.7 Objective-constraint relationships under different constraint condition

根据表3所示的各类配置方案，可以从不同维度得出各方案所对应的装备使用可用度，具体结果见表4。对比分析各类配置方案可知：在5种方案中，当仅考虑单一约束进行方案求解时如体积方案1，所得方案不能满足所有约定条件；当考虑综合约束时所得方案符合要求，但因考虑目标、约束条件侧重角度不同，器材配置方案有所不同，所达成的目标效果也有所不同。具体分析如下：

1)分析各类方案可知：方案1为仅考虑单一体积约束得出的器材配置方案，相比而言体积较大的部件比同等条件下的其他部件配置量较少；方案2是考虑综合约束条件下的器材最优配置方案，各类器材配置数量普遍介于单一约束方案下的极值配置数量之间。这类方案不仅满足器材运力载荷要求，也可兼顾指挥员经验规则，通过动态调整各个约束权重因子值，最终得到满足指挥员基于任务成功影响决策偏好的军事目标方案；方案3是考虑部件任务演化重要度不同得出的器材配置方案，对于同等条件下故障率较高且较为重要的部件配置量相对增加，这种方案改变了传统可用度模型中将部件重要度同等对待的构建思路，在器材配置策略上可以做到重要器材重点保障，同时兼顾一般器材，装备使用可用度比未考虑重要度下综合约束配置方案有所提升；方案4与方案5是从费用管理的角度考虑综合约束和部件重要度的两类配置方案，与其他方案对比，这两类方案可以在满足约束条件的基础上有效降低器材配置费用，这对优化平时部队器材配置费效比也有一定的指导意义。

2)分析配置方案约束- 目标迭代曲线(见图7)，曲线上任意一点都描述了当前约束条件下的最优结果，这里以考虑单一约束—体积为例，当装备使用可用度达到其规定的指标95%时，器材总体积为28.95 m3，因此设定的器材体积约束指标必须满足Vs≥28.95 m3，如果Vs不能满足28.95 m3，就必须调整可用度指标，以通过降低可用度来满足体积约束条件。

3)通过对比分析两级库存器材配置方案可以发现：以备件保障度为目标的维修器材两级动态配置模型可有效降低因备件保障延误对装备使用可用度产生的风险影响。特别对于故障率高、本级修理率偏低且存在一定报废率的可修部件，在不考虑其他影响装备停机情况如维修时间长、等待维修人员、维修机工具等因素下，产生备件延误的关键因素在于上级器材库存得到备件的时间。因此，当作战部队规模较大时，两级维修器材动态配置模型能够有效缩短备件短缺延误时间从而提高装备使用可用度。从一定意义上来说，这种配置模式比较贴近现行军旅两级部队现实需求和装备维修保障实际，与战时军旅两级维修保障体系下维修保障任务区分、力量编组、资源配置的实际运行情况较为一致。因此，加强陆军合成部队维修器材两级配置优化研究对于降低器材保障不确定性、提升部队装备使用可用度和任务成功率具有一定的指导意义。

6 结论

本文以面向合成部队维修器材两级配置优化研究为背景，针对不同任务阶段部件功能状态对装备系统功能状态影响程度不同建立了装备部件的任务演化重要度模型，相比传统模型更加注重部件重要度的区分对待。以基于任务演化重要度的备件保障度为目标，构建了合成部队维修器材两级动态配置优化模型，通过引入拉格朗日算子求解出符合多约束条件的最优配置方案。最后以某合成部队遂行典型任务为例进行了算例验证。结果表明，本文构建的考虑任务演化重要度的两级维修器材配置模式在资源受限时特别是战时比较贴合部队现实需求和装备维修保障实际，该模式为陆军合成部队开展维修保障资源优化配置提供了新的理论指导，对于提高装备可用度和任务成功率具有一定的指导意义。