BP神经网络结合粒子群优化卡尔曼滤波的MEMS陀螺随机误差补偿方法

万芯炜， 王晶， 杨辉， 李毅， 张远再， 王路

(西南技术物理研究所， 四川 成都 610041)

收稿日期：2022-01-20

0 引言

导引头的稳定平台中，速率陀螺输出的角速率信号对于导引头视线角速度的解算至关重要。常见的速率陀螺主要有挠性陀螺、激光陀螺、光纤陀螺和微机电系统(MEMS)陀螺仪等。MEMS陀螺仪相比于传统的陀螺仪具有质量轻、体积小、价格低、功耗低、启动快、可靠性强、环境适应性强、易于集成等诸多优良特性，在低精度、低成本惯性系统中获得了越来越广泛的应用，同时也迎合了武器系统向低成本、小型化、便携化发展的趋势[1]。

但是由于制造工艺、材料和封装技术等的限制，MEMS陀螺存在误差相对较大的问题。MEMS陀螺仪的误差按其特性分为确定误差和随机误差两项：确定性误差属于系统误差，可以通过标定实验去除；随机误差又称为不确定性误差，表现为弱非线性、非平稳和慢时变，没有明确的规律且易受外部环境影响[2-3]。因此，减小MEMS陀螺仪随机误差，对MEMS陀螺精度的提高至关重要。受限于当前的材料以及加工工艺水平，通过改进加工工艺或使用新材料来减小MEMS陀螺误差十分困难。因而现有的减小MEMS陀螺误差的方法主要是进行滤波补偿，主要分为两类：一是不需要构建误差模型的补偿方法，主要有数字滤波、小波阈值降噪和经验模态分解等；二是先建立误差模型，再对该模型进行滤波补偿，误差建模常用的方法有Allan方差法、时间序列分析法和人工神经网络等[4]。

文献[5]提出了BP神经网络辅助卡尔曼滤波对陀螺仪数据进行降噪处理的方法，结果表明BP-卡尔曼滤波比卡尔曼滤波效果好。文献[6]提出将MEMS陀螺的输出和转台的实际转速作为样本，建立基于BP神经网络的补偿模型，在低转速区间上，神经网络的补偿效果比传统方法更好。国外学者Bhatt等[7]提出基于增强型支持向量机建立MEMS单元的误差模型，陀螺仪的噪声标准偏差降低了10%～35%。Dragomiretskiy等[8]提出了变分模态分解(VMD)理论。文献[9]提出了基于VMD结合小波阈值的MEMS陀螺去噪方法，对于静态信号和动态信号，该方法的均方误差降低了10.1%和16.9%。上述方法中，文献[5]表明BP神经网络优化卡尔曼滤波参数的方法，在建模不精确的情况下也能有效提高陀螺仪的精度，但BP神经网络优化参数存在局部最优的问题且不够简便[10-11]。文献[6]表明基于BP神经网络建立的补偿模型，能够对MEMS陀螺的输出进行有效补偿，但仅在低转速区间效果较传统方法更优。文献[7]单一的增强型支持向量机方法，算法简单易实现，但去噪效果有待提升，需要改进以达到更好的去噪效果。文献[9]VMD结合小波阈值的方法较为复杂，对分解层数以及阈值等各项参数的选择会影响去噪效果且方法的计算时间受模态分解速度的影响。

因此，本文提出利用BP神经网络来建立MEMS陀螺的误差模型，对MEMS陀螺的输出进行有效补偿。同时利用QPSO算法对卡尔曼滤波参数进行优化，解决BP神经网络存在的局部最优问题。通过基于BP神经网络建立的误差模型进行补偿之后，再利用优化的卡尔曼滤波进行滤波，以达到更好的去噪效果。

1 系统建模和滤波方法

1.1 BP神经网络

BP神经网络是一种多层前馈神经网络。如图1所示，BP神经网络结构由输入层、隐含层和输出层三部分组成，其中隐含层可以是1层或者多层[12]。

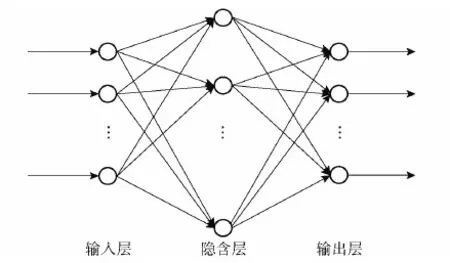
图1 BP神经网络结构图Fig.1 Diagram of BP neural network structure

BP神经网络算法的核心为误差的反向传播过程，通过采用梯度下降的方式达到调整隐含层的权重和阈值目的，使网络输出值逼近期望值，直到输出误差达到限定的水平，或达到设定的学习步数，完成网络的训练。误差函数公式如下：

(1)

式中：e为输出误差；o代表当前为第o个神经元；q为神经元总数；do0(k)为期望输出，k表示层数；yo0(k)为实际输出。BP神经网络具有自适应强、泛化能力好、非线性映射能力强的优点。

由于MEMS陀螺的随机误差往往表现为慢时变、弱非线性，传统的时间序列分析方法需要对陀螺的数据进行预处理[13]。而BP神经网络具有非线性映射能力强的优点，理论上能够逼近任意的非线性函数，无需对数据进行预处理。除此之外，BP神经网络还具有自适应性强、学习能力强的优点，已有很多国内外学者基于BP神经网络对MEMS陀螺的随机漂移误差进行建模[14]。基于上述分析，本文提出采用BP神经网络，利用BP神经网络强大的映射能力建立MEMS陀螺的误差模型，对MEMS陀螺输出进行补偿。

1.2 基于平均最优位置的QPSO

2004年，孙俊从量子力学的角度出发，提出了具有量子行为的粒子群优化QPSO[15]算法。在QPSO算法中引入了量子力学中的不确定原理，认为粒子具有量子的行为，粒子的更新是通过观测得到新的个体，使得粒子的更新与该粒子之前的运动没有任何关系，增加了粒子位置的随机性。QPSO算法中，粒子的位置迭代公式如下：

(2)

式中：xid(t+1)为第d维度的第i个粒子t+1时刻的位置；Lai为局部吸引因子，由个体最优位置和全局最优位置共同决定；β为压缩- 扩张系数，用来控制算法的收敛速度；u为0～1之间的随机数。Lai与β的表达式如下：

(3)

(4)

式中：φ为0～1之间的随机数；pid为第d维度的第i个粒子的个体最优位置；gd为第d维粒子的全局最优位置;w1、w2和c1、c2为权值；itermax为最大迭代次数；t为当前迭代次数。

对于上述QPSO，在迭代末期，群体多样性会急剧恶化，个体容易陷入局部最优，故引入了平均最优位置mbest，即所有粒子个体最优位置的平均，其表达式如下：

(5)

式中：mbest(t)为粒子t时刻的个体平均最优位置；n为粒子数；pi(t)为第i个粒子t时刻的个体最优位置。这样，基于平均最优位置的QPSO算法的粒子位置迭代公式如下：

(6)

2 卡尔曼滤波

卡尔曼滤波是一种利用线性系统状态方程，通过系统输入输出观测数据，对系统状态进行最优估计的算法，不需要存储历史数据[16]。系统的状态方程和量测方程分别为

xk=Axk-1+Buk+wk

(7)

zk=Hxk-1+vk

(8)

式中：xk为状态量；uk为输入量；wk为均值为0、方差为Q的系统噪声；zk为观测量；vk为均值为0、方差为R的量测噪声；A、B、H为已知的系统结构参数[17]。

卡尔曼滤波方程如下：

(9)

式中：Pk，k-1为一步预测均方误差矩阵；Pk，k为状态估计误差矩阵；Kk为系统增益矩阵；I为单位矩阵。

卡尔曼滤波便于计算机编程实现，并能够对实时数据进行更新和处理，目前已成为MEMS陀螺降噪常用的方法[18]。通过分析卡尔曼滤波方程，当系统噪声过大时会导致系统增益减小，使得新息对最优估计的占比减小并使得估计误差矩阵变大，最终引起滤波精度下降甚至发散。因此通过调节Q，可以在系统状态转移矩阵A不准确时，依旧使系统达到稳定[4]。同理，对R值进行合理调整，也能提高卡尔曼滤波的精度。

一般而言，卡尔曼滤波的噪声方差难以准确获得，这是因为MEMS陀螺随机漂移往往呈现弱非线性、非平稳和慢时变的特点，无法准确获得其统计特性。基于上述分析，本文提出利用QPSO算法来优化卡尔曼滤波的Q值和R值[19]。QPSO不需要粒子速度信息，控制参数少，速度更快，并且引入了平均最优位置，提高了粒子间的协作能力，相较于BP神经网络和普通的PSO算法，其全局搜索能力更高，能确定更多的状态。

3 滤波方法设计

本文提出的滤波方法原理如图2所示，首先将采集到的MEMS陀螺数据y输入训练好的误差模型，得到对应的误差信息e；然后将陀螺数据y减去得到的误差信息e，对陀螺数据进行补偿，得到补偿后的数据y′；最后将数据y′通过卡尔曼滤波滤除噪声信号，得到最终的去噪信号Y。

图2 滤波方法原理Fig.2 Principle of the filtering method

根据工程应用经验，转台数据具有精度高、线性度好、噪声小等特点，常用于客观评价MEMS陀螺的精度[20]，因此考虑将转台数据作为MEMS陀螺输出的参考值。建立MEMS陀螺仪的误差模型时，采集MEMS陀螺仪数据和转台数据作为BP神经网络的训练集，网络的输入和目标分别为MEMS陀螺仪数据和MEMS陀螺的误差信息(即陀螺仪数据减去转台数据)，对网络进行训练，建立MEMS陀螺误差模型。

利用QPSO算法对卡尔曼滤波Q值和R值优化算法流程如图3所示。

图3 QPSO算法优化卡尔曼滤波参数流程Fig.3 Flow chart of optimization of Kalman filter parameters by the QPSO algorithm

算法具体步骤如下：

步骤1相关参数初始化，包括粒子种群数n、粒子维度d、最大迭代次数itermax、粒子位置x等。

步骤2输入经过误差模型补偿的MEMS陀螺数据，作为卡尔曼滤波的输入。

步骤3在迭代中依次将粒子位置作为卡尔曼滤波的Q、R值，进行卡尔曼滤波，得到去噪后的数据，并计算适应度值。

步骤4根据初始适应度值确定初次迭代中的个体最优位置，并将此时的个体最优位置设定为全局最优位置。

步骤5进入下一次迭代，根据个体最优位置和全局最优位置更新粒子位置信息。

步骤6计算粒子的适应度值，更新个体最优位置和全局最优位置。

步骤7若满足终止条件则结束，则输出最优值作为卡尔曼滤波的最优Q、R值。否则继续重复步骤5和步骤6，直至达到最大迭代次数，输出卡尔曼滤波的最优Q、R值。

4 实验验证与分析

基于第3节方法，首先要采集误差模型建模所需的训练集数据，在室温条件下，使用专用的工装将MEMS陀螺安装在某国产三轴转台上，如图4所示。实验所用的MEMS陀螺仪为国产XC-M305型三轴MEMS陀螺仪，数据传输接口为RS-422接口，波特率为230 400 bit/s，数据更新率为2 kHz。转台由专用的测控软件控制，并且可以实时采集转台数据，采样率设定为2 kHz。实验开始，将转台z轴设置不同的转速，分别为±1.5°/s、±3°/s和±6°/s，同时采集陀螺仪和转台数据并保存。

图4 实验现场Fig.4 Experiment site

4.1 BP神经网络建模

利用BP神经网络建模，首先模型确定为一个单输入单输出的系统，输入为MEMS陀螺的实际输出，输出为预测的MEMS陀螺的误差信号。然后确定训练集样本，将同一角速度下的MEMS陀螺仪数据和转台数据作为一组数据。在采集的6组数据中，±1.5°/s组数据为12 000组，±3°/s组数据为10 000组，±6°/s组数据为6 500组。BP神经网络的训练通过MATLAB软件完成。网络的输入为MEMS陀螺仪数据，网络目标为误差信息(即MEMS陀螺数据减去转台数据所得数据)，训练集、测试集和验证集分别占比70%、15%、15%。

表1所示为不同隐含层节点数选取与对应的网络学习的均方误差值MSE。

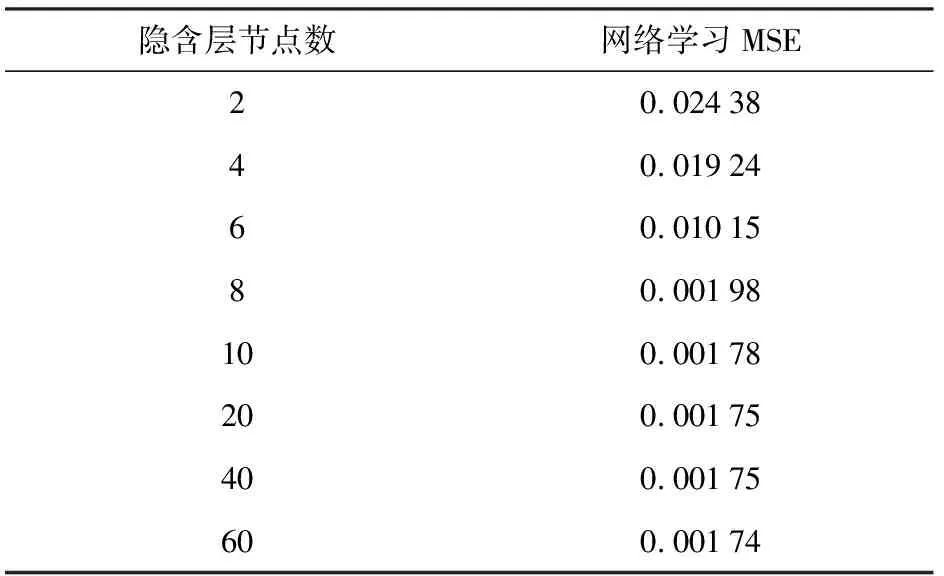
表1 隐含层节点数与网络学习均方误差Table 1 Number of hidden layer nodes and mean square error of network learning

由表1可知，当隐含层节点数为60时，网络学习的均方误差值最小。随着隐含层节点数的增加，会使得网络训练的计算量越大，所需时间越长，但数据显示当隐含层节点数选取大于10时，均方误差值减小并不显著。综合考虑，隐含层节点数选取为10，此时网络学习的综合效果最优，基于BP神经网络的MEMS陀螺仪误差模型建立完成，模型为一个单输入单输出系统，输入层与输出层神经元数目都是1，隐含层神经元为10。对该模型输入MESM陀螺的实际信号，即能返回预测的MEMS陀螺误差信号。

4.2 卡尔曼滤波参数寻优

在开始迭代之前，首先要获取经过误差模型补偿后的MEMS陀螺仪数据，依次将6组MEMS陀螺数据输入补偿模型进行补偿，之后将补偿后的数据作为卡尔曼滤波的输入，开始进行基于QPSO算法的卡尔曼滤波参数寻优。算法通过MATLAB软件实现，粒子维度d设置为2，L范围设置为[-10,10]，种群规模n设置为100，最大迭代次数itermax设置为100，权值w1、w2和c1、c2分别设置为0.5、1.0和2.2、2.2。适应度函数为经过卡尔曼滤波后所得去噪数据的MSE值，并设置MSE≤0.000 01时终止迭代。记录所得到的优化参数Q值、R值与MSE值，结果记录如表2所示。

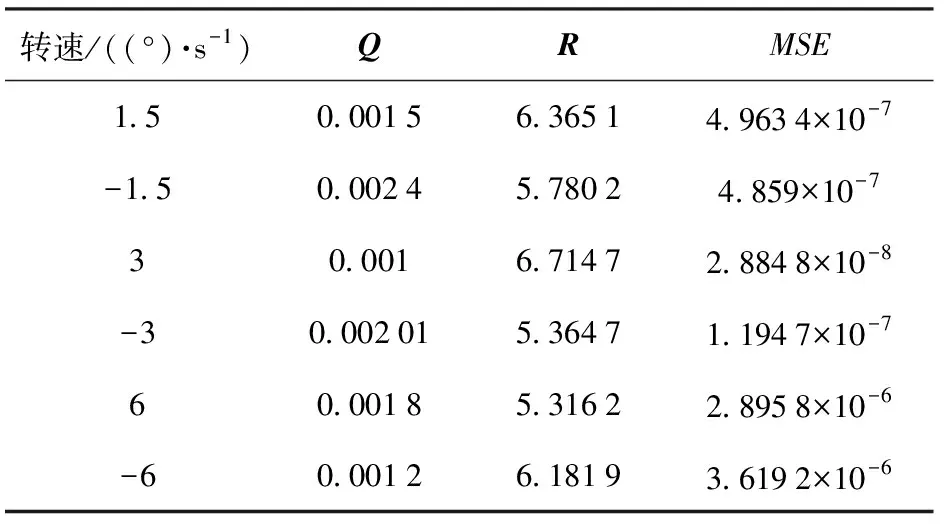
表2 QPSO优化卡尔曼滤波参数Table 2 Optimized Kalman filtering parametersby QPSO

由表2可知：对于6组不同转速下的MEMS陀螺信号，经过补偿后利用QPSO算法优化卡尔曼滤波Q值和R值，得到的Q值相对偏小，R值相对较大；不同转速下的最优Q值和R值偏差不大。说明对于不同组的数据，QPSO优化卡尔曼均能自动寻优，找到全局最优参数。

4.3 结果分析

基于4.1节、4.2节实验结果，对6组不同角速率下的MEMS陀螺数据进行去噪处理，图5所示为不同角速率下的去噪效果图。由图5可以看出，对比去噪前后的数据，本文方法对于不同角速率下的MEMS陀螺数据，均能显著改善MEMS陀螺仪的漂移误差。

为进一步比较本文方法的去噪效果，与BP神经网络优化卡尔曼滤波、QPSO优化卡尔曼滤波和VMD结合小波阈值去噪[21-23]等方法进行比较分析，结果如图6所示。

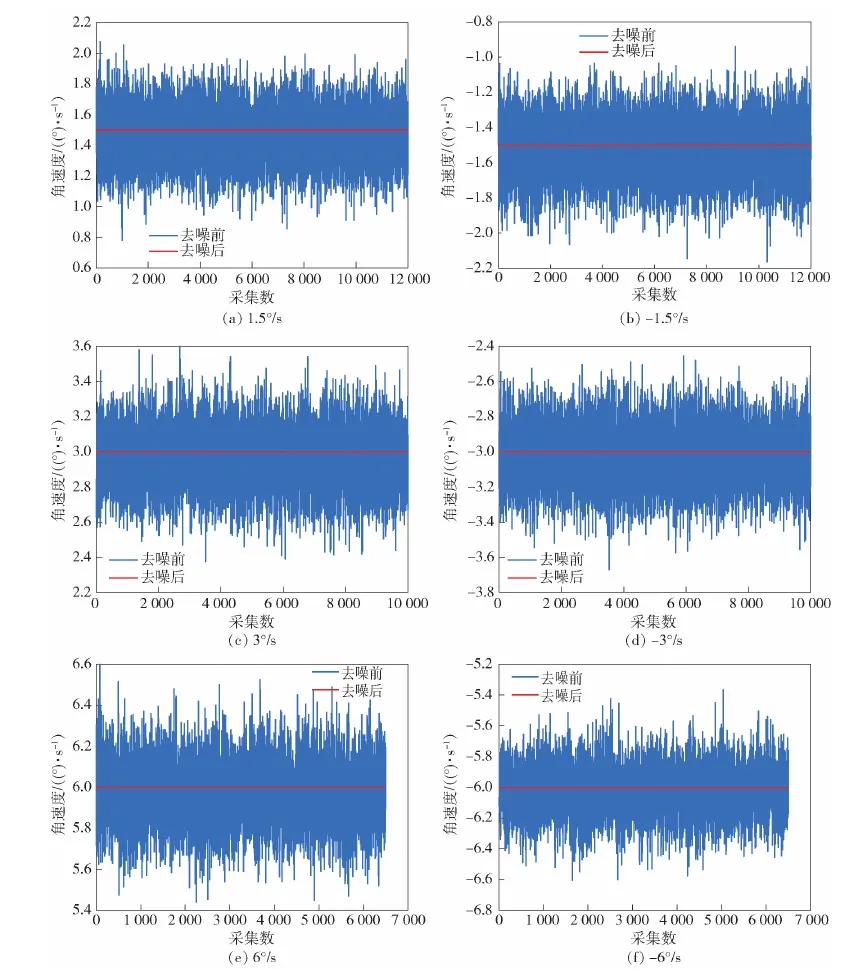
图5 不同角速率下去噪效果图Fig.5 Denoising effect under different angular rates

观察图6可以看出，4种对不同角速率下MEMS陀螺的输出均具有不错的去噪效果，与其他方法进行比较，本文方法对±1.5°/s、±3°/s和±6°/s角速度下MEMS陀螺仪输出的噪声的补偿效果更优。

为进一步评价上述方法的去噪效果，计算不同角速率条件下MEMS陀螺各组数据去噪前和去噪后的MAE和MSE值，具体的计算结果如表3所示。由表3可以看出，4种方法对MEMS陀螺数据去噪处理后，MAE和MSE值均得到了不同程度的降低，本文方法对陀螺仪数据去噪后的MAE和MSE值均为最小，且在不同测试条件下MAE值比另外3种方法小了一个数量级以上，MSE值比另外3种方法小了3个数量级以上，表明本文提出的方法去噪效果优于其他3种方法。

图7为使用本方法去噪前后的MEMS陀螺和某国产三轴挠性陀螺，在相同角速率下的z轴输出对比图。从图7中可以看出，在当前实验环境下，经过本文方法去噪处理后的MEMS陀螺仪输出信号的误差比挠性陀螺输出信号误差更小，表明本文方法能确实抑制MEMS陀螺仪的噪声，提高其精度和性能。

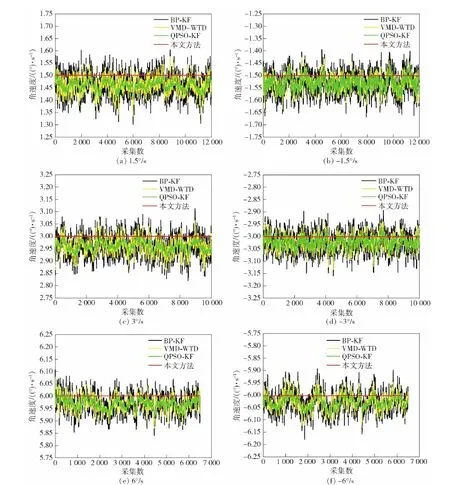
图6 不同角速率下不同方法去噪效果图Fig.6 Different methods of denoising at different angular rates 表3 不同方法MAE与MSE结果对比Table 3 Comparison of MAE and MSE results by different methods

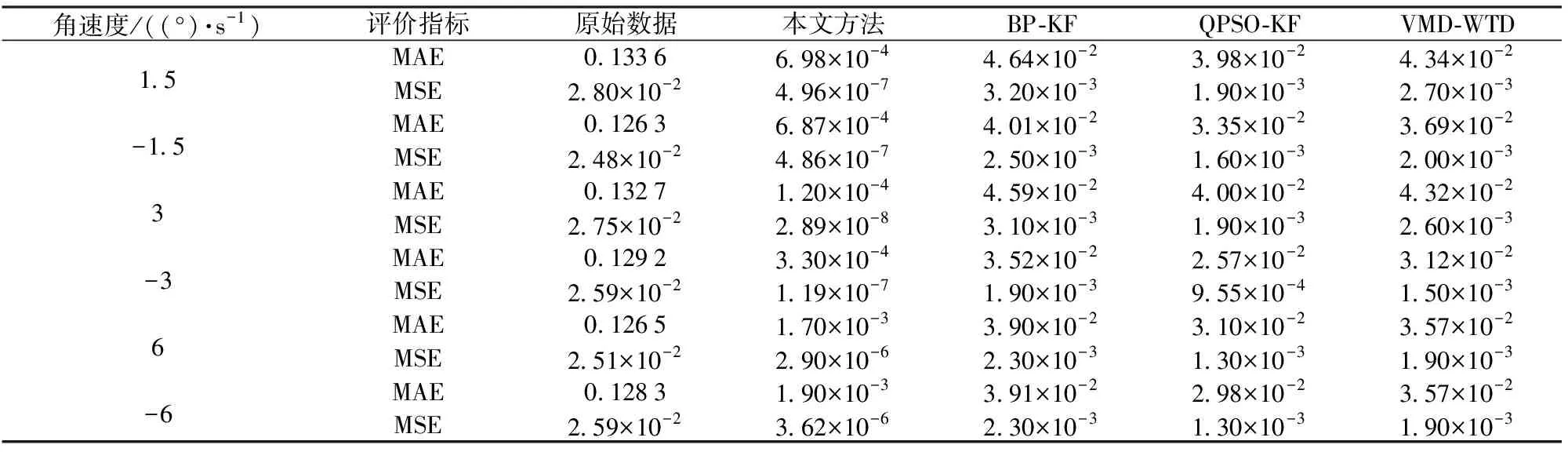
角速度/((°)·s-1)评价指标原始数据本文方法BP-KFQPSO-KFVMD-WTD1.5MAE0.13366.98×10-44.64×10-23.98×10-24.34×10-2MSE2.80×10-24.96×10-73.20×10-31.90×10-32.70×10-3-1.5MAE0.12636.87×10-44.01×10-23.35×10-23.69×10-2MSE2.48×10-24.86×10-72.50×10-31.60×10-32.00×10-33MAE0.13271.20×10-44.59×10-24.00×10-24.32×10-2MSE2.75×10-22.89×10-83.10×10-31.90×10-32.60×10-3-3MAE0.12923.30×10-43.52×10-22.57×10-23.12×10-2MSE2.59×10-21.19×10-71.90×10-39.55×10-41.50×10-36MAE0.12651.70×10-33.90×10-23.10×10-23.57×10-2MSE2.51×10-22.90×10-62.30×10-31.30×10-31.90×10-3-6MAE0.12831.90×10-33.91×10-22.98×10-23.57×10-2MSE2.59×10-23.62×10-62.30×10-31.30×10-31.90×10-3

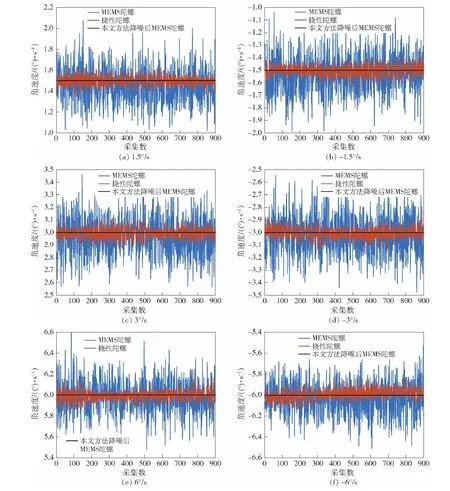
图7 不同角速率下挠性陀螺与MEMS陀螺对比图Fig.7 Comparison of flexible gyro and MEMS gyro at different angular rates

5 结束语

本文针对MEMS陀螺仪随机误差相对较大、影响其精度这一问题，提出了一种基于BP神经网络结合QPSO算法优化卡尔曼滤波的补偿方法。首先利用BP神经网络建立MEMS陀螺的误差模型，并对陀螺数据进行补偿，补偿后的数据再通过QPSO算法优化的卡尔曼滤波进行去噪。实验结果表明：本文方法具有很好的去噪效果，并与BP神经网络优化KF、QPSO优化KF和VMD结合WTD去噪方法进行比较，本文提出方法的MAE和MSE值相较上述方法更小，并且在当前实验环境下与挠性陀螺仪相比噪声误差也更小。因此，本文提出的方法是有效的，对实际工程应用具有一定借鉴意义。