基于微分平坦的分层轨迹规划算法
2023-03-21周孝添任宏斌苏波齐志权汪洋
周孝添, 任宏斌, 苏波, 齐志权, 汪洋
(1.北京理工大学 机械与车辆学院, 北京 100081; 2.中国北方车辆研究所, 北京 100072)
收稿日期:2021-11-09
基金项目:国家自然科学基金项目(52002025)
0 引言
在人工智能的热潮之下,智能汽车行业的发展也受到社会的广泛关注,因为它将在降低交通事故发生率、减少交通拥堵、改善大气环境、降低能源消耗等方面做出重要贡献[1]。无人驾驶汽车是智能汽车发展的高级阶段,避障轨迹规划作为无人驾驶技术最核心的技术之一,对无人驾驶车辆的研究具有重大意义。在结构化道路下,其基本任务是考虑车辆与前方障碍物的几何关系,规划出一条避免发生碰撞的换道轨迹,同时应该具有较高的乘坐舒适性,从而提高出行效率[1-2]。
针对结构化道路下的变道避障轨迹规划,国内外学者进行了各种研究[3-9]。Zhang等[4]和聂枝根等[5]利用三角函数去模拟车辆变道轨迹,此算法虽然简单高效,但忽略了运动学约束,且存在变道终点已知的局限。Kanaris等[6]提出一种基于正反梯形横向加速度的方法,通过对横向加速度优化求解、积分得到变道轨迹,此方法虽然有效结合了车辆横向运动学,但不够灵活,无法高效地调节整个变道过程。牛国臣等[7]设计了一种双5次多项式换道避障轨迹规划算法,虽然此算法通过优化换道时间来改善乘坐舒性,但忽略了横纵向耦合对行驶安全性乘坐舒适性的影响。Li等[8]设计了一种基于多阶贝塞尔曲线的变道避障路径规划方法,此方法虽然能有效地调节变道效率和乘坐舒适性之间的平衡关系,但只适用于恒速变道。Shim等[9]设计了横纵向上关于时间的6阶多项式模型,通过求解非凸目标函数得到了期望轨迹,虽然此方法考虑了乘坐舒适性和运动学约束,但因为是一个非凸优化过程,所以求解效率较低,实用性差。
近年来,微分平坦定理在无人机和无人车运动规划中得到的广泛关注,其主要优点是能将非线性系统的微分约束映射为平滑集合约束,有效减少了优化空间的维数[10-12]。Cong等[10]利用车辆系统的平坦输出建立运动学和稳定性约束来弥补基本质点模型规划算法的不足。Wang等[11]利用车辆动力学模型的微分平坦特性线性化车辆非线性动力学模型,大大提高了预测控制精度。Guo等[12]基于微分平坦定理提出了一种具有轮胎稳定性控制的最大功率控制器。
综上所述,目前运动规划问题普遍都是把三维的轨迹规划(横向- 纵向- 时间)解耦为两个二维规划问题,但McNaughton等[13]认为解耦会损失车辆运动的最优性。由于在横纵向轨迹设计时并没有考虑其耦合性,为提升规划算法的最优性且能满足更多的运动学约束,本文提出一种分层段轨迹规划算法,在底层构建以贝塞尔曲线(Bézier curve)节点为自变量且满足避障、速度、加速度约束等凸约束的二次规划问题,保证算法的概率完备性和行车安全性。利用车辆运动学的微分平坦特性,构建以乘坐舒适性、运动学约束、能耗、行车效率等指标的目标函数,利用粒子群优化(PSO)算法优化终止车速和行驶时间,得到一条满足车辆多目标约束的行驶轨迹。
1 基于贝塞尔曲线的局部路径规划
1.1 贝塞尔曲线
贝塞尔曲线是应用于二维图形应用程序的数学曲线[14]。曲线定义起始点、终止点(也称锚点)、控制点。通过调整控制点,贝塞尔曲线的形状会发生变化。故基于贝塞尔曲线进行避障规划是通过寻找贝塞尔曲线控制点的最优位置来实现避障。已知贝塞尔曲线方程为
(1)
(2)
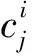
从上述推导可知,贝塞尔曲线本质是关于变量t的多项式,由于形状由每个节点的坐标决定,具有如下性质:
1)它总是从第1个控制点开始,到最后一个控制点结束,不经过中间其他节点,但是曲线始终在所有节点连接构成的凸多边形内。
2)曲线每个节点的导数由曲线节点的线性组合求得,即曲线的导数同样也可以被约束在凸多边形内。
3)曲线自变量t的区间为[0,1]。
1.2 避障轨迹规划
根据贝塞尔曲线形状可知,当给定控制点范围约束时,可以保证整条曲线都位于此安全范围内,利用此性质大大减少了约束的数量,提升了求解效率.如图1所示,图中点划线为两车道的中心线,黑色虚线为车道分割线,由于静态障碍物和动态障碍物的存在,贝塞尔曲线节点的可行域是一个非凸域。为了使算法的求解效率更高,在非凸域上构造两个凸的安全走廊,以两段7阶贝塞尔曲线构造变道曲线,变道起点和变道终点都位于车道中心线上,则把原始的非凸优化问题转化为在两个安全走廊的凸优化问题。
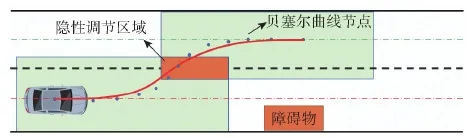
图1 避障轨迹规划Fig.1 Obstacle avoidance trajectory planning
由于贝塞尔曲线时间的取值在[0,1]内,故需要对曲线进行归一化,则实际变道曲线函数[15]为
(3)
式中:s1、s2为每一段贝塞尔曲线对应的实际时间;μ∈{x,y}表示横向和纵向两个方位。
由于贝塞尔曲线的安全走廊存在一定范围内的重叠,使得优化问题具有更高的自由度,对每一段贝塞尔曲线时间分配进行隐性调节。把三维空间中的轨迹规划问题分解为两个二维空间中的贝塞尔曲线优化问题,建立以曲线3次导数的平方和为目标函数:
(4)
式中:T为贝塞尔曲线对应的时间;τ为仿真时间,τ∈[0,1],节点编号i∈{0,1,2,3,4,5,6,7};j∈{1,2}表示两段贝塞尔曲线。
设节点i的第f阶导数为
(5)
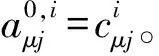
(6)
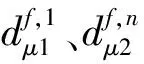
由于轨迹是由两段曲线拼接而成,需要设置连续性约束:
(7)
由式(7)可知通过保证第1段曲线末尾节点与第2段曲线起始节点的初始位置、速度加速度相等来保证连续性约束。
为保证行车安全行,避免与障碍物发生碰撞,需要添加边界约束:
(8)
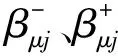
实际车辆行驶过程中受到运动学约束,需要对横纵方向上的速度、加速度进行约束:
(9)
(10)
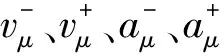
由于目标函数是一个二次型,且约束条件都是凸的,上述贝塞尔曲线优化问题是一个凸二次规划问题,求解效率极高。但是此问题的求解需要给定确切的行驶时间和末端车速,是一个局部条件下的最优问题。为使求得的轨迹全局最优,下面利用PSO算法对对参数进行优化,同时在适应度函数中加入乘坐舒适性和可跟踪性等度量函数。
2 车辆运动学模型的平坦输出
微分平坦最早是由法国Martin提出的优化微分代数的概念[15],之后得到迅速发展并慢慢引入控制领域。近年来广泛运用于复杂约束的路径规划问题中,对于一个非线性系统:
(11)
如果能找到如下形式的输出量:
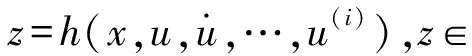
(12)
使得系统的状态量以及输入量都能用输出量z和z的有限阶导数表示:
(13)
则称系统是微分平坦系统。其中x为系统状态量、y为系统输出量、u为系统控制量,n、m分别为维度数量,F(x,u)表示非线性状态方程,g(x)表示非线性输出方程,z为平坦系统的平坦输出,h为平坦函数,由于平坦输出与状态变量和控制输入之间是一一对应的关系,微分平坦的运动特征可以由平坦输出唯一决定。这样就把一个高维状态空间映射到了平坦空间,降低了规划空间维度,如图2所示。图2中,x(T)、u(T)为末尾状态,x(0)、u(0)为初始状态,F(0)=h(x(0),u(0))与F(T)=h(x(T),u(T))分别为平坦空间的初始状态和末尾状态。
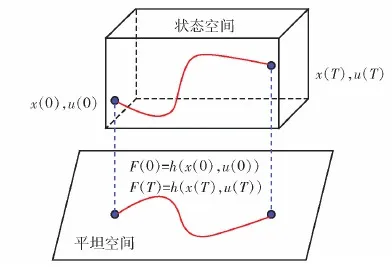
图2 状态空间与平坦空间的映射关系Fig.2 Mapping between state space and flat space
为进一步优化利用汽车的非完整性运动学约束得到的贝塞尔曲线,建立图3所示车辆运动学模型,其中前轮为转向轮、后轮为驱动轮,以后轴线中心为参考点建立坐标系,(x,y)为车体位置坐标,δ为前轮转角,φ为车辆横摆角,q=[x,y,δ,φ]为车体的位姿向量,R为转弯半径,l为前后轴轮距。
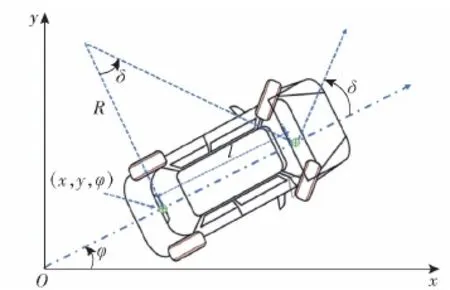
图3 车辆运动学模型Fig.3 Vehicle kinematics model
则车辆的非完整性约束为
(14)
式中:(xf,yf)为前轮中心坐标。上述等式表示前后轴无侧向滑动,满足如下几何关系:
(15)
根据阿克曼转角的几何关系可以得到转弯半径R:
(16)
式中:ρ为曲率半径。
以车辆状态向量作为状态量,以车速v和前轮转角的角速度ω为模型输入量,建立如下运动学模型:
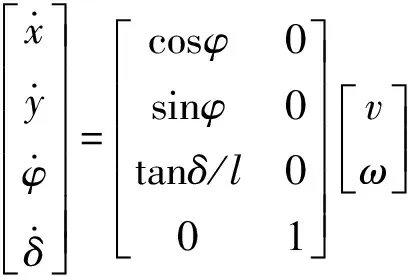
(17)
已知横纵向的贝塞尔曲线表达式为
(18)
(19)
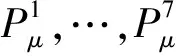
(20)
式中:α、β矩阵由横纵向贝塞尔曲线节点cx、cy确定。
由运动学模型可得
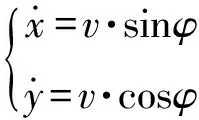
(21)
进一步推导可得
(22)
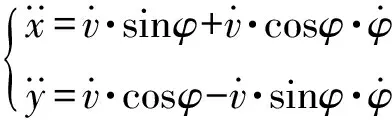
(23)
由式(21)和式(23)可得横摆角速度:
(24)
从而可以得到前轮转角表达式:
(25)
3 基于粒子群的二次优化算法
贝塞尔曲线优化问题是基于质点模型的凸优化,但对于车辆这样一个非完整系统,应该将车辆的运动学和输入输出状态约束考虑在内,保证规划轨迹具有很高的可执行性,否则会极大程度地增加轨迹跟踪的难度。而且基于贝塞尔曲线的轨迹规划问题只满足避障和部分运动学等硬约束和部分平顺性约束,因为目标函数属于车辆平顺性的子集。为规划出一条安全行、高效性、舒适性、可执行性等综合性能最优的贝塞尔曲线,本文利用微分平坦输出设计满足上述条件的目标函数,由于目标函数对初始参数没有明确的梯度表达式,利用PSO算法[16]完成对底层凸优化问题的初始参数行驶时间s1、s2和最终车速vt的在线优化,最终得到一条综合性能最优的行驶轨迹。具体流程算法流程如图4所示。图4中,k为当前迭代次数,F为自适应函数,Ft1,Ft2,…,Ft6为粒子适应度,Xij为种群位置,vij为种群速度,s1k,s2k,…,stk为每段贝塞尔曲线对应的时间,gb为粒子在所有迭代周期内的全局极值,Pib为粒子的个体极值。
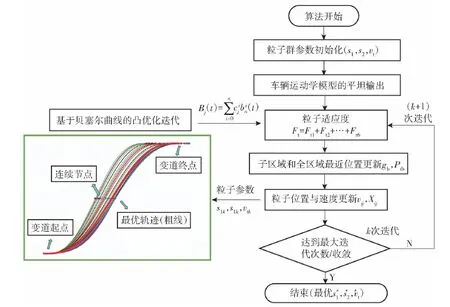
图4 算法流程Fig.4 Flow chart of the algorithm
首先设置粒子群内的粒子数np,由此可得粒子群矩阵如下:
X=(X1,X2,…,Xnp)
(26)
种群中每一个粒子包含3个参数:
Xi=(s1,s2,vt),i=1,2,…,np
(27)
考虑粒子群内所有粒子在所有迭代周期内的全局极值、每个粒子维度下的速度和个体极值:
9月14日育苗,10月30日移栽,6行区,行长6.4米,行距0.5米,每小区面积19.2平方米,每亩密度4 000株。全生育期不进行中耕除草,仅是每次施氮肥时均用水浇施,提高肥效。在水稻收获后不进行稻田翻犁,直接开行移栽油菜。重复间开沟,沟宽40厘米,沟深30厘米。2个品种随机区组排列,3次重复。
(28)
在迭代过程中粒子会根据自身粒子的惯性,以及与自身极值Pi和全局极值gb之间的距离来更新自身的速度vi和位置Pi:
(29)
(30)
式中:j=1,2,3;ω为惯性权重因子;c1、c2为自身权重因子和种群权重因子;r1、r2分别为大小在[0,1]之间的2个随机正整数。
从轨迹安全行、高效性、舒适性、可执行性等各项性能出发设计自适应函数Ft。首先考虑行车安全行,可由贝塞尔曲线与障碍物间的曼哈顿距离评价:
Ft1=ω1dist(obs,Bezier)
(31)
式中:ω1为指标权重系数;obs表示周边障碍物的全局坐标。
横向乘坐舒适性指标是前轮转角及其变化率,纵向舒适性评价指标为纵向加加速度,则总的舒适性评价指标为
(32)
式中:ω2、ω3为指标权重系数;xj、yj分别为横纵向坐标;g为重力加速度。
由于轨迹规划与控制模块分离在不同的层中,导致二者的目标侧重不是完全切合,一般假设当轨迹满足一定约束条件时底层控制能够以有界的误差跟踪轨迹。然而由于车辆模型的误差 ,可能会使得规划层规划出不符合运动学约束的轨迹,一般用最大曲率ρmin=0.1 m-1进行限制[17],为加快PSO算法收敛速度,运用Sigmoid函数[18],设计可执性评价指标:
(33)
式中:ω4为指标权重系数。
(34)
式中:μy为轮胎的横向附着系数,对于干燥路面,一般μy取1[20];φmax为最大偏航角;βmax为最大质心侧偏角。
同理,利用Sigmoid函数设计质心侧偏角和横摆角速度评价指标:
(35)
(36)
式中:ω5、ω6为指标权重系数。
在实际的结构化道路上行驶时,在保证智能汽车乘员舒适性前提下,变道避障时间越短越好,这样能够在宏观层面上提高交通效率,设计避障效率指标为
Ft6=ω7·s1+ω8·s2
(37)
式中:ω7、ω8为指标权重系数。故粒子自适应函数为
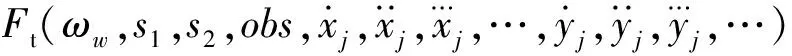
(38)
式中:w为贝塞尔曲线的粒子数,w∈{1,2,…,8}。式(31)~式(38)中,指标权重系数ω1,ω2,…,ω8根据不同的驾驶风格进行选取。
4 数值仿真实验
换道避障是自动驾驶汽车实现结构化道路上无人驾驶的基础技术,双移线避障又可以看作单移线的叠加和改进。因此在考虑周围静态和动态车辆的环境下,如何规划出一条综合性能最优的行驶轨迹,就成为结构化道路下局部路径规划技术的关键。
如图5所示,车辆A以va=47 km/h的车速向前行驶,与前方障碍车辆C相距lac=30 m时发现前方车辆车速急剧降低,此时车辆做出换到避障决策,左侧车道车辆B车速为vb=40 km/h,相距lab=20 m,左侧车道车辆D车速为vd=40 km/h,相距lad=40 m,车辆C的车速为vc。本文采用谨慎型驾驶风格进行轨迹规划[21],由第2节可知,安全走廊重叠区域的作用是对行驶时间和乘坐舒适性的隐性调节,因此安全走廊的宽度取值一般比车道有效宽度略大一些,一般取值为1.25D(D为车道有效宽度),故安全走廊的宽度边界为
(39)
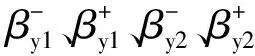
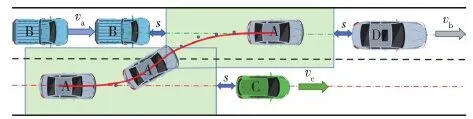
图5 变道避障示意图Fig.5 Schematic diagram of obstacle avoidance by lane changing
由于算法有性调节优化参数功能,安全边界按照车辆以最小能耗,即原始车速行驶进行计算。根据文献[22]取安全距离s=5 m,则在第一段安全走廊行驶的最大时间为
(40)
第1段和第2段安全走廊的消耗最大时间为
(41)
由式(41)和式(42)可得纵向安全走廊边界为
(42)
式中:v为本车车速。取粒子数np=5,则粒子群初始化参数为
(43)
在MATLAB 2020a软件中进行轨迹规划仿真,并搭建基于模型预测控制的Simulink模型和车辆动力学仿真软件Carsim进行轨迹跟踪仿真,对规划得到的轨迹和轨迹跟踪得到的仿真轨迹性能进行对比验证,同时增加与基于采用的5次多项式轨迹[23]的对比分析。换道仿真的相关参数如表1所示。
4.1 迭代优化仿真
图6为5次多项式采样算法的仿真过程,图6(a)为在三维空间的采样图,把其投影到横纵向坐标系中得到图6(b),最优5次多项式的仿真时间为t=3.55 s,终止车速为v=59.04 km/h,终止坐标为(52 m,5.4 m)。基于微分平坦分层轨迹规划仿真结果如图7所示,图7(a)为PSO算法寻找综合性能最优的避障换道轨迹过程中产生的轨迹曲线簇。由图7(b)可知PSO算法收敛速度很快,基本上可以保证在10次迭代以内收敛,因为此算法在基于贝塞尔曲线的凸优化中加入了隐性调节约束,即安全走廊的重叠区域,隐性调节了两段贝塞尔连接点的位置使求解出来的轨迹更加平滑,故加速了PSO算法的收敛速度。当粒子群适应度值收敛时,得到综合性能最优变道轨迹如图7(c)所示,两段贝塞尔曲线连接点的坐标为(22.26 m,3.229 m),终点坐标为(52.55 m,5.4 m),每段曲线对应的行驶时间分别为t1=1.65 s,t2=1.94 s。

表1 仿真实验参数Table 1 Simulation experiment parameters
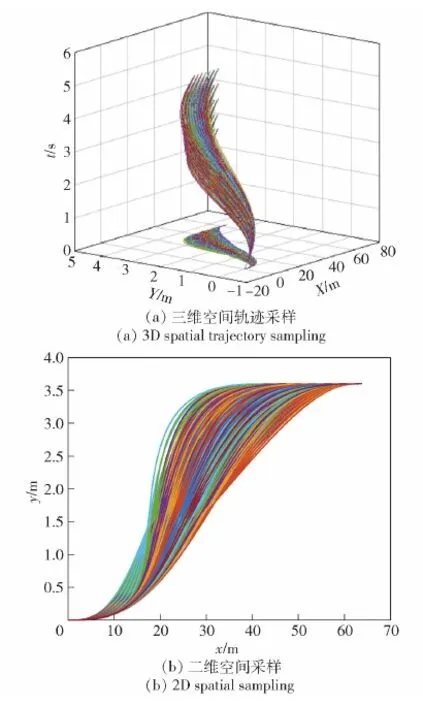
图6 5次多项式采样过程Fig.6 Quintic polynomial sampling process
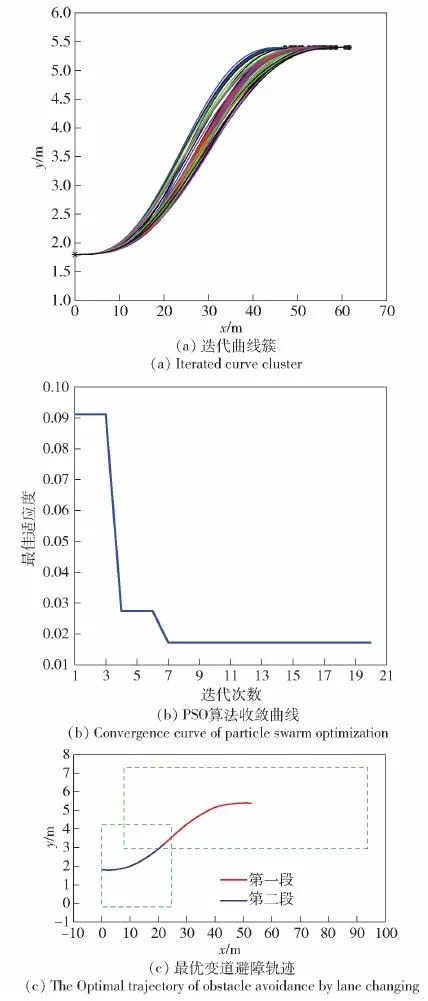
图7 基于微分平坦分层轨迹规划仿真过程Fig.7 Simulation process of hierarchical trajectory planning based on differential flatness
4.2 硬件在环验证
为验证本文规划算法的实际性能,搭建图8所示硬件在环(HIL)实验平台。根据车辆参数在Carsim中搭建车辆动力学模型,通过dSPACE提供实时接口(RTI),利用DS1006处理板在dSPACE/Autobox中下载Carsim建立的模型。在Simulink软件中搭建基于车辆3自由度跟踪误差模型的模型预测控制器[24],整个模块由模型预测控制器、车辆动力学模型、输出及观测器三大模块组成[25],并把分层轨迹规划算法与轨迹跟踪算法进行集成,然后通过MATLAB/Simulink软件提供的实时工作空间(RTW),将算法以C代码的形式下载到车辆控制器中。利用CAN总线实现dSPACE/Autobox与车辆控制器之间信息通信,在获得车辆状态信息后,车辆控制器将控制命令发送到dSPACE/Autobox。上位机的控制台接口可以通过TCP/IP或CAN-bus实现对车辆状态的监控和参数调整。仿真变道过程如图9所示,其中红线为传感器测量到与周边障碍车的距离。从图9中可以看出,规划的轨迹能在优化得到的时间内完成避障变道,且不存在任何碰撞风险。
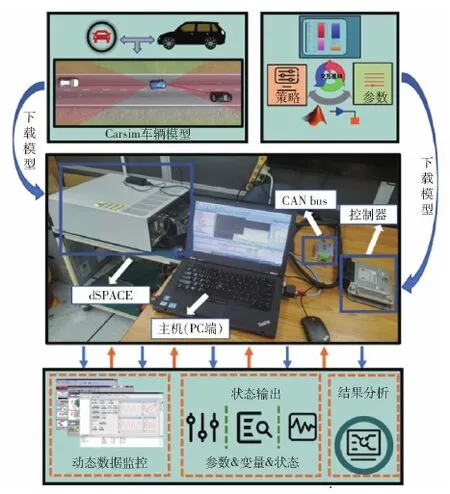
图8 硬件在环(HIL)实验平台Fig.8 Hardware-in-the-loop (HIL) experimental platform
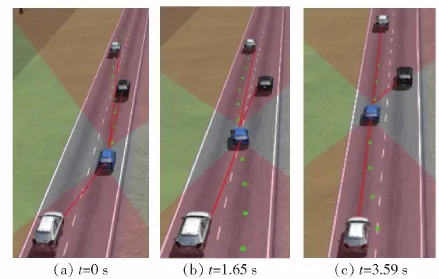
图9 变道仿真过程Fig.9 Lane changing simulation process
换道轨迹跟踪仿真结果如图10所示。从图10(a)中轨迹跟踪结果可知,规划层规划得到的轨迹可跟踪性高,仿真得到的轨迹跟踪误差较小。从图10(b)换道速度跟踪结果图可知:速度跟踪整体误差较小,可跟踪性较好,其横向跟踪误差的最大值为0.021 m;车速的最大跟踪误差为0.39 km/h,在初始时刻车速会略微下降是因为刚开始转向时会使车速降低,但车辆会迅速跟上规划得到的速度曲线,速度曲线整体平滑、没有突变,能实现无碰撞变道避障。
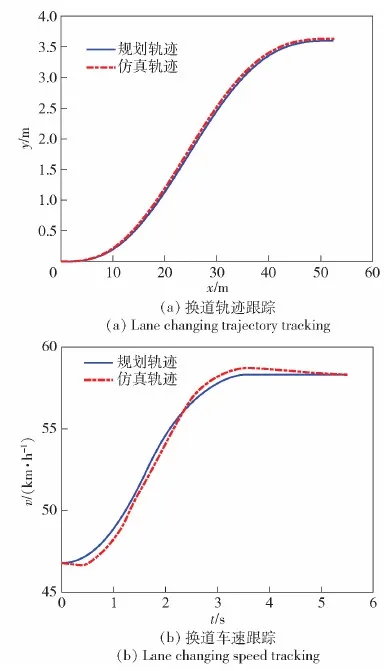
图10 换道轨迹跟踪仿真结果Fig.10 Simulation results of lane changingtrajectory tracking
基于迭代得到的最优换道轨迹的最优换道时间和速度进行5次多项式规划,二者的车辆换道性能参数如图11所示。图11(a)所示的前轮转角曲线整体平滑,符合驾驶员变道过程中前轮转角的变化趋势,Bezier规划得到的前轮转角曲线更为平滑,且最大值为1.32°,而五次多项式规划得到的前轮转角最大值为1.42°;图11(b)为换道避障过程中的侧向加速度曲线,从中可知二者得到的侧向加速度都小于阈值0.4g,车辆具有良好的稳定性;图11(c)为换道避障过程中的质心侧偏角曲线,其中Bezier规划得到的最大质心侧偏角为4.53°,5次多项式规划得到的最大质心侧偏角为5.23°,二者均小于阈值8.88°;图11(d)为换道避障过程中的横摆角速度曲线,从中可知二者规划得到横摆角速度均远小于阈值,具有良好的可跟踪性。综上所述可知,Bezier规划得到的车辆换道避障性能更优,具有更平滑、更佳的可控性。
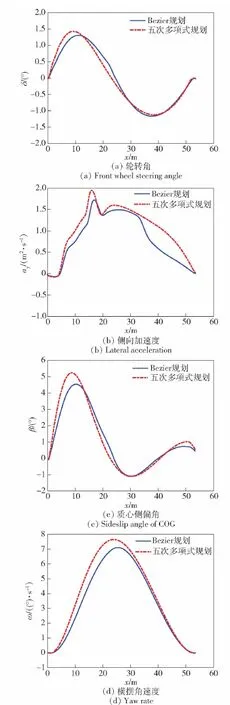
图11 车辆换道性能参数Fig.11 Lane changing performance parameters of the vehicle
5 实车换道实验
将算法应用于无人驾驶平台进行实车实验如图12所示。实际换道交通场景如图13所示,设定与前方障碍物车辆距离为30 m进行换道轨迹规划并对得到的轨迹进行跟踪。考虑到实际平台的特性和实验安全性,取初始车速20 km/h。

图12 无人驾驶平台Fig.12 Self-driving platform

图13 换道交通场景Fig.13 Lane changing traffic scene
图14为换道轨迹跟踪结果。从图14(a)中可以看出:跟踪轨迹在整体趋势下遵循参考轨迹,跟踪误差最大值为0.12 m,规划层规划得到的路径的可跟踪性能高;图14(b)表明,实际无人驾驶平台可以跟踪上规划层规划得到的速度轨迹,速度曲线符合车辆运动特性,跟踪误差最大值为0.4 km/h;由图14(c)可知,规划的轨迹可执行性高,前轮转角曲线平滑适合无人驾驶车辆进行控制,最大误差0.21°;此外运动过程中与障碍物车辆保持4 m以上的安全距离。综上所述可知,基于微分平坦的分层轨迹规划算法得到的路径曲线和速度曲线符合车辆运动学特性且具有良好的可跟踪性。
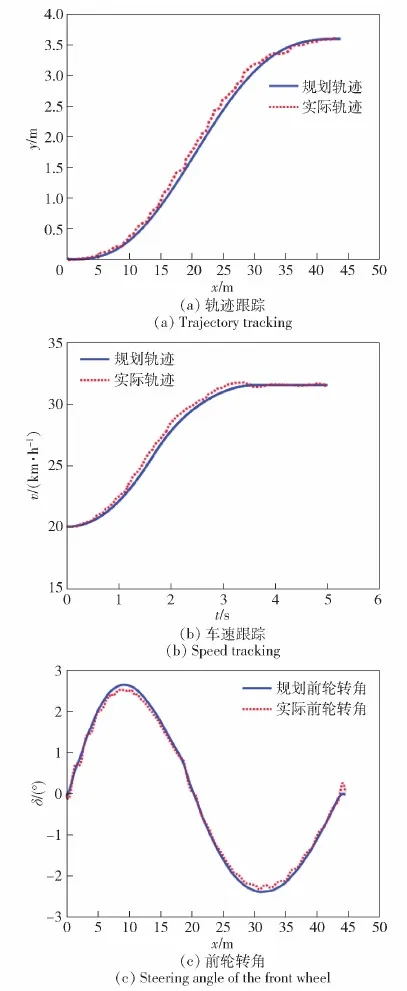
图14 换道轨迹跟踪结果Fig.14 Tracking result for lane changing trajectory
6 结论
本文提出一种基于凸二次规划和粒子群进化优化的分层段轨迹规划算法。利用贝塞尔曲线的凸包性,设计安全走廊约束,把不规则的非凸可行域划分为两个凸的可行域,以轨迹平滑性为目标函数构建一个凸二次规划器。以底层规划器得到的横纵向贝塞尔曲线构建车辆运动学模型的平坦输出,得到系统的输入量和状态量的表达式,从而可以建立行车安全行、高效性、舒适性、可执行性的自适应函数,利用PSO算法去优化基于贝塞尔曲线的凸优化的先决条件,最终搜索到一条综合性能最优的变道避障轨迹。通过与基于采用的五次多项式算法进行对比可知,所提出的算法得到的轨迹综合性能更优。
该算法通过微分平坦定理把车辆状态量集成到轨迹规划过程中,并通过底层凸优化上层进化优化的框架来保证算法的概率完备性和最优性。未来将进一步研究结合数据驱动和车辆动力学的微分平坦的轨迹规划算法,用于提升极端工况下无人驾驶车辆的规划控制性能。
