利用能量观念 速解传送带问题

■山东省德州市第一中学 李宁宁 刘立毅(正高级教师)

■山东省德州市教育科学研究院 岳志国

传送带问题是以真实的物理现象为情境的物理模型,下面从传送带的设置方向、维度等方面归纳了三种情况,探究利用能量观念求解此类问题的方法,供大家参考。

一、水平一维传送带问题

求解传送带问题,务必弄清物体的运动情况。当物体无初速度地放到水平传送带一端时,物体可能一直做匀加速运动至另一端;也可能先做匀加速运动后做匀速运动至另一端。当物体滑上传送带一端的初速度与传送带速度反向时,物体可能一直做匀减速运动至另一端;也可能先做匀减速运动再反向做匀加速运动至同一端。

例1如图1所示,水平传送带A、B两端间的长度x=8 m,轻轻地把货物放到传送带上的A端,每次传送货物(可视为质点)的质量m=2 kg,货物与传送带之间的动摩擦因数μ=0.1,取重力加速度g=10 m/s2。

图1

(1)若传送带以速度v1=2 m/s沿顺时针方向转动,求货物从传送带A端运动到B端所用的时间。

(2)若传送带以速度v2=5 m/s沿顺时针方向转动,求货物由传送带A端运动到B端的过程中,因摩擦而产生的热量。

(3)若传送带以速度v3=2 m/s沿顺时针方向转动,货物以初速度v0=4 m/s从A端滑上传送带,求货物由传送带A端运动到B端的过程中,货物对传送带做的功。

(4)某次工人错将货物以速度v0＇=3 m/s从A端滑上传送带,及时发现错误并让传送带以速度v4=2 m/s沿逆时针方向转动,求货物离开传送带时的速度和运送这件货物电动机多消耗的电能。

解析：(1)设货物做匀加速运动时的加速度为a,根据牛顿第二定律得μmg=ma,解得a=1 m/s2。货物做匀加速运动所用的时间t1==2 s,发生的位移x1==2 m。之后货物以速度v1=2 m/s做匀速运动,发生的位移x2=x-x1=6 m,所用的时间t2==3 s。因此货物从传送带A端运动到B端所用的时间t=t1+t2=5 s。

(2)货物由静止加速到速度v2=5 m/s需要发生的位移,根据位移公式得,解得货物在传送带上运动的时间t3=4 s,这段时间内传送带的位移x带1=v2t3=20 m,货物与传送带的相对位移Δx=x带1-x=12 m,因摩擦而产生的热量Q=μmg·Δx=24 J。

(3)货物做匀减速运动时的加速度大小a＇=1 m/s2,货物做匀减速运动到与传送带达相同速度发生的位移x4==6 m＜x,因此货物与传送带达到共速前没有离开传送带。货物做匀减速运动所用的时间t4==2 s,这段时间内传送带的位移x带2=v3t4=4 m,因此货物对传送带做的功W=μmg·x带2=8 J。

(4)货物做匀减速运动发生的位移x5==4.5 m＜x,因此货物离开传送带时的速度v离=2 m/s,方向由B端指向A端。货物做匀减速运动的时间t5==3 s,做匀加速运动所用的时间t6==2 s,传送带的位移x带3=v4(t5+t6)=10 m,因此运送这件货物电动机多消耗的电能E电=μmg·x带3=20 J。

点评:当v0(物速)＜vn(带速)时,根据可以求得货物运动到传送带B端恰好达到传送带的速度vn的临界带长临界时间货物的实际运动情况存在两种可能:①若带长L＜L0,则货物一直做匀加速运动,在B端离开时的速度v离=,运动时间,传送带相对货物向右的位移大小,因摩擦而产生的热量Q=μmg·Δx;②若带长L＞L0,则货物先做匀加速运动后做匀速运动,在B端离开时的速度v离=vn,运动时间t=t0+当v0(物速)＞vn(带速)时,同理得临界带长临界时间货物的实际运动情况也存在两种可能:①若带长L＜L0＇,则货物一直做匀减速运动,在B端离开时的速度v离=运动时间t0＇;②若带长L＞L0＇,则货物先做匀减速运动后做匀速运动,在B端离开时的速度v离=vn,运动时间当货物速度v0＇与传送带速度vn反向时,货物可以从A端向左或从B端向右离开传送带,推理论证如下:设货物运动至B端时,速度恰好减为0,则对货物有-μmgL0″=0-,解得临界带长①当带长L＜L0″时,货物一直向右做匀减速运动,根据-μmgL=可以求得货物从B端离开时的速度②当带长L＞L0″时,货物返回A端后离开,若v0＇≤vn,则货物从A端离开时的速度vA=v0＇,若v0＇＞vn,则货物从A端离开时的速度vA=vn。货物从A、B哪端离开传送带为隐含条件,需要根据v0＇、vn、μ及带长等物理量之间的关系通过逻辑推理才能判断出。

二、倾斜传送带问题

求解倾斜传送带问题,需要特别注意物体所受摩擦力发生突变而导致的运动状态改变。当物体无初速度地放在倾斜传送带上端时,物体可能以恒定加速度运动至底端,也可能做加速度不同的两段匀加速运动至底端。

例2如图2甲所示,倾斜传送带以恒定的速率沿逆时针方向运行。t=0时刻,将质量m=1 kg的物块(可视为质点)无初速度地放在传送带的最上端A点,经过Δt=1.0 s,物块从最下端的B点离开传送带。取沿传送带向下为速度的正方向,则物块的速度随时间变化的图像如图2乙所示,取重力加速度g=10 m/s2。

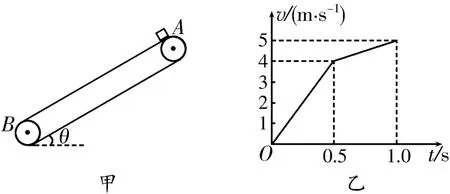
图2

(1)求物块与传送带之间的动摩擦因数μ1。

(2)求物块从A点运动到B点的过程中,传送带对物块做的功。

(3)求物块从A点运动到B点的过程中,因摩擦而产生的热量,以及物块在传送带上滑动的痕迹长度。

解析：(1)根据物块的v-t图像可知,物块在前0.5 s 时间内的加速度8 m/s2,在后0.5 s 时间内的加速度a2=根据牛顿第二定律可知,物块在前0.5 s时间内有mgsinθ+μ1mgcosθ=ma1,物块在后0.5 s 时间内有mgsinθμ1mgcosθ=ma2,解得

(2)根据v-t图像与横轴围成的图形面积表示位移可知,物块在前0.5 s时间内的位移,则摩擦力对物块做的功W1=μ1mgcosθ·x1=3 J;物块在后0.5 s时间内的位移x2==2.25 m,则摩擦力对物块做的功W2=-μ1mgcosθ·x2=-6.75 J。因此传送带对物块做的总功W=W1+W2=-3.75 J。

(3)根据物块的v-t图像可知,传送带的速率v带1=4 m/s。前0.5 s时间内传送带的位移x带1=v带1t1=2 m,因摩擦而产生的热量Q1=μ1mgcosθ·(x带1-x1)=3 J;后0.5 s时间内传送带的位移x带2=v带1t2=2 m,因摩擦而产生的热量Q2=μ1mgcosθ·(x2-x带2)=0.75 J。因此物块从A点运动到B点的过程中,因摩擦而产生的热量Q=Q1+Q2=3.75 J。前0.5 s时间内物块在传送带上滑动的痕迹长度Δx1=x带1-x1=1 m,后0.5 s时间内物块在传送带上滑动的痕迹长度Δx2=x2-x带2=0.25 m,因为Δx1＞Δx2,所以物块在传送带上滑动的痕迹长度Δx=Δx1=1 m。

(4)物块与传送带达共速前,根据牛顿第二定律得mgsinθ+μ2mgcosθ=ma3,解得a3=10 m/s2。物块与传送带达共速所用的时间物块的位移x3=,传送带的位移x带3=v带1t3=1.6 m,因摩擦而产生的热量Q＇=μ2mgcosθ·(x带3-x3)=4 J,物块对传送带做的功W1=-μ2mgcosθ·x带3=-8 J。物块与传送带达共速后,因为mgsinθ=μ2mgcosθ,所以物块与传送带一起匀速下滑,则物块对传送带做的功W2=mgsinθ· (lAB-x3),其中lAB=x1+x2=3.25 m,解得W2=12.25 J。因此全过程中物块对传送带做的功W总=W1+W2=4.25 J。

(5)t0=0.2 s时间内物块沿传送带向下做匀加速运动,根据牛顿第二定律得mgsinθ+μ3mgcosθ=ma4,解得a4=12.5 m/s2,0.2 s 末时刻物块的速度大小v4=a4t0=2.5 m/s,物块的位移0.25 m。0.2 s时刻后物块先沿传送带向下做匀减速运动,根据牛顿第二定律得μ3mgcosθ-mgsinθ=ma5,解得a5=2.5 m/s2,物块速度减小到0 所用的时间,物块的位移之后物块沿传送带向上做匀加速运动,加速度大小也为a5=2.5 m/s2,物块与传送带达共速所用的时间,物块向上的位移大小,因为mgsinθ＜μ3mgcosθ,所以物块还要做匀速运动的时间因此物块回到A端所用的时间t总=t0+t5+t6+t7=2.35 s。t0=0.2 s时间内传送带的位移x带4=v带1t0=0.8 m,物块与传送带的相对位移Δx3=x带4-x4=0.55 m;0.2 s时刻后传送带向上的位移大小x带5=v带2(t5+t6)=3.6 m,物块与传送带的相对位移Δx4=x5-x6+x带5=4.05 m。全过程中因摩擦而产生的热量Q″=μ3mgcosθ·(Δx3+Δx4)=34.5 J,电动机多消耗的电能E电=Q″+

点评:物块在0.5 s时刻后所受滑动摩擦力的方向由沿斜面向下变为向上为隐含条件,需根据物块的v-t图像中物块与传送带的速度关系判断得出。判断物块的运动性质是求解本题的关键,对于足够长传送带来说,当最大静摩擦力fmax=μmgcos θ＜mgsinθ,即μ＜tanθ时,物块在后0.5 s时间内做加速运动到达传送带底端;当最大静摩擦力fmax=μmgcosθ≥mgsinθ,即μ≥tanθ时,物块与传送带达到相同速度后将做匀速运动(受到大小等于mgsinθ的静摩擦力)到达传送带底端。(3)问中,前0.5 s时间内和后0.5 s时间内,物块相对传送带的位移方向相反,两段滑动痕迹是覆盖关系,因此痕迹总长等于两者中较大者。

三、水平二维传送带问题

例3如图3所示,生产车间有两个相互垂直且等高的水平传送带甲和乙,传送带甲的速度为v0。工件离开传送带甲前与甲的速度相同,并平稳地传到传送带乙上,工件与传送带乙之间的动摩擦因数为μ。传送带乙的宽度足够大,重力加速度为g。

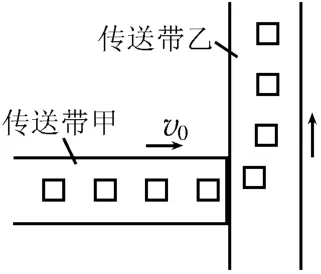
图3

(1)若传送带乙的速率也为v0,求工件在传送带乙上侧向(垂直于乙的运动方向)滑过的距离x。

(2)若传送带乙的速率为2v0,求工件在传送带乙上刚停止侧向滑动时的速率v。

(3)保持传送带乙的速率为2v0不变,当工件在传送带乙上刚停止侧向滑动时,下一个工件恰好传到传送带乙上,如此反复。若每个工件的质量均为m,除工件与传送带之间的摩擦外,其他能量损耗均不计__,求驱动传送带乙的电动机的平均输出功率。

解析：(1)以传送带乙为参考系,工件刚滑上传送带乙时有相对传送带乙的侧向速度v0和与传送带乙运动方向相反的速度v0,其合速度方向与传送带乙侧向(x轴)间的夹角α=45°,受到的摩擦力方向与合速度方向相反,摩擦力大小f=μmg,工件的速度和受力如图4所示。工件在侧向的分运动为匀减速直线运动,设侧向加速度大小为ax,根据牛顿第二定律得μmgcosα=max,解得ax=μgcosα。根据运动学公式得0-v20=-2axx,解得

图4

(2)作出工件的速度和受力如图5所示,设t=0 时刻摩擦力与侧向(x轴)间的夹角为θ,侧向、纵向加速度大小分别为ax、ay,则tanθ。在很短的时间Δt内,侧向、纵向的速度增量Δvx=axΔt,Δvy=ayΔt,解得又有tanθ=因此摩擦力方向保持不变,当vx＇=0时,vy＇=0,即工件停止侧向滑动时与传送带同速,工件的速率v=2v0。

图5

点评:求解(1)问时,理解“相对”的本质是关键,选传送带乙为参考系是准确判断工件所受摩擦力方向的基础,识别、构建工件相对传送带乙做匀减速直线运动的过程模型是简便求解的前提。求解(2)问时,工件在传送带乙上沿侧向(x轴)与纵向(y轴)滑动所用的时间相等为隐含条件,推理论证如下:在图5中,根据v0=μgcosθ·t侧,2v0=μgsinθ·t纵,tanθ=,推理得t侧=t纵。求解(3)问时,以传送带乙为参考系的解答过程更简捷,同学们不妨一试。