一道带电粒子在复合场中运动问题的多解赏析
2023-03-20华中科技大学附属中学
■华中科技大学附属中学 许 文
复合场是指电场、磁场、重力场中的两种或三种的叠加。当带电粒子在复合场中运动时,可能做匀速直线运动、匀速圆周运动、类抛体运动或一般的曲线运动等。下面以一道典型问题为例,探讨带电粒子在复合场中做一般曲线运动的几种求解方法,供大家参考。
问题:如图1所示,一质量为m,带电荷量为q(q>0)的小球(可视为质点),从足够大的水平向里,磁感应强度为B的匀场磁场中的某点由静止释放,已知重力加速度为g,不计空气阻力,求小球下落的最大高度h和运动过程中的最大速率vmax。
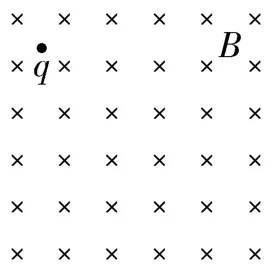
图1
分析:小球在重力作用下向下运动,当小球获得速度时,受到洛伦兹力的作用,运动方向时刻发生改变,小球做曲线运动。当小球运动到最低点时,速度方向一定水平,因此小球从开始释放运动到最低点的过程中,竖直方向上的分速度先增大后减小,当竖直分速度达到最大时,小球在竖直方向上受到的合力为零。如图2所示,设小球速度为v时,洛伦兹力竖直向上的分量Bqvx=mg,之后小球继续向下运动。因为洛伦兹力不做功,所以小球在运动过程中的机械能守恒,即小球运动到最低点时的速率最大。小球在最低点时受到的竖直向上的洛伦兹力大于重力,小球又会从最低点向右上方运动,根据机械能守恒定律可知,小球运动到与释放点等高处时速度为零,然后又重复开始的运动。
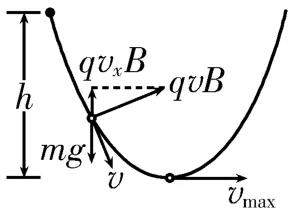
图2
解法1:利用运动的合成与分解求解。
如图3所示,小球的初速度为零,可以等效为水平向左与水平向右各有一个等大的初速度v0,令Bqv0=mg,则水平向右的速度使小球产生竖直向上的洛伦兹力与重力相平衡,小球参与一个沿水平向右速度为v0的匀速直线运动;水平向左的速度v0=使小球参与一个在竖直面内以释放点的水平线为切线且沿逆时针方向的匀速圆周运动。小球的运动可视为以上两个运动的合成。对竖直面内的匀速圆周运动有,解得R=故小球下落的最大高度在圆周的最低点,两个分运动的速度均水平向右,此时小球的速率最大,且最大速率

图3
解法2:利用动能定理与动量定理求解。小球在运动过程中受到重力和洛伦兹力作用,但只有重力做功,因此小球的机械能守恒。小球运动到最低点时速度方向一定水平,速度达最大值。在小球由静止释放运动到最低点的过程中,根据动能定理得mgh=洛伦兹力虽不做功,但产生冲量。如图4所示,将小球某一时刻的速度v分解为水平分速度vx和竖直分速度vy,其水平分速度产生的洛伦兹力竖直向上,竖直分速度产生的洛伦兹力水平向右。将小球由静止释放运动到最低点的过程分成很多微小单元,根据动量定理可知,在此过程中小球在水平方向上的动量改变量为mvmax=∑BqvyΔt=Bq∑vyΔt=Bqh。联立以上两式解得h=

图4
解法3:利用一元二次方程根的判别式求解。
小球做曲线运动,下落到最低点时的速度一定水平向右,此时小球的速度达最大,受到的洛伦兹力竖直向上。设小球运动轨迹最低点的曲率半径为ρ,根据牛顿第二定律得Bqvmax-mg=整理得+ρmg=0,此式是关于vmax的一元二次方程,因为vmax有唯一解,所以根的判别式Δ=(-ρBq)2-4ρm2g=0,解得根据动能定理得,解得
点评:解法1基于运动的合成与分解,无中生有,巧妙地将小球的初速度为零等效为两个等大反向的初速度,且令两个反向的初速度大小为适当的值,从而将小球的一般曲线运动分解为两个特殊的分运动,利用合运动与分运动的关系进行求解。这种解法思维角度巧妙,很多同学不易想到。解法2 利用动能定理与动量定理求解,在整体过程中应用动能定理,在微小过程中利用动量定理。这种解法给人一种高屋建瓴的感觉,是一种简便实用的解法。解法3巧妙地利用了一元二次方程根的判别式求解。这种解法比较特殊,是最具内涵的一种解法。
拓展:如果复合场是匀强电场、磁场、重力场三种场的叠加,那么将重力场与电场合成一个“等效场”,求出“等效重力加速度”,仍然可以用运动的合成与分解、动能定理与动量定理、一元二次方程根的判别式等方法分析求解带电粒子在复合场中做一般曲线运动的相关问题。
练一练:如图5所示,在竖直平面内有垂直于该平面向里沿水平方向的磁感应强度为B的匀强磁场。竖直平面中a、b两点在同一水平线上,相距为l。带电荷量为q>0,质量为m的质点P,以初速度v从a点对准b点射出,不计空气阻力,不考虑质点P与地面接触的可能性,重力加速度为g。
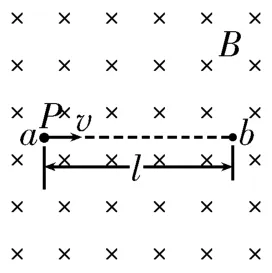
图5
(1)若无论l取什么值,均可使质点P经直线运动通过b点,则v应取什么值?
(2)若v为(1)问可取值之外的任意值,则l取哪些值,可使质点P必定经曲线运动通过b点?
(3)对每一个满足(2)问要求的l值,计算各种可能的曲线运动对应的质点P从a点运动到b点所用的时间t。
(4)对每一个满足(2)问要求的l值,质点P能否从a点由静止释放也可以通过b点? 若能,求质点P在运动过程中可达到的最大速率vmax。
参考答案:(1)v=;(2)l=(n=1,2,3,…);(3)t=(n=1,2,3,…);(4)能,vmax=。
