超临界氮气在规则球床堆中的流动与传热特性分析
2023-03-20陈煜尧童念雪陈亚春魏健健张德志
陈煜尧 程 帅 童念雪 陈亚春 魏健健 张德志 金 滔
(1 浙江大学制冷与低温研究所 杭州 310027)
(2 浙江省制冷与低温技术重点实验室 杭州 310027)
(3 西北核技术研究所 西安 710024)
1 引言
近临界态流体的热物性在类临界点变化剧烈,流体物性一旦超过临界点,一种无结构的、均匀的、连续的超临界流体在状态空间中普遍存在。由于超临界流体的独特物性,近年来在多孔介质换热、高温气冷堆、催化反应器、蒸汽循环发电等领域备受青睐。
在某复热型高温高压气体制备系统实验平台中,需要产出压力2—15 MPa,温度0—450 ℃的气体。常规的工业管路换热系统,受限于系统的加压、加热和输运能力,难以实现快速产气、充气的目标。Osofsky 等[1]研制了液氮复热式高温高压气体制备系统,用于提供稳定可靠驱动气体且实现对生产过程的有效调控。系统中采用卵石堆积床作为复热部件,堆积床的致密堆积结构能够有效加强气固元件间的换热,流体与堆积颗粒换热越充分,越有助于后期的温度精准调控。高压条件下超临界流体在堆积床内的复杂流动换热特性决定着堆积床内温度分布,会影响堆积床的设计、性能乃至安全运行。
为了解堆积床中流体的复杂流动特性,相关学者针对堆积床流动传热过程开展了大量实验研究。Ergun等[2]对空气、氮气、二氧化碳等不同流体工质流经固体颗粒堆积床的实验结果进行了详细的讨论,给出经典的固定床压降经验关联式(Ergun equation),关联式表明,压降与表面速度之比是质量流量的线性函数,关联式的系数取决于固定床孔隙率、流体与颗粒接触的表面积和流体粘度,但该压降公式仅适用于低雷诺数工况(Re<1 000)。Kerntechnischer 等[3]通过实验提出了著名的压降预测关联式(KTA equation),该式适用于更高雷诺数范围(Re/(1-ε) <105)的气冷固定床反应器。传统的堆积床试验研究成本高、局限性大,难以测量堆积床内流动参数,因此,国内外相关学者开始寻找合适的堆积床流动换热数值计算方法。Ahmadi 等[5]基于CFD 数值模拟方法,研究了流速、堆积球尺寸对超临界水在单一尺寸堆积球床内流动压降的影响,并拟合出Re在1.5 × 104—1.5 ×106范围的压降公式。国内学者也陆续提出利用规则排列结构来简化堆积床的策略[6-8],清华大学基于规则堆积床提出模块式堆积床的设计方案[7-8],发现规则球堆积床的流动阻力明显低于随机床,有助于获得更强的综合换热性能。然而,由于堆积结构的复杂性,现有研究大多采用简化的周期性球床模型[6],难以直接得到球床内流动换热细节及球床瞬态温度、压力求解结果;此外,对于超临界氮气作为流体工质的堆积床CFD 研究还不多见。
本研究利用规则球堆积床模型对超临界氮气在堆积床中的流动及传热特性进行模拟分析,观察堆积床内瞬态温度、压力等典型参数分布,同时研究液氮流量、颗粒直径和堆积床高径比等因素对堆积床综合性能的影响,为液氮复热型高温高压气体制备系统中堆积床的优化设计打下基础。
2 模型与计算方法
2.1 物理模型及网格划分
球床堆结构复杂直接建模得到的CFD 模型计算量巨大,为提高计算的时效性,根据液氮复热型高温高压气体制备系统中的堆积床建立如图1a 所示的二维旋转轴对称模型。堆积床尺寸为:总高度3.1 m(上段缓流区0.6 m,中间填充区2.0 m,下段缓流区0.5 m),直径0.85 m;堆积床孔隙率0.4,堆积单元体直径12 mm,单元体间距13.5 mm,上下颗粒层交替排列。文献[9]证明了该排列具有基本对称单元体积较小、流道间无直通孔的优点。
规则排布堆积床生成的结构化网格及局部网格如图1b 所示。对模型进行网格独立性检验,为兼顾计算结果准确性与计算时效,在网格数为1.9 ×106的基础上继续加密网格,充分考虑流固耦合计算域边界层网格数量对模拟结果的影响。对于不同网格数量的模型,监测X=0.7 m 截面处的氮气平均温度随时间的变化。由图2 可知,网格2 与网格3、网格4 对应的温度变化曲线近似重合,因此选取网格数为1.9 ×106的模型进行模拟求解。

图1 堆积床物理模型及网格划分Fig.1 Physical model and meshing of pebble bed

图2 网格无关性验证Fig.2 Grid independent verification
2.2 数值模型
模拟中考虑重力因素对流体换热的影响,其连续性、动量及能量守恒方程分别为:
式中:ρ为流体密度,kg/m3;为流体速度矢量,m/s;P为压力,Pa;t为时间,s;T为温度,K;为重力加速度,m/s2;为应力张量,Pa;为外部体积力,N/m3;λ为有效导热系数,W/m·K;cp为定压比热容,kJ/(kg·K);SE为体积热源项,kJ。
基于Fluent 软件对氮气在堆积床内的流动传热情况进行模拟计算,采用Coupled 代数算法计算速度压力耦合场,选择标准壁面函数和RNGk-ε湍流模型;为了提高控制方程精度,压力、动量和能量方程采用二阶迎风格式;求解中能量松弛因子设置0.8,动量松弛因子0.7,其它按默认值设置;数值计算的收敛性判据采用连续性和动量方程相对残差小于10-4,能量方程变量相对残差小于10-6,总换热时间设定为300 s,最小迭代时间步长0.005 s。
2.3 边界条件
Fluent 数值计算中,定义液氮入口边界为质量流量入口,质量流量为1.8 kg/s,温度为77 K;定义氮气出口边界为压力出口,压力为15 MPa;中心轴线定义为旋转对称轴,堆积床内高温填充球与流体接触面为耦合传热壁面,其余为绝热壁面边界。超临界状态下氮气的密度、比热容等物性随温度变化明显,类临界点处存在物性突变,为准确反映物性剧烈变化对流动换热的影响,流体材料物性采用分段拟合的方式。由于流体处于超临界态时,流体蒸发潜热和表面张力消失,相变不再发生,因此,超临界氮流动传热数值模拟仍采用单相流体流动传热的计算方法[10]。
2.4 模型验证
为验证本文数值模拟方法的可靠性及结果的准确性,针对Cails 等[11]和Romkes 等[12]进行的空气冷却单排球的实验装置进行具体参数建模,基于Fluent软件进行数值模拟,并将模拟结果与实验值对比分析,如图3 所示。由图可知,规则球床堆摩擦系数与努塞尔数在小雷诺数范围内,模拟结果与实验结果误差较小,说明本文的模拟方法对流体流经堆积床流动换热特性的研究具有可行性。

图3 规则球床堆气体流动阻力系数与努塞尔数验证Fig.3 Verification of gas flow resistance coefficient and Nusselt number in regular pebble bed
3 模拟结果及分析
当系统运行压力为15 MPa、入口液氮质量流量为1.8 kg/s 时,不同时刻堆积床内温度分布如图4 所示。由图可知,随着液氮不断充入堆积床,低温氮气与高温堆积球换热带走热量,床内热容量不断降低。由局部流场图可以看出,小球通道间距骤缩处流速较高,在相邻小球间存在局部高温区。这是由于背流区流动处于接近滞止状态,背流区热量难以通过流动带走导致传热恶化,故呈现出流体局部高温区。下文着重探讨入口流量、固体颗粒直径和填充区域高径比对超临界氮气在堆积床内流动传热特性的影响情况。
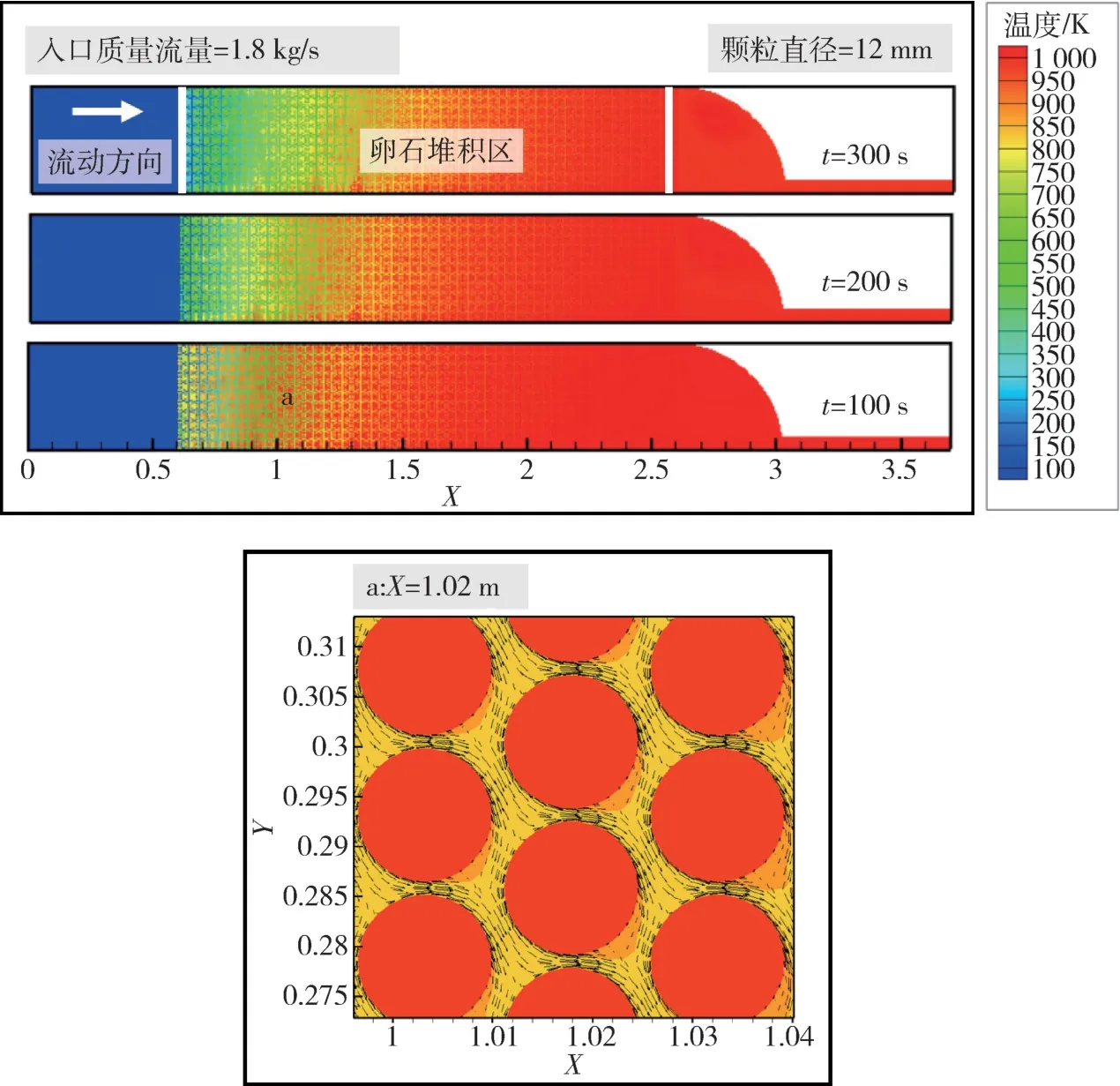
图4 不同时刻堆积床内温度场分布及局部流场图Fig.4 Temperature field distribution and local flow field diagram in pebble bed at different time
3.1 入口流量的影响
堆积床内综合换热性能与流体工质流量大小紧密相关,数值模拟选取入口流量范围0.5 —36 kg/s(对应Re范围:100—10 000)。图5 为填充区域平均压降与平均对流传热系数随入口流量变化图。由图5可知,随着Re的增加,堆积床内平均压降显著提升;当Re在100—1 000 范围内,对应液氮入口质量流量0.5—3.6 kg/s,涵盖了液氮复热型高温高压气体制备系统所有工况,此时,堆积床内平均压降模拟值在17—600 Pa/m 之间,平均对流传热系数在10.2—32.6 W/m2·K 之间。此外,堆积床局部传热系数也随Re的增大而增大,这是由于床内氮气平均流速随流量增大而上升,增强了氮气与颗粒间的对流换热强度。

图5 平均压降及平均换热系数随入口流量的变化Fig.5 Change of average pressure drop and heat transfer coefficient with inlet flow
3.2 颗粒直径的影响
填充区域的固体颗粒是复热型堆积床的核心供热元件,不同规格的颗粒直接影响堆积床的阻力特征及传热性能。表1 给出不同颗粒直径对应堆积床结构参数。堆积床出口温度及平均压降随颗粒直径变化情况如图6 所示。由图可知,堆积床出口温度随颗粒直径变化剧烈,当颗粒直径增大,流体与颗粒接触的比表面积会降低,导致相氮气与颗粒的换热减少,因而相同换热时间内,堆积床出口氮气温度会显著降低。此外,由图7 给出的排气温度随时间变化具体数据可知,当颗粒直径为30 mm 时,300 s 换热时间后,堆积床出口温度已经低于目标充气温度723.15 K;对于压力分布规律,填充区域的压降随颗粒直径增大而减小,当颗粒直径增大到30 mm 时,对应平均压降为32 Pa/m,继续增大颗粒直径,堆积区域阻力下降趋于平缓,因而对床内平均压降的影响越来越小。综合堆积床排气温度及阻力特性,小直径固体颗粒在提升堆积床阻力的同时有利于增强和流体间的传热。在满足排气温度的基础上,可选用较大直径的固体颗粒,降低流体流动阻力。

表1 不同颗粒直径对应堆积床结构参数Table 1 Structure parameters of pebble bed corresponding to different particle diameters

图6 出口温度与平均压降随颗粒直径的变化Fig.6 Change of outlet temperature and pressure drop with particle diameter

图7 不同颗粒直径对应出口温度随时间的变化Fig.7 Change of outlet temperature with time for different particle diameters
3.3 堆积床高径比的影响
堆积床结构尺寸直接影响气体制备系统的占地面积及布置方案,分析高径比对流动传热的影响对堆积床设计具有重要意义。表2 给出不同长径比下堆积床结构参数。图8 为堆积床出口温度和平均压降随高径比变化规律,可以看出,排气温度和平均压降随高径比的增大而增大,这是由于氮气在堆积床流动过程中,所产生的轴向阻力对氮气运动的削弱作用大于径向阻力对氮气的削弱作用,随着高径比的增加,氮气在堆积床中的轴向流动阻力占比增大,因而单位长度平均压降不断升高。当流动阻力增大,单位时间内氮气与堆芯换热更加充分,堆积床出口温度也逐渐升高。

表2 不同高径比对应堆积床结构参数Table 2 Structure parameters of pebble bed corresponding to different ratio of height to diameter

图8 出口温度及平均压降随高径比的变化Fig.8 Change of outlet temperature and pressure drop with ratio of height to diameter
图9 为不同高径比下堆积床出口温度随时间变化曲线,该图更加直观的反映了大高径比堆积床在相同时间内流体换热更加充分。在高径比为5 时,排气温度可高达918 K,在高径比为1 时,排气温度仅为698 K。因此对于堆积床外形尺寸设计,需要协同考虑堆积床换热强度、堆积床压降阻力大力,应在满足排气温度的基础上,选用小高径比结构的堆积床,降低超临界氮气流动阻力。

图9 不同高径比对应出口温度随时间的变化Fig.9 Change of outlet temperature with time for different height to diameter ratio
4 结论
本研究基于Fluent 软件对液氮复热型高温高压气体制备系统中超临界氮气在规则球床堆内的流动换热进行了模拟分析,着重探讨了入口流量、颗粒直径和高径比对超临界氮在堆积床内流动换热特性的影响规律,结论如下:
(1)对于规则球床堆,超临界氮气与床内固体颗粒平均换热强度随入口流量的增加有显著提升;然而填充区域平均压降也会随入口流量的增加而变大,当堆积床入口流量在0.5—3.6 kg/s 范围内,床内平均压降最高可达600 Pa/m。
(2)小直径固体颗粒有利于增强流体和堆积床的传热,当颗粒直径为18 mm 时,堆积床出口温度远高于目标充气温度。对于压力分布规律,填充区域的压降随颗粒直径增大而减小,当颗粒直径增大到30 mm时,对应平均压降为32 Pa/m,继续增大颗粒直径,填充区域阻力下降趋于平缓。
(3)对于不同高径比的规则堆积床,高径比越大,单位时间内超临界氮气与堆芯换热更加充分,堆积床出口温度随着升高,在高径比为5 时,排气温度可达918 K。随着高径比的增加,超临界氮气在床内的轴向流动阻力也会增大,填充区域的压降成倍数增长。
