超临界碳氢燃料在圆/矩形管内流动传热数值研究
2023-03-20赵金辉孔清杰魏延龙布一凡
赵金辉 孔清杰 魏延龙 布一凡
(郑州大学机械与动力工程学院 郑州 450000)
1 引言
在超音速飞行时,飞行器上的空气温度过高,超燃冲压发动机无法有效冷却,因此有必要将发动机燃料用作冷却剂,来实现再生冷却循环系统[1]。即在燃料进入燃烧室之前,先将其用作冷却剂吸收机体的热量。碳氢燃料如火箭推进剂3 号(rocket propellant-3,简称RP-3)是目前常用的冲压发动机燃料。再生冷却循环系统中,冷却通道内的压力通常会超过RP-3的临界压力。超临界压力下,流体的热物性会随着温度的变化而出现很大的波动,严重的还会导致传热恶化。
Li 等[2]采用强化壁面处理的RNGk-ε湍流模型,研究了RP-3 在超临界压力下的传热特性。发现当壁面温度超过初始加热段的拟临界温度时,传热并没有增强,反而减弱。当壁温接近拟临界温度时,发生传热恶化。Hitch 等[3]研究了流体湍流程度对超临界压力下碳氢燃料在竖直圆管内换热过程。在压力大于非湍流条件下临界压力的两倍时,局部传热系数下降为强制对流值的1/5 倍。这种情况可能导致冷却部件的壁温大幅升高。Gu 等[4]和Tao 等[5]研究了超临界压力下水平圆管内碳氢燃料对流换热特性,发现在均匀热流的条件下,拟临界温度附近流体热物性发生了显著变化,产生较大的压力梯度,湍流强度减弱,导致壁面和流体之间的换热能力下降。贾洲侠等[6]分析了热流密度、进口雷诺数对超临界下RP-3 在水平圆管内的对流换热的影响。表明了沿流动方向,管内表面传热系数随热流密度的增大先减小后增大;在低进口温度及低进口雷诺数情况下,换热均出现先恶化后强化的现象。
Pizzarelli 等[7]和Ruan 等[8]等模拟了超临界压力下矩形冷却通道内低温甲烷对流换热,发现在拟临界温度和超临界压力下,高壁面热流密度时,急剧的流体热物性变化会导致传热恶化和壁温迅速升高。Pizzarelli[9]针对4 种不同矩形冷却通道内超临界甲烷的流动进行了数值研究,发现高宽比会对传热恶化发生时的强度、位置产生影响。王彦红等[10]和李素芬等[11]对单壁面加热的方形通道内超临界碳氢燃料进行了数值研究。拟合得到了传热恶化的临界热流密度和壁温关系式。在超临界压力下,较低的热流密度、增大压力、降低进口流体温度或提高质量流速均可以改善传热。
文献[12]提出10 组分替代模型,用于计算传热分析所需的热力学和输运性质。文献[13]实验证明10 组分替代模型具有较高精度。对于超临界RP-3的流动传热研究,主要集中于圆形和矩形通道内,对于在这两种通道内传热特性的对比研究较少。本课题研究了圆形、矩形冷却通道内超临界RP-3 对流换热特性并对不同形状冷却通道内的对流换热能力作了对比。RP-3 航空煤油热物性参数采用了文献[12]提出的10 组分替代模型。
2 数值计算模型与方法
2.1 几何模型
图1 为本研究模拟的非对称受热下超燃冲压发动机冷却通道模型。外部固体边界为4 mm ×4 mm矩形,流道截面形状分别为圆形、矩形,几何参数如图2。通道总长400 mm,加热段长度为280 mm,入口前设置120 mm 的绝热段,以提供充分发展的湍流,减小入口效应影响。
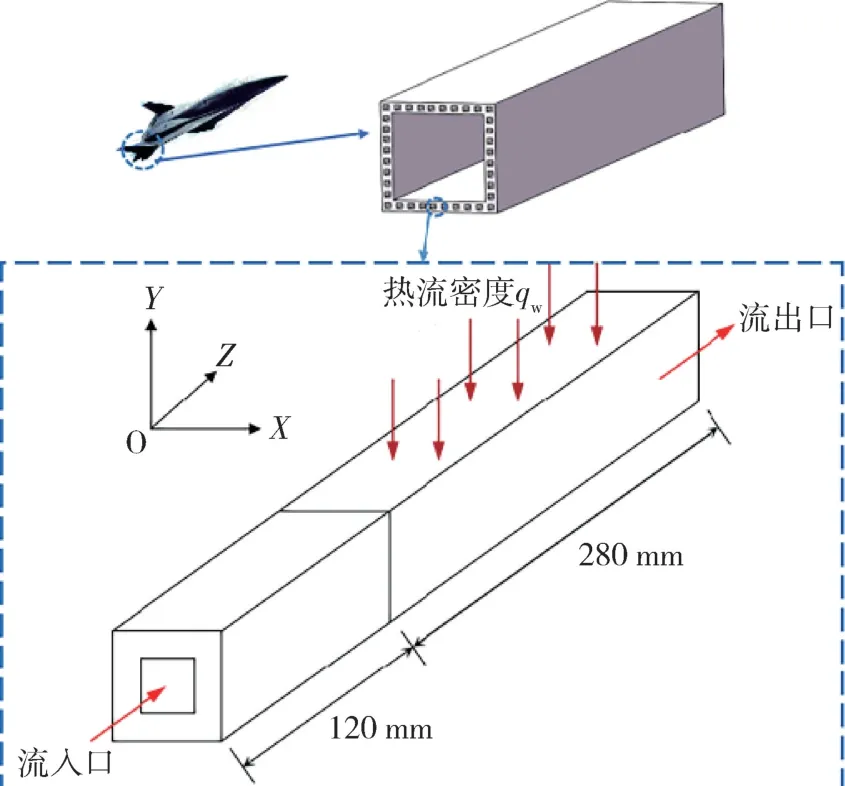
图1 冷却通道模型Fig.1 Cooling channel model
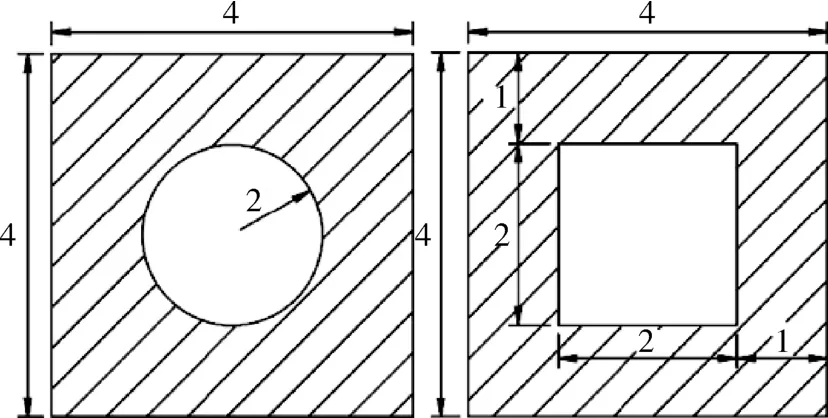
图2 冷却通道横截面(mm)Fig.2 Cross-sectional view of cooling channel(mm)
2.2 边界条件及控制方程
计算模型选用RNGk-ε两方程湍流模型和强化壁面函数处理方法进行湍流分析;通道壁面设定为无滑移边界条件,采用基于压力-速度耦合方程的SIMPLE 算法进行求解计算,对流项和扩散项采用二阶迎风离散格式。
压力4 MPa 时RP-3 热物性随温度变化曲线如图3 所示。将给定压力下的超临界碳氢燃料密度、导热系数、定压比热容、粘度随温度变化曲线拟合成分段线性函数进行数值模拟计算。超临界压力下,冷却通道内RP-3 的热物性参数可认为是温度的单值函数。
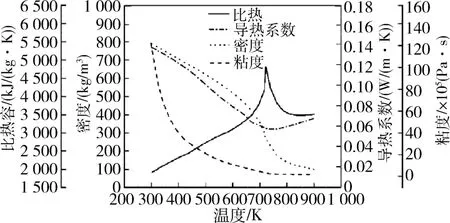
图3 压力4 MPa 时RP-3 热物性随温度变化曲线Fig.3 Thermophysical properties of RP-3 at pressure of 4 MPa
计算工况:出口设置为压力出口,恒定压力P=4 MPa;入口边界条件为质量通量入口:入口温度Tin=400 K,入口质量通量G=500 kg/(m2·s);固体材料导热系数视为常数,且导热系数λ=20 W/(m·K);YOZ平面为对称面边界条件;上壁面为壁面加热边界条件,热流密度qw=2.0 MW/m2,满足以下方程:
质量守恒方程(6)、动量守恒方程(7)、能量守恒方程(8)以及湍流方程(9)(10)如下:
式中:u为速度,ui、uj、uk:各坐标轴方向的速度分量,m/s;q为热流密度,W/m2;p为压力,Pa;y为网格单元中心到壁面的垂直距离,mm;lε为含能涡的特征长度;κ为Karman 数,壁面光滑时取0.4;Rey为湍流雷诺数;ρ为流体密度,kg/m3;τ为黏性应力项,Pa;et为流体总内能,J;λ为固体导热系数,W/(m·K);T为温度,K;t为时间,s;Prk、:Prε为湍流普朗特数,取值均为1.39;k为湍动能;ε为湍动能耗散率;Gk为由平均速度梯度所引起的湍动能的产生项;μ为黏性系数,N·s/m2;μeff为有效黏度;Cμ为模型系数,取0.084 5;为模型常数。
2.3 网格独立性分析
矩形、圆形通道数值模型具有一定的相似性,此处仅针对矩形冷却通道进行网格独立性分析。图4为不同网格数量下出口平均温度、进口平均压力变化曲线。在保证精度的同时兼顾计算效率,选取网格参数为120 W 的数值模型进行后续研究。
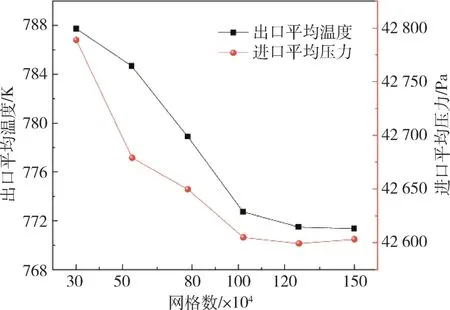
图4 网格独立性Fig.4 Grid independence
2.4 数值方法验证
文献[14]提出矩形、圆形通道内具有相似的对流换热特性,可以采用相同的湍流模型和数值方法。为验证本研究选用的RP-3 航空煤油热物性、湍流模型及数值方法的可靠性,基于文献[15]中水平矩形通道内超临界RP-3 的对流换热试验进行数值模拟。从图5 看出,模拟计算结果与实验结果吻合度较高,最大误差8.1%。

图5 数值模拟与实验结果对比Fig.5 Comparison of numerical simulation and experimental results
3 模拟结果与讨论
3.1 圆形冷却通道对流传热特性
给定计算工况下,圆形通道内出现传热恶化。图6 为圆形通道在YOZ截面上的温度、速度分布。壁面温度并不随着流动进行单向增加,在z=180—280 mm范围内,上、下壁面均出现温度峰值。此现象与超临界RP-3 的热物性有关,超临界压力下RP-3 的导热系数随着温度升高而减小,换热效果变差,造成壁温快速升高。因此在z=180—280 mm 内,壁温出现峰值。轴向截面上形成了“M”形速度等值线,这是由于近壁区域流体密度减小导致速度大于主流区域流体的速度。在“M”形速度等值线中,近壁面区域流体的速度梯度为零,流体湍流扩散能力下降,从而减小了对流传热,出现传热恶化。

图6 YOZ 截面温度和速度分布Fig.6 Temperature and velocity distribution of YOZ section
图7 为XOY截面沿流向温度和速度分布。由于固体导热系数较小,热流密度一定,上壁面和侧壁面在y轴方向存在较大的温度梯度。流体温度沿流动方向不断上升,由于近壁面处的流体先参与到换热过程中,温度在径向上呈现四周高、中间低的特点,近壁面处流体具有较大的温度梯度。流体温度的分布特征表明:光滑圆管内,流体的湍流程度较低,很大程度上依靠热传导进行换热。受流动边界层的影响,各截面内流体速度呈现中间最高,向四周速度逐渐降低。流体的速度沿流动方向逐渐增大,这是因为流动过程中流体温度升高、密度减小,导致相同质量流量下流体的流速变高。
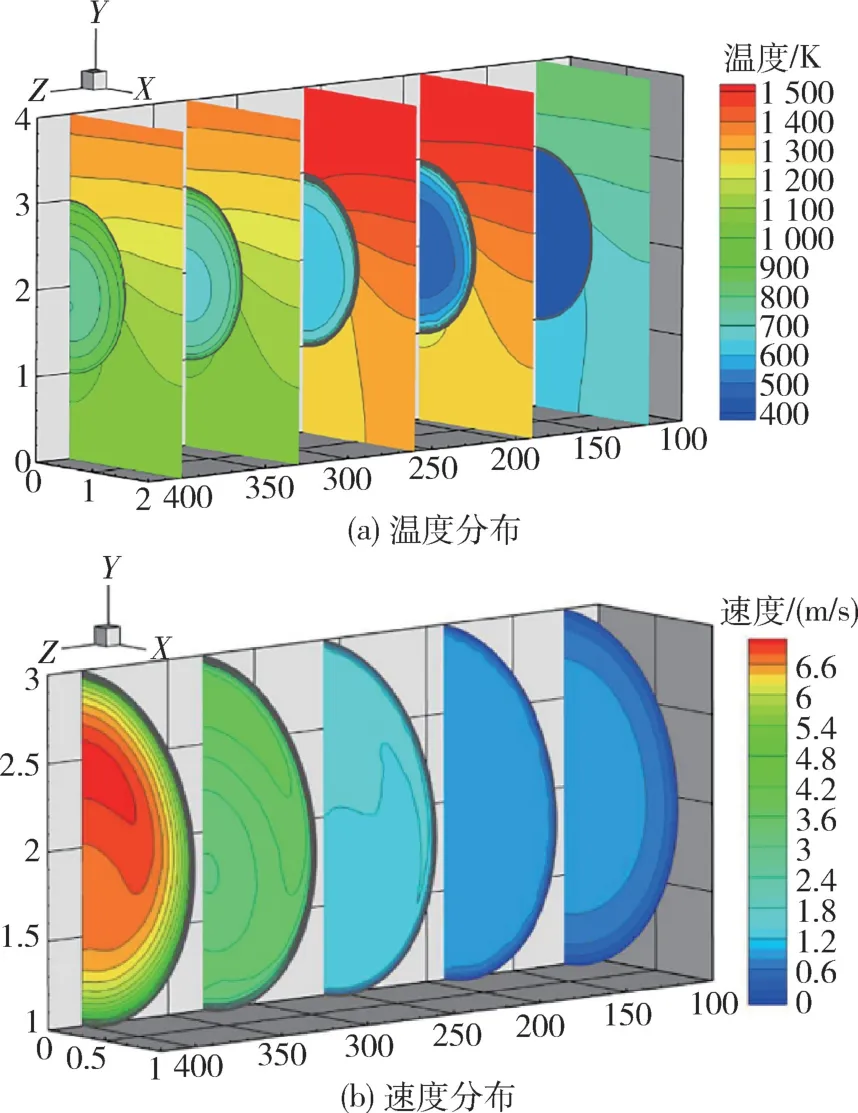
图7 XOY 截面温度和主流速度分布Fig.7 Temperature and velocity distribution in XOY section
3.2 矩形冷却通道对流传热特性
图8 显示了矩形冷却通道在YOZ截面的温度、速度、比定压热容(cp)分布图。图8a,8b 可以看出,在z=170—270 mm 之间,加热上下壁面均出现壁温峰值。上下壁面出现了零速度梯度区域,速度等值线由抛物线型转变为“M”形速度等值线。矩形冷却通道内壁温峰值和“M”形速度等值线的出现位置较之圆形均有所提前。图8c 可以看出,矩形冷却通道与圆形类似,近壁面处流体参与换热后温度升高,流体的密度在径向存在很大的梯度。随着流动的继续,近壁面流体的比定压热容率先剧烈升高,此时近壁处流体温升变慢,近壁区流体与核心区域流体的温差减小,流体之间的对流换热能力恢复。在z=380 mm,主流区域的流体比定压热容达到了峰值,流体进入超临界状态。

图8 YOZ 截面温度、速度、cp 分布图Fig.8 Temperature,velocity and cp distribution in YOZ section
图9 显示了在XOY截面下z=370 mm 处的温度、比定压热容(cp)分布云图。由于固体材料较小的导热系数,固体壁面中存在明显的温度梯度,且由于单面加热,温度梯度从上壁面到下壁面逐渐减小。图9a 中黑框标记的为流体的拟临界温度等值线。在z=370 mm 处,冷却通道内大部分区域流体均达到超临界状态,仅中心区域流体温度仍低于拟临界温度。图9b 中黑框标出了cp/cp,max=99%的等值线,cp,max处在两条等值线之间。靠近壁面的流体温度高于拟临界温度,靠近主流中心的流体温度低于拟临界温度。当流体温度低于拟临界温度,cp随温度的升高而升高,在拟临界温度附近时,cp达到峰值;当流体温度高于拟临界温度进入超临界状态,cp会随着温度的继续升高先减小再增大。与文献[11]中超临界RP-3 的热物性相符。比定压热容的这种变化趋势在图中体现,等值线外侧的流体向壁面方向cp先减小再增加,此时近壁面处流体的cp较高。
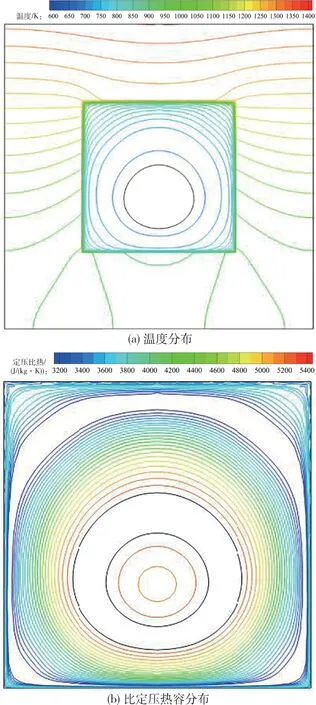
图9 z=370 mm 截面处温度、cp 分布图Fig.9 Temperature and cp distribution at z=370 mm
4 对流传热特性的对比
两种形状冷却通道的水力直径Dh、计算工况及对应参数如表1。保持入口质量通量、温度不变,入口处的雷诺数仅与冷却通道的水力直径有关。

表1 水力直径与计算工况参数Table 1 Hydraulic diameter and calculation parameters working
4.1 主流速度沿程变化
图10 为两种流道形状的通道内,无量纲速度(u/uin)的沿程变化。发现:(1)u/ uin均沿流动方向增大,这是因为流体密度随着温度的升高不断减小,在流量不变的情况下速度变大;(2)圆形冷却通道内u/uin始终大于矩形,原因是矩形通道内有“角区”的存在,导致对附近流体流动有阻塞作用;(3)圆形冷却通道内流体无量纲速度上升更快且出口流速更高。
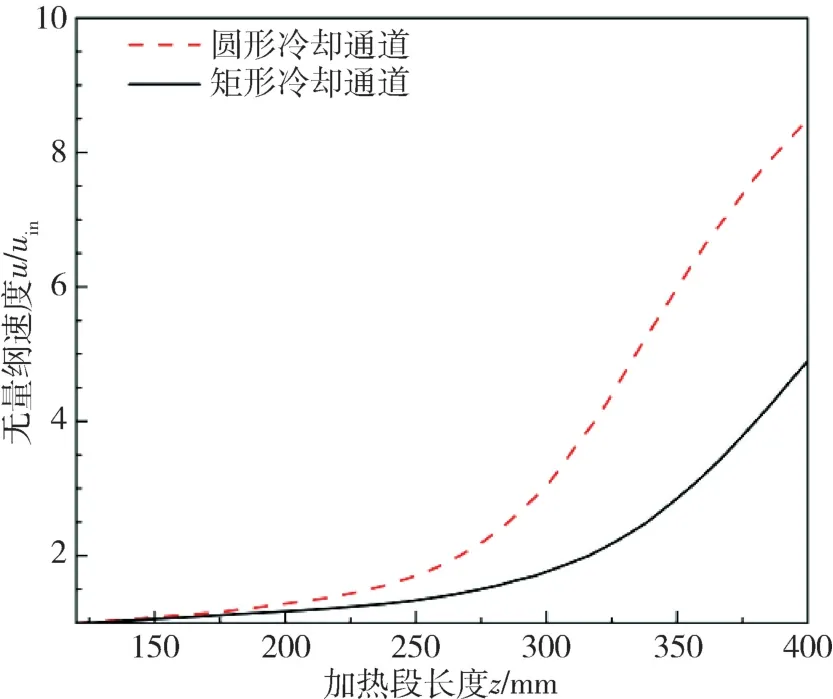
图10 沿程u/uin变化曲线Fig.10 u/uin curve along z
4.2 上壁面温度、流体温度对比
图11 为沿流向方向,上壁面及流体平均温度的变化趋势。(1)流体平均温度均沿流向升高,在加热段入口附近,圆形冷却通道内流体的温升速度快于矩形;在加热段后半段,两种冷却通道内流体温升速度相差不大。(2)圆形比矩形冷却通道的出口处流体平均温度高67 K。(3)圆形冷却通道上壁面温度峰值大于矩形且峰值温差为150 K。圆形冷却通道的上壁面平均温度在z=120—180 mm 处迅速升高,随后又急速下降,在z=320 mm 左右下降到矩形冷却通道以下。圆形冷却通道的上壁温峰值更靠近加热段入口处。矩形冷却通道上壁面温度曲线在加热段入口处缓慢上升,随后在z=170—270 mm 处附近到达峰值后缓慢下降。
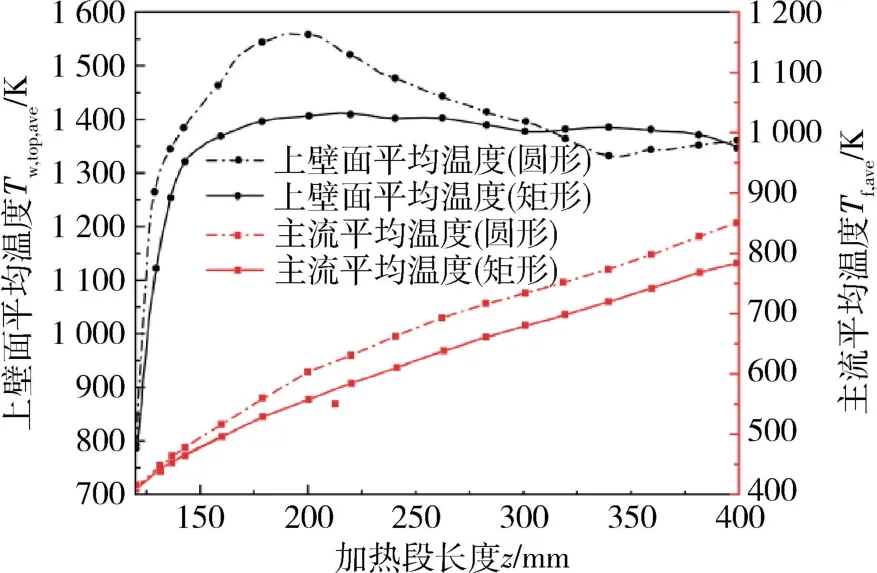
图11 上壁面及主流沿程平均温度Fig.11 Top wall and fluid average temperature along z
4.3 沿程平均换热系数和平均努塞尔数的对比
图12 为沿程平均对流换热系数和无量纲努塞尔数(Nu/Nuin)的变化曲线。对比发现圆形通道内沿程平均对流换热系数在加热段入口处缓慢升高,在z=260 mm 处附近,平均对流换热系数迅速变大,在出口处增速放缓。平均无量纲Nu数沿程变化趋势与平均对流换热系数一致;z>280 mm 后,圆形通道内无量纲Nu数显著高于矩形,表明圆形通道沿流动方向对流换热能力更强。
5 结论
本研究对不同截面形状的冷却通道内超临界压力下RP-3 的对流换热特性进行了模拟研究。所得结论如下:
(1)圆形冷却通道内传热恶化的发生是由于近壁流体温度率先达到拟临界温度时,密度剧烈下降出现零速度梯度区所致。传热恶化发生时,YOZ截面上的速度场中出现“M”形速度等值线。
(2)在矩形冷却通道内,也会发生传热恶化,核心区域流体在z=380 mm 处主流流体转变为超临界状态,在z=370 mm 径向截面上的拟临界温度、拟临界密度、拟临界比定压热容等值线出现在核心主流区。
(3)在相同的工况条件下发现相比矩形冷却通道,圆形冷却通道流体出口平均温度更高,无量纲速度更大,且上壁温的峰值比矩形高150 K。进一步对比沿程平均对流换热系数和平均无量纲Nu数发现:超临界压力下,在z>280 mm 后,圆形通道内平均对流换热系数和平均无量纲Nu数显著高于矩形,表明圆形通道内沿流动方向对流换热能力更强,冷却效果优于矩形。
