大型结冰风洞制冷系统蒸发压力预测与降温过程优化研究

张平涛 王文瑄 郭向东 吕宏宇 陈 良 侯 予

(1 中国空气动力研究与发展中心结冰与防除冰重点实验室 绵阳 621000)

(2 西安交通大学能源与动力工程学院 西安 710049)

1 引言

作为飞行器结冰与防除冰试验研究的基础设施平台,大型结冰风洞是中国航空工业发展的重要保障。制冷系统是结冰风洞的重要组成部分,通过热交换器冷却气流为试验提供低温环境。中国已建成的大型结冰风洞用液氨直接蒸发制冷,风洞气流场温度主要取决于液氨蒸发压力和流量[1]。液氨由多台定频泵从低压循环桶供给至风洞蒸发器,液氨流量通过氨泵启停实现分级调节,液氨蒸发压力的控制是风洞气流场温度及制冷系统负荷调节的关键,与低压循环桶压力相关。为了满足飞行器不同试验工况要求,需要在试验过程中对制冷系统蒸发压力进行快速预测,实现风洞气流场温度快速准确调节和系统能耗降低。

目前,大型制冷系统控制参数预测方法已在大型空调系统等应用领域得到了充分研究。Kusiak 等人[2]通过动态神经网络算法建立了空调系统的能耗预测模型,优化供气温度和压力设定值,与传统的控制策略相比,所提出的模型节省了高达30%的能耗。王炳文[3]以夏热冬暖地区某商场中央空调冷源系统为研究对象,以大量冷源系统实际运行数据为驱动,提出了冷源系统运行参数优化的数据挖掘方法。周璇[4]提出基于支持向量回归机的空调逐时负荷滚动预测算法,解决空调系统节能优化控制的问题。Wei Xiupeng[5]等提出一种数据驱动的方法,用于优化HVAC 系统的总能耗。Zeng Yaohui[6]等建立了典型气象年气象参数条件下某办公建筑的逐时冷负荷的支持向量机和BP 神经网络预测模型,比较了两种模型的预测精度。上述研究表明人工智能算法建立制冷系统运行预测模型是进行制冷系统运行优化的有效手段,现有研究主要针对大型空调系统开展,而大型结冰风洞制冷系统制冷温度跨度更大、负荷变化更加剧烈,需要针对风洞试验工况要求,进一步结合热力学仿真开展主要控制参数快速预测方法研究。本研究建立了制冷系统蒸发压力热力学预测模型,结合BP 神经网络方法实现了不同蒸发器出口气流温度、试验模拟高度、试验风速等试验参数下的低压循环桶蒸发压力快速预测。

2 制冷系统蒸发压力热力学预测模型

2.1 蒸发器模型控制方程

本研究的大型结冰风洞系统流程图如图1 所示。针对热交换器部分,建立一维流动换热模型,连续方程、能量方程和压降计算方程分别为[7-8]:

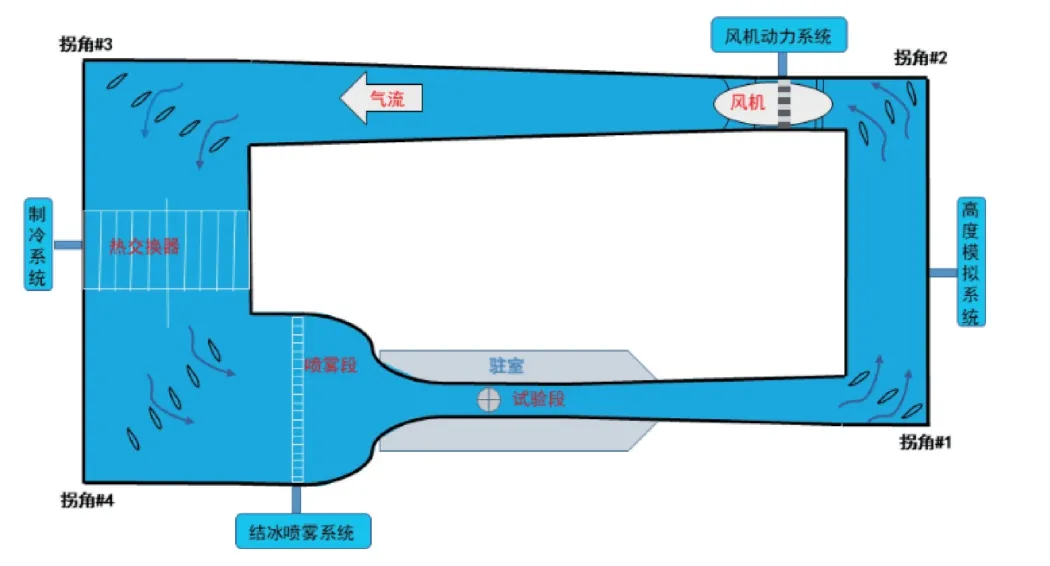
图1 大型结冰风洞系统流程图Fig.1 Schematic of an icing wind tunnel system

式中:ρ为换热流体密度,kg/m3;u为流体平均速度,m/s;ϕ为单位换热量,W/m3;h为焓值,J/kg。换热流体与管壁间的热流密度以及压降使用传热关联式进行计算。

换热器低温管路两相流动传热计算包括压降特性与换热特性[6,9]。在压降计算部分,由于本研究在风洞试验温度范围内氨气液粘度比值均小于35。根据Whalley[10]所提出的当μL/μG<1 000 时,使用Friedel 关联式所提出的分相模型[11],研究中首先计算单相流体的压降,然后通过液相系数修正因子计算两相压降。

式中:Δpf为压降,kPa;L为流过的管道长度,m;为液相系数;A1、A2和A3为两相影响因子;x为干度;μ为动力粘度,Pa·s;下标L 为液相,G 为液相质量流量,(kg/m2·s)。

采用Blasius 公式计算换热器管内氨液紊流流动对应的单相摩擦因子。采用叠加法(Chen’s model[12])进行管内两相流动传热系数计算。在管内流动沸腾的情况下,核态沸腾部分的传热系数(S)被抑制,而对流蒸发的传热系数(E)被加强。

式中:hL由Dittus-Boelter 公式计算,hNB由Copper 方程式计算。

大型换热器的高度落差造成各模块入口氨液过冷度不同,高度落差越大过冷度越大。在这种情况下,需要考虑管内液体单相流动换热的情况,单相流动摩擦因子和换热系数与上述叠加法中的单相部分计算方法一致,即分别由Blasius 公式和Dittus-Boelter公式计算。

2.2 传热器空气侧流动传热计算关联式

空气侧为强制对流换热,可按照翅片管式换热器空气侧流动公式进行计算[13],其中摩擦压降的计算公式为:

式中:Fp为翅片间距,m;Pt为翅片横向间距,m;Pl为翅片纵向间距,m;dc为空气侧水力直径,m;Redc为空气侧雷诺数。

传热系数计算方面还需要考虑翅片对换热的强化作用[14]。

式中:ηo为强化因子,j为换热因子,Dh为空气侧水力直径,m;N为管排数。强化因子计算详见文献[14]。

2.3 模型验证

图2a 中针对10 组试验工况,利用制冷系统蒸发压力热力学模型进行低压循环桶压力预测,使用试验数据进行模型验证。结果表明低压循环桶压力预测值与试验数据均方根偏差为0.08 ×105Pa,最大偏差为0.13 ×105Pa。将3 组工况的仿真模型结果与降温试验数据进行对比,模拟降温趋势与试验降温趋势符合,对比结果如图2b 所示。

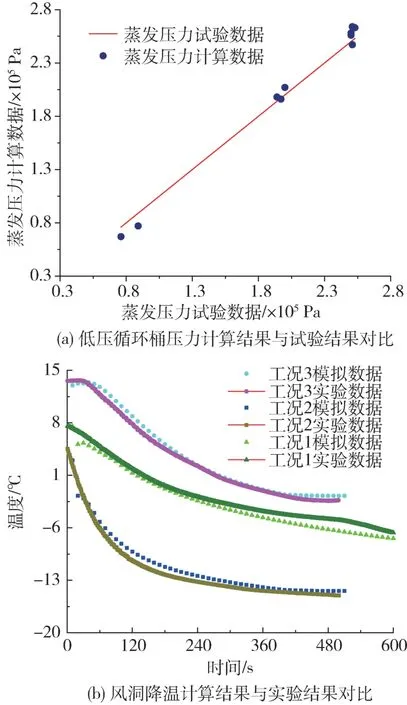
图2 计算模型验证Fig.2 Validation of calculation model

3 基于BP 神经网络模型的蒸发压力预测

BP (back propagation) 神经网络是1986 年由Rumelhart 和McClelland 为首的科学家提出的概念,是一种按照误差逆向传播算法训练的多层前馈神经网络,是目前广泛应用的神经网络模型。BP 神经网络算法以误差平方为目标函数、采用梯度下降法计算目标函数的误差最小值,其计算流程主要包括了两部分:正向结果计算和反向误差传递。

BP 神经网络的隐含层节点数对BP 神经网络预测精度有较大影响:当节点数太少时,网络不能很好的学习,需要增加训练次数,训练的精度也受影响;当节点数太多时,训练时间增加,网络容易过拟合。最佳隐含层节点数选择参考如式(17),并在范围内取训练最优值:

式中:l为隐含层节点数;m为输出层节点数;n为输入层节点数;a为0—10 之间的常数。

通过制冷系统蒸发压力热力学预测模型获得了数据样本,结合试验数据搭建BP 神经网络算法模型。数据样本来源包括50 组试验数据和50 组模型预测数据,以正交设计的25 组模型预测数据作为测试集。模型训练及预测均在LabVIEW 平台实现,可在软件中补充试验数据,对模型进行重新训练。

本研究选用均方误差(MSE)作为BP 神经网络模型训练的评价标准。在训练次数相同的条件下,进行不同隐藏层神经元个数对训练结果的影响分析,如图3a 所示。结果表明训练误差随着神经元个数变化呈现先减小后增大的趋势,存在过拟合情况和最优隐藏层神经元个数。因此,在预测模型中给定训练次数,通过模型预测误差最小化实现隐含层节点数的自动寻优。现有模型的自动寻优训练结果如图3b 所示。结果表明80%的预测值的绝对偏差小于0.1 ×105Pa,满足结冰风洞制冷系统蒸发压力控制需求。

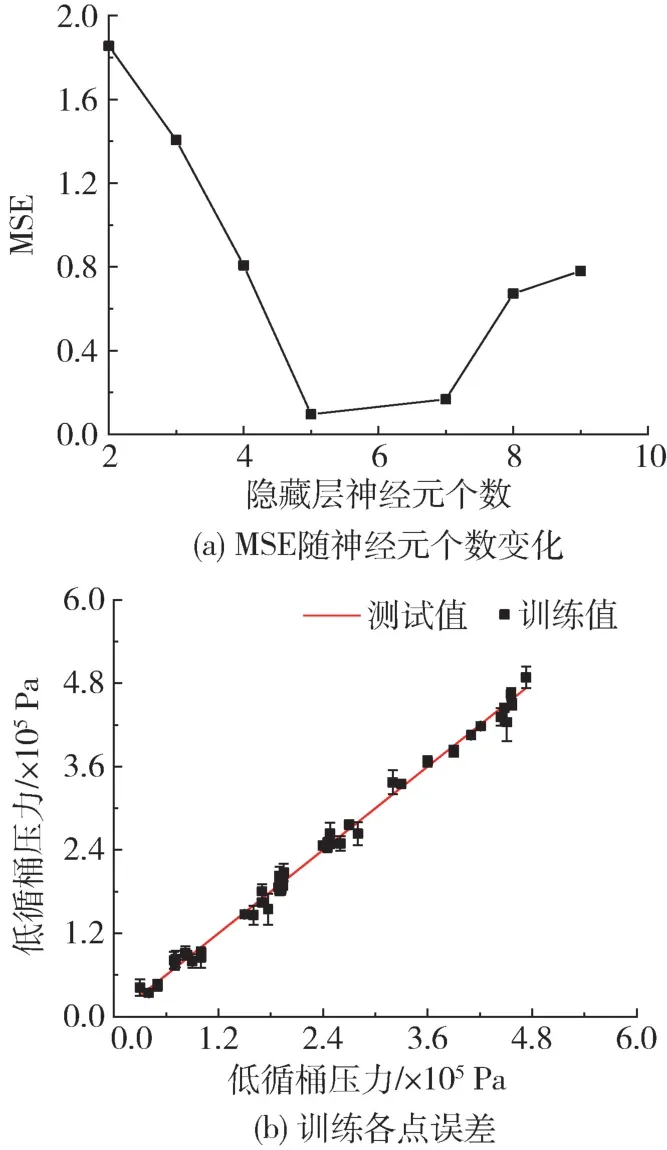
图3 BP 神经网络优化Fig.3 Optimization of BP neural network

4 风洞降温分析

风洞降温受试验高度和试验风速的影响,降温时间和降温能耗在不同条件下会产生差异,针对试验高度和试验风速对风洞的影响进行研究,提出降温控制方案。

4.1 试验高度对风洞降温的影响

在试验风速分别为37 m/s、93 m/s 和150 m/s,低压循环桶压力为2.45 ×105Pa,外界温度为7 ℃的初始条件下,研究了试验高度分别为0、2、3、5、7 km条件下的风洞降温情况,忽略试验中抽气减压的时间。仿真计算结果如图4 所示,可以看出随着高度的升高,风洞回路中的稳态温度呈现降低趋势。

图4 不同高度下的蒸发器出口温度降温曲线Fig.4 Evaporator outlet temperature at different altitude during the cooling-down process and wind speed

风机功率-高度-速度关系见图5,结果表明在相同的风速情况下,试验高度越高,风机功率越低,风洞系统的热负荷更小。以降温到-7 ℃为标准统计各试验高度下的降温时间,结果统计如图6 所示。图6表明降温时间与试验高度变化呈负相关,随着高度越高,洞体内部压力下降,系统热负荷下降,降温所需时间变短。高度变化会改变空气压力影响换热,高度升高也会减小风机功率,两者共同影响造成了降温时间变化程度越来越小。考虑风洞降温时的制冷系统能耗和风机能耗,各高度下降温至-7 ℃时的能耗结果统计如图7,结果表明高度越高,系统降温系统能耗随之减小。当试验风速较高时,导致风机能耗及系统热负荷显著上升,试验高度的影响更加明显。因此,对于高空环境试验,先进行风洞降压再降温,可以有效缩短降温时间、减小系统能耗。

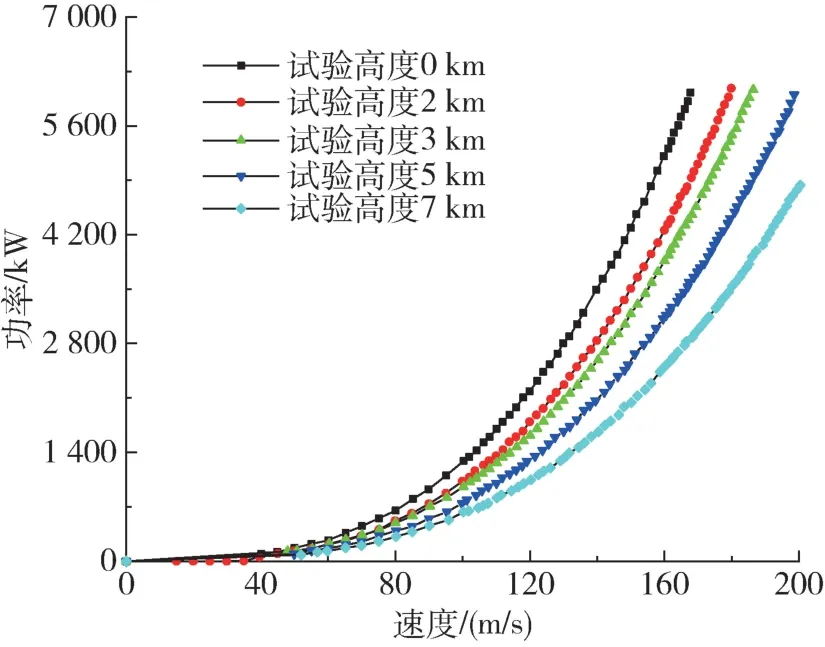
图5 主试验段风机在不同试验高度条件下的功率随风速的变化曲线Fig.5 Variations of fan power with wind speed under different tested altitude

图6 不同试验风速下的风洞降温时间随试验高度的变化Fig.6 Variations of cooling-down time with tested altitude at different wind speed

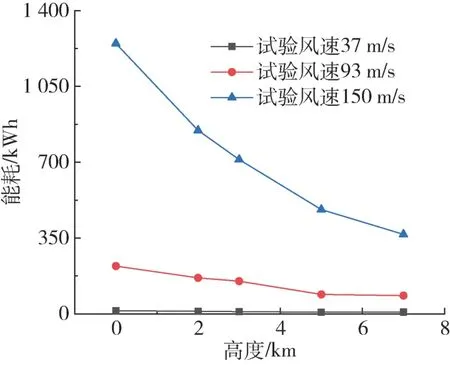
图7 不同试验风速下系统能耗随试验高度的变化Fig.7 Variations of system power with tested altitude at different wind speed

4.2 试验风速对风洞降温的影响

在蒸发器试验高度分别为0 km、3 km 和5 km,低压循环桶压力为2.45 ×105Pa,外界温度为7 ℃的初始条件下,研究了试验风速分别为37、56、75、100、130、150 m/s 条件下的风洞降温情况。仿真计算结果如图8 所示,可以看出随着风速的升高,风洞回路中的稳态温度呈现降温趋势,且降温时间变长。

图8 不同风速下蒸发器出口温度降温规律,试验高度Fig.8 Temporal variations of temperature at evaporator outlet under different wind speed and tested altitude

以降温到-7 ℃为标准统计各风速下的降温时间。从图9a 可以看出在低于100 m/s 的风速下,风洞降温时间变化不明显,降温时间随着风速的增大而降低,而在风速大于100 m/s 时降温时间变化相反。同时对各风速在对应时间下消耗的能量进行研究,计算结果如图所示,结果表明总消耗能量随着风速的增大而增大,当风速大于100 m/s 时,能耗快速上升,这是由于高风速下风机功率及其产生的热负荷快速上升所导致的。根据风机功率-高度-速度关系图,可以看出在相同高度下风机功率与风机速度呈现指数级上升趋势,极大地增加了风洞的热负荷。图片同时显示了试验高度对降温时间的影响情况,与前一节中的结论一致。同时统计各风速在对应时间下消耗的能量,结果如图9b 所示。结果表明功率变化规律与降温时间变化规律存在明显差别,总消耗能量随着风速的增大而增大,当风速大于100 m/s 时,能耗快速上升,这是由于高风速下风机功率及其产生的热负荷快速上升所导致的。由此可见,选取75 m/s 风速作为降温过程试验段风速条件时,可以实现最速降温,同时维持较低能耗。

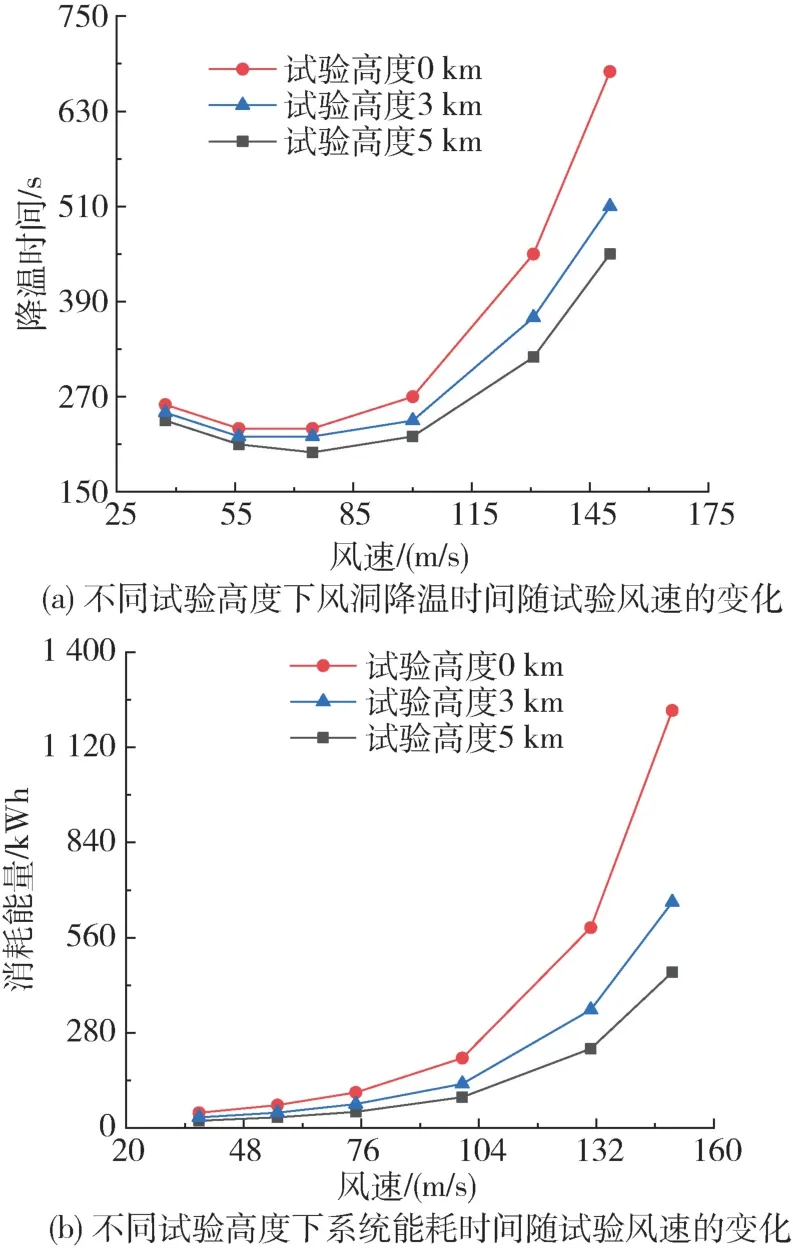
图9 试验风速优化Fig.9 Optimization of experimental wind speed

根据上述结果,继续进行变风速工况降温的研究,针对风速大于75 m/s 的工况(试验高度5 km),首先在75 m/s 降温到-7 ℃的情况下,再切换到指定风速进行降温。仿真计算结果如图10 所示。结果表明较原工况变风速工况在前段降温较快,待降到-7 ℃提高风速后,温度升高,降温稳定后变风速工况与原工况降温趋势逐渐一致。

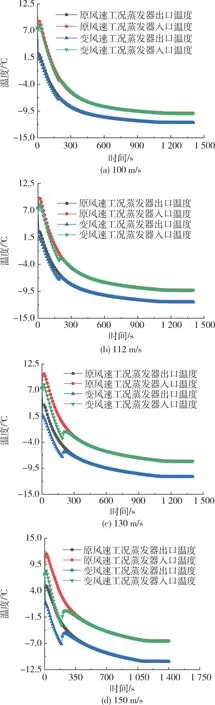
图10 不同试验风速下变风速降温过程Fig.10 Temperature variations during the cooling-down process with variable-wind speed design for different tested speed

同样对各工况降到-7 ℃(变风速工况调整风速后降温到-7 ℃)下消耗的能量(制冷系统功率和动力系统功率)进行统计研究,计算结果见图11。结果表明变风速对降温时间影响不大,但是大幅减少了能耗,且随着试验风速的升高,能耗降低幅度增大。上述结果为经济性最优降温策略提供了指导方案。

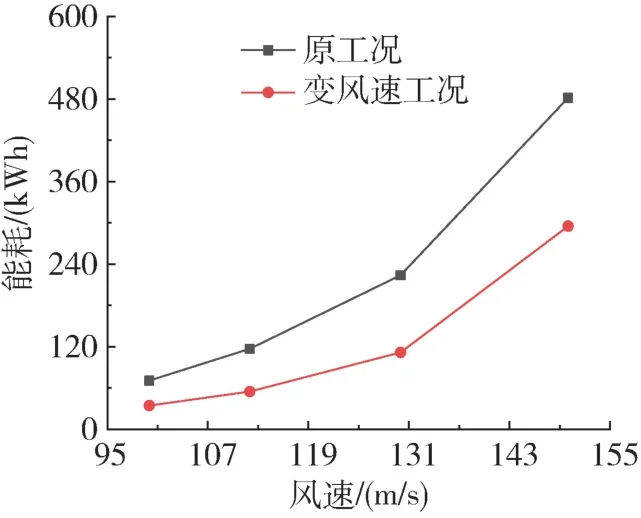
图11 变风速工况与原工况系统能耗随试验风速的变化Fig.11 Variations of system power consumption of variable-speed and fixed-speed cooling-down processes

5 结论

本研究针对大型结冰风洞复杂试验工况及制冷系统蒸发压力快速准确调节问题,建立了蒸发压力热力学预测模型,使用试验数据完成了模型验证。采用BP 神经网络模型,在LabVIEW 平台开发了制冷系统低压循环桶压力预测软件,实现了制冷系统调节过程低压循环桶压力快速预测。结果表明:

(1)试验风速75 m/s 时风洞系统降温速度最快。并且当试验风速分别为150 m/s、93 m/s 和37 m/s时,试验高度为7 km 的降温时间相比于高度为0 km 时的降温时间能缩短36%、20%和11%。

(2)对于高空环境试验,先进行风洞降压再降温,可以有效缩短降温时间、减小系统能耗。

(3)试验风速选择小于75 m/s 时风洞系统能耗最低。当试验高度为5 km 时,试验速度为75 m/s 的降温能耗相比于速度为150 m/s 时的降温能耗能降低83%。

(4)针对100 m/s、112 m/s、130 m/s 和150 m/s的风速进行变风速工况研究,发现降温能耗分别节省了27%、36%、50% 和45%。因此对于高风速试验,可以通过降温过程变风速控制方法降低系统能耗。