概率中的几类易错题剖析

湖北省襄阳市第五中学 闫小东

概率与统计是近几年高考考查的重点和热点问题,相关高考试题考查比较灵活,对同学们综合能力的考查要求比较高,本文以概率中几个常见易错题型为例进行剖析,希望能够帮助同学们解决学习概率过程中的一些疑惑。

易错题型一、古典概率模型理解不透而致误

例1一个盒中装有编号分别为1,2,3,4的四个形状大小完全相同的小球。

(1)从盒中任取两球,列出所有的基本事件,并求取出的球的编号之和大于6的概率;

(2)从盒中任取一球,记下该球的编号a,将球放回,再从盒中任取一球,记下该球的编号b,列出所有的基本事件,并求1的概率。

正解：(1)记“从盒中任取两球,取出球的编号之和大于6”为事件A,样本点（1,2）表示“从盒中取出1、2号球”,且(1,2)和(2,1)表示相同的样本点(其他情况类推),则样本空间为Ω=｛ (1,2),(1,3),(1,4),(2,3),(2,4),(3,4)｝,则A=｛ (3,4)｝,根据古典概型可知P(A)=,故从盒中任取两球,取出球的编号之和大于6的概率为

易错分析：有些同学可能误认为两球编号之和的基本事件总数有2,3,4,5,6,7,8,共7个,但是这7个结果并不是等可能发生的,不符合古典概型的定义,不能用古典概型解题。正确的结果应该是16个基本事件,这主要是同学们对古典概率模型的理解不透彻而出错。

易错题型二、条件概率模型理解不清而致误

例2甲、乙是北京2022 冬奥会单板滑雪坡面障碍技巧项目的参赛选手,二人在练习赛中均需要挑战3 次某高难度动作,每次挑战的结果只有成功和失败两种。

(1)甲在每次挑战中,成功的概率都为0.5。设X为甲在3 次挑战中成功的次数,求X的分布列和数学期望。

(2)乙在第一次挑战时,成功的概率为0.5,受心理因素影响,从第二次开始,每次成功的概率会发生改变,其规律为:若前一次成功,则该次成功的概率比前一次成功的概率增加0.1;若前一次失败,则该次成功的概率比前一次成功的概率减少0.1。

①求乙在前两次挑战中,恰好成功一次的概率;

②求乙在第二次成功的条件下,第三次成功的概率。

(2)设事件Ai为“乙在第i次挑战中成功”,其中i=1,2,3。

所以乙在前两次挑战中,恰好成功一次的概率为0.4。

所以乙在第二次成功的条件下,第三次成功的概率为0.62。

易错分析：有些同学容易混淆P(A2A3)和,在本题中,P(A2A3)表示第二次且第三次挑战成功发生的概率,P(A3)表示第二次挑战成功的条件下,第三次挑战成功发生的概率,可运用条件概率的计算公式计算),对条件概率的公式和条件概率模型的理解不清晰是致误的根源。

易错题型三、超几何分布与二项分布把握不准而致误

例3新冠肺炎疫情期间,各地均响应“停课不停学,停课不停教”的号召开展网课学习。为检验网课学习效果,某机构对2 000名学生进行了网上调查,发现有些学生上网课时有家长在旁督促,而有些没有,网课结束后进行考试,根据考试结果将这2 000 名学生分成“成绩上升”和“成绩没有上升”两类,对应的人数如表2所示:

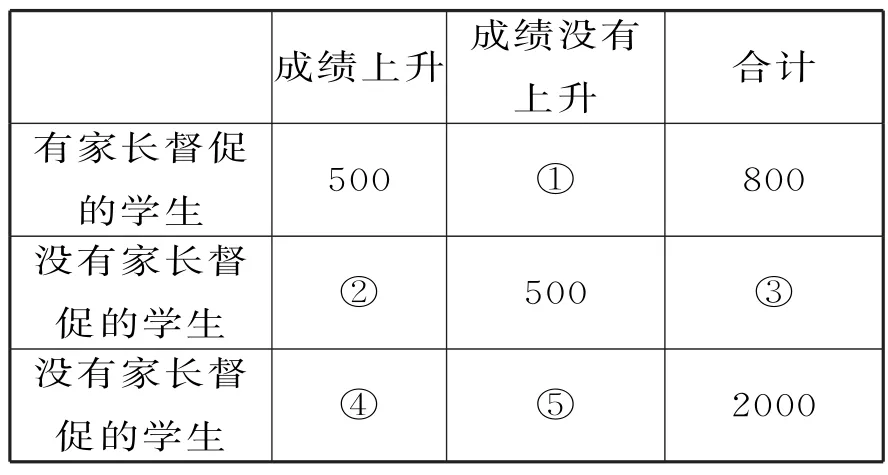
表2

(1)完成以上列联表,并通过计算(结果精确到0.001)说明是否有90%的把握认为家长督促学生上网课与学生的成绩上升有关联;

(2)从有家长督促的800名学生中按成绩是否上升,采用分层抽样的方法抽出8人,再从8人中随机抽取3人做进一步调查,记抽到3名成绩上升的学生得1分,抽到1名成绩没有上升的学生得-1分,设抽到3名学生的总得分用X表示,求X的分布列和数学期望;

(3)从这批网上调查的学生中抽取出3人,求恰有2人成绩上升的概率。

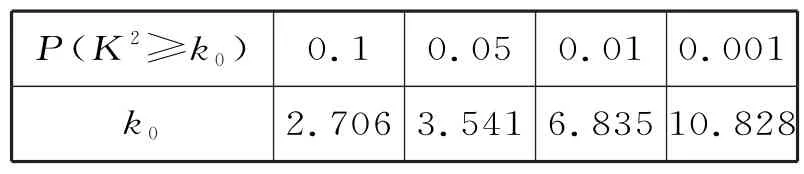
表3

正解：(1)①300;②700;③1 200;④1 200;⑤800。因为K2≈3.472＞2.706,所以有90%的把握认为家长督促学生上网课与学生的成绩上升有关联。

(2)从有家长督促的800 名学生中按成绩是否上升,采用分层抽样的方法抽出8人,其中成绩上升的有5人,成绩没有上升的有3人,再从8人中随机抽取3人,则随机变量X的所有可能取值为-3,-1,1,3。

所以X的分布列如表4:

表4

(3)从2 000名学生中抽取3人,成绩上升的人数近似服从二项分布记ξ表示抽到成绩上升的人数,ξ～B(3,

易错分析：有些同学容易对第(2)(3)问感到困惑。第(2)问从8人中抽出3人,属于总体容量比较小的情形,服从超几何分布。第(3)问从网上调查的2 000名学生中抽取3人,属于总体容量比较大的情形,近似看作n次独立重复试验,服从的是二项分布。对超几何分布和二项分布模型理解不到位是致误的根源。

总之,同学们要牢记与概率相关的概念公式,理解各类概率模型的基本内涵,精准把握各类概率模型的适用情境,这样才能轻松驾驭和解决概率问题。