概率统计试题精选

广东信宜教育局教研室 王位高

1.某财经杂志发起一项调查,旨在预测中国经济前景,随机访问了100位业内人士,根据被访问者的问卷得分(满分10 分)将经济前景预期划分为三个等级(悲观、尚可、乐观)。分级标准及这100 位被访问者的得分频数分布情况如表1所示:

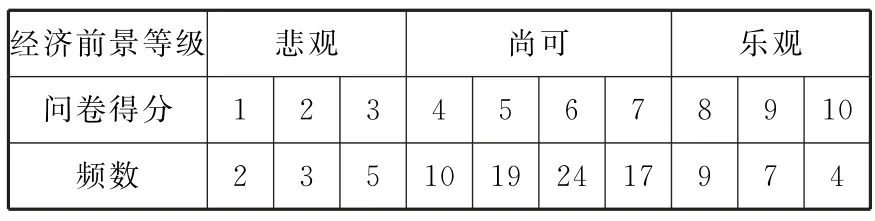
表1

假设被访问的每个人独立完成问卷(互不影响),根据经验,这100位人士的意见即可代表业内人士的意见,且他们预测各等级的频率可估计未来经济各等级发生的可能性。

(1)该杂志记者又随机访问了两名业内人士,试估计至少有一人预测中国经济前景为“乐观”的概率。

(2)某人有一笔资金,现有两个备选的投资意向:物联网项目或人工智能项目,两种投资项目的年回报率都与中国经济前景等级有关,根据经验,大致关系如表2 所示(正数表示赢利,负数表示亏损):

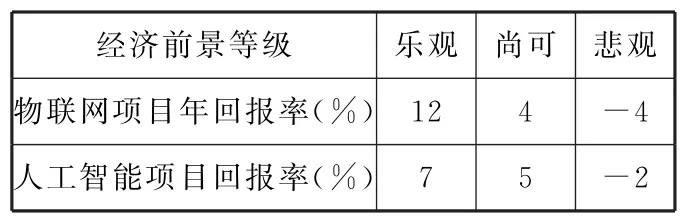
表2

根据以上信息,请分别计算这两种投资项目的年回报率的期望与方差,并用统计学知识给出投资建议。

2.2021年7月18日第30届全国中学生生物学竞赛在浙江省萧山中学隆重举行。为做好本次考试的评价工作,将本次成绩转化为百分制,现从中随机抽取了50名学生的成绩,经统计,这批学生的成绩全部介于40 至100之间,将数据按照[40,50),[50,60),[60,70),[70,80),[80,90),[90,100]分成6组,制成了如图1 所示的频率分布直方图。

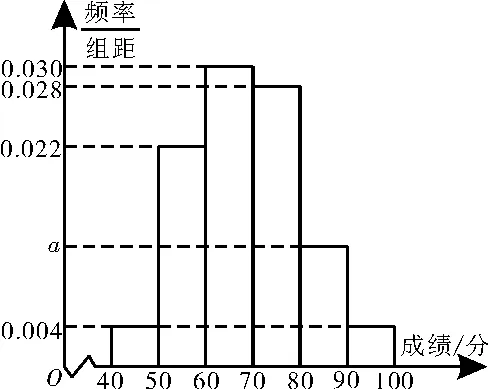
图1

(1)求频率分布直方图中m的值,并估计这50 名学生成绩的中位数。

(2)在这50名学生中用分层抽样的方法从成绩在[70,80),[80,90),[90,100]内的三组中抽取了11人,再从这11人中随机抽取3人,记ξ为3 人中成绩在[80,90)内的人数,求ξ的分布列和数学期望。

(3)转化为百分制后,规定成绩在[90,100]内的为A等级,成绩在[70,90)内的为B等级,其他为C等级。以样本估计总体,用频率代替概率,从所有参加生物学竞赛的同学中随机抽取100人,其中获得B等级的人数设为η,记B等级的人数为k的概率为P(η=k),写出P(η=k)的表达式,并求出当k为何值时,P(η=k)最大?

3.根据中国海洋生态环境状况公报,从2017年到2021年全国直排海污染物中各年份的氨氮总量y(单位:千吨)与年份的散点图,如图2所示。

记年份代码为x(x=1,2,3,4,5),,对数据处理后得到表3。

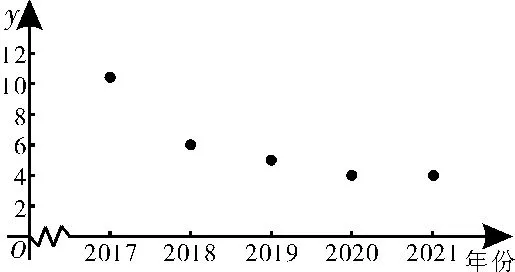
图2

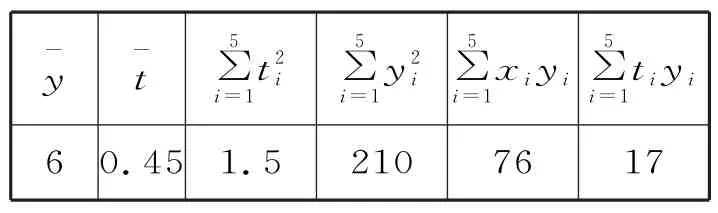
表3

(1)根据散点图判断,模型①y=bx+a与模型哪一个适宜作为y关于x的回归方程? (给出判断即可,不必说明理由)

(2)根据(1)的判断结果,建立y关于x的回归方程,并预测2022年全国直排海污染物中的氨氮总量(计算结果精确到0.01)。

4.中国男子篮球职业联赛(CBA)始于1995年,至今已有28 个赛季,根据传统,在每个赛季总决赛之后,要举办一场南北对抗的全明星比赛,其中三分王的投球环节最为吸引眼球,三分王投球的比赛规则如下:一共有五个不同角度的三分点位,每个三分点位有5个球(前四个是普通球,最后一个球是花球),前四个球每投中一个得1 分,投不中的得0分,最后一个花球投中得2分,投不中得0分。全明星参赛球员甲在第一个角度的三分点开始投球,已知球员甲投球的命中率为,且每次投篮是否命中相互独立。

(1)记球员甲投完1 个普通球的得分为X,求X的方差D(X);

(2)若球员甲投完第一个三分点位的5个球后共得到了2 分,求他是投中了花球而得到了2分的概率;

(3)在比赛结束后与球迷的互动环节中,将球员甲在前两个三分点位使用过的10 个篮球对应的小模型放入箱中,由幸运球迷从箱中随机摸出5个小模型,并规定,摸出一个花球小模型计2 分,摸出一个普通球小模型计1分,求该幸运球迷摸出5个小模型后的总计分Y的数学期望。

5.根据社会人口学研究发现,一个家庭有X个孩子的概率模型为表4:

表4

其中α＞0,0＜p＜1。每个孩子的性别是男孩还是女孩的概率均为,且相互独立,事件Ai表示一个家庭有i个孩子(i=0,1,2,3),事件B表示一个家庭的男孩比女孩多(例如:一个家庭恰有一个男孩,则该家庭男孩多)

(1)若p=,求α,并根据全概率公式,求P(B)。

(2)为了调控未来人口结构,其中参数p受到各种因素的影响(例如:生育保险的增加,教育、医疗福利的增加等)。

①若希望P(X=2)增大,则该如何调控p的值?

②是否存在p的值使得,请说明理由。

6.2022年9月28日晚,中国女排在世锦赛小组赛第三轮比赛中,又一次以3∶0的比分酣畅淋漓地战胜了老对手日本女排,冲上了热搜榜第八位,令国人振奋! 同学们,你们知道排球比赛的规则和积分制吗? 其规则是:每场比赛采用“5局3胜制”(有一支球队先胜3局即可获胜,比赛结束)。比赛排名采用积分制,积分规则如下:比赛中,以3∶0或3∶1取胜的球队积3分,负队积0分;以3∶2取胜的球队积2分,负队积1分。已知甲、乙两队比赛,甲队每局获胜的概率为

(1)如果甲、乙两队比赛1 场,求甲队的积分X的概率分布列和数学期望;

(2)如果甲、乙两队约定比赛2 场,求两队积分相等的概率。

7.调查表明:甲种农作物的长势与海拔高度、土壤酸碱度、空气湿度的指标有极强的相关性,现将这三项的指标分别记为x,y,z,并对它们进行量化:0表示不合格,1表示临界合格,2 表示合格,再用综合指标ω=x+y+z的值评定这种农作物的长势等级,若ω≥4,则长势为一级;若2≤ω≤3,则长势为二级;若0≤ω≤1,则长势为三级。为了了解目前这种农作物的长势情况,研究人员随机抽取10块种植地,得到表5中的结果:

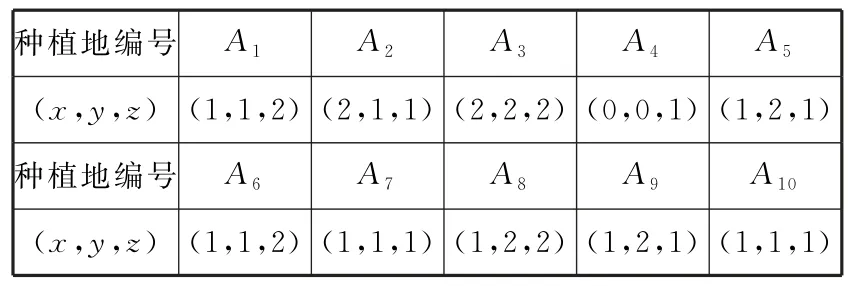
表5

(1)在这10块该农作物的种植地中任取两块地,求抽取的两块地的空气湿度的指标z相同的概率;

(2)从长势等级是一级的种植地中任取一块地,其综合指标为A,从长势等级不是一级的种植地中任取一块地,其综合指标为B,记随机变量X=A-B,求X的分布列及其数学期望。

8.已知5 只动物中有1 只患有某种疾病,需要通过化验血液来确定患病的动物。血液化验结果呈阳性的即为患病动物,呈阴性即没患病。现有两种化验方案,方案甲:逐个化验,直到能确定患病动物为止。方案乙:先任取3 只,将它们的血液混在一起化验。若结果呈阳性,则表明患病动物为这3 只中的1只,然后再逐个化验,直到能确定患病动物为止;若结果呈阴性,则在另外2只中任取1只化验。

(1)求依方案甲所需化验次数不少于依方案乙所需化验次数的概率;

(2)ξ表示依方案乙所需化验次数,求ξ的期望。

9.某市为提升中学生的数学素养,激发学生学习数学的兴趣,举办了一次“数学文化知识大赛”,分预赛和复赛两个环节,已知共有8 000名学生参加了预赛,现从参加预赛的全体学生中随机地抽取100人的预赛成绩作为样本,得到如图3 所示的频率分布直方图。

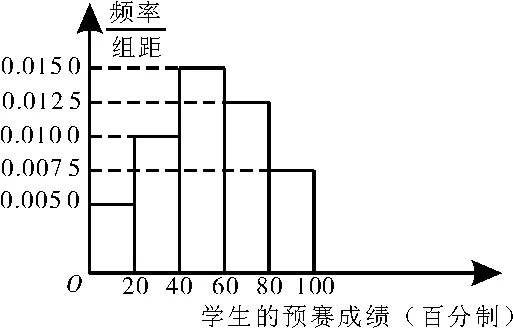
图3

(1)规定预赛成绩不低于80分为优良,若从上述样本中预赛成绩不低于60分的学生中随机地抽取2 人,求恰有1 人预赛成绩优良的概率。

(2)由频率分布直方图可认为该市全体参加预赛学生的预赛成绩Z服从正态分布N（μ,σ2）,其中μ可近似为样本中的100 名学生预赛成绩的平均值(同一组数据用该组区间的中点值作代表),且σ2=362。利用该正态分布,估计全市参加预赛的全体学生中预赛成绩不低于91分的人数。

(3)预赛成绩不低于91分的学生将参加复赛,复赛规则如下:①每人的复赛初始分均为100分;②参赛学生可在开始答题前自行决定答题数量n,每一题都需要“花”掉(即减去)一定分数来获取答题资格,规定答第k题时“花”掉的分数为0.1k(k=1,2,…,n);③每答对一道题加1.5 分,答错既不加分也不减分;④答完n道题后参赛学生的最终分数即为复赛成绩。已知学生甲答对每道题的概率均为0.7,且每道题答对与否都相互独立。若学生甲期望获得最佳的复赛成绩,则他的答题数量n应为多少?

10.足球运动被誉为“世界第一运动”。为了推广足球运动,某学校成立了足球社团。由于报名人数较多,需对报名者进行“点球测试”来决定是否录取,规则如图4所示:

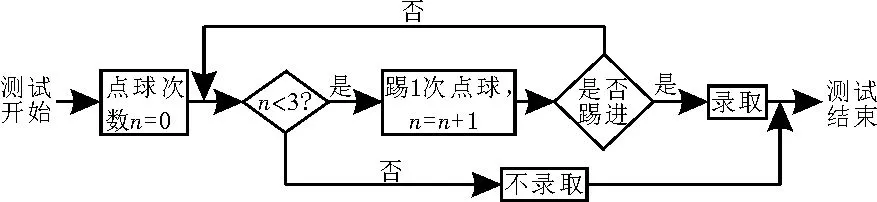
图4

(1)表6是某同学6次的训练数据,以这150个点球中的进球频率代表其单次点球踢进的概率。为加入足球社团,该同学进行了“点球测试”,每次点球是否踢进相互独立,将他在测试中所踢的点球次数记为ξ,求E(ξ)。

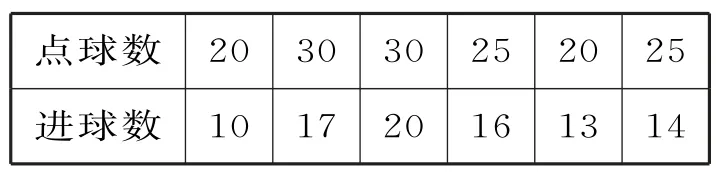
表6

(2)社团中的甲、乙、丙三名成员将进行传球训练,从甲开始随机地将球传给其他两人中的任意一人,接球者再随机地将球传给其他两人中的任意一人,如此不停地传下去,且假定每次传球都能被接到。记开始传球的人为第1次触球者,接到第n次传球的人即为第n+1次触球者(n∈N*),第n次触球者是甲的概率记为Pn。

①求P1,P2,P3(直接写出结果即可);

参考答案：

1.(1)由题意可得,在100 名被采访者中,预测中国经济前景为“乐观”的人数为9+7+4=20,故若随机访问两名业内人士,至少有一人预测中国经济前景为“乐观”的概率

(2)由题意可得,在100 名被采访者中,预测中国经济前景为“乐观”的概率为0.2;预测中国经济前景为“尚可”的概率为;预测中国经济前景为“悲观”的概率为

故建议投资人工智能项目。

2.(1)由频率分布直方图的性质可得,(0.004+m+0.022+0.03+0.028+0.004)×10=1,解得m=0.012,设中位数为n,则0.004×10+0.022×10+(n-60)×0.03=0.5,解得n=68。

故ξ的分布列为表7:

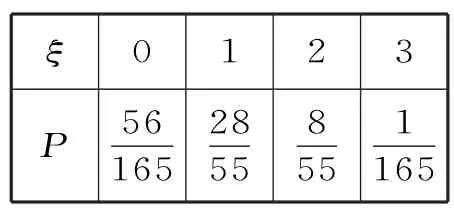
表7

3.(1)根据散点图的趋势,可知模型②适宜作为y关于x的回归方程。

故预计2022 年全国直排海污染物中的氨氮总量为3.97吨。

记g(p)=2p3-3p2-1,则g′(p)=6p2-6p=6p(p-1)＜0,故g(x)在(0,1)上单调递减。

因为g(0)=-1,所以g(p)＜0,f(p)在(0,1)上单调递减。

因此增加p的取值,会减小,α增大,即P(X=2)增大。

所以X的分布列为表8:

表8

(2)记“甲、乙两队比赛两场后,两队积分相等”为事件A,设第i场甲、乙两队积分分别为Xi、Yi,则Xi=3-Yi,i=1,2。

因为两队积分相等,所以X1+X2=Y1+Y2,即X1+X2=(3-X1)+(3-X2),则X1+X2=3。

7.(1)由题表可知,空气湿度指标为1的有A2,A4,A5,A7,A9,A10;空气湿度指标为2的有A1,A3,A6,A8。

抽取的两块地的空气湿度的指标z相同包含的基本事件个数

所以抽取的两块地的空气湿度的指标z相同的概率

(2)由题意得,这10 块种植地的综合指标如表9所示:

表9

其中长势等级是一级(ω≥4)的有A1,A2,A3,A5,A6,A8,A9,共7 个,长势等级不是一级(ω＜4)的有A4,A7,A10,共3个,随机变量X=A-B的所有可能取值为1,2,3,4,5,w=4 的有A1,A2,A5,A6,A9,共5 个,w=3的有A7,A10,共2个,这时有X=4-3=1。

所以X的分布列为表10:

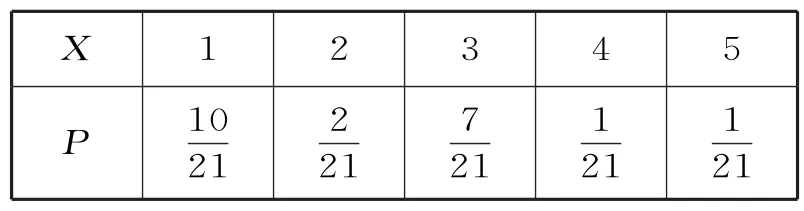
表10

8.(1)设A1、A2分别表示依方案甲需化验1次、2次,B1、B2表示依方案乙需化验2次、3次,A表示依方案甲所需化验次数不少于依方案乙所需化验次数。

9.(1)易知样本中成绩不低于60分的学生共有(0.012 5+0.007 5)×20×100=40(人),其中成绩优良的人数为0.007 5×20×100=15(人)。

记“从样本中成绩不低于60分的学生中随机地抽取2人,恰有1人成绩优良”为事件C,则

(2)由题意可知,样本中的100名学生预赛成绩的平均值为x=10×0.1+30×0.2+50×0.3+70×0.25+90×0.15=53,则μ=53,由σ2=362得σ≈19。

所以P(Z≥91)≈P(Z≥μ+2σ)=[1-P(μ-2σ＜Z＜μ+2σ)]≈0.022 75,由此可估计全市参加预赛的全体学生中预赛成绩不低于91分的人数为8 000×0.022 75=182(人),即全市参赛学生中成绩不低于91分的人数为182。

(3)以随机变量ξ表示甲答对的题数,则ξ～B(n,0.7),且E(ξ)=0.7n。

记甲答完n道题所加的分数为随机变量X,则X=1.5ξ,所以E(X)=1.5E(ξ)=1.05n。

依题意,为了获取答n道题的资格,甲需要“花”掉的分数为0.1×(1+2+3+…+n)=0.05(n2+n)。

设甲答完n道题的最终分数为M(n),则M(n)=100-0.05(n2+n)+1.05n=-0.05(n-10)2+105。

由于n∈N*,所以当n=10时,M(n)取最大值105,即复赛成绩的最大值为105。

所以若学生甲期望获得最佳的复赛成绩,则他的答题数量n应为10。

由题意知,ξ的所有可能取值为1,2,3,则P(ξ=1)=0.6;P(ξ=2)=0.6×0.4=0.24;P(ξ=3)=0.42=0.16。

所以期望E(ξ)=1×0.6+2×0.24+3×0.16=1.56。