关于回归方程的解题策略及技巧
2023-03-19江苏省锡东高级中学顾珊岚
江苏省锡东高级中学 顾珊岚
回归方程是利用数理统计中的回归分析,来确定两种或两种以上变数间相互依赖的定量关系的一种统计分析方法,运用十分广泛。近几年高考所涉及的题目愈发凸显其应用性,以及问题设计的新颖性、创造性。同学们只有充分理解回归方程,冷静分析问题的本质,才能以不变应万变。下面我们对近几年回归方程考题的变化及趋势作归纳与梳理。
一、线性回归方程
例1某科技公司研发了一项新产品A,经过市场调研,对公司1月份至6月份销售量及销售单价进行统计,销售单价x(千元)和销售量y(千件)之间的一组数据如表1所示:
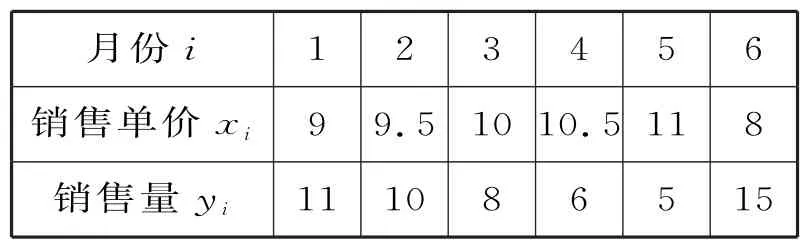
表1
(1)试根据1至5月份的数据,建立y关于x的回归直线方程;
(2)若由回归直线方程得到的估计数据与剩下的检验数据的误差不超过0.65千件,则认为所得到的回归直线方程是理想的,试问(1)中所得到的回归直线方程是否理想?
例2人工智能教育是将人工智能与传统教育相结合,借助人工智能和大数据技术打造的智能化教育生态。为了解我国人工智能教育发展状况,通过中国互联网数据平台得到我国2017年至2022年人工智能教育市场规模统计图,如图1所示,若用x表示年份代码(2017年用1表示,2018年用2表示,依此类推),用y表示市场规模(单位:亿元),试回答:
(1)根据条形统计图中的数据,计算变量y与x的相关系数r,并用r判断两个变量y与x相关程度的强弱(精确到0.01)(若,则相关程度很高);
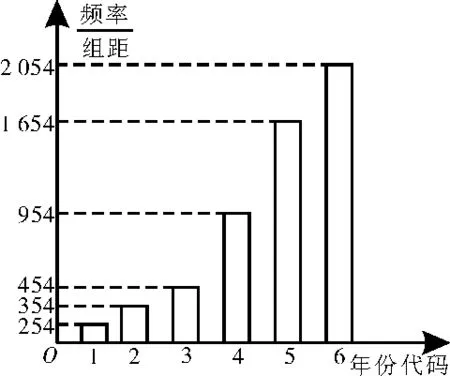
图1
(2)若y与x的相关关系拟用线性回归模型表示,试求y关于x的线性回归方程,并据此预测2024 年中国人工智能教育市场规模(精确到1亿元)。
点评:此类考题难度偏小,线性回归方程的求解直接利用题中公式及数据计算即可,再利用线性回归方程进行数据估计。
二、非线性回归方程
例3某印刷企业为了研究某种图书每册的成本费y(单位:元)与印刷数量x(单位:千册)的关系,收集了一些数据并进行了初步整理,得到了如图2所示的散点图及一些统计量的值(表2)。

图2

表2
(1)根据散点图判断:y=a+bx与y=哪一个模型更适合作为该图书每册的成本费y与印刷数量x的回归方程? (只要求给出判断,不必说明理由)
(2)根据(1)的判断结果及表中数据建立y关于x的回归方程(结果精确到0.1)。
(3)若该图书每册的定价为9元,求至少应该印刷多少册,才能使销售利润不低于80 000元(假设能够全部售出)。
附:对于一组数据(ω1,v1)(ω2,v2),…(ωn,vn),其回归直线的斜率和截距的最小二乘估计公式分别为
解析:(1)由散点图判断更适合作为该图书每册的成本费y与印刷数量x的回归方程。
例4学生的学习除了在课堂上认真听讲,还有一个重要环节就是课后的“自主学习”,包括预习,复习,归纳,整理等,现在人们普遍认为课后花的时间越多越好,某研究机构抽查了部分高中学生,对学生花在课后的学习时间(设为x分钟)和他们的数学平均成绩(设为y)进行了统计,得到表3中的数据,请根据表格回答问题:

表3
(1)请根据所给数据绘制散点图,并且从以下三个函数:①y=bx+a;②y=m·xk(m>0,k>0);③y=cx2+dx+e中选择一个作为学习时间x和平均成绩y的回归类型,判断哪个类型更加符合(不必说明理由)。
(2)根据(1)中选择的回归类型,求出y与x的回归方程。
解析:(1)根据所给数据画得散点图,如图3所示。
根据散点图判断y=m·xk(m>0,k>0)更符合学习时间x和平均成绩y的回归方程类型。
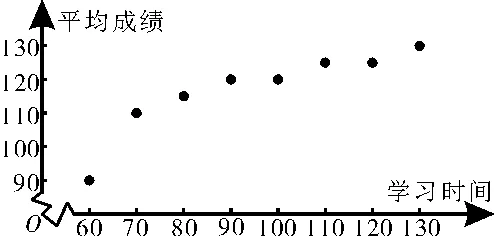
图3
故回归方程为y=25.79x0.33。
点评:对于给出多个模拟函数类型的非线性回归,我们可以根据数据的散点图,将它与学过的各种函数的图像进行比较,选择一种跟散点拟合得最好的函数,然后采取适当的变量代换,将非线性回归方程转化为线性回归方程。
回归方程一直是高考数学的热点,在高考备考时,要重视阅读理解,注重体验回归方程的思维分析过程,根据散点图判断回归模型是线性还是非线性。如果是线性则直接套公式;如果是非线性,则要通过数学变换将非线性转化为线性关系,利用最小二乘法求出线性回归方程系数,进而求出线性回归方程,最后通过数学变换还原求出非线性回归方程。
