独立性检验热点题型例析

江苏省天一中学 孙承辉

独立性检验是统计中的一个重要知识点,主要是根据2×2 列联表计算K2的值,从而判断两个事件之间是相互独立还是存在某种关联性。考题的呈现形式多种多样,一般与概率统计中的其他知识交汇,体现一定的综合性。本文精选一些典型例题,希望对同学们的复习能有所帮助。

题型一、独立性检验与频率分布直方图交汇

这类题目以频率分布直方图为背景,为检验事件的独立性提供数据。解题的关键是读懂频率分布直方图,明确各小长方形的面积表示相应各组的频率,从而求出相应区间内的样本频数,并完善2×2 列联表和计算K2的值。

例 1致敬百年,读书筑梦,某学校组织全校学生参加“学党史颂党恩,党史网络知识竞赛”活动,并从中抽取100 名学生的竞赛成绩作为样本进行统计,得到如图1所示的频率分布直方图。规定:成绩在[80,100]内为优秀,成绩低于60分为不及格。

(1)求a的值,并用样本估算总体,能否认为该校参加本活动的学生成绩符合“不及格的人数低于20%”的要求?

(2)根据以上数据完成表1所示的2×2列联表,并判断是否有99%的把握认为此次竞赛成绩与性别有关。

表2

解析：(1)(0.004+a+0.011+0.036+0.023+0.014+a)×10=1,解得a=0.006,成绩不及格的频率为(0.004+0.006+0.011)×10=0.21,所以“成绩不及格”的概率估计值为21%。

因为21%＞20%,所以不能认为该校参加本活动的学生成绩符合“不及格的人数低于20%”的要求。

(2)由(1)可得,成绩在［80,100］内的人数为(0.014+0.006)×10×100=20,即样本中成绩优秀的有20人,由此完成2×2 列联表,如表3所示:

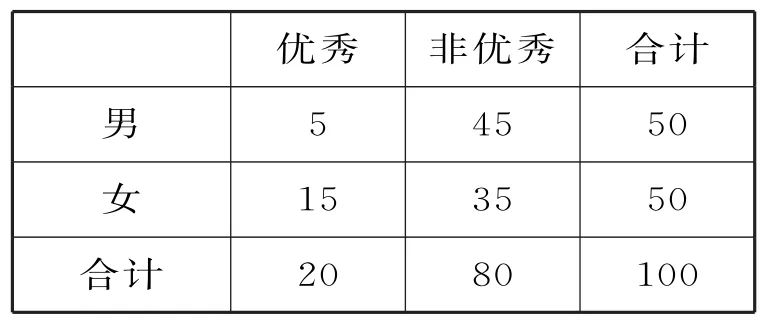
表3

假设H0:此次竞赛成绩与性别无关,则

所以没有99%的把握认为此次竞赛成绩与性别有关。

点评:本题第(1)问先利用概率分布直方图的性质求出a=0.006,进而求得60 分以下的概率估计值,即可判断;第(2)问先根据第(1)问中的结论,求得优秀的人数,再填写列联表,进而求出K2的值,查表后可以判断得出没有99%的把握。

题型二、独立性检验与相关系数交汇

样本相关系数r可以反映成对样本数据的变化特征,当|r|越接近1 时,成对样本数据的线性相关程度越强;当|r|越接近0 时,成对样本数据的线性相关程度越弱。解决与相关系数有关的独立性检验问题时,要理解r和K2的计算公式中各个数据的含义。

例2共享汽车,是指许多人合用一辆车,即开车人对车辆只有使用权,而没有所有权,有点类似于在租车行业里的短时间的租车。它手续简便,打个电话或通过网上就可以预约订车。某市为了了解不同年龄的人对共享汽车的使用体验,随机选取了100 名使用共享汽车的体验者,让他们根据体验效果进行评分。

(1)设消费者的年龄为x,对共享汽车的体验评分为y。若根据统计数据,用最小二乘法得到y关于x的线性回归方程为1.5x+15,且年龄x的方差为,评分y的方差为。求y与x的相关系数r,并据此判断对共享汽车使用体验的评分与年龄的相关性强弱(当|r|≥0.75时,认为相关性强,否则认为相关性弱)。

(2)现将100名消费者的年龄划分为“青年”和“中老年”,评分划分为“好评”和“差评”,整理得到表4的一些数据,请将表4 所示的2×2 列联表补充完整,并判断是否有99.9%的把握认为对共享汽车的评价与年龄有关。

临界值表(表5):

表5

因为0.9＞0.75,所以可判断对共享汽车使用体验的评分与年龄的相关性很强。

(2)根据题意可得完整的2×2 列联表,如表6所示:

表6

点评:第(1)问根据公式求出相关系数r,计算过程中注意整体代入,再与0.75比较即可得出结论;第(2)问直接根据已有数据即可完成已知列联表,再根据公式求出K2的值,然后对照临界值表即可得出结论。

题型三、独立性检验与概率交汇

统计与概率的相关知识密不可分,独立性检验问题经常与概率交汇在一起,重点考查古典概型、随机变量的概率分布、数学期望等知识。

例3某种疾病可分为A,B两种类型,为了解该疾病的类型与患者性别是否相关,在某地区随机抽取了若干名该疾病的患者进行调查,发现女性患者人数是男性患者的2倍,男性患A型疾病的人数占男性患者的,女性患A型疾病的人数占女性患者的

(1)若本次调查得出“在犯错误的概率不超过0.005的前提下认为‘所患疾病的类型’与‘性别’有关”的结论,试问:被调查的男性患者至少有多少人?

(2)某团队进行预防A型疾病的疫苗的研发试验,试验期间至多安排2 个周期接种疫苗,每人每个周期接种3次,每次接种费用为m(m＞0)元。该团队研发的疫苗每次接种后产生抗体的概率为p(0＜p＜1),如果一个周期内至少2 次出现抗体,则该周期结束后终止试验,否则进入第二个周期。若,试验人数为1 000 人,试估计该试验用于接种疫苗的总费用。

表7

解析：(1)设男性患者有x人,则女性患者有2x人,整理可得完整的2×2列联表,如表8所示:

表8

假设H0:患者所患疾病类型与性别之间无关联,根据列联表中的数据,经计算得到

要使在犯错误的概率不超过0.005的前提下认为“所患疾病类型”与“性别”有关,则,解得x＞11.818 5。

(2)设该试验每人的接种费用为ξ元,则ξ的所有可能取值为3m,6m。

点评:第(1)问根据数据设男性患者有x人,则女性患者有2x人,即可得到2×2列联表,计算出K2的值,从而得到不等式,求出x的取值范围是x＞11.818 5,同时注意到x必须是6 的倍数,所以x的最小整数值为12。第(2)问设该试验每人的接种费用为ξ元,则ξ的可能取值为3m,6m,求出所对应的概率,即可求出数学期望,再由和试验人数为1 000人,求出总费用的期望值。