基于FRANC3D的轮轨疲劳裂纹扩展研究
2023-03-19张学飞曹兆风王志坚
张学飞,曹兆风,王志坚
(常州大学城市轨道交通学院,江苏 常州 213164)
1 引言
随着列车运行速度的提高及轴重的变化,使得轮轨间的接触疲劳越来越严重,出现了踏面裂纹、硌伤等轮轨损伤问题[1−2],对于列车运行的平稳性、舒适性和安全性产生严重影响。所以,对轮轨裂纹的研究显得尤为重要。在裂纹分析中,对于一些复杂构形的裂纹结构,部分学者采用了数值方法。文献[3−4]对利用数值法对内部裂纹的应力和应变分布进行了研究。文献[5]利用有限元的方法建立了不同长度、不同角度的车轮内部裂纹,进而得到了不同工况下裂纹周边以及轮轨接触区的Mises 应力分布规律。文献[6]在使用ANSYS研究轮轨疲劳裂纹的萌生时发现,随着轴重的增加,轮轨最大Mises应力、最大接触法向应力和接触疲劳裂纹萌生速率也会随之增大。
由于裂纹尖端处的应力具有奇异性,在研究和分析裂纹时,网格质量对求解精度的影响是不容忽视的。尽管许多有限元软件可以对裂纹结构进行精确的应力分析,但是在网格划分方面,尤其是对于一些复杂的裂纹结构,在进行网格划分的时候往往需要对模型进行多次切分,甚至最终并不能得到理想的网格模型。而FRANC3D 软件的自适应网格划分功能很好地解决了这一问题,并且还能计算裂纹的自动扩展和结构的疲劳寿命,在许多行业已经有了广泛的应用。文献[7]利用FRANC3D软件对叶片在疲劳裂纹作用下的多次断裂进行了分析。文献[8]对齿轮疲劳裂纹扩展进行了数值模拟分析,研究表明,裂纹扩展过程中以Ⅰ型裂纹为主,应力强度因子随裂纹扩展长度的增加而增大。文献[9]通过计算一个应用实例,验证了实验值与FRANC3D 预测值的准确性。文献[10]对轮盘三维裂纹进行了分析,并利用该软件绘制出轮盘裂纹扩展的疲劳寿命曲线。
虽然FRANC3D在其他行业发挥了很大的作用,但其在轮轨裂纹的问题上应用甚少。当车轮出现裂纹时,裂纹的起始位置和角度不尽相同,因此需要研究各种参数对车轮裂纹应力强度因子的影响及其规律。将该方法应用到轮轨裂纹问题上,依据边界元的思想,结合断裂力学的知识,使用FRANC3D 软件在车轮不同位置插入不同长度、不同角度及不同深度的裂纹来研究三维裂纹的应力强度因子。
2 疲劳裂纹扩展的理论依据
2.1 裂纹尖端奇异性
在弹性力学中,裂纹尖端附近应力场可由含1/r项的式子表示:
式中:r、θ—求σ值所在点的圆柱形极坐标;(fθ)—无量纲参数。
当r→0,θ→0时,裂纹尖端附近点的应力将趋于无穷大,称为应力的奇异性[10]。然而这种情况实际并不存在,当应力达到材料的屈服极限时,裂纹尖端便会发生塑性变形从而使应力得到松弛,同时形成一个微小的塑性区域。但是,虽然此时裂纹尖端的应力趋于无穷大,其应力强度因子却是有限值。
2.2 应力强度因子
断裂力学中反映裂纹尖端弹性应力场强弱的物理量称为裂纹尖端应力场强度因子,简称应力强度因子(SIF),一般来说,应力强度因子可写成如下形式[11]:
式中:σ—名义应力,即裂纹位置上按无裂纹计算的应力;
a—裂纹几何尺寸;
α—形状系数(与裂纹几何尺寸、位置等有关)。
根据线弹性断裂力学理论[12],裂纹是否会扩展主要取决于裂纹尖端的应力强度因子KI,若KI小于材料的断裂韧性KIC,则构件能够继续安全使用,否则就必须对裂纹进行消除。KIC是平面应变状态下I型裂纹尖端应力强度因子KI的临界值,称为材料的平面应变断裂韧度。KIC是材料本身的属性,其数值取决于物体和裂纹的几何形状、加载状况、试验环境。
2.3 FRANC3D软件工作机理
FRANC3D软件能够很好地模拟三维裂纹扩展行为,是一款专门用于断裂分析的自由软件,主要针对应力强度因子、裂纹自动扩展和疲劳寿命的计算。
其功能和应用介绍见文献[11]。FRANC3D有很强的模拟裂纹的能力,可以生成多种类型的裂纹,如多裂纹、非平面裂纹和任意形状的裂纹,用户可以根据需要在模型任意位置中加入所需的裂纹。并且在裂纹扩展后,只需对很小的一部分区域重新划分网格,这大大减少了网格划分时间。
在计算方面,FRANC3D可以很好地将对接主流的有限元软件,如ABAQUS、ANSYS、MSC Mar等。求解时,直接调用有限元软件的求解器,充分利用了有限元软件的分析能力。软件分析流程,如图1所示。

图1 FRANC3D分析流程图Fig.1 FRANC3D Analysis Flowchart
FRANC3D提供两种方法计算应力强度因子,分别是M−积分法和位移相关法,其中位移相关法比较容易理解和实施,但精度较差,通常用于针对零部件的健康检查,但不适用于生产工作。M−积分是默认的方法,在数值上与J积分相似,拥有较高的求解精度。
这里选用M−积分求解裂纹。其表达式为[12]:
式中:Г—围绕裂纹尖端的积分回路;
M−积分与应力强度因子关系为:
式中:KI、KII、KIII—三种基本裂纹形式对应的应力强度因子。
由于大量的实验研究表明[13],在轮轨接触中,疲劳裂纹主要以张开型裂纹KI裂纹为主,所以主要以I型裂纹为研究对象,具体分析结果见第四节。
3 数值模型的建立
先利用有限元软件ABAQUS对无裂纹的轮轨接触模型进行应力分析,获得整个轮轨模型的应力分布情况,并确定最大Von−Mises应力的准确位置,即裂纹最容易萌生和扩展的区域。然后将应力分析结果导入FRANC3D进行裂纹扩展分析。
3.1 几何尺寸与材料参数
在SolidWorks中建立了真实的轮轨模型,车轮型面选用标准磨耗型LMA型踏面[14],轨道为我国普遍采用的标准UIC60 型轨道[15]。考虑轨底坡对接触面的影响,按照实际情况设置1/40的轨底坡。轮轨选用相同的材料参数:弹性模量E=210000MPa,泊松比v=0.3,弹塑性参数,如表1所示。假设轮轨间摩擦系数为0.3。

表1 材料弹塑性应力应变表Tab.1 Material Elastoplastic Stress and Strain Table
3.2 有限元模型和网格划分
由于结构尺寸和模型边界条件具有对称性,为减少计算量和更好的进行裂纹扩展行为观察,选取了1/4的车轮模型和局部的轨道模型进行仿真计算。使用ABAQUS 软件中单元类型为C3D8R的8节点六面体单元划分有限元模型,对接触区域部分进行了细化,最小网格尺寸为1mm。车轮模型共计64944个单元和69360个节点。轨道模型共计40012个单元和43993个节点。
对模型施加15t载荷,计算得到轮轨接触区域最大Mises为722.4MPa,最大应力所在区域的应力分布情况,如图2所示。结果与文献[16]误差不到5%,认为模型准确性可以接受,能够用于裂纹仿真计算。后面将以该区域作为子模型引入裂纹。

图2 最大应力所在区域的应力分布情况Fig.2 Stress Distribution in the Area Where the Maximum Stress is Located
3.3 求解应力强度因子
将计算结果对接到FRANC3D求解应力强度因子。此时,可以将模型切分成全局模型和最大应力所在区域的子模型。对子模型引入裂纹,以简化计算,裂纹为半椭圆形,如图3所示。
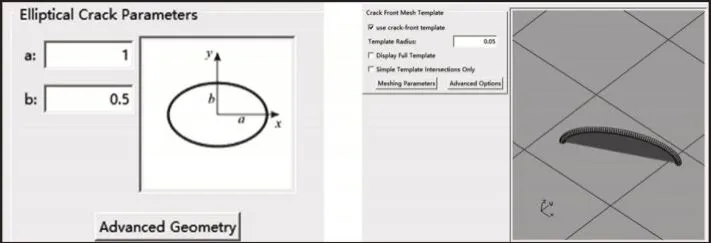
图3 引入裂纹Fig.3 Insert Crack
图3中裂纹长轴1mm,短轴0.5mm,裂纹深度8mm,裂纹角为30°。网格划分仅对裂纹区域的网格加密,保证了模型的完整性,也能更加精确地反映出裂纹特性。引入裂纹后轮轨子模型的网格图及其裂纹放大图,如图4所示。求解时,FRANC3D可以自动调用ABAQUS外部求解器。

图4 插入裂纹后的模型网格图及其裂纹放大图Fig.4 The Model Grid Diagram After Crack Insertion and the Enlarged View of the Crack
4 结果分析
4.1 裂纹长度的影响
在原模型的基础上保持短轴不变,改变长轴长度,使裂纹与踏面夹角呈30°,裂纹深度为8mm。FRANC3D计算的15t轴重下不同长度裂纹尖端3种应力强度因子数值模拟分布曲线,如图5所示。裂纹前缘被离散成许多点,图中横坐标轴采用量纲为1的裂纹前缘长度来表示裂纹因子所在的位置,即半椭圆形裂纹前缘上的裂纹点到起始点的弧长与整个弧长的比值。

图5 不同长度下的应力强度因子Fig.5 SIF at Different Lengths
由图中可知,在裂纹前缘两端,随着裂纹长度的增加,应力强度因子逐渐变小,中间段则相反,且裂纹长度超过0.5mm,应力强度因子增长速率加快,达到1mm时逐渐减慢。也就是说,随着裂纹长度的增大,裂纹两端与中间段的裂纹扩展速率有着不同趋势,中间段“先快后慢”,两端反之。
4.2 不同裂纹角的影响
保持裂纹长度及位置不变,改变原模型裂纹相对于垂直于踏面的角度,重新建立有限元模型,对所建立的模型进行计算分析,本文选取裂纹两端及中间处的三组数据,也就是0.002,0.5,0.998参量处,分别记为点11,22,33。后面也是针对该参量处数据进行研究。在裂纹的不同位置处,裂纹角对尖端应力强度因子的影响趋势相同,如图6所示。当裂纹角与踏面区呈30°时,裂纹尖端应力强度因子的值最大,说明此时的裂纹最容易扩展。当裂纹角从30°达到90°时,应力强度因子迅速减小,在与踏面垂直时取得最小值,此时裂纹相对安全。所以,应尽量避免出现小角度的裂纹。
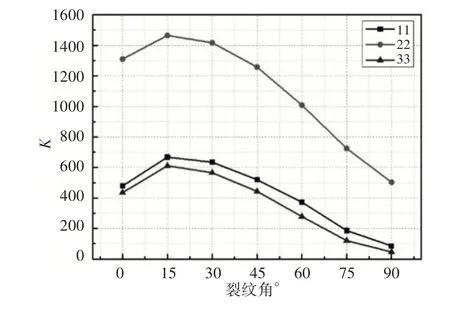
图6 不同裂纹角下的应力强度因子Fig.6 SIF at Different Crack Angles
4.3 不同载荷的影响
计算了裂纹尺寸1mm 的裂纹在不同轴重下的应力强度因子,如图7所示。对比三组数据,可以发现,各点处的应力强度因子随垂直负载几乎呈线性增加,且中间段的值明显高于两端。
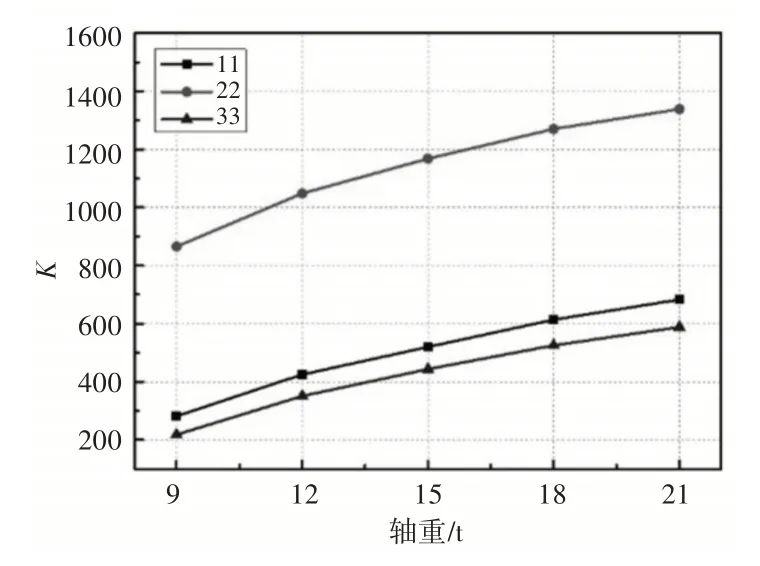
图7 不同轴重下的应力强度因子Fig.7 SIF at Different Axle Load
考虑到裂纹尺寸的影响,对了不同长度的裂纹在不同轴重下做了对比,如图8所示。对于不同长度的裂纹,应力强度因子同样随轴重线性增加,只是坡度略有变化。当载荷较小时,应力强度因子受裂纹长度影响较小,而当载荷较大时,应力强度因子随裂纹长度变化更为明显。所以列车在运行时应避免过载。
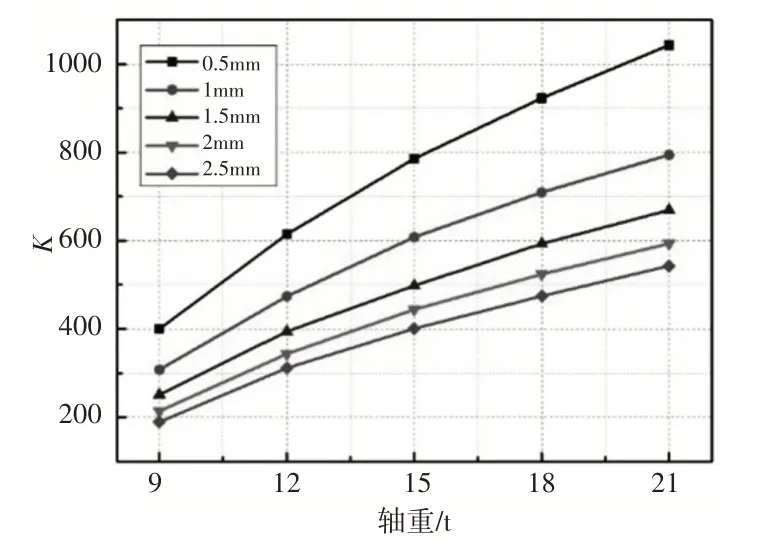
图8 不同裂纹长度下的应力强度因子随载荷变化图Fig.8 SIF Changes with Load Under Different Crack Lengths
4.4 不同裂纹位置的影响
保持原模型不变,建立不同深度的车轮踏面的内部裂纹,裂纹长度1mm,裂纹角为30°。轴重15t下裂纹尖端应力强度因子分布情况,如图9所示。从图中可知,在裂纹的各个位置处,应力强度因子随裂纹深度的增加先增大,后逐渐减小。为进一步探究规律,在ABAQUS中绘制了一条沿裂纹深度方向的路径,并提取了Mises应力分布情况,如图10所示。通过对比发现,应力强度因子K 与Mises 应力有着相似分布情况。由于此处为接触斑区域,此处的尖端应力和应力强度因子普遍较高,其他区域随着距离而逐渐减小。可见,接触斑对应力强度因子有显著的影响,处于接触斑附近的裂纹更容易扩展。

图9 不同裂纹深度下的应力强度因子Fig.9 SIF at Different Crack Depths
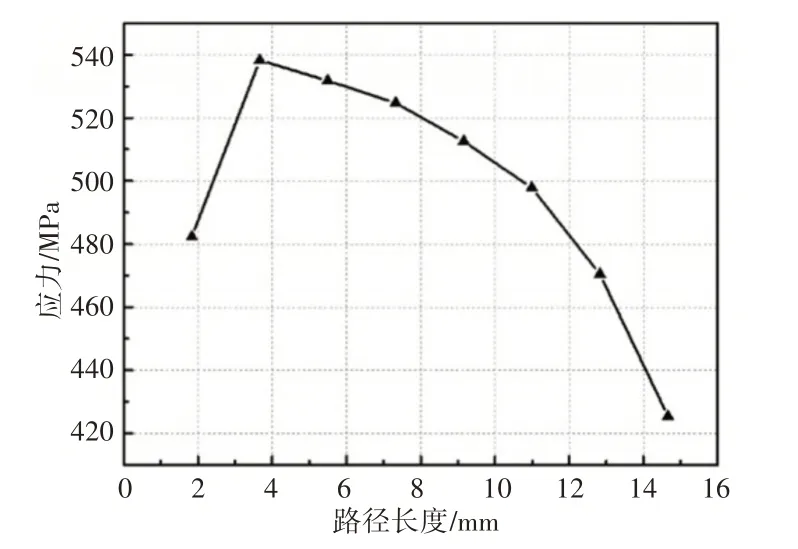
图10 沿路径方向的Mises应力分布Fig.10 Mises Stress Distribution Along the Path
5 结论
使用有限元软件ABAQUS 结合FRANC3D 软件研究了轮轨裂纹三维有限元模型的应力强度因子,探讨分析了不同工况下的裂纹与应力强度因子之间的关系。该方法更加方便地对裂纹尖端网格进行细化,省去了繁琐的部件切分工作,且结果可信度比较高。通过此软件的仿真模拟,可以得到如下结论:
(1)随着裂纹长度的增大,裂纹两端与中间段的裂纹扩展速率有着不同趋势,中间段“先快后慢”,两端反之。
(2)当裂纹角与踏面区呈30°时,裂纹裂尖应力强度因子的值最大,此时的裂纹最容易扩展。裂纹角从30°达到90°时,应力强度因子迅速减小,在与踏面垂直时取得最小值,此时裂纹相对安全。所以,应尽量避免出现小角度的裂纹。
(3)裂纹尖端应力强度因子随着垂直负载几乎呈线性增加。对于不同长度的裂纹,坡度略有变化。当载荷较小时,应力强度因子受裂纹长度影响较小,而当载荷较大时,应力强度因子随裂纹长度影响更为明显。所以列车在运行时应避免过载。
(4)应力强度因子随裂纹深度的增加先增大,后逐渐减小。且处于接触斑附近的裂纹更容易扩展。
