基于点云深度学习的对称结构空间目标相对位姿测量

王艺诗，徐田来，张泽旭，苏 宇

(哈尔滨工业大学航天学院深空探测基础研究中心，哈尔滨 150080)

0 引 言

空间目标相对位姿测量是在轨服务中的关键技术,精确的相对位姿测量能使航天器准确执行近距离机动并实现与空间目标的交会[1]。根据传感器的不同,空间目标相对位姿测量技术目前主要可分为基于相机和基于激光雷达两大类。在空间复杂环境下，基于图像的位姿测量方法受光照条件影响较大，过曝或过暗的图像都会影响相对位姿的准确求解，且仅利用图像观测目标三维运动状态会导致深度信息的丢失[2]。相比之下，激光雷达由于其在外空环境中被证明的鲁棒性而受到青睐[3]。激光雷达的观测不受空间光照条件影响，且激光雷达扫描的点云数据可以提供空间目标的三维结构信息。因此，基于激光点云的空间目标位姿测量技术具有显著的应用前景。

基于激光点云的相对位姿求解，传统方法是采用ICP(最近点迭代)算法，通过迭代点云最近点的方法解算目标相对位姿。然而ICP算法对初值要求较高[4]，且当点云密集时计算量较大，不利于保证位姿测量的时效性。另外，一些研究者设计了人工编码特征用于描述点云的局部几何结构,这种基于点云特征的配准方法可以作为粗配准,为ICP迭代计算提供良好初值，但这种方法容易受到噪声、异常点的影响,特征匹配效率不高[5]。同时考虑到空间目标可能具有的高度对称结构，如典型的通信卫星都具有两个对称的太阳帆板等，仅使用ICP算法进行点云配准极有可能将其误匹配到模型的另一对称部分，进而导致位姿求解误差。并且这种具有对称结构的目标在进行点云配准时，对称部位计算的人工编码特征也高度相似，两组点云3D和3D的位置关系不再具有一一对应的特征，这为姿态的求解带来了挑战。

深度学习方法的兴起给目标位姿测量问题提供了新的解决思路。深度学习已成功应用于解决各种二维图像问题，一些学者以视觉图像作为数据输入，针对对称结构目标引起的位姿估计模糊问题，提出了许多基于深度学习网络的目标位姿测量方法。其中Rad等[6]假设全局物体对称性已知，提出了一种适用于对称轴投影近似垂直的物体的位姿归一化方法。Yu等[7]提出了PoseCNN位姿估计网络,优化了一种全局对象对称性不变的损失函数。Kehl等[8]设计了SSD-6D网络，提出一种针对目标对称性定义的视点子集训练分类器。相较于深度学习在图像处理中的成功应用，基于点云的深度学习仍处于起步阶段。点云是无序点的集合，无法直接应用卷积操作；同时，点云采样密度不均匀很难保证特征学习的鲁棒性，增加了将深度学习应用于点云数据的难度[9]，并且无结构的点云数据直接输入到卷积神经网络中往往比较困难。因此将深度学习应用于点云数据中，需要解决点云无序性、稀疏性等难题。

Qi等[10]提出的PointNet网络作为点云深度学习研究的先驱者为点云深度学习提供了新的方法。它将原始点云直接输入网络，通过多层感知机(MLP)分别学习点云中每个点的特征，然后用对称函数(最大池化层)来解决点云无序性问题[5]。作为点云深度学习的开创性工作，PointNet网络在点云分类和语义分割任务中取得了良好成绩。目前，将基于点云数据的深度学习与相对位姿求解结合在一起的研究相对较少。针对这一问题，陈海永等[11]提出一种针对复杂场景点云数据的多层特征姿态估计网络(MFPE-Net)有效解决了机器人抓取过程中的位姿估计问题。Gao等[12]提出了一种基于激光点云数据的6D位姿估计网络CloudPose，该网络可用无序点云分别估计目标的平移和旋转向量。肖仕华等[9]设计了一种基于深度学习的三维点云头部姿态估计网络HPENet。该网络采用多层感知器和最大池化层实现点云的特征提取，并通过全连接层输出预测的头部姿态，网络估计的姿态准确度和计算的复杂度有较好的性能。Gao等[13]提出了一种基于点云深度的目标6D位姿估计网络CloudAAE，该网络在点云的特征提取部分引入了EdgeConv边卷积算法，相较于CloudPose，CloudAAE网络提高了对点云局部特征的学习能力。

本文提出一种基于点云深度学习的对称结构空间目标相对位姿测量方法。首先采用Pointwise-CNN中的逐点卷积算法来提取点云特征，然后采用最大池化层来解决点云无序性问题，同时最大池化层输出点云全局特征。考虑空间目标激光点云为具有时域关系的序列化点云，引入长短时记忆网络LSTM来学习序列点云之间的长期依赖关系。提取到点云特征以后，进一步构建两个并行的回归网络分别输出空间目标平移向量和具有固定标签的目标点云三维边界框角点。根据相同的标签编号确定两组点云三维边界框角点的匹配关系并求解点云相对姿态，避免了通过迭代最近点的方式寻找点云匹配关系，可有效解决对称结构空间目标点云误配准导致的姿态求解误差问题。

1 点云深度学习网络

1.1 网络架构设计

图1为深度学习网络Lasernet整体架构设计。网络主要分为两部分，包括点云特征提取网络与关键点回归网络。输入网络的空间目标点云经特征提取网络进行深层次高维表征后，将提取的特征输入由三层全连接层构成的回归网络。回归网络使用两个并行的网络来分别估计平移向量和具有固定标签的目标点云三维边界框角点。其中一个回归网络直接输出空间目标的平移向量。另一个回归网络考虑到旋转空间的非线性，直接用网络回归四元数姿态的方法泛化能力较差，所以采用间接法来估计目标姿态。网络输出空间目标点云的关键点，三维点云数据中关键点通常选择三维边界框的8个角点，网络输出的每一个角点具有固定的标签(如图5所示)。进一步基于最小二乘法，由网络输出的带有固定标签的三维边界框角点来间接计算空间目标点云的姿态。

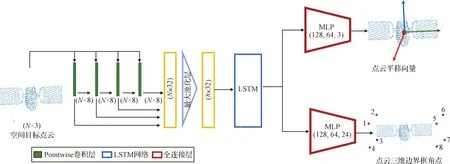
图1 深度学习网络Lasernet整体架构Fig.1 Model design for the Lasernet deep learning network

1.2 点云特征提取网络

网络直接以仅有三维坐标的空间目标点云数据作为输入，输入网络的张量维度为H×B×N×C，其中B是输入批处理的大小，N为输入点云的点数，C为点云的通道数。本文输入仅有三维坐标的点云，即C的值为3。由于本文采用了长短时记忆网络(LSTM)，所以输入维度中H为序列长度。为了能够更好的回归点云关键点，需要充分学习点云局部特征和全局特征信息。相较于PointNet网络仅采用三层一维卷积单纯地为点云中的点做几何特征维度上的扩展，从而丢失每个点与其周边领域内的局部特征。本文采用Pointwise-CNN网络[14]中提出的一种新的逐点卷积核提取点云特征，来提升网络对点云局部特征的学习能力[15]。

Pointwise-CNN逐点卷积核以输入点云中的某一点为中心，将邻近点划分为核单元，卷积核中的相邻点都参与运算，并在整个点云中滑动进行卷积，由此可对点云局部特征进行学习。每个卷积核都有一个半径值，可以根据每个卷积层中不同数量的相邻点进行调整，如图2所示。

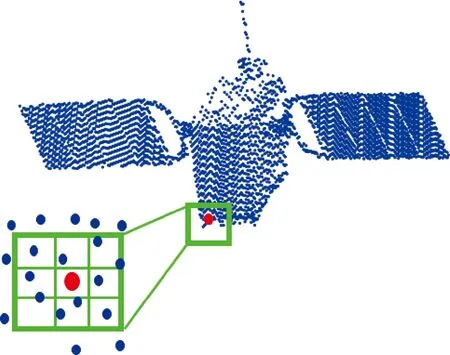
图2 Pointwise-CNN逐点卷积Fig.2 Pointwise-CNN：convolution operator that can be applied at each point of a point cloud

逐点卷积使用3×3×3的卷积核，每个卷积核区域内的所有点有相同的权重。逐点卷积核表示如下[14]：

(1)

式中：Ωi(k)表示以点i为中心的卷积核第k个子域；pi是第i点的坐标；ωk表示卷积核中第k个子域的权重；xi和xj是点i和点j的值，-1和表示输入层和输出层的索引。

使用四层Pointwise逐点卷积层提取点云特征，每一层后面都有一个SELU激活函数。将每一层输出的点云特征连接起来，然后输入进最大池化层。进一步为了有效地使用序列点云的时序信息，将序列为H的点云特征输入进长短时记忆网络LSTM。作为循环网络RNN的改进模型，LSTM引入了门控机制，遗忘门决定内部状态是否将前一时刻的不相关信息丢弃，输入门决定当前时刻保存多少新输入的信息。LSTM的记忆单元提供了连续帧数据的相关性，并且避免了当输入序列较长时，网络模型存在的梯度消失问题。提取到点云高层抽象特征后，使用关键点回归网络来分别回归点云平移向量和具有固定标签的点云三维边界框角点。

1.3 关键点回归网络

将空间目标位姿测量问题转换为点云关键点回归问题来处理，设计了基于回归模型的关键点映射网络。特征提取网络对空间目标点云进行深层次高维表征后，利用三层全连接层构成的MLP感知器分别回归点云平移向量和具有固定标签的点云三维边界框的8个角点。回归网络如图3所示，网络在构建时前两层全连接层都连接Softsign激活函数，最后一层全连接层不加激活函数。Softsign激活函数返回-1和1之间的值，其更平坦的曲线与更慢的下降导数表明它可以更高效地学习，且能够更好地解决梯度消失问题;同时为了防止过拟合，加入了Dropout操作(σ=0.5)。

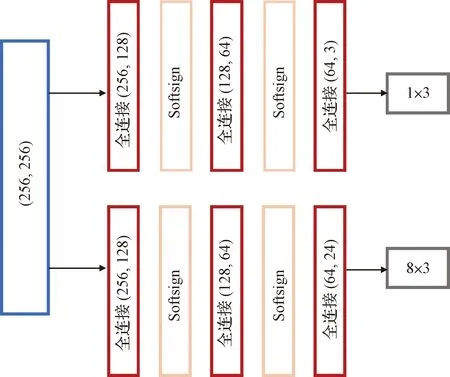
图3 关键点回归网络Fig.3 Regression network of key points

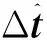
(2)

(3)

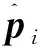
(4)

2 基于固定标签角点的目标相对姿态估计

本节利用网络输出的带有连续稳定标签的点云三维边界框角点求解目标姿态。网络在训练点云三维边界框的角点时，将真实的三维边界框的角点按照从1至8的固定顺序编号(如图4所示)，则网络估计的8个角点也将按照相同的固定顺序输出，如此得到的三维边界框的每一个角点带有一个如图4所示的固定标签。

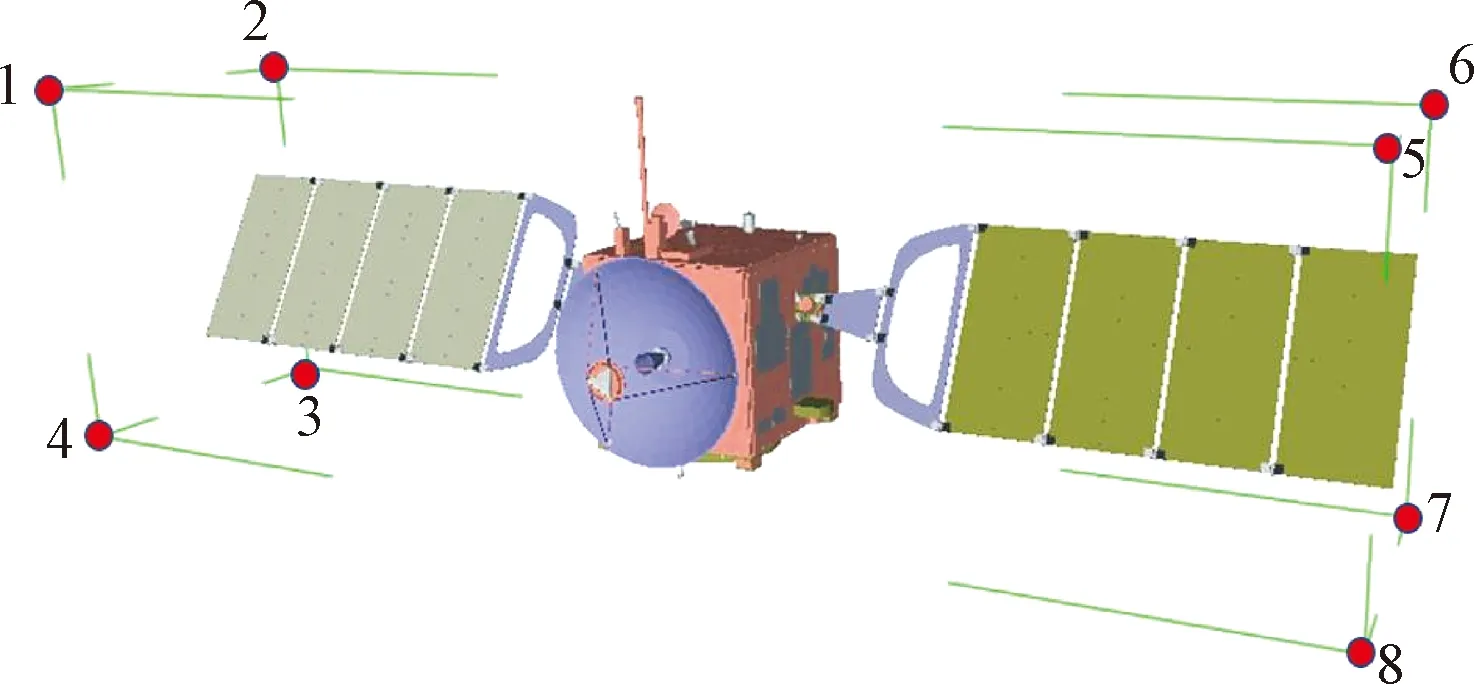
图4 带有固定标签的三维边界框角点Fig.4 3D bounding box corners with fixed labels

针对对称结构空间目标相对位姿求解问题，传统算法(如ICP算法)，仅利用迭代点云最近点的方法寻找两点云的匹配关系时，当前帧点云配准极易匹配到模型的另一对称部分或对称角造成点云误匹配从而导致姿态求解错误。如图5(a)所示，结构对称的点云配准到了目标点云的对称面，这将导致姿态求解时与真实姿态相差180°。

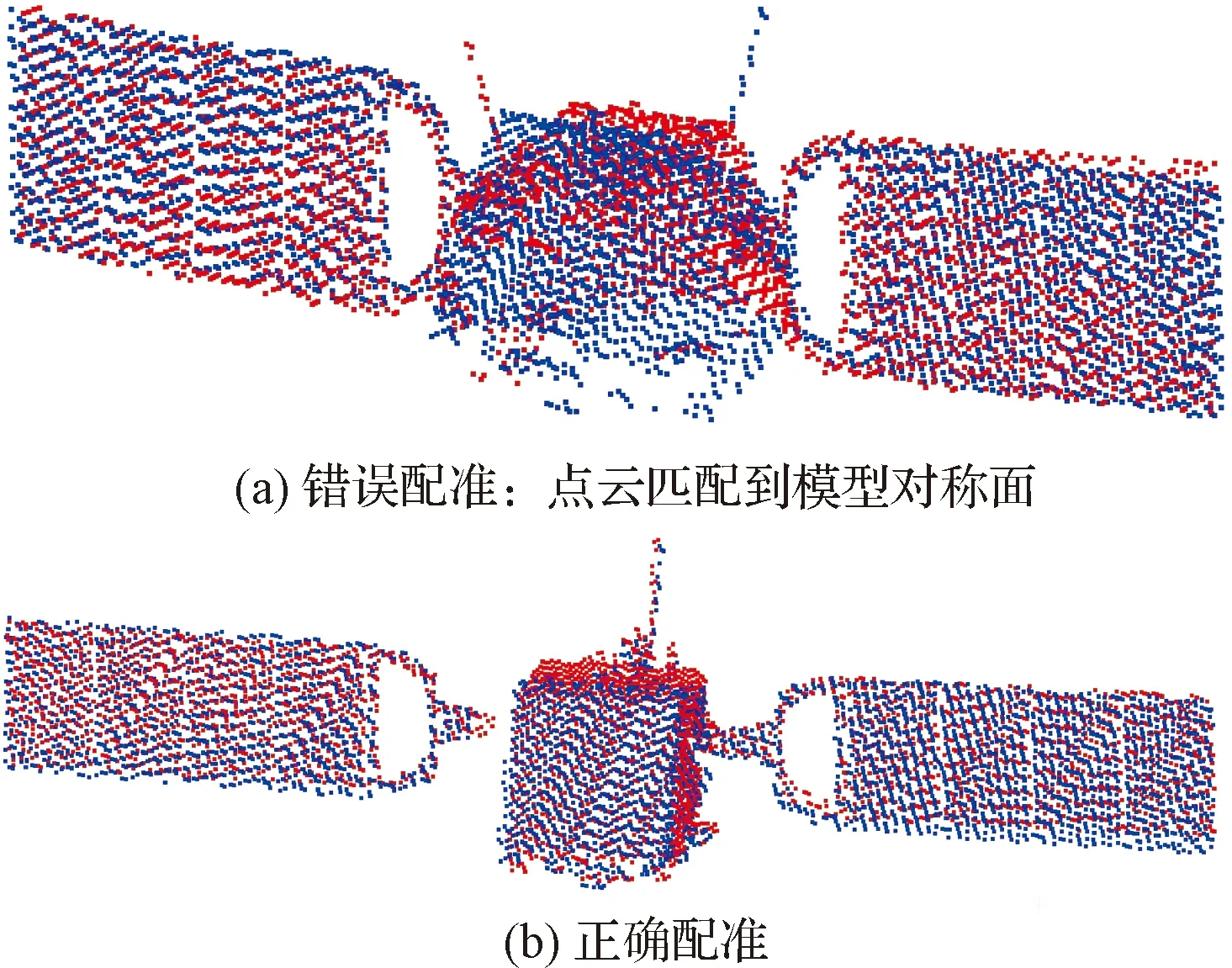
图5 空间目标对称结构点云配准误匹配Fig.5 The symmetric structure of space objects leads to mismatching of point cloud registration

相较于传统算法仅根据两组点云中点对的最近距离进行点云配准，网络输出的带有固定标签的三维边界框的8个角点，根据相同的标签编号确定两组点云中匹配的关键点对，避免了通过迭代最近点的方式寻找点云匹配关系。两组点云利用标签相对应的角点求解姿态可有效解决对称结构空间目标点云误配准导致的姿态求解错误问题。

定义惯性坐标系O-xyz，目标本体坐标系Ot-xtytzt，服务航天器坐标系Os-xsyszs，如图6所示。

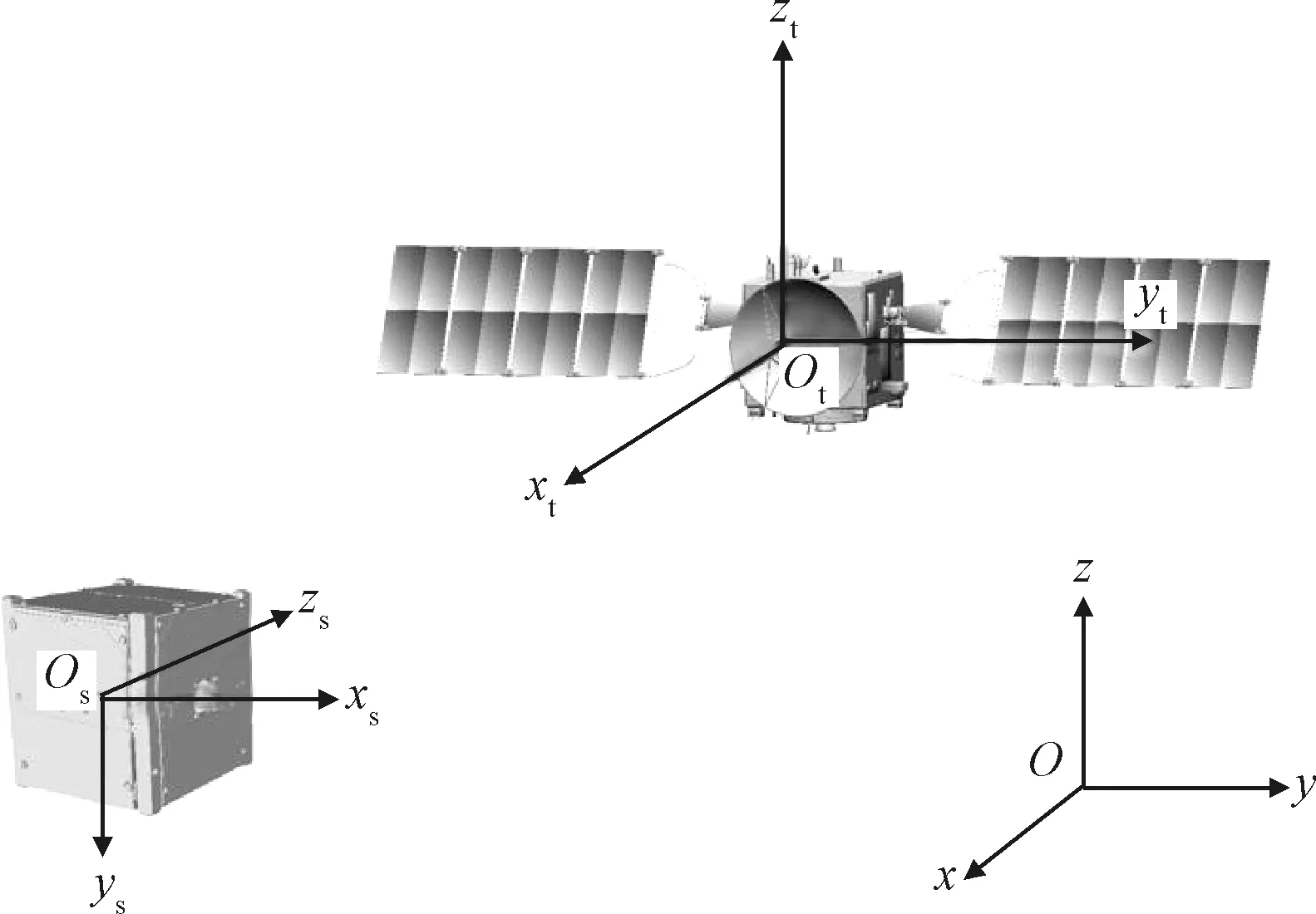
图6 坐标系定义Fig.6 Coordinate system definition

绕三轴的滚转、偏航、俯仰旋转矩阵分别为Rx,Ry,Rz。

(5)

(6)

(7)

式中：φ,φ,θ分别为滚转、偏航、俯仰角度。三维旋转矩阵R(φ,φ,θ)可表示为：

R(φ,φ,θ)=RxRyRz

(8)

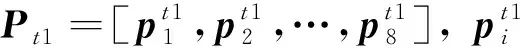
(9)

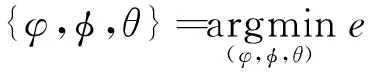
(10)

基于固定标签的三维边界框角点由公式(10)可求得空间目标的相对运动姿态φ,φ,θ。

3 仿真实验与分析

3.1 目标仿真数据集

针对某型号空间目标模型建立激光点云数据集。利用Unity模拟三维激光雷达，设置64线激光雷达，激光扫描仪视场为20°，目标最大直径为14 m记为d，目标主体长4 m、宽4 m、高4.5 m。设置目标相对激光雷达的深度运动范围为5d～20d，即目标的深度运动范围为70 m至280 m。如图7所示，图中红色区域为空间目标相对激光雷达的运动范围。仿真得到400组序列点云，每组序列点云在目标运动范围内的初始位置随机选取，每组序列中有100帧具有连续运动位姿的激光点云，共获得40000帧空间目标激光点云。将其中350组点云作为训练集，50组点云作为测试集。考虑点云仿真过程中随着目标深度的变化，目标大小会导致点云密度的不同，因此在将点云输入进网络前，会对点云进行均匀采样，保证所有点云包含的点数相同，且为了网络更好的进行训练，将点云数据归一化到[-1,1]区间内。

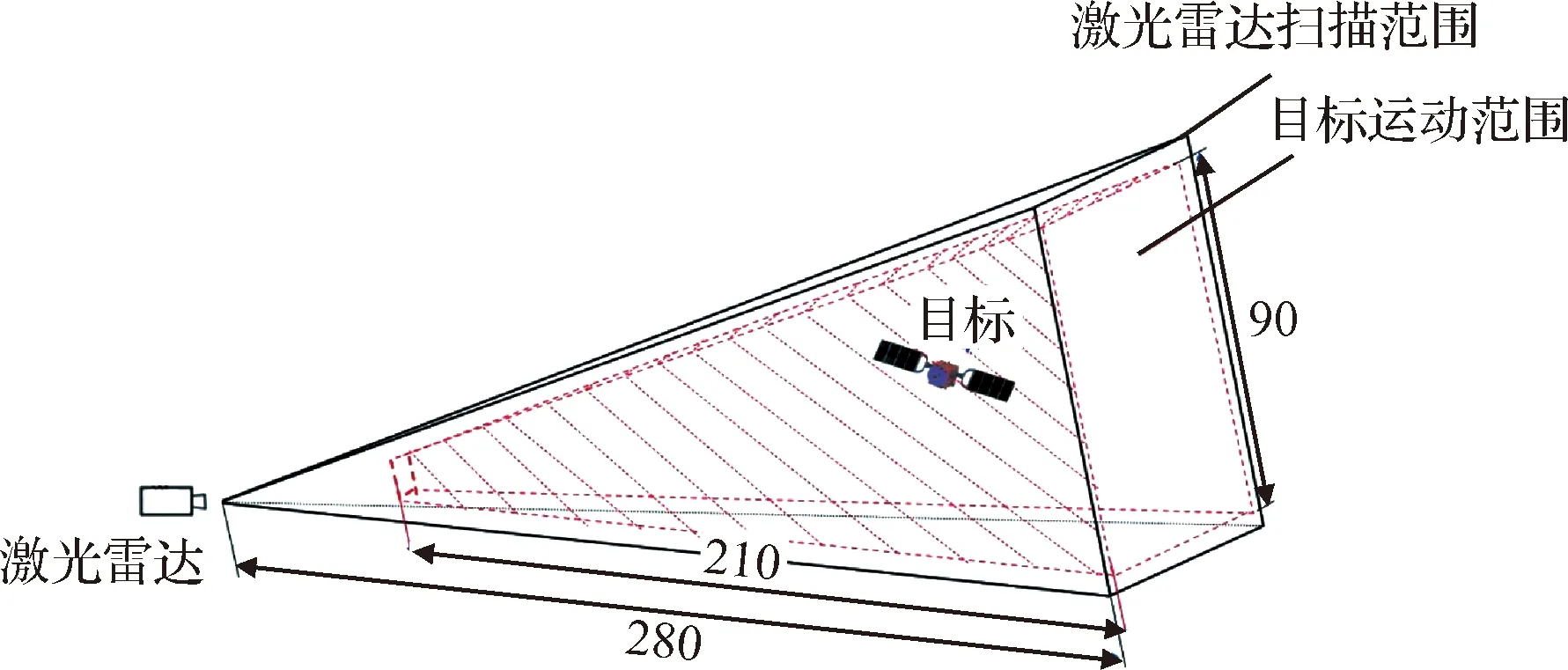
图7 激光点云仿真工况Fig.7 Laser point cloud simulation conditions

3.2 网络训练环境及参数设置

深度学习模型训练基于Ubuntu 18.04操作系统，CPU为Intel Core-i7(3.40 GHz)，内存为16 GB，显卡为NVIDIA GTX3060 12 GB。设置网络超参数，批处理batch的大小为16，LSTM网络序列H为10，输入点云的点数均为800，初始学习率为0.0001，衰减率为0.1，每训练数据集的50%, 80%, 90%调节学习率下降0.1倍。迭代训练次数为10000次。训练选用ADAM优化器，相比于其他经典的优化器，ADAM优化器在更新参数时学习率能够具有自适应性，使得网络在训练时具有更好的鲁棒性与学习率的动态调整性能。

3.3 评价标准

点云三维边界框的8个角点的误差计算，依据预测的8个角点与对应的真实8个角点的的距离可得：

(11)

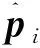
对于位姿估计常用的评价指标是平均点对距离ADD，即将3D模型点云分别做真实位姿和预测位姿的刚体变换后求点对的平均欧氏距离。

(12)

3.4 结果与误差分析

网络输出得到的空间目标平移向量三轴误差如图8所示。以一个序列中的100帧点云为例，对于目标深度运动范围为70 m至170 m的工况，平移向量三轴误差均小于0.8 m。对于全部测试集5000帧目标点云，空间目标平移向量三轴误差小于1 m的占比为86%。

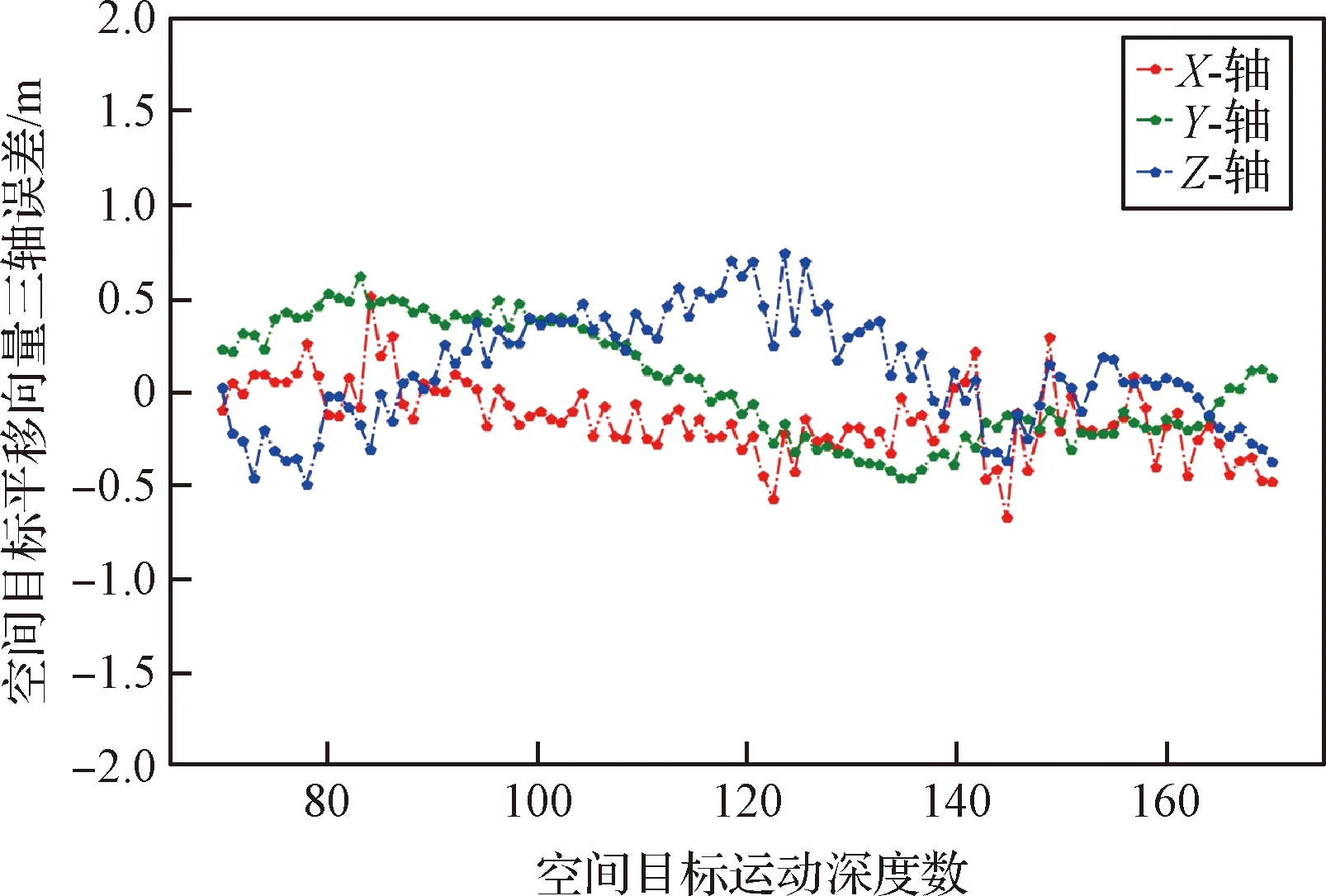
图8 空间目标平移向量三轴误差Fig.8 Three-axis errors in the translation vector of the space target

网络输出得到的带有稳定标签的点云三维边界框角点如图9所示，对网络输出的8个角点的距离误差进行评估，以一个序列中的100帧点云为例，精度评估结果如图10所示，对于最大直径14 m的空间目标，网络预测的8个角点的误差均小于0.3 m。对于全部测试集5000帧目标点云，点云三维边界框角点预测的误差小于0.5 m的占比为85%。

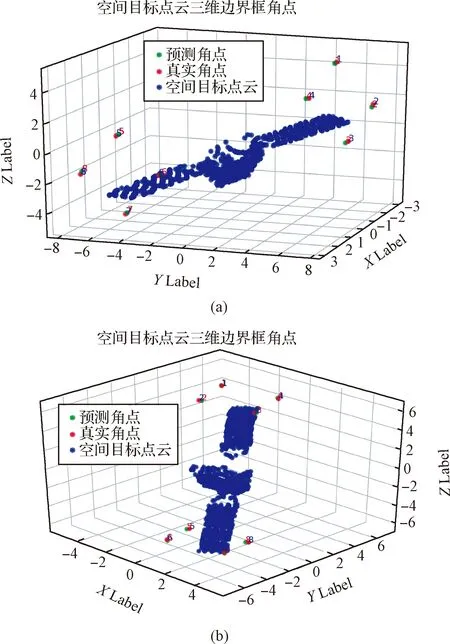
图9 不同姿态下点云三维边界框角点Fig.9 3D bounding box corners of point clouds with different rotations

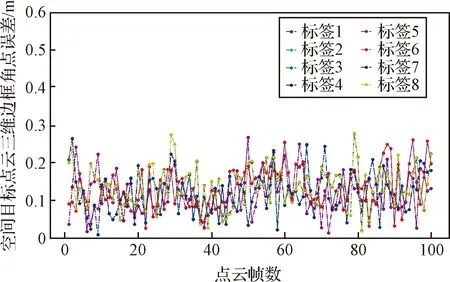
图10 空间目标点云三维边界框角点误差Fig.10 Error of 3D bounding box corners ofthe of the space target point clouds

利用带有连续稳定标签的点云三维边界框角点求解空间目标姿态。以一个序列中的点云为例，空间目标姿态的三轴误差均小于2.76°，如图11所示。对于全部测试集5000帧目标点云，空间目标姿态的三轴误差小于5°的占比为89%。

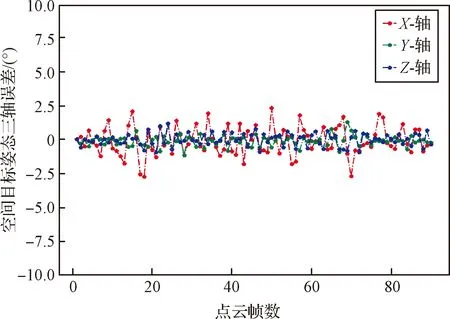
图11 空间目标姿态测量三轴误差Fig.11 Three-axis errors in the attitude measurement of the space target

利用本文所提方法测量的空间目标位姿，计算空间目标点云平均点对距离误差如图12所示。以一个序列中的点云为例，对于最大直径为14 m的空间目标，点云的平均点对距离误差均小于0.8 m。

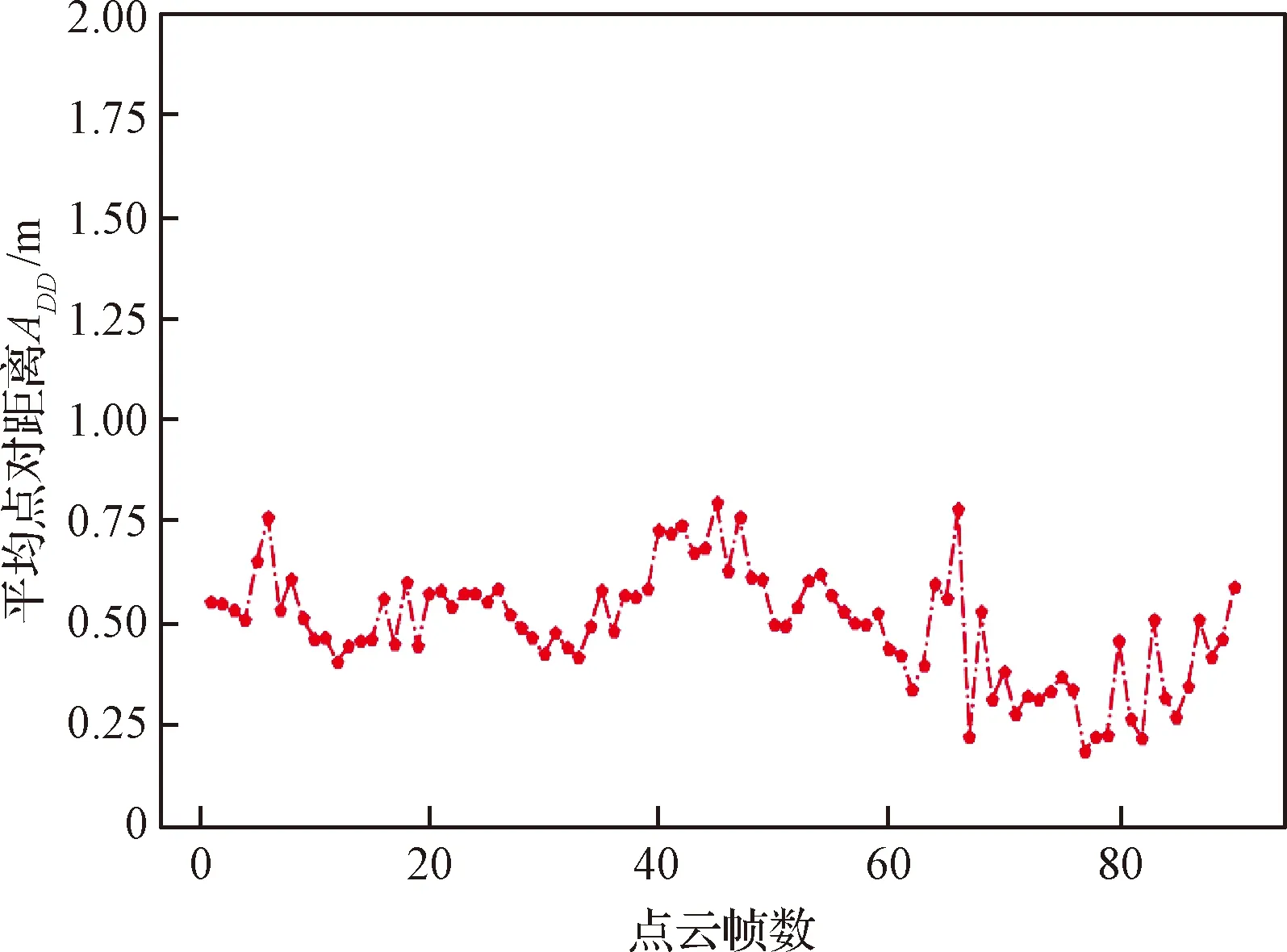
图12 空间目标位姿测量ADD评估精度Fig.12 ADD evaluation accuracy of the space target pose

图13显示了将空间目标点云分别基于计算得到的位姿和基于真实的位姿变换回场景中的点云配准效果。蓝色点云由计算所得位姿转换得到，红色点云由真实位姿转换得到，可以看出两组点云基本重合。

本文将所提出的方法与传统点云ICP配准方法和其他基于点云深度学习的方法进行对比：分别采用FPFH+ICP, CloudPose和CloudAAE三种方法作为对比实验。其中第一种是在传统的基于人工描述子的ICP配准方法中常用的位姿测量方法。第二种方法CloudPose是基于点云深度学习直接输出位姿的网络训练方法。第三种方法CloudAAE在网络的特征提取部分引入一种边卷积算法EdgeConv，使网络能够更好地学习到点云的局部特征。如表1所示是上述几种方法的空间目标位姿测量ADD评估准确率和姿态角误差小于5°，平移向量误差小于1 m所占比率。位姿测量的预测评估，通常表示为点云平均点对距离误差ADD小于目标最大直径10%的度量准确率。可以看到相比其他方法，本文所提出的方法准确率明显更高。

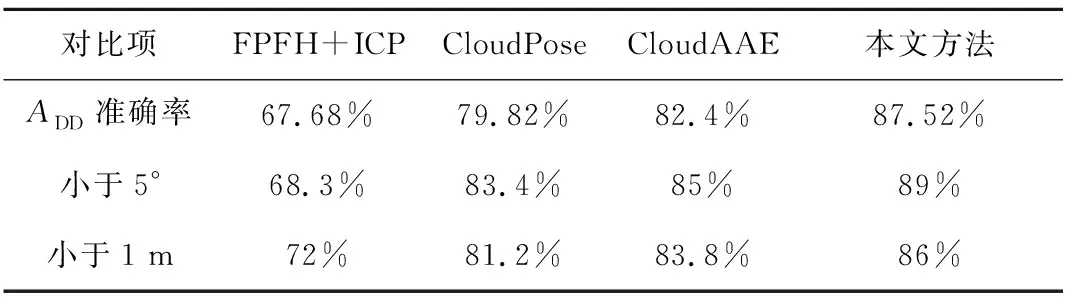
表1 位姿测量准确率对比实验Table 1 Comparative experiments on the accuracy of pose measurement

4 结 论

本文针对现有方法在解决几何结构高度对称的空间目标点云位姿测量问题中存在的误匹配问题，提出一种基于点云深度学习的相对位姿测量方法。网络以点云坐标作为输入，经过特征提取网络及关键点回归网络分别输出空间目标平移向量和具有固定标签的目标点云三维边界框角点。利用带有连续稳定标签的角点求解目标姿态，可有效避免目标对称结构带来的点云误匹配问题。经仿真实验验证，本文提出的方法得到的空间目标位姿误差较小，相较于对比实验中的其他三种方法在整体精度上具有明显优势。