导轨间距变化的电磁感应创新问题探究

刘文娟

(甘肃省民乐县第一中学)

高考的考查已经从“解题”向“解决问题”转化.解决问题不仅指向经典试题的求解,更追求原创试题的求解.解决原创试题,需要清楚物理原创题的由来.本文以一类基本的电磁感应问题谈物理试题的创新.

1 等间距导轨变为间距逐渐变化导轨

例1如图1所示,互相垂直的两根光滑足够长金属轨道POQ固定在水平面内,电阻不计.轨道内存在磁感应强度为B、方向竖直向下的匀强磁场.一根质量为m、单位长度电阻值为r0的长金属杆MN与轨道成45°角放置在轨道上.以O位置为坐标原点,t＝0时刻起,杆MN在水平向右的外力作用下,从O点沿x轴以速度v0匀速向右运动.求:

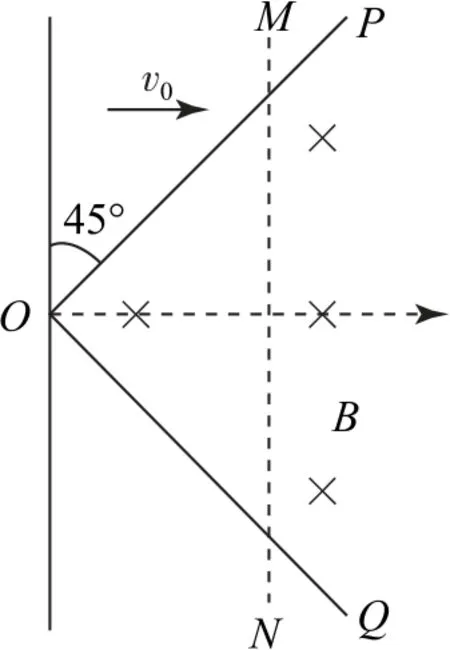
图1

(1)t时刻MN中电流I的大小和方向;

(2)t时间内,MN上产生的热量Q;

(3)写出外力F与时间t关系的表达式.

(3)由匀速运动可知

点评当两导轨间距变化时,由于导体棒匀速运动,因此产生的电动势均匀增加,导体棒的电阻也在均匀增加,可以推导回路电流不变,进而可以推出安培力随时间均匀增加,导体棒上的发热量随时间的平方均匀增加.本题也可以选择题的形式命制,借助图像,考查电流随时间、安培力随时间、发热功率随时间、总发热量随时间的变化规律.

2 等间距导轨变为间距突变导轨

例2如图2所示,光滑的平行金属导轨固定在绝缘水平面上,导轨处在垂直于水平面向下的匀强磁场中,左侧导轨间的距离为2L,右侧导轨间的距离为L,导体棒a、b垂直放置于导轨之间,且与导轨接触良好,导体棒a的质量是b的质量的4倍,电阻相等.第一次将导体棒b固定在右侧导轨上,使导体棒a以初速度v0开始向右运动,直至回路中的感应电流变为0.第二次导体棒b未被固定且静止在右侧导轨上,使导体棒a仍以初速度v0开始向右运动,直至回路中的感应电流也变为0.已知前后两次回路中的感应电流变为0时,导体棒a仍处在左侧导轨上,不计导轨的电阻.下列说法正确的是( ).

图2

A.第二次导体棒a和导体棒b组成的系统动量不守恒

B.第一次回路中产生的焦耳热是第二次的9倍

C.第一次通过回路的电荷量是第二次的2倍

D.第一次导体棒a动量的变化量是第二次的5倍

分析第二次导体棒b未被固定,导体棒a向右减速,导体棒b向右加速,终极状态B·2Lva＝BLvb,在该过程中,导体棒a和b中的电流始终相等,由F＝BIL可知,导体棒a所受安培力为导体棒b所受安培力的2倍,系统动量不守恒,选项A 正确;第一次将导体棒b固定在右侧导轨上,则导体棒a速度最终减为0,由于导体棒a、b的电阻相等,故可设b棒质量为m,则a棒质量为4m,第一次回路中产生的焦耳热是,第二次由动量定理有4m(v0-va)＝2mvb,解得,回路内的发热量为

故第一次回路中产生的焦耳热是第二次的2倍,选项B错误;第一次导体棒a动量的变化量大小为4mv0,第二次导体棒a动量的变化量大小为2mv0,故第一次导体棒a动量的变化量是第二次的2倍,选项D 错误;根据Bq·2L＝4mv0,Bq′·2L＝2mv0,可知第一次通过回路的电荷量是第二次的2倍,选项C正确.

点评本题在两导体棒长度不等的背景下考查了导体棒b固定和不固定两种情境.分析两导体棒的最终状态是解决问题的关键,动量定理是解决问题的方法.物理情境虽然变化了,但解决问题的思路和方法不变.

3 导轨间距不断变化的组合模型

例3如图3所示,匀强磁场垂直于纸面向外且范围足够大,磁感应强度的大小为B＝3T,水平面上固定不计电阻的关于Ox对称的足够长的轨道OABCD和OEFGH.其中EF∥AB且间距为L＝,OE、OA与Ox轴的夹角均为θ,且θ＝30°.

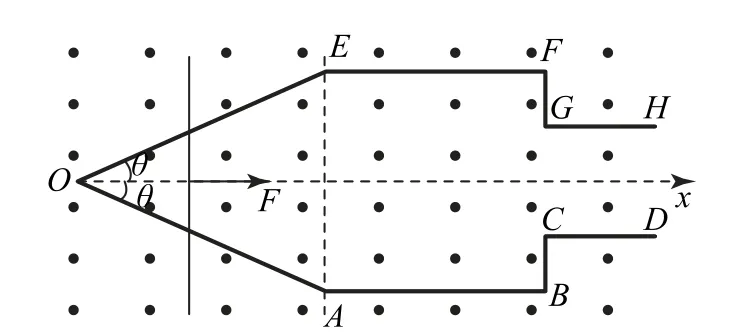
图3

一根粗细均匀的导体棒长度为L,质量为m＝6kg,单位长度的电阻为r＝3Ω,用沿着x轴正方向向右的拉力F作用在导体棒的中点,使其从O点开始沿着Ox轴做匀速直线运动,速度的大小为v0＝2m·s-1.3s末撤去拉力,同时断开OE和OA的连接,且在GH和CD导轨的左端放一根质量为、长度为的导体棒,金属棒与导轨接触良好,不计一切摩擦.求:

(1)导体棒在EOA轨道上时,电流的大小;

(2)导体棒在EOA轨道上运动过程中,产生的焦耳热;

(3)EF和GH都足够长,3s末之后两棒产生的总焦耳热.

分析(1)设切割磁感线的导体棒长度为d,则有,联立可得I＝2A.

(2)导体棒在EOA轨道上运动过程中,移动的距离为x＝v0t,d＝2xtan30°.可得t＝3s,x＝6 m,则导体棒的有效电阻为R′＝r·2v0ttan30°,可知电阻与时间成正比,则最大电阻为,则导体棒在EOA轨道上运动过程中,产生的焦耳热

点评本题组合了导轨间距逐渐变化和导轨间距突变两种模型,即综合了例1和例2两种模型,解决两种模型的方法不变,导体棒间距变化的轨道进入间距不变轨道的瞬间速度不变是解决问题的切入点.

由以上问题可以看出,物理创新试题可改换物理条件进行物理模型的创新,也可以对物理模型进行重组创新出组合模型.解决物理创新试题,要以变的因素为入手点,利用原有的物理方法进行解题.熟练掌握物理基础知识是解决问题的前提,把握物理模型间的内在联系是解决问题的关键.

(完)