阵元位置误差下的嵌套阵列DOA 估计方法

贺 顺, 贺小艳, 杨志伟, 孙 兵, 谢永妮

(1. 西安科技大学 通信与信息工程学院, 陕西 西安 710600;2. 西安电子科技大学 雷达信号处理国家重点实验室, 陕西 西安 710071;3. 中国卫星海上测控部, 江苏 江阴 214430)

0 引言

波达方向(Direction of Arrival,DOA)估计是阵列信号处理的重要内容,被广泛应用于声纳、雷达和无线通信等领域[1-3]。 嵌套阵列是一种经典稀疏阵列,通过均匀线阵和稀疏阵列组合的灵活布阵方式,从而提高阵列的自由度和孔径[4-5]。 然而,在实际工程应用中,由于阵元位置误差不可避免,阵列流型存在一定的偏差或扰动,导致基于嵌套阵列的DOA估计方法性能严重恶化甚至失效[6-8]。

阵元位置误差的校正方法主要分为2 大类:第1 类为自校正方法[9-10],这类方法通过构造优化函数,联合优化求解阵元位置误差和信源方位;第2类是有源校正算法[11-13],通过在空间中人为放置方位已知的校正源实现阵元位置误差的校正。 文献[12]在假设校正源方位已知情况下,提出迭代最大似然校正算法,有效提高角度估计精度。 文献[13]提出改进的迭代最大似然算法,能够进一步提高DOA 估计精度,但在小快拍情况下性能不佳。近年来,稀疏重构对强噪声具有良好鲁棒性,引起了国内外学者的广泛关注[14-16],同时为阵元位置误差校正算法提供了新的研究思路。 文献[17]结合阵元位置稀疏特性和压缩感知理论,提出适用于任意阵型的L1-SVD 方法,但存在基不匹配问题,使得阵元位置估计性能下降。 文献[18]进行Toeplitz 预处理后,采用优化后的核范数恢复算法得到协方差矩阵,该方法能够避免因网格离散化处理产生的基不匹配问题,同时有效提升阵元位置误差下的DOA 估计性能,但易受阵元位置误差的影响。

针对上述问题,在嵌套阵列基础上,本文提出了一种基于阵列流型分离的最小原子范数DOA 估计方法。 通过单辅助信源估计实际阵元位置,并建立阵元位置误差情况下嵌套阵列的虚拟域接收信号模型,再利用AMS-ANM 方法分离阵列流型中的位置信息和角度信息,并且求解最小原子范数问题,最后结合root-music 方法进行DOA 估计。

1 嵌套阵列信号模型

1.1 理想条件下的信号模型

理想条件下的嵌套阵列结构图如图1 所示。 嵌套阵列由2 个均匀线性子阵组成,均匀子阵1 包含N个阵元,阵元间距为d1,均匀子阵2 包含M个阵元,阵元间距为d2=(N+1)d1,其中N和M是整数,d1=d=λ/2 为半波长。

图1 嵌套阵列结构Fig.1 Geometry structure of nested array

以第一个阵元为参考阵元,阵元位置集合PNA为:

假设有K个互不相关的远场窄带信号入射到嵌套阵列上,其入射角度为θ=[θ0,θ1,…,θK-1]。 则嵌套阵列接收信号的第l个快拍为:

式中,x(l)= [x0(l),x1(l),…,xN+M-1(l)]T为接收信号矢量;s(l)= [s0(l),s1(l),…,sK-1(l)]T为源信号矢量;A=[a(θ0)a(θ1) …a(θK-1)]为阵列流型矩阵;a(θk)= [ej2πP0cosθk/λ,ej2πP1cosθk/λ,…,ej2πPN+M-1cosθk/λ]T为导向矢量,其中,Pq为集合PNA中第q +1 个元素;n(l) 为高斯白噪声矢量。

1.2 阵元位置误差模型

导向矢量可写为:

式中,°表示Schur-Hadamard 积;Γ(θk) 为阵元位置误差导致的相位扰动矩阵。

阵元位置误差下的阵列流型矩阵和接收信号的矢量形式为:

则嵌套阵列L个快拍下接收数据的协方差矩阵为:

2 阵元位置误差校正与DOA 估计

2.1 阵元位置误差估计

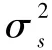
由此可得第q +1 个阵元位置误差的估计值为:

式中, angle(·) 代表求相位。

通过求解各个阵元位置误差Δ,可得嵌套阵列实际阵元位置集合为:

2.2 虚拟阵列生成

为了充分利用嵌套阵列自由度优势,对接收数据协方差矩阵进行向量化操作,得到差分联合阵列的接收数据:

差分联合阵列的集合可以表示为:

理想情况下,通过去除重复位置差得到虚拟ULA 位置集合,然而,当阵元位置误差存在时,集合不存在重复位置差。 因此,针对阵元位置误差,提出了一种虚拟阵列提取方法,定义虚拟阵列的阵元位置集合C′为:

式中,Δm=min,min{·}表示集合“·”中的最小值。

此时,虚拟阵列的接收数据可表示为:

式中,A′=[a′(θ0)a′(θ1) …a′(θK-1)] 是阵元位置集合C′对应的阵列流型矩阵,其中a′(θk)=为第k +1 个信号的导向矢量;C′q表示集合C′中第q +1 个元素;I′C为中心元素为1、其余元素为0 的(2Lmax+1)×1 维列向量。

2.3 基于AMS-ANM 的DOA 估计方法

采用Jacobi-Anger 展开公式将阵列流型中的位置误差信息和角度信息进行分离,从而提取阵列流形A′的范德蒙德结构,构建原子范数最小化问题求解角度参数。

根据Jacobi-Anger 展开公式:

式中,Jh(r) 是以r为自变量的h阶第1 类贝塞尔函数。

由此,可将a′(θk) 中的第q +1 个数据展开:

根据第1 类贝塞尔函数的性质可得,随着阶数h的增加,Jh(r) 的值迅速衰减为0。 假设其最大阶数为正整数H,并且最大阶数的引入所带来的模型误差忽略不计。

由式(16)可推出虚拟阵列流型A′为:

式中,

则式(14)可转化为:

定义矩阵形式的原子集合为:

式中,A k代表集合A中的一个原子。 因此,可以定义矩阵Z在集合A上的原子范数为:

式中, inf ·{ } 表示集合“·”的下确界。

因此,将阵元位置误差下的嵌套阵列的DOA 估计问题可表示为如下的原子范数最小化问题:

式中,γ为平衡拟合误差和原子范数的正则化参数。

式(24)所示模型可转换为如下半定规划问题:

式中,T(u) 是由向量u =[u0,u1,…,u2H] ∈2H+1构成的Toeplitz 矩阵。 根据文献[19],式(25)所示的半定规划问题,可以由CVX 工具箱求解得到T(u) ,结合root-music 方法[20]求得θ的估计值。

综上,阵元位置误差条件下的嵌套阵列DOA 估计方法具体步骤如下。

输入: θs , R~s , PNA , R~ , H , I′C , γ ;步骤1:根据式(9)和式(10)得到P^NA ;步骤2:根据式(11)得到 Z~co ;步骤3:根据式(13)和式(14)得到C′和Z′;步骤4:根据式(18)构造矩阵V;步骤5:利用CVX 工具箱求解式(25)得到T(u);步骤6:结合root-music 方法实现DOA 估计;

3 仿真实验与结果分析

对所提AMS-ANM 方法进行性能仿真及性能分析。 阵列结构为二级嵌套阵,其中子阵1 和子阵2的阵元数均为4,假设第一个阵元为参考阵元。 仿真实验中分辨概率和均方根误差(Root Mean Squared Error,RMSE)运行结果均由200 次独立的蒙特卡罗实验统计获得,如无特殊说明,在每次蒙特卡罗实验中,给阵元位置添加[-0.1λ,0.1λ]的随机误差,将正则化参数设置为0.15。

3.1 阵元位置估计结果

设置单辅助校正源从θs =50°方向入射,信噪比为30 dB,快拍数为500,假设阵列所在平面为x-y平面,各阵元仅在x轴方向上存在位置误差,设置各阵元位置误差分别为0,-0.105λ,-0.085λ,0.04λ,0.025λ,-0.08λ,0.055λ,-0.065λ。 对阵元位置的估计结果如图2 所示。

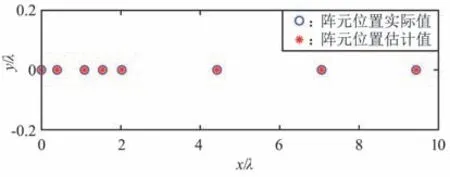
图2 阵元位置估计结果Fig.2 Estimation results of array element position

由图2 可知,在辅助信源精确无偏条件下,本文方法估计的阵元位置与实际阵元位置相一致。

3.2 Bessel 函数的最高阶数的选取

假设12 个窄带信号源均匀分布在 [40°,120°] ,信噪比为10 dB,快拍数为1 000,设置阵元位置的随机误差为[-0.15λ,0.15λ] 。 角度估计均方误差和运行时间随最阶数H的变化关系如图3所示。

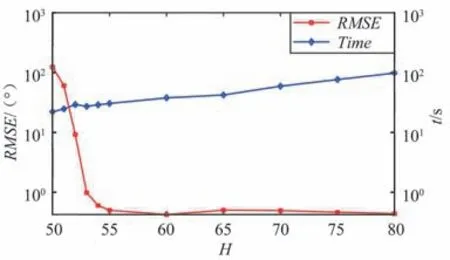
图3 RMSE 和运行时间随最高阶数的变化Fig.3 RMSE and running time versus highest order

由图3 可知,随着最高阶数H的增大,本文所提方法的角度估计精度提高,但最高阶数超过55 后,增大最高阶数H并不能提高所提方法的估计精度,H的增加反而会导致运算量的负担。 因此,本文在后续仿真实验中,将最高阶数设置为55。

3.3 分辨概率的比较结果

为了验证AMS-ANM 方法对相近的2 个信源的区分和估计能力,在不同信噪比和角度间隔下,仿真对比L1-SVD 方法[17]和矩阵重构[18]方法。 分辨概率随着信噪比和角度间隔的变化曲线如图4 和图5所示。 图4 中,设置θ1=40°,θ2=44°,快拍数为512,将信噪比从-5 dB 变化到20 dB。 图5 中,固定θ1=40°,θ2与θ1的间隔变化范围1°~7°,信噪比为15 dB。 如果和都小于,则认为2 个角度被成功分辨。

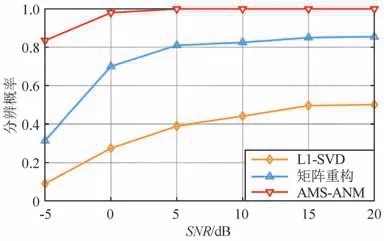
图4 分辨概率随信噪比的变化Fig.4 Resolution probability versus SNR

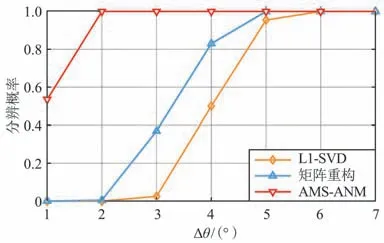
图5 分辨概率随角度间隔的变化Fig.5 Resolution probability versus angular interval

由图4 和图5 可知,在固定角度间隔为4°的情况下,由于基不匹配问题,L1-SVD 方法空间分辨率较低,矩阵重构方法未完全消除阵元位置误差的影响导致其分辨率不高,而AMS-ANM 方法通过阵列流型分离技术避免了阵元位置误差的影响,总体上优于对比算法。 在信噪比为15 dB 和快拍数为512的情况下,对比方法无法分辨相距较小的信源,而AMS-ANM 方法在角度间隔为2°时,分辨率可达100%。 因而本文方法在不同信噪比和角度间隔下均具有明显的空间分辨优势。

3.4 RMSE 随信噪比和快拍数变化的比较结果

DOA 估计的均方误差随快拍数和信噪比的变化关系分别如图6 和图7 所示。

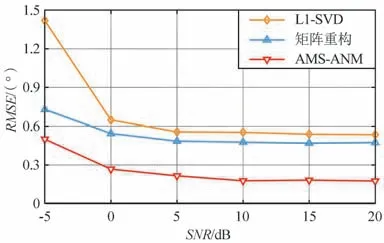
图6 估计精度随信噪比的变化Fig.6 RMSE versus SNR

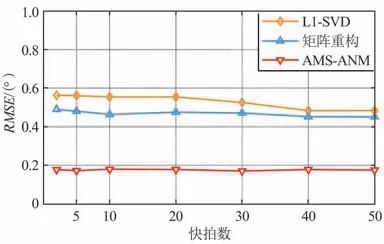
图7 估计精度随快拍数的变化Fig.7 RMSE versus snapshot number

图6 中,设置2 个信源的入射角分别为40°和75°,快拍数设置为512,信噪比从-5 dB 变化到20 dB。 图7 中,设置2 个信源的入射角分别为40°和60°,信噪比设置为15 dB,快拍数从2 变化到50。

由图6 和图7 可知,相比于其他方法,本文所提方法估计性能优良,即使在快拍数和信噪比较低的情况下具有良好的估计性能。

3.5 RMSE 随阵元位置误差变化的比较结果

下面验证阵元位置误差情况下的AMS-ANM 方法的估计性能,图8 表示DOA 估计RMSE 随阵元位置误差变化的关系。 实验中,设置10 个窄带信源号均匀分布在[40°,120°] ,快拍数为512,信噪比为15 dB,给阵元位置添加[-αλ/2,αλ/2]的随机误差,将α从0 变化到0.35。

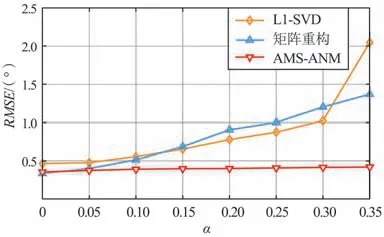
图8 估计精度随阵元位置误差的变化Fig.8 RMSE versus element position errors

由图8 可知,在欠定DOA 估计条件下,随着阵元位置误差增大,L1-SVD 和矩阵重构方法的性能恶化严重。 该实验结果表明,本文所提AMS-ANM 方法在不同阵元位置误差下具有鲁棒性。 同时,该实验证明了本文方法可实现欠定信号估计。

4 结束语

针对嵌套阵列DOA 估计方法在阵元位置误差条件下性能下降的问题,提出了一种基于阵列流型分离的最小原子范数DOA 估计方法,通过引入阵列流型分离技术有效消除阵元位置误差对嵌套阵列的影响。 仿真实验表明,相比于现有方法,本文所提方法具有更高的角度分辨率和估计精度,在不同阵元位置误差情况下,本文算法具有良好的鲁棒性,能够实现欠定DOA 精确估计。 然而,所提方法的运算量较大,如何降低运算量还需要进一步的研究。