基于芯样车辙试验的沥青混合料蠕变参数

张争奇,芮照诚,2,赵勤胜,李乃强,李宏伟

(1.长安大学 特殊地区公路工程教育部重点实验室, 陕西 西安 710064; 2.山东省交通科学研究院, 山东 济南 250102;3.山东省交通规划设计院集团有限公司, 山东 济南 250101; 4.唐山高速公路集团有限公司, 河北 唐山 063000)

1 前 言

时间硬化蠕变模型是表征沥青混合料蠕变规律的模型之一,在ABAQUS中该模型常被用于沥青路面车辙变形预估[1-4]。时间硬化蠕变模型参数对于预估的准确性具有重要影响,目前该参数一般通过单轴静载蠕变试验获取变形曲线,采用时间硬化蠕变模型进行拟合,进而得到表征沥青混合料变形特性的蠕变参数[5-6]。然而,该试验所采用的试件并非路面现场取样的试件,而是在实验室内成型获得,这样得到的蠕变参数并未考虑施工过程中各种因素对沥青路面质量的影响,难以准确地预估沥青路面车辙变形。

路面芯样是代表路面性能的有效单元,可以全面反映路面结构设计和施工质量。因此,利用路面芯样获取表征路面材料变形特性的蠕变参数对准确预测车辙变形具有重要意义。车辙试验仪是一种实验室常备试验设备,用来评价沥青混合料的高温抗变形能力。通过分析车辙试验中试件的受力特点和变形曲线特征发现,车辙试验可近似视为混合料的一种蠕变过程[7-10],且该试验方法更能体现沥青混合料车辙变形机理。方昊[11]通过时间硬化蠕变模型拟合室内车辙试验结果,得到了沥青混合料不同温度下的蠕变参数。因此,为获取能够反映沥青路面材料黏弹性的蠕变参数,本研究提出采用芯样车辙试验代替单轴静载蠕变试验确定模型参数,研究分析其可行性与合理性。

借助时间硬化蠕变模型分别对沥青混合料单轴静载蠕变试验结果、车辙试验结果以及路面芯样车辙试验结果进行拟合,得到不同试验条件下的路面材料蠕变参数并进行相关性分析,并验证材料蠕变参数的合理性。

2 实 验

2.1 原材料

选用SBS-1改性沥青、SBS-2改性沥青和SK-70基质沥青,粗、细集料均采用石灰岩,矿粉采用石灰岩粉。经检验,上述试验材料均满足相关规范要求。选用三种常用级配类型AC-13、AC-20和AC-25,其组成见表1。

表1 沥青混合料级配组成

采用Superpave体积设计法确定最佳油石比,分别为4.9%、4.3%和3.9%。

2.2 实验方法

对制备的沥青混合料试件和路面芯样分别进行单轴静载蠕变试验和车辙试验。

2.2.1单轴静载蠕变试验 采用Troxler4140型旋转压实仪成型尺寸为φ150 mm×170 mm的圆柱形试件,钻芯得到尺寸为φ100 mm×150 mm的试件(图1)。采用UTM-30型万能材料机进行单轴静载蠕变试验,试验温度为30～70 ℃。

图1 单轴静载蠕变试验试件

2.2.2车辙试验 采用沥青混合料圆柱形试件和路面芯样进行车辙试验[12-13],设计了圆柱形试件车辙试验模具(图2),将成型圆柱形试件或路面芯样按照尺寸切割并放置于车辙试验模具中进行试验。

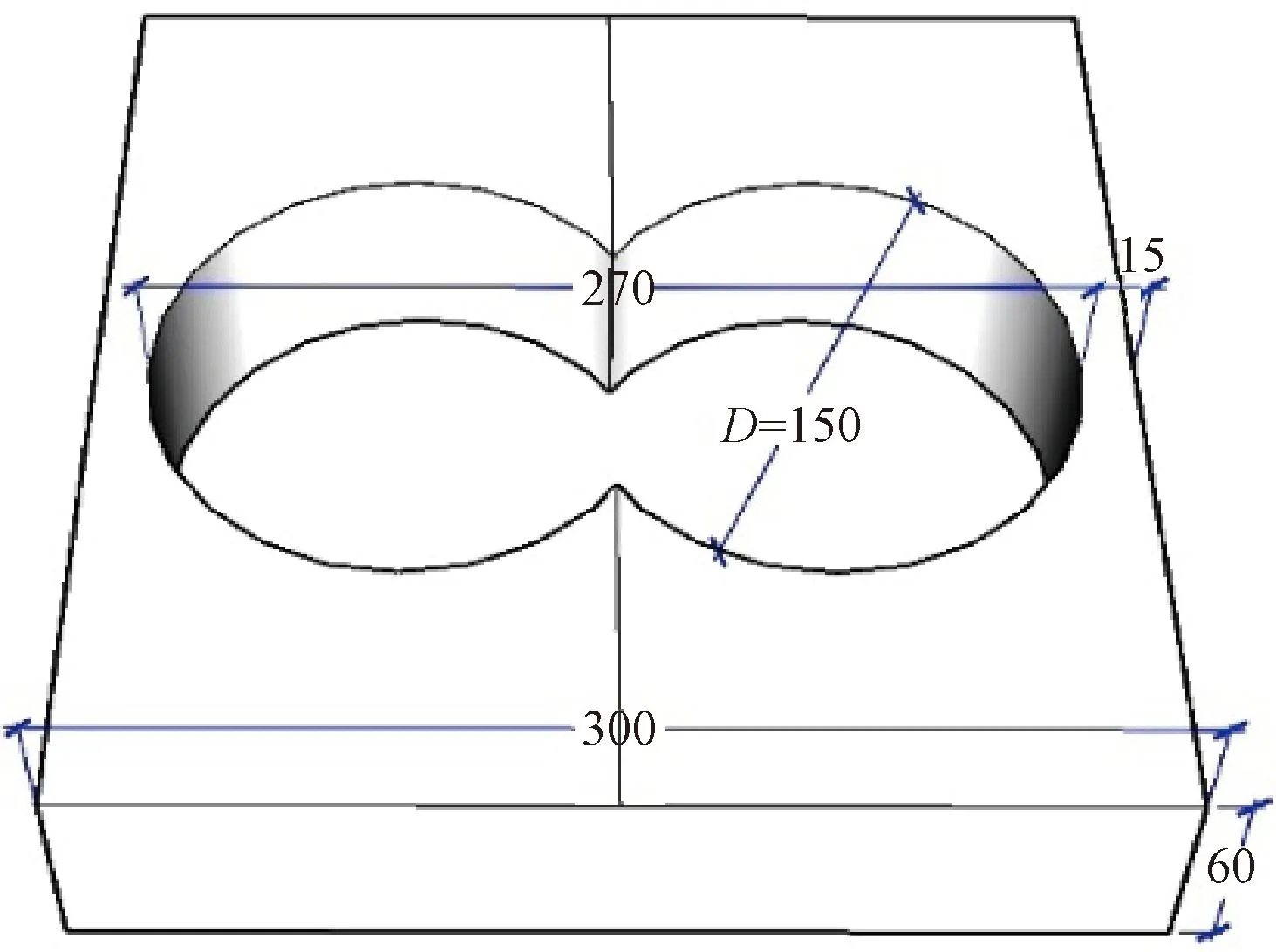
图2 圆柱形试件车辙试验模具(单位：mm)

具体试验方案如下：将旋转压实仪成型的沥青混合料试件或路面芯样,按照模具尺寸进行切割(见图3);根据试件厚度选择合适的垫片,将切割后的试件和垫片放入模具(见图4);将车辙试件置于试验仪进行试验;试验轮压强为0.7 MPa,试验温度与单轴静载蠕变试验相同。

图3 切割后的圆柱形试件

图4 由切割后的圆柱形试件与模具组合而成的车辙试件

3 基于单轴静载蠕变试验的沥青混合料蠕变参数

3.1 时间硬化蠕变模型

为探究沥青路面材料的蠕变特性,采用Bailey-Norton蠕变规律对沥青混合料及路面芯样的变形进x行分析,时间硬化蠕变模型可表示为：

εcr=C1qC2tC3

(1)

式中：εcr为蠕变量;q为应力;t为时间;C1、C2、C3为模型参数,一般C2≥0,C3≤1。

当应力不变时,对时间求导可得蠕变变化率的表达式：

(2)

令：A=C1C3,幂法则乘数;m=C2,等阶应力阶次;n=C3-1,时间阶次。

则有：

(3)

3.2 室内圆柱形试件单轴静载蠕变试验

在30～70 ℃(10 ℃为一个间隔)条件下,对所成型的圆柱形试件进行单轴静载蠕变试验,得到不同温度下混合料的蠕变变形随时间的变化规律。在处理蠕变试验数据时需将应变对数化处理,得到三种沥青混合料在不同温度下的应变,如图5所示。

图5 沥青混合料单轴静载蠕变试验结果 (a)AC-13;(b)AC-20;(c)AC-25

从图5可知,沥青混合料的蠕变变形随时间逐渐增大;在同一时间,变形随温度增大而增大;AC-25的蠕变变形最大,AC-13和AC-20变形相差较小。三种沥青混合料蠕变发展趋势基本相同,在应力加载的初始阶段,混合料的变形发展迅速,在300 s左右时,试件的变形增长趋势减缓,从500 s左右开始,沥青混合料的蠕变变形大致呈现稳定发展趋势。

借助式(1)对上述试验结果进行拟合,发现得到的蠕变参数变异性较大,这是因为参数C1、C2、C3并非相互独立,而是存在一定相关性。为解决这一问题,根据文献[14-15],固定C2=0.65即m=0.65,拟合结果与试验实测数据相关性较高,相关系数均在0.95以上。相关蠕变参数如表2所示。

表2 沥青混合料单轴静载蠕变试验的时间硬化蠕变模型参数

由表2可知,沥青混合料的蠕变参数幂法则乘数(A)和时间阶次(n)均随温度呈增大趋势。三种级配沥青混合料中,A在60 ℃及以下时,大小及变化趋势几乎一致,在70 ℃时相差较大;n随温度变化逐渐增大,其中AC-25最大,AC-13最小。

4 基于圆柱形试件和路面芯样车辙试验的蠕变参数

4.1 室内圆柱形试件车辙试验

车辙试验变形量累积过程可反映沥青混合料在荷载作用下的黏弹变形发展趋势。采用车辙试验仪对圆柱形试件进行车辙试验,得到的蠕变曲线见图6。

图6 沥青混合料的车辙试验结果 (a)AC-13;(b)AC-20;(c)AC-25

由图6可知,沥青混合料车辙试验变形量随时间大致呈幂函数增长趋势,与单轴静载蠕变试验结果相似性较高,因此,利用时间硬化蠕变模型拟合车辙试验结果具有可行性。车辙试验所得试验数据是变形量随时间的变化,而式(1)表征的是应变随时间的变化规律,故需对车辙试验数据进行处理,将试件变形量转化为应变进行拟合。拟合得到的蠕变参数见表3。

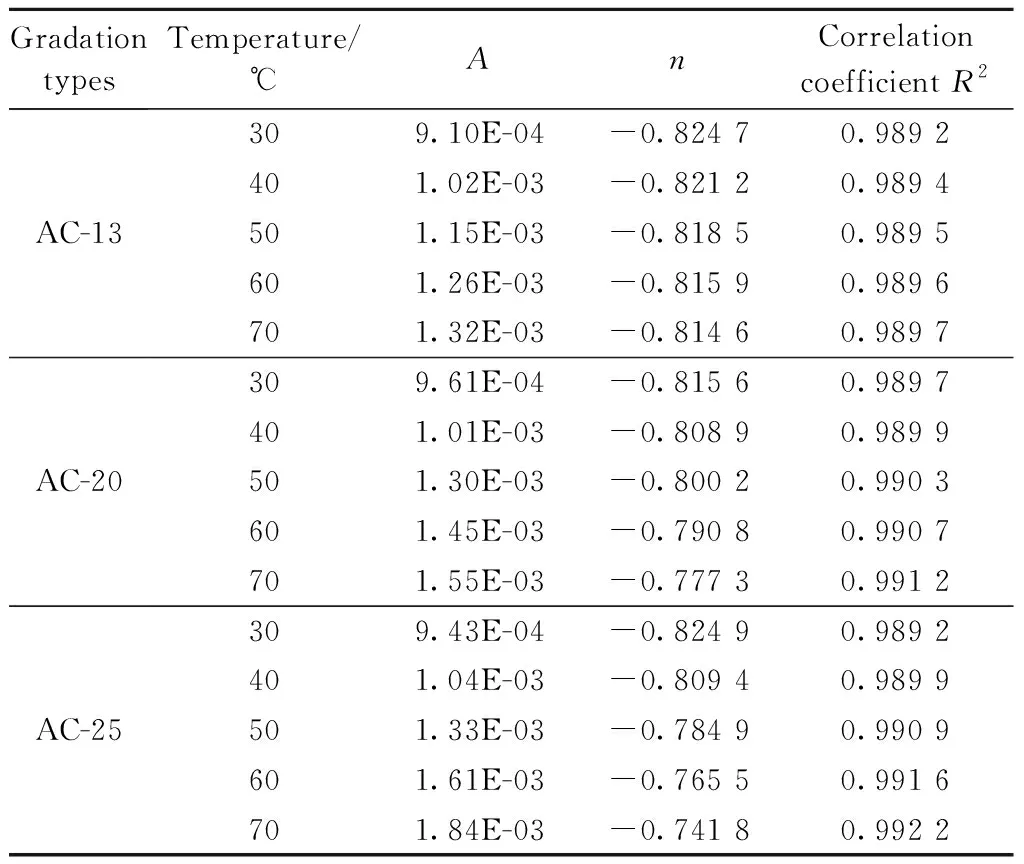
表3 沥青混合料车辙试验的时间硬化蠕变模型参数

由表3可知,室内圆柱形试件车辙试验的A随温度增加呈线性增长趋势,在30和40 ℃条件下,三种沥青混合料相差不大,在50 ℃及以上时,AC-25最大,AC-20和AC-13次之;n随温度也呈线性增长趋势,其中,AC-13随温度变化增长不明显,AC-20和AC-25随温度增长较快。

4.2 路面芯样车辙试验

基于室内圆柱形试件车辙试验结果,得到了时间硬化蠕变模型参数,但这并不能够代表沥青路面材料的变形特性。因为在沥青路面的实际建设过程中会受到各种因素的影响,即使是同样设计的沥青混合料,建成后路面的变形特性与室内成型的试件相比仍存在较大的差异,而现场钻取的芯样更能反映沥青路面混合料的实际性能。在施工现场取样进行芯样车辙试验,进一步验证车辙试验获取蠕变参数的合理性,同时也对室内车辙试验的时间硬化蠕变模型参数进行修正。芯样车辙试验结果见图7。

图7 路面芯样车辙试验结果 (a)AC-13;(b)AC-20;(c)AC-25

通过钻取路面芯样,经切割获取芯样车辙试验试件,对芯样试件进行不同温度条件下的车辙试验,并利用时间硬化蠕变模型进行参数拟合。在拟合过程中发现芯样车辙试验结果稳定阶段的应变变化速率与室内圆柱形试件十分接近,故n与圆柱形试件车辙试验拟合结果保持一致,根据芯样车辙试验结果确定A,拟合得到的蠕变参数见表4。

表4 路面芯样车辙试验的时间硬化蠕变模型参数

由表4可知,与圆柱形试件车辙试验结果拟合数据相比,A值偏大,这是因为路面施工现场因素众多,条件复杂,很难达到实验室所制备的试件质量,导致路面芯样的抗变形能力稍弱。

5 蠕变参数相关性分析

两种车辙试验条件下的时间硬化蠕变模型参数幂法则乘数(A)之间的相关性如图8所示,换算公式见表5。

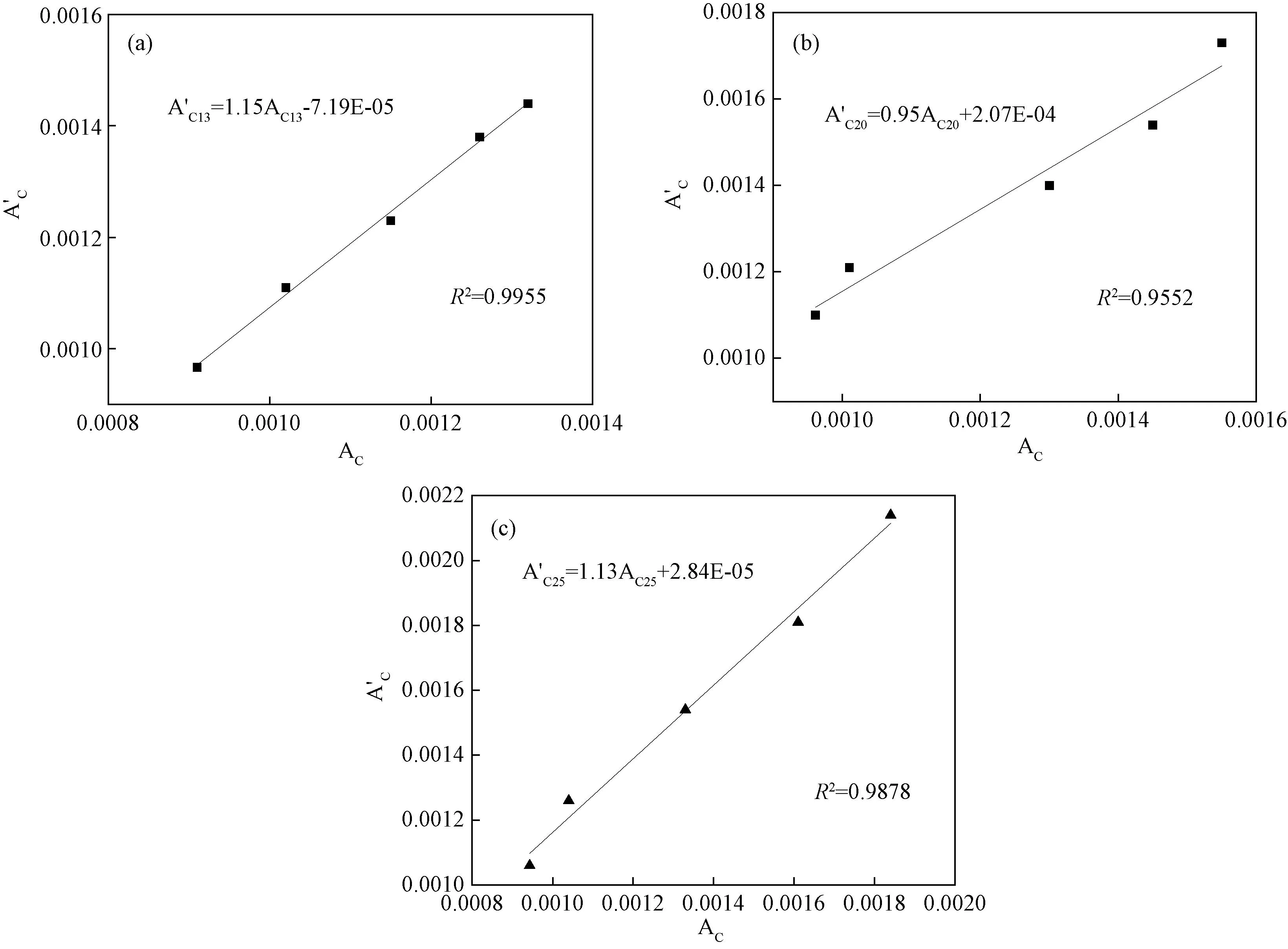
图8 路面芯样与沥青混合料车辙试验的参数(A)相关性分析 (a)AC-13;(b)AC-20;(c)AC-25

表5 路面芯样与沥青混合料车辙试验参数(A)换算公式

同理,根据单轴静载蠕变试验结果和芯样车辙试验结果,可以得到两者蠕变参数之间的相关关系,换算公式见表6。

表6 路面芯样与沥青混合料的蠕变参数(A)和(n)换算公式

由表6可知,基于单轴静载蠕变试验的沥青混合料试件蠕变参数与基于路面芯样修正后的蠕变参数之间具有良好的相关性,可以建立可靠的换算公式,前者是基于室内成型的试件得出,可以代表沥青混合料的变形特性,后者则代表沥青路面验收阶段的变形特性,两者之间良好的换算关系证明采用芯样车辙试验代替单轴静载蠕变试验获取蠕变参数是可行的。因此,在沥青路面验收阶段,可以通过钻取路面芯样进行车辙试验,获取表征沥青路面材料变形特性的蠕变参数,进而采用有限元法对车辙进行预估,以评价沥青路面的抗车辙能力。

6 结 论

圆柱形试件车辙试验结果与芯样车辙试验结果相似性高,采用时间硬化蠕变模型对两条试验曲线进行拟合得到的幂法则乘数(A)之间存在线性换算关系,这说明芯样试件可以表征路面材料的变形特性。

基于单轴静载蠕变试验结果拟合得到的蠕变参数与基于路面芯样车辙试验结果修正得到的蠕变参数之间具有良好的相关性,说明采用路面芯样车辙试验获得的时间硬化蠕变模型参数具有可行性及合理性,可用于有限元法沥青路面车辙预估模型,评价其抗车辙能力。