基于GP14.3运动学混合震源模型和SPECFEM 3D谱元法的宽频地震动模拟

巴振宁， 赵靖轩， 张郁山， 梁建文， 张玉洁

1 天津大学中国地震局地震工程综合模拟与城乡抗震韧性重点实验室， 天津 300350 2 天津大学土木工程系， 天津 300350 3 中国地震灾害防御中心， 北京 100029

0 引言

近年来，近场强地面运动模拟逐渐成为工程地震学和理论地震学的一个热点课题，相关研究可为强震记录不足地区的工程结构抗震设防以及城市防震减灾提供依据(王海云和谢礼立, 2008).随着城市现代化的发展，超高层建筑、长大桥梁、超高拱坝等一些重大工程结构不断涌现，对这些具有较长自振周期的工程结构进行抗震分析时，需要考虑低频地震动(<1 Hz)对结构非线性响应产生的重要影响，尤其是近断层区可能存在的长周期速度大脉冲；而高频地震动(>1 Hz)控制着地震动的幅值，对结构地震反应同样也不可忽视(许可, 2020).因此，开展宽频带地震动模拟研究以为工程结构抗震设防提供合理输入有着重要的科学意义和工程应用价值.

目前宽频地震模拟的主流方法是将确定性方法模拟的低频地震动和随机方法模拟的高频地震动相结合的混合方法(Graves and Pitarka, 2010; Frankel, 2009; Mai et al., 2010; 孙晓丹和陶夏新, 2012).但该方法无法反映三维地形对高频地震动产生的影响(Lin et al., 2011; Baltay et al., 2017; Sahakian et al., 2019).同时，随机方法得到的结果仅是一条方向未知的水平向加速度时程，而确定性方法能够获得三分量地震动，两者的叠加具有不协调之处(曹泽林, 2020).为避免上述问题，综合考虑震源-传播-场地整个物理机制对地震波场特性影响，采用完全确定性方法进行的宽频带地震动模拟逐渐成为一种趋势.

确定性的宽频地震动模拟依赖于高效的解析或数值方法以及合理的震源模型.目前，确定性的宽频地震动模拟可采用频率波数域(FK)和各种数值方法.其中，FK方法作为一种半解析方法，适用于水平成层的一维波速结构模型内源引起的响应问题，由于无需划分网格且自动满足无穷远波辐射条件，模拟精度高、模拟带宽范围较广(Cao et al., 2019; 梁建文等, 2022).确定性方法中有限元法(FEM)、有限差分法(FDM)、谱元法(SEM)等数值方法能够计算三维复杂场地的地震响应，但由于对区域地壳内小尺度不均匀体和震源的高频特征缺乏足够认识，导致了上述方法在过去多限于低频模拟.但由于地震和背景噪声记录的不断丰富，相关学者通过反演等手段对地下波速结构有了更加清晰的认识.同时，已有学者提出了能够激发宽频地震波的合理运动学或动力学震源模型.针对运动学震源模型，目前主要包括确定性震源、随机震源和混合震源模型(王海云等, 2008)：确定性震源模型主要强调了断层面上凹凸体对震源破裂的控制作用(Irikura and Miyake, 2011)；随机震源模型主要强调震源产生的随机散射和介质不均匀导致的高频扰动作用；混合震源模型由于同时考虑了破裂面上凹凸体对滑动量不均匀分布的主导作用和滑动量的随机性，是激发宽频地震波的合理震源模型.

目前，随着相关学者针对地下波速结构和震源破裂的认识逐渐深刻，以及超级计算的出现突破了计算能力和计算耗时的瓶颈，推动了各数值方法在区域尺度宽频带地震动模拟方面的发展.基于数值方法的模拟区域范围从几十公里到几百公里，网格单元的总数从数百亿到数千亿；模拟的频率从2～5 Hz、10 Hz或更高，已基本可以覆盖工程结构敏感频段.事实上，美国劳伦斯国家重点实验室Rodgers等(2019, 2020)最新证实了0～5和0～10 Hz的宽频模拟可采用完全确定性物理的技术实现.Fu等(2017) 借助神威太湖之光超级计算机，针对1976年唐山大地震实现了整个华北地区的宽频(0～18 Hz)地震动模拟.上述成果表明，基于确定性的宽频带地震动模拟是现代地震工程地震动模拟的重要发展方向.

因此，本文为实现基于谱元法的确定性宽频地震动模拟，主要开展了两项工作.首先，将确定性凹凸体震源模型和Graves和Pitarka(2010, 2015)提出的GP14.3随机震源模型结合，进而给出了一种能激发宽频地震波的混合震源模型；将上述运动学混合震源模型开发到了SPECFEM 3D开源代码中，实现了基于GP14.3混合运动学震源模型和SEM的全过程宽频带地震动模拟.

1 谱元法及混合运动学震源模型

1.1 SEM理论

SEM属于广义有限元法，建立在波动方程的弱形式理论基础上，是求解偏微分方程的一种有效的数值计算方法.该方法集整了伪谱法和FEM的优势，兼备了伪谱法的高精度、快速收敛和FEM高灵活性的特点.并且SEM划分的单元更稀疏，可避免高阶有限元可能存在的Runge现象.此外，由于单元质量阵为对角阵，因此大大减少了计算存储，易于在多节点上实现并行计算(李孝波等, 2014).近年来，随着Komatitsch和Tromp(1999)将SEM推广到地震波场的模拟并推出适用于二维和三维问题的谱元程序SPECFEM 2D及SPECFEM 3D，SEM作为一种高精度的数值方法得到越来越广泛的应用.在本节中简要介绍SEM(基于Legendre展开)的求解过程.

震源激发的地震波满足线弹性动力学控制方程：

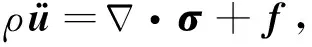
(1)

σ=c∶ε,

(2)

式中，c为介质刚度张量，“∶”为张量乘法，ε为应变张量，其表达式为

(3)

震源项f为一双力偶点源，一般可以表示为

(4)

式中，M为对称矩张量，其各元素表示描述震源错动中的经分解后的不同位态.S(t)为描述震源破裂过程的震源时间函数，x和xS为任一场点和震源位置处.由于在宽频地震动受震源破裂过程的影响，使用单个点源描述发震机制不再符合实际情况，故需要将破裂过程等效为多个子源叠加，包括各个子源的矩张量和时间函数，描述混合震源模型破裂过程的时空分布.

将式(2)—(4)代入式(1)中，结合自由表面零应力条件可得到计算域Ω的弱形式：

(5)

式中，w为引入的任意试函数，以此模型表面零应力条件已自动满足，这也是采用方程弱形式区别于强形式的最明显特征.另一方面，采用nl阶六面体对三维计算域进行离散，进而某特定谱单元Ωe上的函数可用其上的GLL插值节点表征：

(6)

式中，fα β γ为参考点处的插值形函数权值，lk(k=α,β,γ)为k阶Lagrange多项式，(ξ,η,ζ)为离散六面体单元对应的标准参考单元上的插值节点，它与六面体上的插值点x=(x,y,z)建立了一一映射的关系，且有

dxdydz=Jedξdηdζ,

(7)

式中，Je表示Ωe与其对应参考单元的三阶Jacobian矩阵.因此式(5)中函数在谱单元上的积分可利用GLL积分法则简化为

(8)

式中，ωk(k=α,β,γ)为GLL点上的积分权值.进一步通过方程集整，叠加邻接谱单元对共享节点的贡献，可建立起关于整体位移向量U的常微分方程：

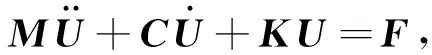
(9)

式中，M、C和K分别为对角质量矩阵、吸收边界矩阵和刚度矩阵.上述方程可采用显式Newmark-β法高效求解：

(10)

SEM模拟波动传播时涉及相对周期误差(物理频散)和数值阻尼误差，前者是对波传播过程中由于网格尺寸、积分方法和单元类型的改变导致对波速的错误估计造成.采用CFL(Courant-Friedrichs-Lewy)条件对显式格式中的步长施加约束：Δt≤γΔxmin/vmax，其中γ为严格小于1的常数，Δxmin和vmax为模型GLL节点间最小距离和最大波速，同时网格划分尺寸应满足条件：s≤λminN/5，其中λmin为介质中传播最短波长，N为Lagrange多项式的阶数，取4≤N≤8，一般取N=4.

1.2 基于GP14.3的混合震源在SEM中的开发

混合震源模型主要是将低波数确定性的凹凸体震源模型中引入高频随机成分，以确保合成宽频地面运动的带宽有效性.首先根据定标率建立包含凹凸体震源的有限断层模型，确定性的凹凸体震源建立过程不再过多阐述，具体细节可以参考王海云(2004).进而在凹凸体震源分布的基础上考虑在断层面滑动分布中结合Graves和Pitarka(2010, 2015)提出的GP14.3随机震源模型，该随机震源模型采用半随机方法，即调整随机错动分布使其具有k-2波数谱，是一种经过多位学者验证过，并且成功应用到旧金山地区海沃德断层的宽频带强地面模拟中较为成熟的随机震源模型.本节将主要介绍GP14.3随机震源公式的推导以及将混合震源开发到谱元程序SPECFEM 3D中的流程.

首先将已有的凹凸体断层面上滑动量的空间分布经二维傅里叶变换至波数域，得到断层面上确定性的滑动波数谱Dslip(ks,kd):

Dslip(ks,kd)=∬Uslip(x′,y′)e-iksxe-ikdydksdkd,

(11)

式中，ks、kd分别表示沿断层面走向、倾向的波数，Uslip(x′,y′)表示断层面上滑动量的空间分布，坐标(x′,y′)位于断层面上的局部坐标系中.

其次采用波数衰减满足von Karman自相关函数的波数谱并引入随机数φ表达震源中的随机成分(Mai and Beroza, 2002)：

(12)

式中，φ是(-π, π)区间上服从均匀分布的随机数，H是Hurst指数，这里根据Graves和Pitarka(2015)设置为0.75，as和ad设置为与震级MW相关的两个经验系数

(13)

然后在波数域中结合确定性的低波数谱和随机高波数谱，并利用二维逆傅里叶变换至空间域中：

×Dslip(0,0)(1-W)]eiksxeikdydksdkd,

(14)

式中，Dslip(0,0)表示走向、倾向为0时的滑动波数谱，W表示波数结合函数，用以选择确定性部分的低波数成分和随机部分的高波数成分，其表达式为

(15)

式中，N控制结合的锐度，设置为4；kcs和kcd表示沿断层走向和倾向的拐角波数，用以确定震源谱中低波数和高波数的结合界限，设置kcs=1/断层沿走向长度，kcd=1/断层沿倾向宽度.由此，断层面上的滑动量分布得以确定.

最后基于断层面上的滑动量可以得到每个断层上的M0，进而根据断层的走向、倾向和滑动角得到每个子源对应的地震矩张量.

关于破裂起始时刻的分布(即断层面上的破裂传播过程)，首先需要确定破裂速度的初始分布.考虑浅地壳层区域的破裂能力相较于深层弱(Kagawa et al., 2004)，将地表以下5 km深度范围内的平均破裂速度设置为剪切波速的56%，深度大于8 km处破裂速度设定为剪切波速的80%，5～8 km的区域设置为线性过渡区域，因此破裂速度沿深度范围的初始分布可以表示为

(16)

进而根据子源中心至破裂起始点的直线距离和初始破裂速度分布即可确定断层面上各子源的破裂起始时刻Tij0，而后考虑各子源滑动量对各自破裂起始时刻的时间扰动并引入随机数，得到破裂起始时刻的空间分布：

(17)

式中，M0表示总地震矩大小，sij表示各子源的滑动量，sA表示断层面上的平均滑动量，sM表示所有子源中最大滑动量，ε表示服从标准正态分布的随机数，σT是对数正态标准差，此处设置为0.2.

考虑浅层地壳(z<5 km)的破裂持时是较深处的(z>8 km)的2倍，其间为线性过度，各子源的上升时间可以表示为

(18)

最后根据断层面上的平均上升时间τA(公式(19))按比例调整各子源的上升时间，即可得其在断层面上的空间分布.

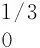
(19)

式中，c1为计算常量，取为1.45×10-9，αT为缩放系数，与断层的滑动角(λ)和倾角(δ)相关:

αT=[1+FDFRcα]-1,

(20)

(21)

(22)

FD和FR分别为倾角和滑动角因子，cα为针对逆断层的高频辐射因子.

此外，同样为了考虑各子源滑动量对各自上升时间的时间扰动通过引入随机数，得到各个子源上升时间的空间分布：

τi=τ0iexp(εσR)，

(23)

式中，τ0ij表示各个子源的初始上升时间，ε表示服从标准正态分布的随机数，σR是对数正态标准差，此处设置为0.5.

对于一个设定地震，基于SPECFEM 3D建立GP混合运动学震源模型的整个流程(图1)可以归纳为如下7个步骤：

图1 基于SPECFEM 3D混合运动学震源建模流程图Fig.1 Flow chart of hybrid kinematic source based on SPECFEM 3D

(1)借助全局参数定标律，估计破裂面的尺寸和平均滑动量.进一步将整个破裂面划分为NL×NM个矩形小网格.

(2)借助全局参数与局部参数间的定标律，估计最大凹凸体的尺寸和平均错动量，并将其定位在破裂面上，然后再根据整个破裂面上的平均错动量估计凹凸体外断层的错动量.

(3)借助二维傅里叶变换将上述确定性的错动分布转换得到确定性波数谱，借助式(12)引入的随机波数谱，将确定性的低波数谱和随机高波数谱结合，最后二维逆傅里叶变换至空间域中，得到各个网格的错动量.

(4)根据(3)计算得到的各个子源的错动量，计算得到每个子源的矩张量，并确定各个子源的位置，生成谱元程序SPECFEM 3D中的要震源参数文件CMTSOLUTION.

(5)根据断层埋深确定破裂速度和上升时间的初始分布，而后考虑各子源滑动量对各子源的破裂速度和上升时间的扰动并引入随机数因子，得到破裂速度和上升时间的时间分布.

(6)根据子源对应的破裂时间和上升时间，选定的震源函数形式以及时间步长的大小，得到每个子源对应的震源时间.

(7)由于每个子源时间函数不同，故需要从主参数文件Par_file中设置EXTERNAL_SOURCE_FILE为true，并且在震源参数文件CMTSOLUTION中每个子源中额外加入对应的时间函数文件的路径.

2 精度验证：一维波速结构地震动模拟

为验证SEM模拟宽频带地震动的精度，本节与基于修正动力刚度矩阵的FK方法(Ba et al., 2021, 2022)进行对照.前文提及的FK方法作为一种半解析方法，模拟精度高、模拟带宽范围较广，适合作为对比验证的参照结果.故本节分别基于SEM和FK方法在一维波速空间下针对同一混合震源模型进行模拟，比较两种方法模拟得到0～10 Hz的地震动时程和频谱曲线.

本文基于上述两种方法分别建立了均匀和多层的一维波速结构模型，两种模型大小均为60 km×60 km×40 km，速度结构参数分别见图2(a,b).本节与FK方法对比的模拟结果的频带范围为0～10 Hz，SEM中为保证计算结果的精确可靠，要求最短波长中至少包含5个GLL节点，需要根据模拟频率范围确定网格大小.模型采用Trelis软件进行划分，图2(a，b)分别为均匀和多层模型谱单元网格图，其中单层模型网格总数约为270万，GLL节点数量为1.94亿个；多层模型网格总数约为340万，GLL节点数量为2.54亿个.

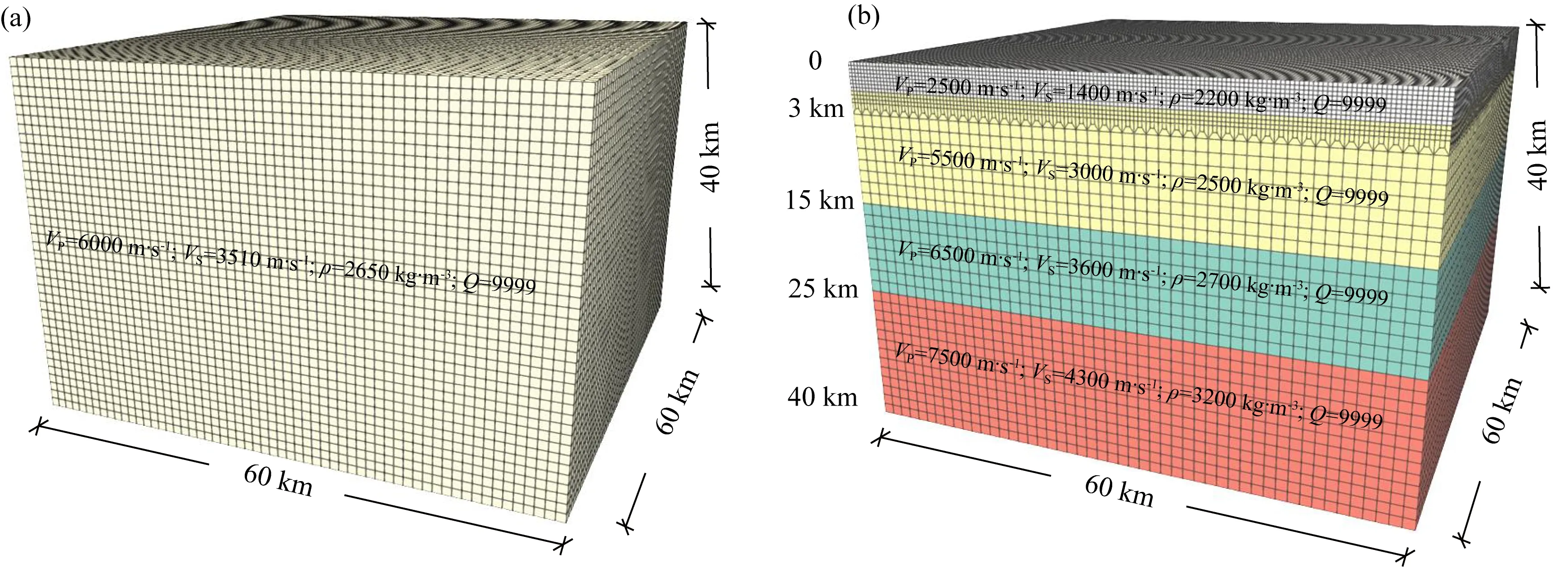
图2 均匀(a)和多层(b)一维波速结构模型图中VP为P波波速，VS为S波波速，ρ为密度，Q为品质因子.Fig.2 Homogeneous (a) and multi-layer (b) 1D wave velocity structure modelsVP is P-wave velocity, VS is S-wave velocity, ρ is density, Q is quality factor.

根据上述两种一维波速结构模型分别建立对应的混合震源模型.本文选择建立MW6.0走滑断层的混合震源模型，首先根据定标律确定断层的全局震源参数，见表1所示.

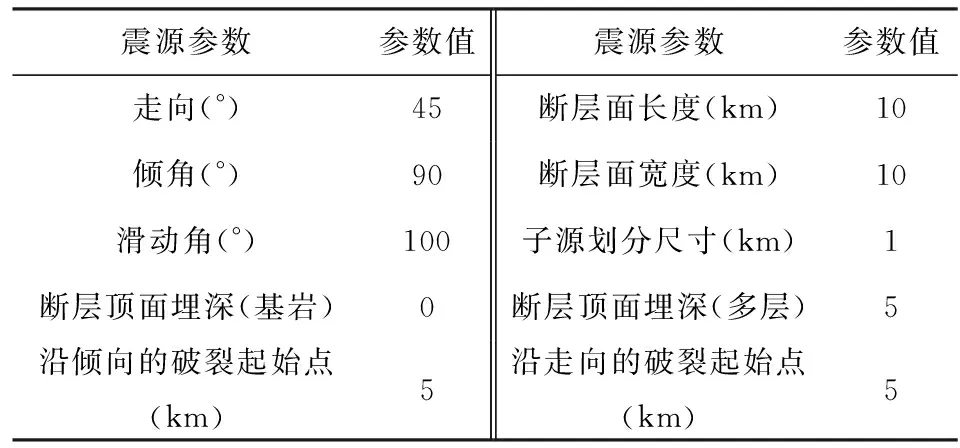
表1 断层全局震源参数Table 1 Fault global source parameters

考虑到本次地震震级小于6.5级，断层面上采用单凹凸体，根据姜伟等(2017)中走滑断层的定标率公式，计算得到震源的局部参数见表2所示.由于断层在均匀半空间和多层一维波速结构情况下的埋深不同，断层位置周围对应的波速不一致，根据1.2节中式(11)—(15)计算断层面滑动量分布，式(16)—(23)计算得到断层各个子源的破裂时间和上升时间，最终得到的均匀和多层一维波速结构模型的震源模型如图3所示.

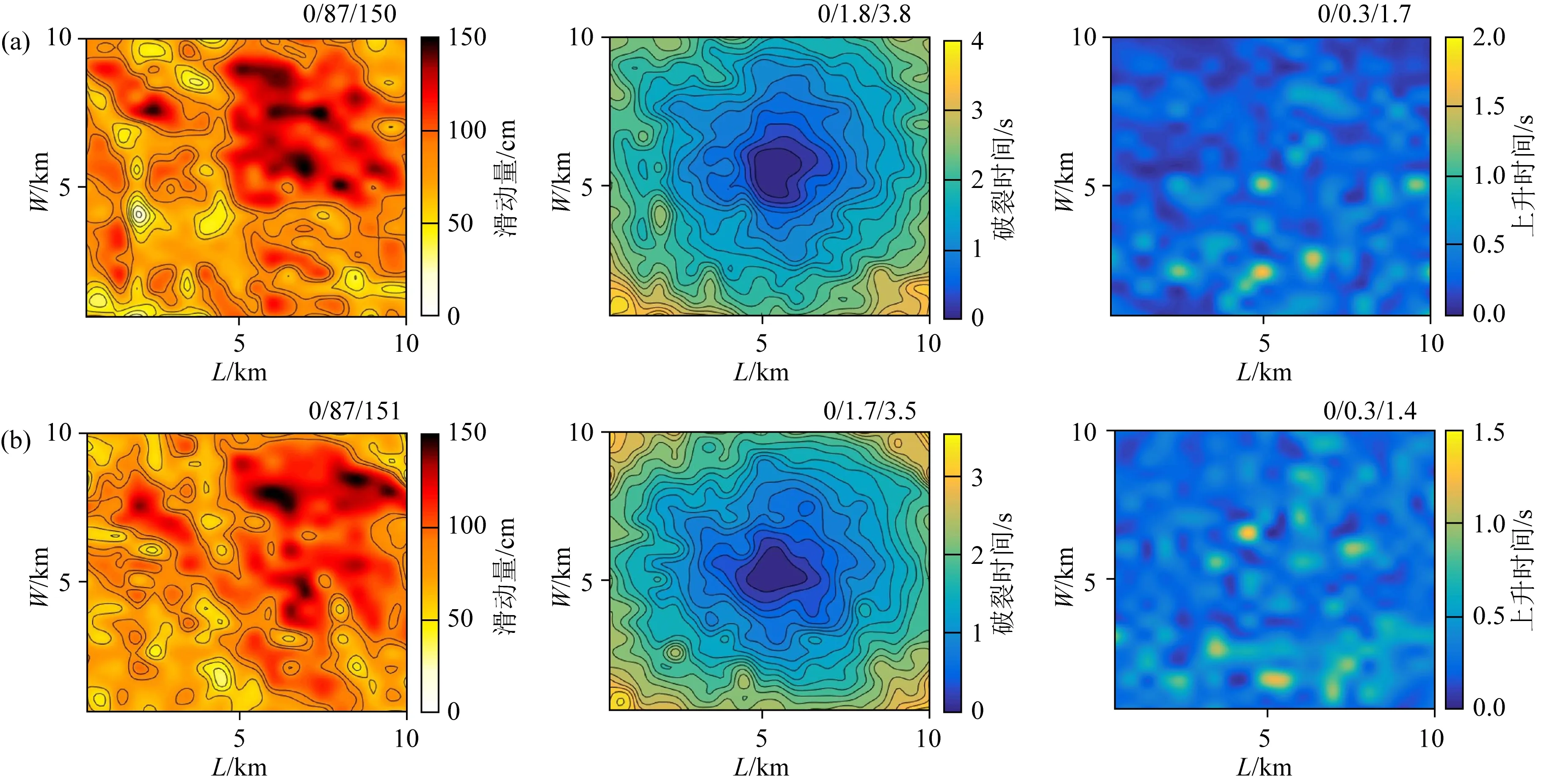
图3 均匀(a)和多层(b)一维波速结构模型对应的混合运动学震源每个子图右上角的数字三值组分别表示给定分布的最小值、平均值和最大值.Fig.3 Homogeneous (a) and muti-layer (b) hybrid kinematic source model Triplet of numbers at top right of each panel indicates the minimum, mean and maximum values of the given distribution, respectively.

表2 断层局部震源参数Table 2 Fault local source parameters

限于篇幅，仅给出了由表面处沿着断层方向和垂直断层方向震中距为10 km位置处(见图4)加速度三分量时程和对应的频谱结果.其中，图5为均匀一维波速结构模型结果，图6为多层一维波速结构模型结果.结果表明：基于SEM模拟的加速度时程波形、持时和幅值以及频谱结果在0～10 Hz的频率范围内与FK方法的结果一致，验证了基于GP混合运动学震源模型在SEM模拟的精度.

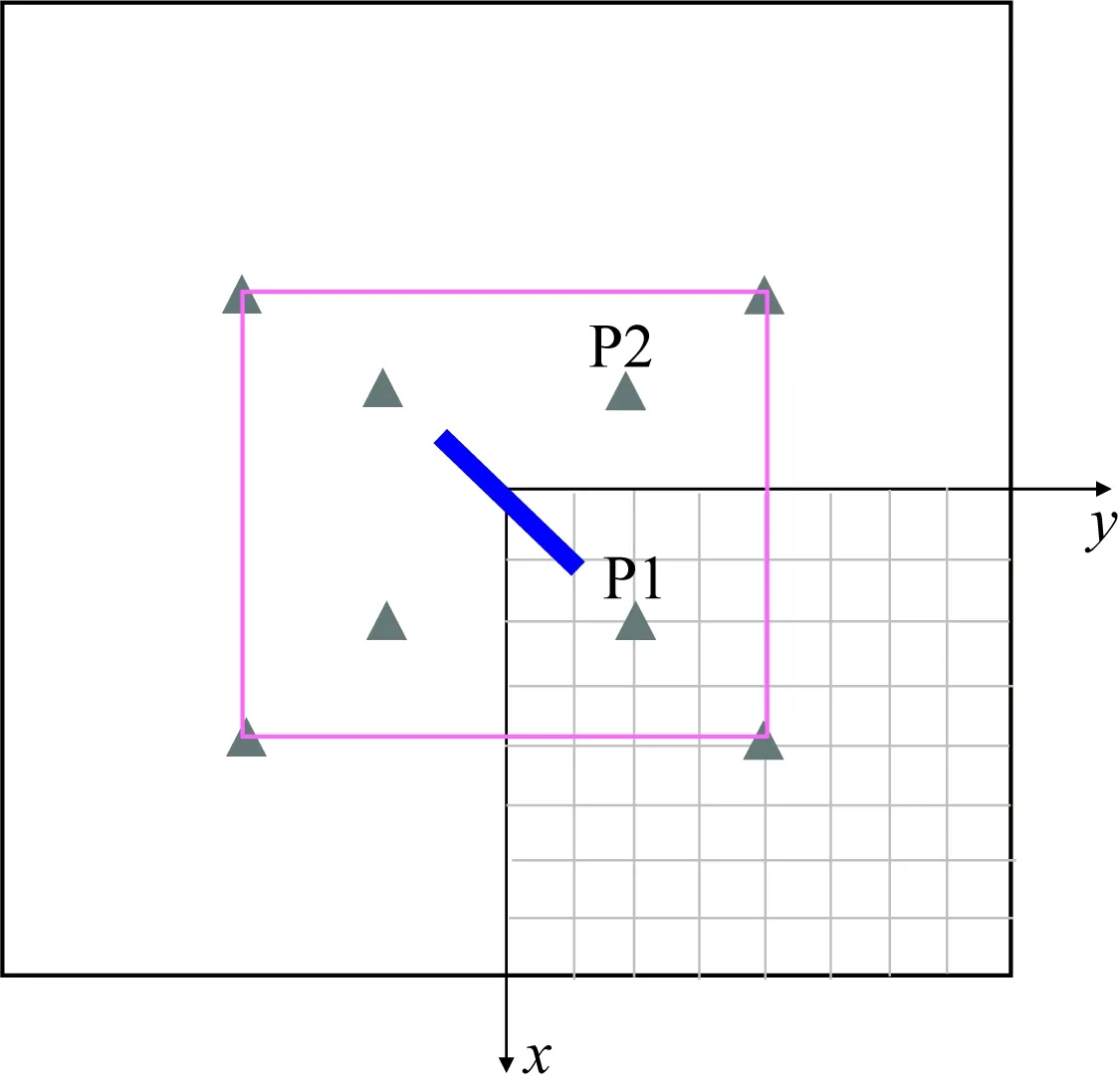
图4 观测点P1和P2位置Fig.4 Observation points P1 and P2

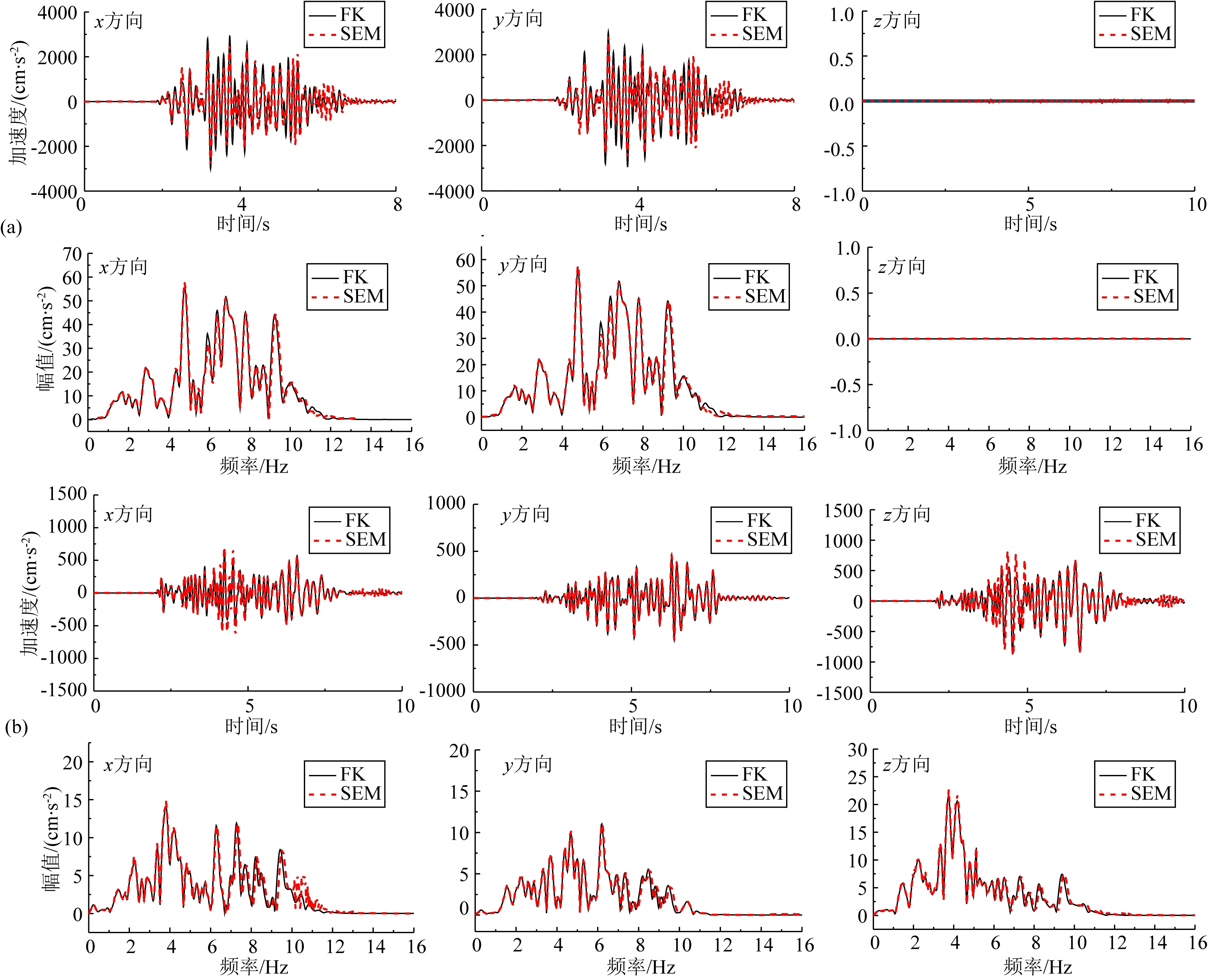
图5 P1(a)和P2(b)均匀一维波速结构模型计算结果Fig.5 Calculation results of P1 (a) and P2 (b) homogeneous 1D wave velocity structure models

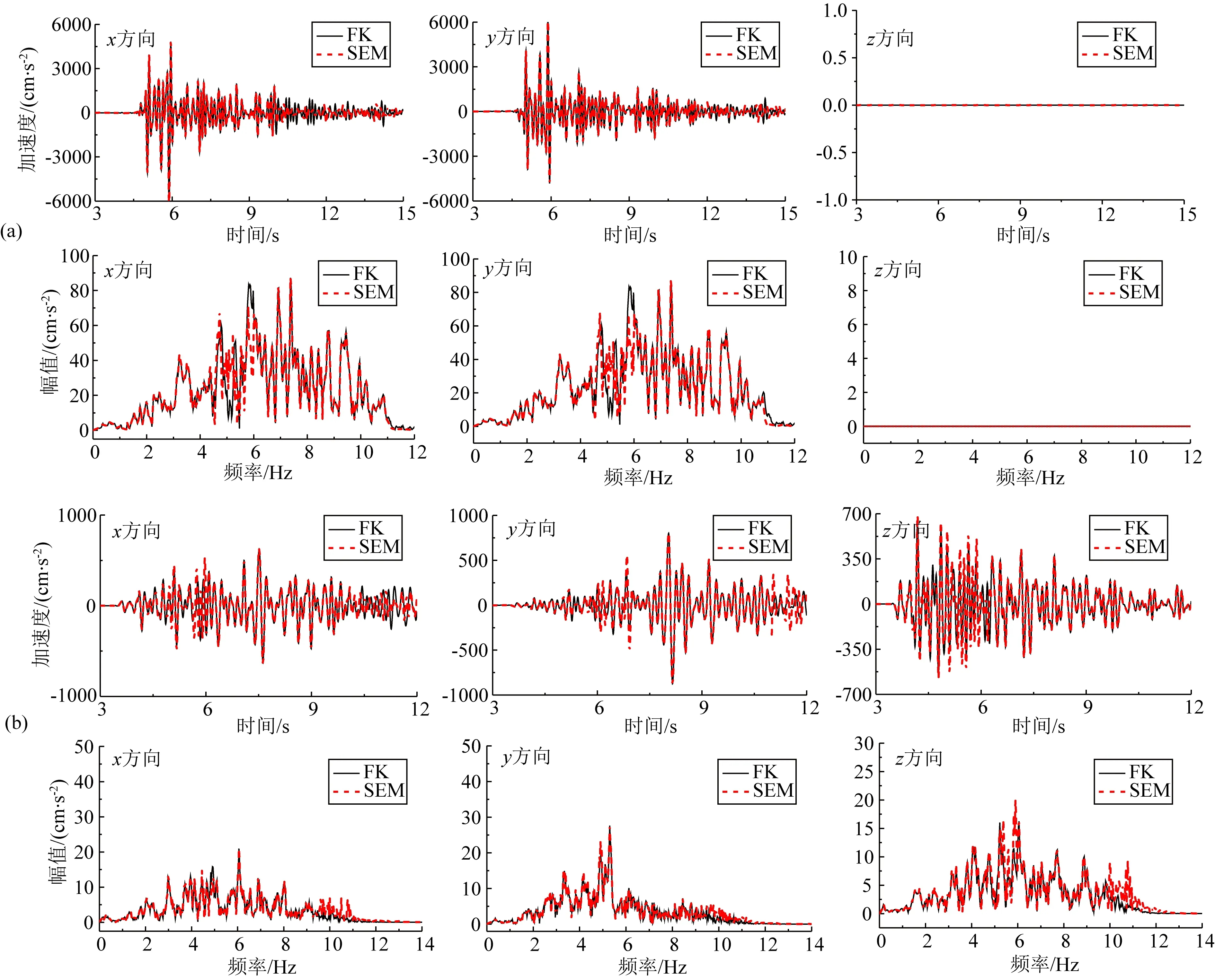
图6 P1(a)和P2(b)多层一维波速结构模型计算结果Fig.6 Calculation results of P1 (a) and P2 (b) multilayer 1D wave velocity structure models

3 适用性检验：2021年漾濞6.4级地震动模拟

为检验SEM模拟宽频地震动的适用性，本节选择模拟2021年漾濞6.4级(0～5 Hz)地震，将模拟结果与台站观测记录的时程和反应谱的比较，及与NGA-West2地震动衰减方程的反应谱曲线的比较，检验了方法的适用性.

2021年5月21日云南大理州漾濞县6.4级地震造成数十万人受灾，数万间房屋倒塌，直接经济损失高达33.2亿元.中国应急管理部将此次地震列为2021年全国十大自然灾害.根据中国地震局工程力学研究所提供的强震动观测数据，漾濞MS6.4地震共触发28个自由场强震动观测台站，除053YPX台站只获取了两个水平分量的记录外，其余台站均获得了完整的三分量强震动加速度记录.基于上述丰富地震记录，许多学者和研究人员开展了近断层地震动模拟特征的相关研究，何欣娟和潘华(2021)采用随机有限断层法模拟了目标区域峰值加速度的分布；周红等(2021)采用NNSIM随机有限断层法模拟了近断层200 km范围内的峰值分布特征；强生银等(2021)基于随机有限断层三维地震动模拟方法，给出了漾濞地震中28个强震动台站的三分量加速度时程模拟结果.上述模拟方法大多数选用随机方法进行模拟，由于随机方法仅能合成一维水平分量的高频地震动并且无明确方位.本节采用GP14.3震源模型和SEM对该地震进行0～5 Hz地震动模拟，模拟计算区域见图7所示，其中模型经度范围99.4°E—100.4°E、纬度25.4°N—26.0°N，区域范围内包含053YBX、053DLY、053YPX和053BTH台站.根据目标区域得到计算模型沿东西长约100 km，南北宽约60 km，纵向约30 km.本文以“中国大陆浅层结构模型”和“中国大陆岩石圈速度结构模型”为主，参考CRUST1.0，并依据漾濞地区的地面高程数据，构建了包含起伏地形的三维速度结构模型，包含介质的压缩波速VP、介质的剪切波速VS，质量密度ρ、品质因子Q以及层厚度等，具体参数见表3所示.

图7 漾濞地震模拟区域Fig.7 Yangbi seismic simulation area

表3 漾濞地区速度结构参数Table 3 Velocity structure parameters of Yangbi area

本文设定能模拟的最大频率为5 Hz，网格总数约为1169×104，GLL节点数量高达7.65×108个，时间步距取为0.005 s，模拟90 s内的地震波传播，采用国家超算“天河一号”400核计算耗时7.2 h.

基于1.2节的GP14.3混合震源模型建立漾濞地震的混合运动学震源模型参数包括全局震源参数和局部震源参数.本文的全局震源参数采用张斌等(2021)研究给出的包括断层面的几何信息、产状(走向角、倾角及上边缘埋深)及破裂方式(破裂形式和滑动角)等，具体见表4.将断层面划分为15×15个1.0 km×1.0 km的矩形子源.震源局部参数(主要是凹凸体模型参数)基于局部参数定标率确定，因本次地震震级小于6.5级，断层面上仅采用单凹凸体，具体局部参数及定标率见表5.根据1.2节公式计算断层面各个子源的时空分布，得到漾濞地震混合运动学震源模型见图8所示.

表4 漾濞地震断层全局震源参数Table 4 Global source parameters of the Yangbi earthquake fault

表5 漾濞地震断层局部震源参数Table 5 Local source parameters of the Yangbi earthquake fault

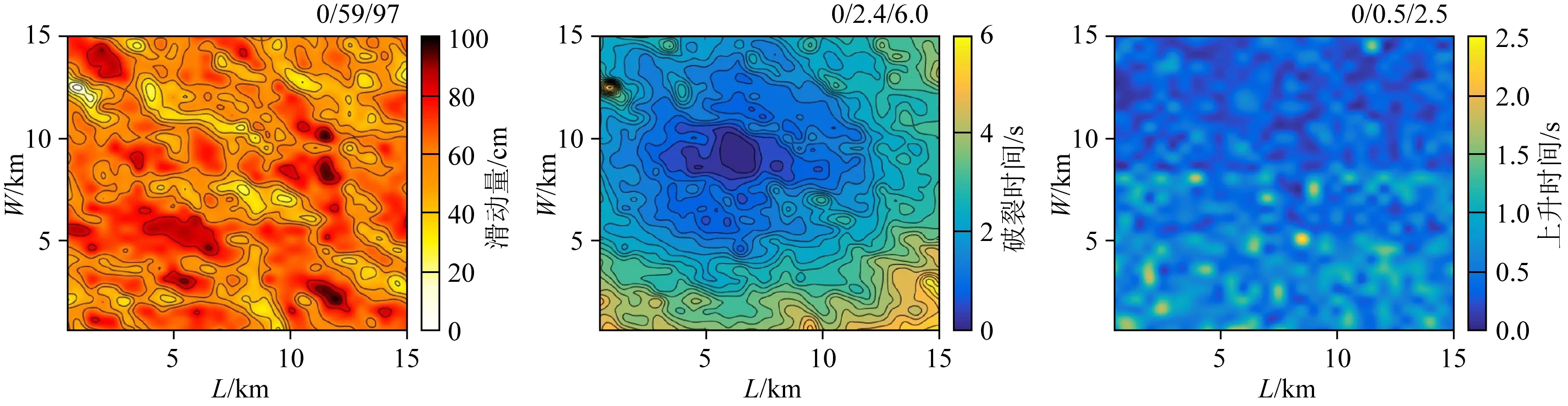
图8 漾濞地震混合运动学震源模型每个子图右上角的数字三值组分别表示给定分布的最小值、平均值和最大值.Fig.8 Hybrid kinematic source model of the Yangbi earthquake Triplet of numbers at top right of each panel indicates the minimum, mean and maximum values of the given distribution, respectively.

3.1 实际观测记录对比

图9给出了模拟区域内共4个台站的模拟结果与强震记录的加速度时程和反应谱的结果对比.其中反应谱结果左上角标注了每个台站的名称，黑线代表NS方向，红线代表EW方向，蓝线代表UD方向.反应谱结果下方为模拟结果与强震记录对应的加速度三分量时程结果，方向与反应谱结果的方向保持一致，上方为观测结果，下方为模拟结果.每条时程的持时均为50 s，PGA均标注于曲线的右上方，单位为cm·s-2.值得注意的是，图9中给出的强震记录已经带通滤波至0.1～5 Hz.对比结果表明：本文模拟的加速度时程的波形、持时和幅值与强震记录对比良好，特别是与震中距7.9 km的53YBX台站对比结果较为一致，并且模拟结果在周期0.2～5 s的PGA反应谱与强震记录吻合的PGA反应谱结果较为一致，总体上表明了本文提出的基于SEM进行宽频地震动模拟以及应用GP14.3的混合震源模型的针对实际地震模拟的适用性.由于本文建立的含起伏地表的地壳层波速结构模型，暂时未能考虑地表低波速土体对地震波的影响，故随着震中距的增加，速度结构对地震波传播的影响更加明显，导致震中距较远的台站记录与模拟结果差别相对明显.

图9 模拟与(YBXDLYYPXBTH)台站记录的加速度时程和反应谱(Sa)对比Fig.9 The simulation is compared with acceleration time histories and reaction spectra (Sa) recorded at (YBXDLYYPXBTH) stations

3.2 GMPE衰减方程对比

为了进一步对比各个周期下，特别是基于物理的宽频地震动模拟得到高频结果的适用性，本文将模拟结果与NGA-West2提供的地震动衰减关系曲线进行对比，对比结果见图10所示.其中，采用Dangkua等 (2018)基于地震动数据分析后，计算得到的适用于中国大陆地区的地震动衰减关系，即将NGA-West2中ASK14、BSSA14、CB14、CY14和IM14每个衰减关系均取0.2的权重计算得到地震动衰减关系.同时，为与上述衰减关系进行对比，我们将模拟得到的两个水平正交分量(NS和EW)分量的加速度时程在水平面进行旋转，计算0°～90°范围内每旋转θ角度后的加速度时程，将不同周期下各水平分量的反应谱值作几何平均并求其中位数得到GMRotD50.将模拟结果得到不同周期下GMRotD50结果随距破裂顶部边缘的水平距离Rx(km)的变化与周期0.2～5 s的GMPE衰减方程进行对比，图中红线代表反应谱结果的平均值，上下两条黑线分别代表±σ的误差范围.对比结果显示，在0.2～5 s的周期内高、低频的模拟结果与衰减关系曲线均取得了良好的一致性，进一步说明了上述模拟方法的可靠性.

图10 不同周期下模拟的加速度反应谱RotD50结果和GMPE曲线对比结果PSa是伪加速度反应谱，σ是标准差，Rx是沿垂直于断层走向方向、观测点到断层顶面的距离.Fig.10 The results of simulated acceleration response spectrum RotD50 are compared with the GMPE curves under different periods PSa is pseudo spectral acceleration, σ is standard deviation, Rx is horizontal distance from top of rupture measured perpendicular to fault strike.

根据上述地震动时程、峰值、反应谱以及衰减关系的充分比较分析，验证了本文提出方法的可靠性，总体上说明本文采用的SEM和混合震源模型适用于2021年漾濞6.4级地震的宽频地震动模拟，同时，通过模拟给出了2021年漾濞地震下区域的峰值地震动空间分布特征，见3.3节所示.

3.3 地面运动峰值PGA和PGV分布

图11(a，b)分别是目标区域的水平方向峰值加速度(PGA)和峰值速度(PGV)分布图，水平分量由NS分量和EW分量通过矢量合成方式获得.观测图中峰值较大区域集中在断层投影面附近，这与混合震源模型中凹凸体的位置相对应，体现了近断层地震动的集中性效应；垂直于断层走向的PGA和PGV比平行于断层方向的衰减更快，这是由于断层呈中心破裂，释放的能量持续在破裂前端汇聚，体现了近断层地震动的破裂方向性效应.

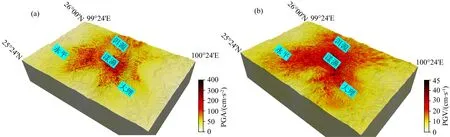
图11 地震动PGA(a)和PGV(b)分布图Fig.11 Distribution of ground motion PGA (a) and PGV (b)

研究区域PGA分布形态，震中点临近漾濞县城，最大值接近400 cm·s-2，在近断层区域，整个断层位置区域，PGA均高于300 cm·s-2，随着震中距的增加，地震动出现快速衰减，区域内从300～50 cm·s-2衰减迅速，在永平县附近PGA低于50 cm·s-2.观察区域内PGV分布发现，极震区PGV接近45 cm·s-1，漾濞县城范围内PGV达到40 cm·s-1，区域内PGV比PGA的衰减相对缓慢，永平县附近PGV达到20 cm·s-1.同时值得关注的是，由于地表起伏的影响，PGA和PGV的峰值分布出现明显的不均匀性，特别是大理和洱海西侧位置受局部凸起地形的影响导致地震动能量聚集，放大了地震动响应，上述地区出现的高烈度异常现象值得注意.

4 结论

本文将GP14.3有限断层混合运动学震源开发到SPECFEM 3D开源代码中，实现了基于确定性物理模型的全过程宽频带地震动模拟.文中首先根据定标律建立了凹凸体震源模型，进而通过在断层面的滑动分布中结合Graves & Pitarka提出的GP14.3随机震源模型得到混合运动学震源模型.最后将上述混合运动学震源模型计算得到每个子源的矩张量以及对应的时间函数按照对应格式输入到SPECFEM 3D谱元程序中.

为检验该方法的精度和可靠性，文中分别建立一维(均匀和多层)和漾濞地区的波速结构模型以及对应的混合运动学震源模型，将得到的SEM模拟结果分别与FK方法的计算结果和2021年6.4级漾濞地震记录进行对比，并且论文最后还给出了漾濞地震下近场强地面运动的空间分布特征.主要结论如下：

(1)针对均匀和多层一维波速结构模型，SEM模拟结果与作者建立的FK方法的计算结果在宽频带(0～10 Hz)吻合良好，验证了提出方法的精度;针对云南漾濞6.4级地震，模拟结果与区域内4个台站观测记录的时程和反应谱的结果接近，并且模拟得到地震动衰减规律与NGA-West2地震动预测方程在频率0.1～5 Hz的反应谱结果具有较好的一致性，检验了方法的适用性.

(2)2021年漾濞地震震中PGA接近400 cm·s-2，PGV达到45 cm·s-1，极震区烈度最高可达到Ⅸ度，并且受局部地形起伏影响，大理以及洱海西侧位置出现了高烈度异常区.

致谢感谢中国地震局工程力学研究所为本研究提供了2021年5月21日漾濞6.4级地震近场区域的地震观测记录．感谢国家超级计算天津中心“天河一号”为本文计算提供的帮助．感谢三位匿名审稿专家对本文提出的修改意见.感谢Dimitri Komatitsch和Jeroen Tromp等人提供的Specfem3D_Cartesian谱元法计算程序，程序的下载网址为(https:∥github.com/geodynamics/specfem3d.git).