三维各向异性裂缝介质正演模拟的三种交错网格适应性比较及Lebedev方法的改进

徐云贵， 廖建平， 周林， 刘和秀， 张青， 谢敬涛, 王立歆

1 西南石油大学地球科学与技术学院, 成都 610500 2 西南石油大学油气藏地质及开发工程国家重点实验室, 成都 610500 3 湖南科技大学地球科学与空间信息工程学院, 湖南湘潭 411201 4 中石化地球物理重点实验室, 中石化南京物探研究院, 南京 211103 5 重庆科技学院非常规油气开发研究院， 重庆 401331

0 引言

地下岩石中的天然裂缝可形成流体的有效通道或储集空间，而含裂缝岩石的物理性质因流体的存在和流体的流动发生变化.为了解含流体裂缝岩石的物理性质以及其中的流体流动特性，首先必须研究裂缝本身属性(Li, 1999).在地震波动力学中，岩石裂缝的存在影响地震波传播方式，一种有效的研究裂缝方法是通过地震正演模拟来研究裂缝系统的地震响应，并与现场采集的实际地震资料进行比较，以确定裂缝空间发育规律(Tsvankin et al., 2010).裂缝介质地震正演模拟在裂缝研究中具有两个重要的作用：一是揭示各种裂缝介质对应的地震响应规律，二是验证现有裂缝反演方法的有效性(Liu et al., 2000; Mavko et al., 2009).但到目前为止，很多裂缝反演和正演模拟研究都局限于二维情况(Nihei et al., 2002; Vlastos et al., 2003; Vlastos, 2005; Rao and Wang, 2009).三维裂缝介质中地震正演模拟因存在计算量大等问题限制了其应用规模.然而，裂缝介质的三维地震响应研究意义重大，三维地震数据更能体现地震波在真实意义的三维各向异性介质中的传播机理，从而能依据各向异性理论和方法来表征裂缝空间发育规律.一个典型的例子是，在地震勘探中基于三维实际叠前地震纵波数据，通过分析地震波振幅或速度的方位各向异性来反演高角度裂缝密度，提高对高角度裂缝空间发育规律的认识.

裂缝介质的地震正演模拟大多采用有限差分方法(Finite Difference，简称FD).Willis等(2006)和Grandi-Karam (2008)进行了三维离散裂缝模型(Discrete Fracture Model，简称DFM)的正演模拟研究.他们讨论了DFM模拟数据如何利用散射波确定裂缝方向和裂缝间距，其研究内容使用现有有限差分工具实现三维FD正演模拟，并未讨论模拟方法的具体实现过程.本文将讨论裂缝介质中FD正演模拟的更多细节，譬如正演模拟实现、优化、模拟方法的选择等.

裂缝介质的FD正演模拟常采用三种交错网格方法.第一种是Virieux(1984,1986)提出的标准交错网格方法(SSG)(Levander, 1988; Dong and McMechan, 1995; Graves, 1996; Liu, 2014; Ekanem and Xu, 2018).在SSG方法中，将波场分量离散到不同的数值网格中，计算所需网格位置的波场空间导数，迭代求解波动方程，即得到模拟结果.SSG方法简洁且容易编写程序实现，能有效计算正交各向异性介质模型.第二种是Saenger等(2000)提出了旋转交错网格方法(RSG)，该方法通过组合网格对角线上的波场分量求解空间导数，有利于处理任意复杂各向异性介质模型，但相对SSG方法，RSG方法计算资源耗费更高(Saenger和Bohlen，2004).第三种是Lisitsa(2007)将Lebedev格式(LS，Lebedev, 1964)引入地震正演模拟，波场分量呈菱形分布在FD网格中，可沿坐标轴求解空间导数，Lebedev格式也是一种交错网格方法(Lisitsa et al., 2009；Lisitsa and Vishnevsky，2011；Lisitsa et al., 2012a；Lisitsa et al., 2012b；Vishnevsky et al., 2014；Quintanilla and Leckey，2018；Koene et al., 2021a; Koene et al., 2021b).Lisitsa 和Vishnevskiy(2010)定量比较了任意各向异性介质中的RSG和LS方法.然而，三维地震正演模拟需要厘清不同的FD交错网格方法在模拟各种各向异性介质(如TTI和正交介质)中的适用性，因为不同的各向异性介质刚度矩阵形式不同，矩阵形式决定交错网格方法的选取和计算资源的耗费大小.这一点非常重要，特别是在三维模拟的情况下，大型三维各向异性模型的正演模拟通常需要几天、几周甚至长达数月.这种对比研究有利于方法的选择和计算过程的优化，在基于各向异性正演模拟的地震资料处理和解释时尤为重要(Liao et al., 2022; Wang et al., 2022)，如逆时偏移 (RTM, Reverse Time Migration, Shi et al., 2019) 和全波形反演(FWI, Full Waveform Inversion, Guo et al., 2019).

国内的学者们对Lebedev方法进行了深入的研究，并成功应用于地震波数值模拟中.李娜等(2014a)实现了Lebedev网格与标准交错网格耦合机制下的复杂各向异性正演模拟的研究.李娜等(2014b)进行了Lebedev网格改进差分系数TTI介质正演模拟方法研究.黄建平等(2016)开展了基于M-PML边界的Lebedev网格起伏地表正演模拟方法及稳定性分析的研究.杨宇等(2016)实现了Lebedev网格黏弹性介质起伏地表正演模拟.黄金强等(2017)实现了TTI介质Lebedev网格高阶有限差分正演模拟及波型分离.刘东洋等(2018)基于Lebedev网格的TTI介质二维三分量正演模拟，引入多轴完全匹配层(M-PML)吸收边界条件后，在不影响模拟效果的情况下边界反射现象被有效地压制.胡书华等(2018)进行了TTI介质稳定的纯qP波波场模拟方法研究，他们在Lebedev交错网格框架下推导了高阶有限差分方程，并给出2次计算波场梯度的数值算法，以保证波场模拟精度.

三种交错网格求解波场空间导数的不同求解方式决定了它们对特定类型各向异性介质的模拟的能力.SSG很容易模拟简单各向异性介质(VTI，HTI，正交各向异性)，而其他两种方法可以处理任意各向异性介质，但计算成本较高(Xu and Wang, 2017).本文比较了三种主要有限差分交错网格方法，厘清了每种方法的优势和局限，提出了一种优化的正演模拟计算流程，并改进了LS方法的数值实现.通过二维与三维合成实例验证了该方法的正确性与稳健性.

1 理论

1.1 三维弹性各向异性波动方程的速度-应力公式

地震各向异性模拟基于各向异性弹性波动方程，波动方程可用一阶速度-应力关系描述，包括胡克定律(方程(1))和牛顿第二定律(方程(2))：

(1)

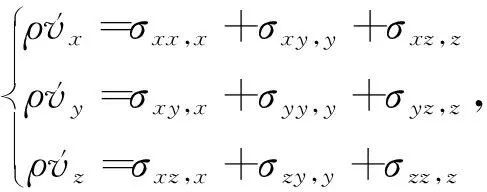
(2)

1.2 各向异性介质中的地震正演模拟的三种交错网格

有限差分求解上述波动方程主要有三种不同的FD交错网格方法(SSG，RSG和LS)，使用交错网格是为了实现基于中心差分求解空间导数，三种交错网格方法的共同特征是：(1)正演模拟中至少有两个FD交错网格；(2)一个网格位于另一个网格的中点处，确保可以基于中心差分求解空间导数；(3)有限差分求解空间导数时，只在导数位置处使用相邻的几个点的波场分量或模型变量，计算效率高.

以下详细讨论三种方法在模拟各种各向异性介质模型的优势和局限.

1.2.1 SSG方法

Virieux(1984, 1986)做了较早的SSG研究工作，用于求解二维各向同性介质中的地震波传播问题，SSG中有4种不同的相互交错的网格参数(如图1a).二维SSG方法由Dong和McMechan(1995)扩展到三维黏弹性各向异性正演模拟，涉及7种不同的网格(图1b)，这里和后面提到的分量或参数见方程(1)和(2).不同的波场分量或模型参数都分布在交错的网格上，以便使用中心差分来求解速度或应力的空间导数，三维模型的7种网格交错分布的特定位置是SSG方法的特点.SSG方法容易实现、计算速度快、计算成本低，因此大多数正演模拟都是基于SSG方法.SSG方法在处理垂直对称轴的横向各向同性(VTI)介质、水平对称轴的横向各向同性(HTI)介质和正交介质时都表现良好，因为这些介质的刚度矩阵c的非零常数分量可以放在图1b的1位置，便于求解中心差分导数.三维SSG的四个特点是：(1)SSG方法包括7种交错的网格(见图1b中的矩形和圆形编号为1—7的网格)；(2)计算速度快，内存成本小；(3)能够很好地处理各向同性、VTI、HTI和正交介质；(4)比正交各向异性更复杂的介质(TTI、单斜和三斜介质)的正演模拟，需要对波场进行插值(牟永光, 裴正林, 2005).例如，TTI、单斜和三斜介质中的正演模拟，速度分量需要插值，从而导致产生误差.因此，尽量采用其他的交错网格方法去避免插值.

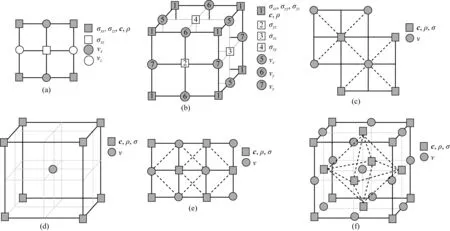
图1 三种不同的交错网格(a) 二维标准交错网格； (b) 三维标准交错网格； (c) 二维旋转交错网格； (d) 三维旋转交错网格；(e) 二维菱形交错网格； (f) 三维菱形交错网格.Fig.1 Three staggered-grids The SSG in 2D case (a) and 3D case (b), the RSG in 2D case (c) and 3D case (d), and the LS in 2D case (e) and 3D case (f).

1.2.2 RSG方法

为了能够适应更复杂的各向异性介质的模拟，Saenger等(2000)引入了一个新的有限差分交错网格实现方法，即RSG，在二维或三维时，只有2种交错的网格(图1c和图1d).网格越少，方法实现越简单，所有的速度分量在一个交错网格点上，所有的应力分量在另一个网格上.不同的是，在求解应力分量的空间导数时(例如在图1d中圆形位置的应力空间导数)，需要输入该导数位置周围的4个对角线网格点上的8个应力分量(8个矩形)的线性组合；在求解速度分量的空间导数时，则需要这些网格点上的速度分量组合.此特点可以实现任意各向异性介质中地震正演模拟(包括TTI、单斜和三斜介质)，而不需要对波场分量进行插值.该方法的缺点是求解空间导数时，需要对角线上的4个分量参与计算，导致计算量比SSG大很多.此外，由于使用对角线分量计算导数，对角线的长度作为求导的单位长度，为了保持与SSG方法相同的精度，RSG模型的单位体积内需要更多的网格点和计算量.RSG的四个特点是：(1)模型中只有矩形和圆形两种网格，简化了模型；(2)比SSG方法需要更多的计算和内存需求；(3)可以很好地处理任意各向异性介质；(4)需要线性组合对角线的波场分量求解空间导数.

1.2.3 LS方法

方程(1)和(2)的重要特点是：方程右边波场分量的中心差分的空间导数乘以密度或刚度常量，如果落在方程左边分量的位置，可以利用交错网格来解方程(1)和(2)，否则需要插值.在三维LS中，取一个分量，将另外一个分量布置在该分量的上下、前后和左右的6个位置(组成菱形形状)，则可以完全满足交错网格的要求，而且对于任意介质的刚度矩阵都适用.因此，LS方法适用于任意各向异性介质的波场正演模拟.

在LS方法中(图1e和图1f)，相同的场分量组成菱形网格(图1e和图1f的虚线的对象)，这些网格的特点是：可以在不对波场分量插值的前提下，利用中心差分方法在期望的网格位置处求取所有的导数，因而可以模拟任意各向异性介质，它不同于SSG中的元素需要插值，也不同于RSG中的导数组合.例如，在图1f中虚的菱形网格，三个速度空间导数沿三个轴，在三维菱形的6个顶点处，可以用6个速度分量在菱形的中心处求解三个速度导数.应力空间导数求取与此相同.因而，LS在数值实现上更加直接而且更容易理解.

从图1e和1f可以看出菱形网格中，每个单元网格有更多的分量网格节点，因此需要更多的计算内存，同时更多的分量网格会导致更多的计算时间.由于计算机适合处理使用二维/三维规则矩形网格，这种不寻常的菱形特性会给正演模拟数值实现带来困难.LS方法的优点是网格少，只有两个网格，处理简单，在任意各向异性介质中正演模拟时，不需要SSG方法中的插值，也不需要RSG方法中的波场分量的线性组合.LS的四个特点是：(1)只涉及两个网格(矩形和圆形两种网格)；(2)与SSG相比，计算量更多，存储成本更高，但均比RSG低；(3)能够更好地处理任意各向异性介质；(4)网格是菱形.

在任意各向异性介质中，方程(1)和方程(2)的第一个表达式的离散LS形式为

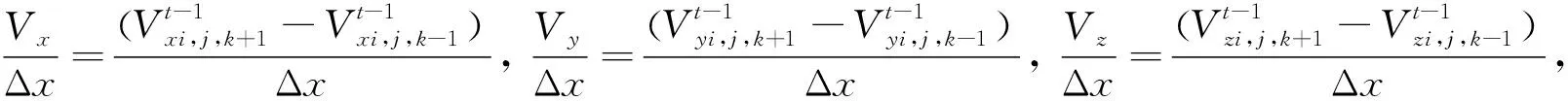
参数与方程(1)、(2)相同.

当i+j+k为奇数时，

(3)

当i+j+k为偶数时，

(4)

值得注意的是，方程(3)和方程(4)的假设是奇数与偶数条件，这里符号参数与方程(1)和(2)相同.

总之，对于三种交错网格，在定义应力分量的位置上用中心差分求解速度分量的导数，反之亦然.SSG网格数比RSG和LS多.RSG在网格的对角线求解波场的导数.LS沿坐标轴求解波场导数，但导致非矩形网格，即菱形网格.

1.2.4 三种方法的定量比较

以上定性讨论了三种交错网格方法的适用性问题，为定量确定各种方法在模拟时的真实计算量和计算机内存消耗，以下按图2所示的三维单元网格为基础展开讨论.

图2 三种方法中的单元格(a) SSG； (b) RSG； (c) LS.由于交错网格的原因，这里单元格的长度是网格间距的一半.Fig.2 Unit cells in the three schemes: SSG(a), RSG(b) and LS(c) Note the length of the unit cells here are half the cell spacing due to the staggered-grid.

为了有效对比三种方法，以同样几何尺度的正交各向异性模型为例，并且以同样的精度为基准.通过比较最终的内存消耗和计算量，就可以确定每种方法的计算适应性特征.以下进行详细讨论与比较(参考表1)：

表1 相同大小模型、相同精度条件下三种方法的计算机内存消耗和计算量比较Table 1 Memory cost and computation for the three scheme when the model with the same size and the same accuracy are considered

(1)首先讨论三维SSG方法的计算要求.假设模型大小为n×n×n(n为每个边的样点数，单元网格边长相等)，参考图2a，共有7种可能的交错网格，对应11个波场和模型变量，内存消耗量为n×n×n×11.在模拟过程中，计算量主要取决于空间导数的计算，因此可以利用求解导数的次数确定计算量的大小，依据方程(1)和(2)，SSG方法中一个单元网格(如图2a)需要求取18次空间导数，即总计算量为n×n×n×18.

(3)若要达到相同的精度，LS方法在每个单元网格上所需的变量网格数是4(如图2c，网格点为4)，故三维模型共需要n×n×n×4个网格点，涉及11个波场变量和模型变量，内存消耗量为n×n×n×4×11，共须求取18次空间导数，总计算量是n×n×n×18×4.

综上所述，对于SSG、RSG和LS而言，内存消耗比例为1∶5.2∶4，计算量大小比例为1∶20.8∶4，由此可见，SSG计算效率最高，LS其次，RSG最低.SSG只能有效模拟简单各向异性介质(各向同性、VTI、HTI和正交各向异性)，RSG和LS则可以模拟任意复杂的各向异性介质(TTI，单斜和三斜介质).对于复杂的各向异性介质，LS消耗的内存和计算量相对RSG较小，因此LS方法更适合模拟复杂各向异性介质模型.

2 改进后的LS实施方法

Lisitsa和Vishnevskiy(2010)给出了任意各向异性介质中使用LS方法进行正演模拟的详细描述.然而，他们并没有直接描述将其应用于实际正演模拟时如何处理菱形网格.

图1都是FD交错网格的空间结构，每个图中显示了所有波场速度分量和介质参数的相对空间位置；在计算实现时，每个分量或介质参数由2D或3D数组表示；对LS方法，如图1(e、f)，每个分量或参数都是菱形，但在这种LS方法中，由于网格为菱形，所以不便于保存这些矩形数组中的元素或参数，导致菱形网格有一半的网格点没有存储任何变量，即有一半内存占用但是并未使用.本文提出合并速度分量和应力分量，形成新的网格.例如，一个速度分量和一个应力分量合并形成一个矩形的二维或三维数组，以保持数组中的每个元素被充分利用，不额外增加内存消耗.根据我们的研究，菱形网格在实施过程中，可以特殊处理：两个不同的菱形网格可以合并形成一个规则的矩形，以处理所有的波场分量.

这里详细说明LS的简化实现过程.基于三维空间中的LS(图1f)，将所有的σ网格和网格v结合形成新的网格T.因此在三维模型每个网格位置都有一个矩形形状的T(如图3所示).这样一个组合的条件是，如果i+j+k的和为奇数，T(i,j,k)代表应力分量；如果i+j+k的和为偶数，则T(i,j,k)代表速度分量.反之亦然，如果i+j+k的和为偶数代表应力分量，i+j+k的和是奇数代表速度分量.上述表述的优点在于，如果方程(5)的三个表达式中的T表示速度分量，则其空间导数即三个表达式的结果正好位于应力分量的位置.其优点是使用奇数与偶数条件，方程(5)可以用来近似三个坐标轴上的应力分量或速度分量的空间导数.

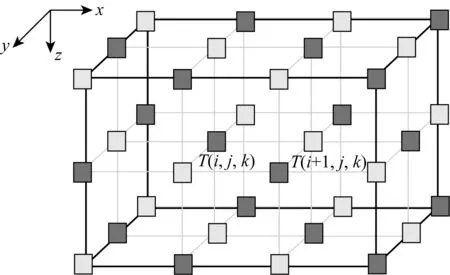
图3 改进的LS数值实施方法两个网格合并成一个新网格.极大地简化了使用新网格的下标而计算导数.Fig.3 The modified implementation of the LS scheme, where two grids are merged into one This greatly simplifies the calculation of the derivatives with the subscripts of the new grids.

(5)

另外，SSG的实现涉及到多个波场分量，而RSG的实现需要组合多个波场分量.为了实现SSG和RSG，须清晰地确定每个波场分量的空间确切位置；而对于LS，使用方程(5)和奇数与偶数条件，无需参考空间相对位置，比如，当需要求取(i,j,k)位置的三个空间导数，总能通过所在菱形的6个顶点元素来实现中心差分导数的求解.基于这种方式，LS方法是这三个方法中实现各向异性介质模拟的最简单有效的方法.

3 模拟流程、震源设置和吸收边界条件

3.1 优化的模拟流程

鉴于LS法在任意各向异性介质模拟方面的优越性能，本研究以LS法为基础，开展三维FD数值模拟研究.

在三维各向异性介质正演模拟时，计算量和内存开销是三维正演模拟时必须关注的两个重要方面.三维各向异性正演模拟多数应用情况下(如基于AVO分析和岩石物理的各向异性研究中)，模型由几个层或块组成.基于层和块的组成条件，三维模型可使用不同的索引来区分不同的层或块(这里的索引可称为介质构造参数).在模拟计算过程中，依据索引取得介质的弹性参数.因此，可将9个弹性常数和1个介质密度合并成1个介质构造参数，加上9个波场变量，共需10个三维变量，约为原始19个变量的一半，并且复杂度显著降低.

本文提出了一种新的适用于三种交错网格有限差分格式的优化正演模拟计算流程，如图4所示：首先，定义三种参数类型：介质构造参数(索引)、介质弹性参数和正演模拟参数；其次，这些参数被输入到方程(1)的右边，以求解速度导数；然后，用这些速度导数和前一个时间步的应力分量求解方程(1)左边的应力分量，用求解的应力分量求解方程(2)右边的导数，代入方程(2)的左边，计算速度分量；最后，在地震检波器位置输出速度分量作为地震记录.在每次循环过程中，考虑边界条件和震源设置.在图4的工作流程中，将介质参数分为介质构造参数和介质弹性参数的原因是，在建立比较大的三维模型时，能有效节省计算机内存.

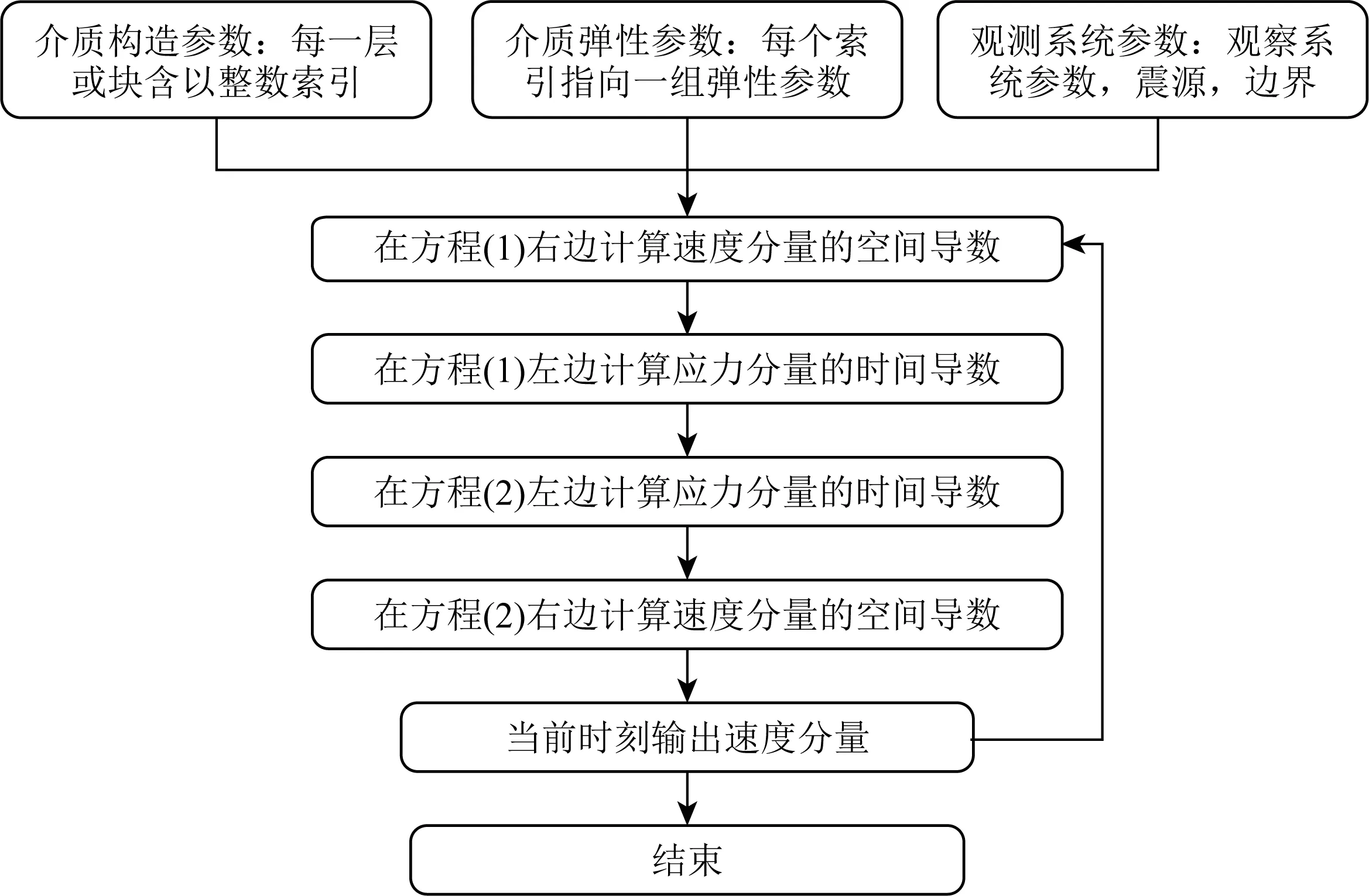
图4 优化的三维正演模拟工作流程Fig.4 The optimized 3D modelling workflow

3.2 震源设置和吸收边界条件

三个交错网格方法存在差异，但对于震源设置来说，均可在邻近震源网格处添加Ricker子波的爆炸震源来实现(方程(12)，Sheriff，2002)，将子波的振幅添加在正应力之上(二维情况正应力为σxx和σzz，三维情况正应力为σxx,σyy和σzz)，表2给出了具体每种方法震源施加的位置.Ricker子波形式为

r(t)=[1-2(πft)2]e-(πft)2,

(6)

其中，f表示子波主频，t是时间，[1-2(πft)2]是子波振幅值.

一旦触发震源，地震波将从震源位置开始向四周传播，如果传播时间足够长，波场将遇到模型边界并发生反射.通常而言，来自模型边界的反射是无用信号，故须对边界能量进行处理.我们选择吸收函数衰减在二维/三维模型边界的能量.声波或各向同性介质模拟通常使用PML边界条件，在本研究中三维各向异性介质的模拟涉及到参数众多，计算量巨大，如果使用PML边界条件，计算量会增加数倍，因此从实用性的角度出发，最终选取了常用的“海绵”吸收边界条件(Cerjan et al.，1985).本研究应用“海绵”吸收边界条件，使用厚度为20个网格，吸收边界使用的函数方程如下：

表2 不同FD格式下应用法向应力震源子波的网格位置Table 2 Grid locations to be applied to the source wavelet on the normal stresses in different FD schemes

G=e-[0.015(20-i)]2,

(7)

其中，i是离边界网格点标号.

4 实例比较和三维算法验证

首先在二维情况下实现这三种方法，以便了解它们在地震正演模拟中的优缺点.用不同的FD方法在不同的各向异性介质中进行了一系列二维试验，并且将3D结果与反射率方法进行对比以验证新方法的精度.

4.1 使用SSG、RSG和LS的二维地震正演模拟

4.1.1 每种方法的潜力

图5a和5b分别展示了两个具有SSG和RSG的各向同性正演模拟示例.所有模型参数相同，只有方法(SSG或RSG)不同.介质参数为：纵波速度3500 m·s-1，横波速度2000 m·s-1，密度2.2 g·cm-3.爆炸震源位于模型中心；时间间隔为1 ms；Ricker子波的主频为40 Hz；记录时间为0.35 s；模型尺寸为600×600，网格尺寸为5 m×5 m.所有的模型参数相同，但方法不同.在图5b波前面内，出现了许多类似于散射波，这是由数值频散引起.正如预期的那样，在二维各向同性介质的波场快照中纵波的波前是个完美的圆.图5b中波前内观察到更多的数值频散.其原因是在RSG中，为了保持与SSG或LS中相同的精度，频散关系需要更小的网格间距.图5c显示了从图5a和5b中两个红线位置提取的两条模拟曲线，其中的RSG方法对应的曲线存在数值频散现象.

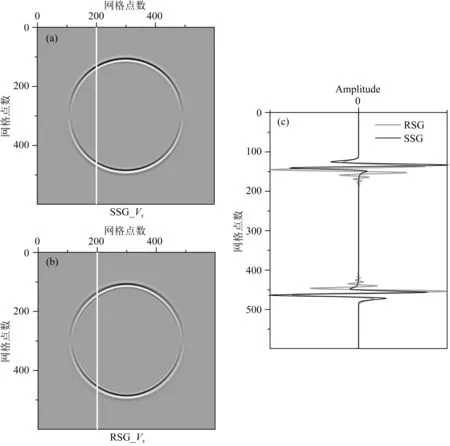
图5 各向同性介质中速度分量Z的波场快照SSG (a)和RSG (b)；(c)提取两个波场快照在第400垂直道位置的振幅曲线，绘制形成两条曲线(黑色曲线表示SSG的振幅，灰色曲线表示RSG的振幅)比较SSG和RSG的地震道，波动非常明显，但SSG准确性良好.Fig.5 Velocity Z-component snapshots taken with the SSG (a) and RSG (b) in an isotropic medium, and two traces extracted from the locations Trace 400 in (a) and (b) are plotted in (c) The black curve in (c) represents the SSG component amplitude and the gray one in (c) represents the RSG component amplitude.

图6为两个使用SSG和RSG方法进行各向异性正演模拟的算例.图6a和图6b分别为SSG正演模拟VTI介质的X分量和Z分量波场快照.其中模拟参数是，网格尺寸500×500，爆炸源在每个模型中心，时间间隔为1 ms，Ricker 子波的主频为40 Hz，网格间距为5 m×5 m，记录时间为0.3 s，轴的单位为网格数.该VTI模型的Thomsen参数为α0=2.4495 km·s-1,β0=1.4142 km·s-1,ε=0.3333,δ=0.0885,γ=0.2500和ρ=1 g·cm-3.图6c和图6d分别为RSG正演模拟TTI介质的X分量和Z分量波场快照.TTI介质是由VTI介质通过逆时针绕Y轴旋转30°而产生.所有其他参数都相同.各向异性参数作为Thomsen参数给出.从图6c和图6d，可以在波场快照中清楚地看到旋转角度.在两个例子中，VTI和TTI介质，无论是纵波和横波的观察，纵波波前长轴指向系统平面方向.因为SSG和RSG的观测系统和参数都相同，而RSG的差分单元长度是单个网格对角线，因而更容易导致数值频散，如图6c和图6d所示.这两个例子表明，SSG能够有效处理各向同性、VTI、HTI和正交各向异性介质，而RSG能够处理任意复杂的各向异性介质，包括TTI、单斜和三斜介质.

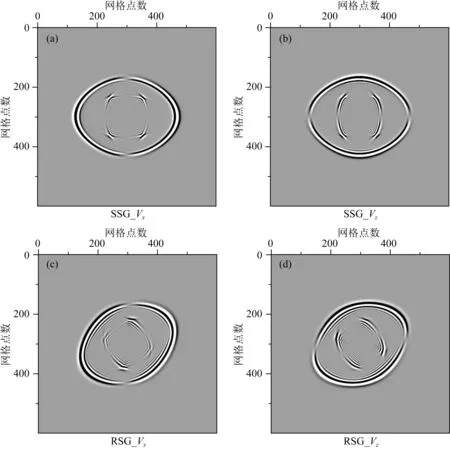
图6 RSG方法的速度分量波场快照(a)和(b)为使用SSG得到的VTI介质速度的x和z分量； (c)和(d)分别是(a)和(b)的VTI介质绕y轴逆时针旋转30°，即TTI介质，使用RSG得到的波场快照.Fig.6 Velocity component snapshots in RSG (a) and (b) are the snapshots of velocity component x and z respectively with the SSG in a VTI medium. (c) and (d) are the snapshots of velocity component x and z respectively with the RSG in the same medium as in the SSG but with a 30 degree anticlockwise rotation applied around the y-axis, namely, a TTI medium.

图7a和7b分别显示了VTI介质中的X分量和Z分量的波场快照.模型对应的Thomsen参数为，α0=3.368 km·s-1,β0=1.829 km·s-1,ε=0.11,δ=-0.035,γ=0.255和ρ=2.5 g·cm-3.图7c和7d分别显示了在TTI介质通过顺时针45°旋转图7a和7b的VTI介质产生的相应的波场快照，模型的尺寸是1000×1000；爆炸震源在每个模型中心；时间间隔为1 ms；网格间距为7 m×7 m；Ricker子波的主频为20 Hz；记录时间为0.5 s.图7中VTI和TTI模型模拟结果除角度差别外，振幅和形状一致可以证实二维LS方法的数值试验正确．两个例子中的频散关系相同，所以它们的精度相同.两个例子均表明LS能够模拟任意各向异性介质.在此，只演示了每种正演模拟方法的优势与缺点，尚未对其结果进行定量比较或验证.后续的三维模拟中，我们将通过与基于反射率法模拟结果的比较，来验证本文方法的有效性.

图7 使用LS方法的速度分量的波场快照(a)和(b)分别为VTI介质中得到的速度x分量和z分量； (c)和(d)为(a)和(b)代表的VTI介质绕y轴顺时针旋转 45°得到的TTI介质.Fig.7 Velocity component snapshots with the LS scheme (a) and (b) are the snapshots of velocity component x and z respectively in a VTI medium. (c) and (d) are the snapshots of velocity component x and z respectively with a 45 degree clockwise rotation applied around the y-axis, namely, a TTI medium.

4.1.2 矩形网格的正演模拟

在某些情况下，数值模型的网格边长不一定相等.更具体地说，网格沿x坐标的边长不等于沿y坐标的长度，也不等于沿z坐标的长度.用四个基于二维SSG和二维LS的例子演示了正演模拟，但网格边长不相等.对应的VTI介质模型参数VTI介质参数用Thomsen参数表示，α0=2449.5 m·s-1,β0=1414.2 m·s-1,ε=0.3333,δ=0.0885,γ=0.25，ρ=1 g·cm-3.模拟参数为，采样间隔0.001 s，记录长度0.27 s，主频率20 Hz的Ricker子波.模拟结果见图8.对于SSG方法，图8a采用10 m×10 m的网格.在10 m×5 m的网格下，图8b所示对应的地方被拉伸，正好是垂直长度的2倍.除拉伸外，图8a和图8b中的波场特征都是一样的，如振幅和相位.这证实了考虑矩形网格的SSG方法的有效性.LS方法生成图8c和图8d，除了模拟方法不一样之外，模拟和模型参数与图8a和图8b相同，其结果和图8a和b具有相同的特征和模式.

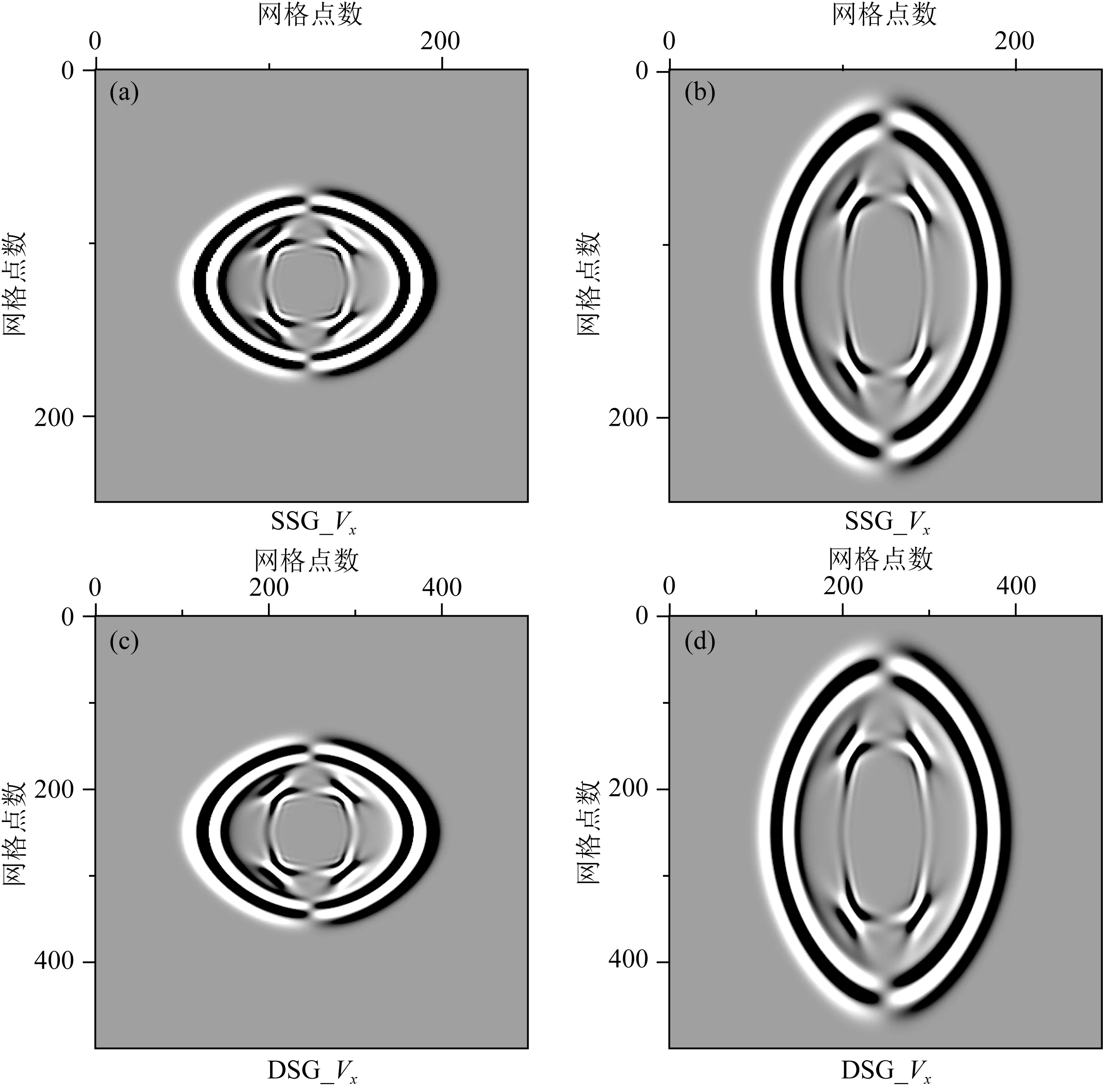
图8 四个矩形网格的SSG和LS方法数值试验SSG方法生成(a)和(b)两个样例， LS方法生成(c)和(d)另外两个样例.Fig.8 Four modelling examples with the SSG and LS methods (a) and (b) are generated with the SSG method, and (c) and (d) generated with the LS method.

4.2 三维地震LS正演模拟及算法验证

本文给出了一个三层模型的数值实现来展示新方法在3D条件下的优越性能，同时与反射率法(Kennett, 1983；Koketsu et al., 1991；Sen and Pal, 2009)进行对比，以验证本方法的正确性.

4.2.1 三维模型和模拟参数设置

图9显示了3层模型，中间层为HTI(或裂缝)层，其他两层为各向同性.表3列出了三层参数的详细信息.模型大小是1000 m×1000 m×2000 m，对应的网格数为101×101×201.震源(图9a中的加黑点)位于网格(0 m, 0 m, 0 m)，位于模型表面的角落.图9a地震检波器分布在模型表面的每个网格位置.其他模拟参数为，爆炸震源设置在网格点(0,0,0)，震源主频为15 Hz的Ricker子波，所有检波器与震源在同一深度，采样时间间隔为1 ms，记录长度为2 s.

表3 三维三层模型的参数Table 3 The parameters of the 3D 3-layer model

正如前文讨论过，层状或块状模型有助于在建立大型3D模型时节省计算机内存和提高计算效率.在实际工作中，存在一个包围整个三维模型的吸收边界层，用来将能量衰减到边界以避免边界的反射.在参数中没有考虑衰减层.震源为主频为15 Hz的Ricker子波.3D炮道集记录的时间长度为2 s.

4.2.2 结果与分析

从图9模型的三维炮道集抽取两个z分量剖面进行分析，道间距为20 m，图10表示X-Z剖面，图11表示Y-Z剖面，两者都通过震源位置.X-Z剖面平行于裂缝法向，Y-Z平面平行于裂缝走向.这里，为了便于对比分析，我们使用反射率法进行正演，提取对应位置的剖面.反射率法正演精度高，常用于验证其他正演方法的模拟结果，但是反射率法通常只适用于水平层状模型.图中黑色的波形(图10和图11)是我们使用LS正演模拟产生的剖面，红色的剖面是反射率法所产生的剖面.从图10和图11重叠的波形，我们可以看到无论是振幅还是相位，二者一致性非常好，这验证了我们的3D正演数值模拟准确.

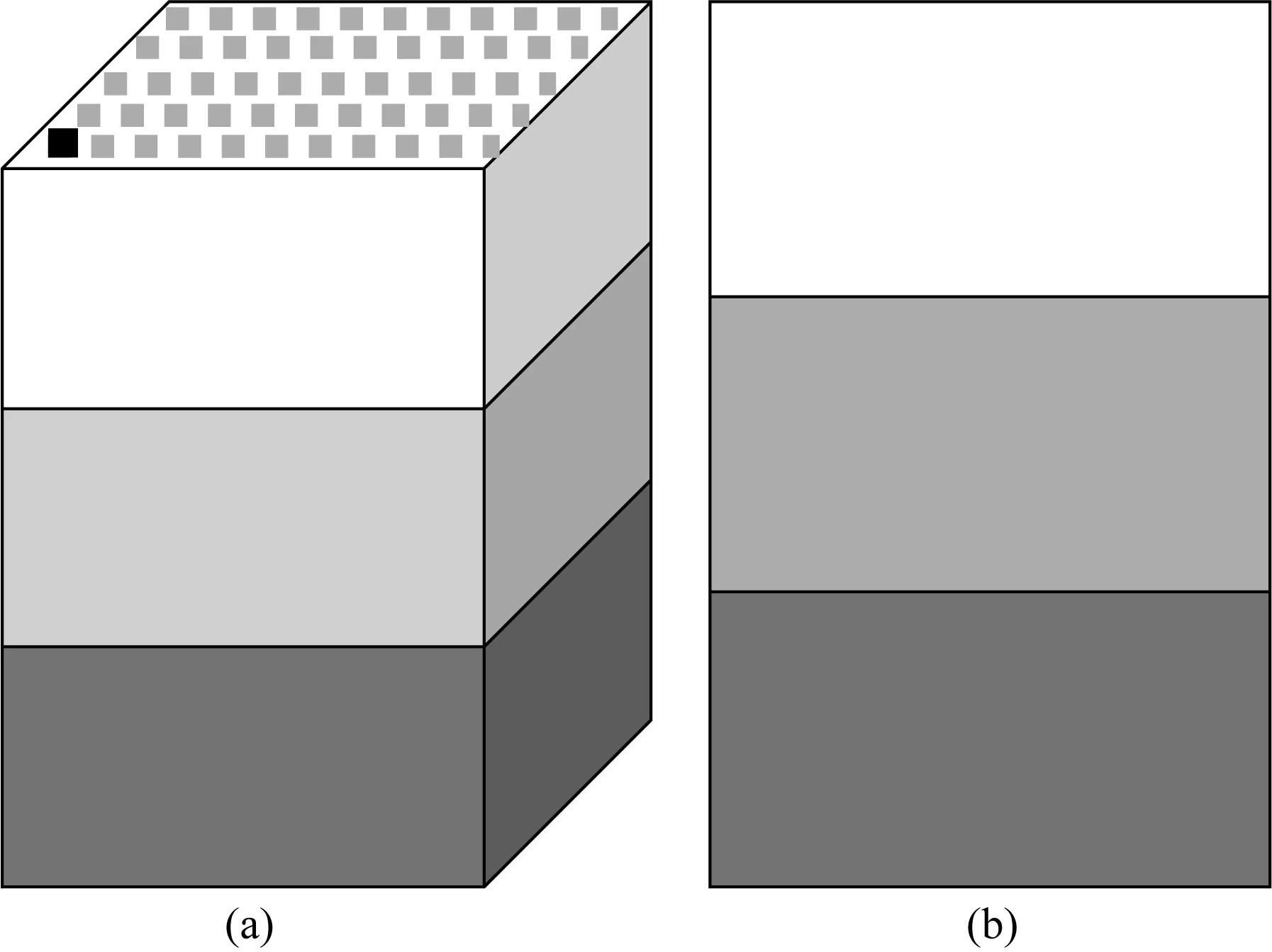
图9 (a) 模型网格数为101×101×201，网格间距为10 m×10 m×10 m的三维三层模型； (b)为X-Z平面显示层的厚度在二维模型剖面Fig.9 The 3D three-layer model (a) with the model size 101×101×201 and the grid size 10 m×10 m×10 m. The 2D section (b) in the X-Z plane shows the layers′ thickness

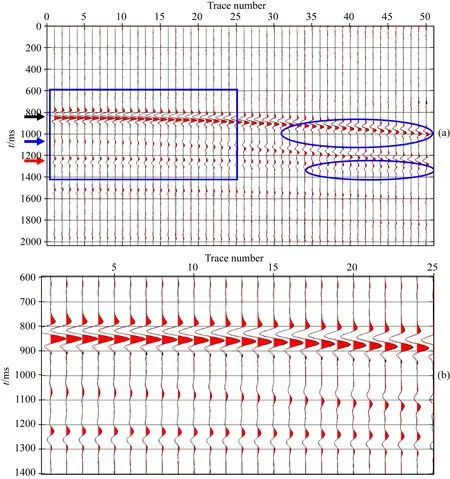
图10 X-Z平面的z分量合成剖面(a); (b) a图中蓝色矩形区域的放大视图Fig.10 The synthetic section (a) contains the z-component traces in the X-Z plane from both the LS scheme and the reflectivity method； (b) is an zoom-in view of the blue rectangular zone in (a)

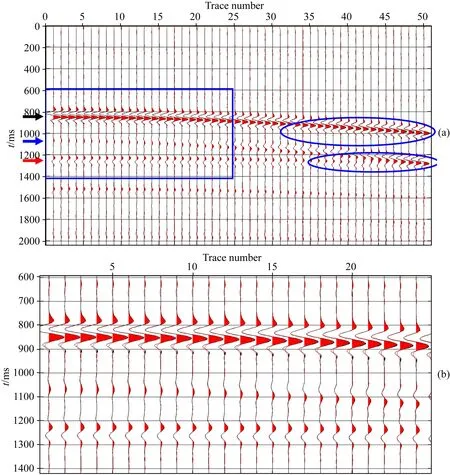
图11 Y-Z平面的z分量合成剖面(a)； (b) a图中蓝色矩形区域的放大视图Fig.11 The synthetic section (a) contains the z-component traces in the Y-Z plane from both the LS scheme and the reflectivity method； (b) is an zoom-in view of the blue rectangular zone in (a)

图10和图11中的黑色、蓝色和红色箭头分别指向第一界面反射的纵波、第一界面的PS转换波、第二界面的纵波.比较X-Z剖面和Y-Z剖面发现，在HTI介质层的顶部，反射纵波有一个显著的幅度差异，特别是在远偏移距处(大椭圆处)，揭示了在这两个不同的方位，纵波AVO响应的差异.为了看清HTI介质层顶部的全方位AVO(AVOA)响应，在所有检波器位置处，提取第一个纵波的最大振幅，然后绘制在图12.图中显示在400～600 m偏移距(入射角范围大约在25°～30°)范围内AVOA的椭圆变化，响应在水平面上，颜色表示振幅从0°到90°，颜色显示一个椭圆形的变化，Y轴表示裂缝走向.这表明，椭圆的长轴变化与裂缝走向一致.在图10和图11中，第一个纵波的传播时间相同，而第二个反射纵波在X-Z剖面(对应裂缝法向)的远距处(较小的蓝色椭圆区)传播时间稍大一些，这与裂缝法向纵波速度较小的事实相吻合.

LS正演模拟结果与反射率法模拟结果的定性比较如图10和图11所示.为了定量地检查结果，从图11a中的z分量中提取了20道(LS和反射率法结果的第11道到第30道).我们计算了这两种情况之间的相关系数，图13显示了对比结果，与0.97以上的相关系数有很高的相关性.两种方法依然存在差别，除了算法的差别外，部分原因是因为在震源的实现时，LS中震源的添加是在震源点附近的若干个网格点都施加了应力，和反射率法在一点施加震源有区别.

图12 HTI层顶部的纵波方位角AVO响应Fig.12 P-wave azimuthal AVO response at the top of the HTI layer

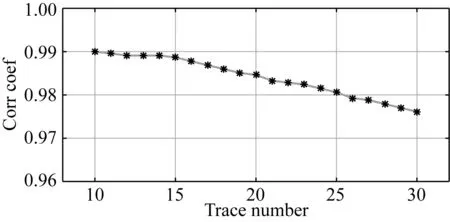
图13 从图11a中提取的20道地震记录中观察到两种方法的高相关系数Fig.13 High correlation coefficients are observed between the 20 extracted traces from figure 11a

5 结论

地震正演模拟是研究裂缝介质地震响应的重要方式.本文比较了三种不同类型的交错网格在复杂裂缝介质中模拟时的优点和局限，数值结果表明：SSG方法适用于简单各向异性裂缝介质(各向同性、VTI、HTI和正交各向异性)，对于复杂各向异性介质(单斜、TTI和三斜介质)，LS方法优于RSG方法，虽然菱形网格特性在数值实现中带来了不便，但可以通过本文提出的改进方法加以克服.改进后的方法极大简化了LS的实现，为开发基于正演模拟的复杂各向异性介质的方法提供了新的思路，有利于TTI、单斜和三斜介质中的RTM和FWI等基于交错网格的数据处理方法的应用.同时，对于大规模的复杂三维模型，本文提出了一种优化的模拟计算流程，将介质参数分解为介质构造参数和介质弹性参数，可以节约内存消耗并提高计算效率.三维LS正演模拟实例与反射率法的结果具有很好的一致性，验证了提出的三维LS方法的正确性.三维LS模拟工具为研究三维裂缝介质中地震波传播的各种波现象提供了一种新的实用手段.

致谢感谢审稿专家们和编辑们的宝贵意见.