层状各向异性地层中含环状天线槽随钻方位电磁波测井几何因子算法
2023-03-16于蕾汪宏年王浩森殷长春
于蕾, 汪宏年*, 王浩森, 殷长春
1 吉林大学物理学院计算方法与软件国际中心,长春 130012 2 河北建筑工程学院,河北张家口 075000 3 吉林大学地球探测科学与技术学院,长春 130026
0 引言
经过近40年的发展,随钻测井已成为智能导钻、地质导向、复杂储层综合评价等的重要工具,在整个油气层勘探开发中发挥着越来越重要的作用.目前,各大石油服务公司相继研究开发出多种不同结构的随钻方位电磁波测井技术,例如,斯伦贝谢(Schlumberger)公司的PeriScope15(Li et al., 2005;Omeragic et al., 2005)、贝克休斯(Baker Hughes)公司的AziTrak(Bell et al., 2006;Wang et al., 2006,2007;Kennedy et al., 2009;Fang, 2011)、哈里伯顿(Halliburton)公司的ADR(Bittar et al., 2009)、威德福(Weatherford)公司的GuideWave(Li et al., 2014)以及中国科学院地质与地球物理研究所自主研发的正交随钻方位仪器(汪宏年等, 2021;于蕾等, 2021;Yu et al., 2022)等.这些仪器普遍采用多频多源距的轴向、倾斜或共面(横向)(Hong et al., 2022)发射与接收天线系统,通过测量多分量磁场信息,实现复杂储层条件下精确地质导向.为了提高仪器测量效率和精度,实际随钻电阻率测井仪器的发射与接收天线均安装在刻槽钻铤的天线槽中(Clark et al., 1990),并利用铁氧体等磁性材料和玻璃钢等高阻耐磨性材料对线圈进行封存,以避免线圈与井眼泥浆直接接触,提高仪器的耐用性(Park and Eom, 1999;Shumpert and Butler, 1998).在仪器优化设计和资料处理过程中,研究建立一套复杂地层条件下含有天线槽的随钻方位电磁测井响应数值模拟方法是一项非常重要的工作.需要指出的是这种含有天线槽的随钻方位电磁响应的数值模拟往往是十分复杂的,且计算工作量也非常大.目前,半解析算法(汪宏年等, 2021)以及三维数值模拟算法(于蕾等, 2021;Yu et al., 2022;许巍等, 2016;Wang and Signorelli, 2004)等均已得到广泛研究和应用.在此基础上,本文将基于感应测井中的几何因子理论,建立一套确定各向异性地层中随钻方位电磁波仪器纵横向探测能力的新算法,用于快速分析评价复杂地层条件下仪器的探测性能.
早在20世纪40年代,Doll首先提出了几何因子理论(Doll, 1949),将接收线圈上的感应电动势表示为地层中所有感应电流环产生的感应电动势的叠加.在此基础上,Duesterhoeft等(Duesterhoeft, 1961;Duesterhoeft et al., 1961;Moran and Kunz, 1962)借助均匀介质中电磁场解析解对Doll几何因子进行改进给出了传播几何因子,在石油工业中也被称为趋肤效应几何因子(田子立等, 1984).此后,基于摄动原理又陆续发展了几何因子的几种不同推导与物理解释,并在感应测井资料处理中得到广泛应用(Anderson and Gianzero, 1982;Moran, 1982;张庚骥, 1982;Howard et al., 1990).Fang等将Moran几何因子推广到了斜井问题中(Fang et al., 1999).针对高频电磁波测井,Zhou(Hiliker et al., 1992)和Zhou和邢光龙等(Hiliker et al.,1992;邢光龙和杨德善,2004)进一步将几何因子理论推广应用于幅度比与相位差对介电常数、电导率响应函数研究中.针对新的多分量感应测井问题,Alumbaugh和王磊等分别研究了各向同性和各向异性多分量仪器响应的几何因子算法(Alumbaugh and Lu, 2001;Alumbaugh and Wilt, 2001;Barber et al., 2004;王磊等, 2015;邓少贵等, 2020).需要指出的是,到目前为止,借助几何因子理论分析测井响应的研究工作几乎都是针对均匀介质,即使包含异常体结构或斜井时亦是基于均匀介质进行差分或Born近似,且在几何因子计算过程中往往忽略了钻铤以及收发线圈的真实几何结构,对于含有金属钻铤和环状天线槽的几何因子仍然缺少系统研究.基于摄动原理和模式匹配(NMM)算法对刻槽钻铤上随钻电磁几何因子的研究已取得了初步进展(汪宏年等, 2021),但对于层状各向异性地层中倾斜井眼情况下含天线槽的随钻方位电磁波测井完整几何因子(即轴向分量和交叉分量几何因子)的研究仍然是空白.
本文将针对含有天线槽的随钻方位电磁波测井仪器,借助摄动原理和一阶Born 近似理论,建立各向异性非均质地层中随钻方位电磁波测井空间灵敏度函数(三维几何因子)以及各分量径向、纵向微分几何因子的有效算法.算法的关键是利用柱坐标系下耦合势Helmholtz方程三维有限体积法(3-D FVM)(张烨等, 2012;Wang et al., 2020;陈博等, 2021;于蕾等, 2021;Yu et al., 2022)同时确定电流源和磁偶极子源的电磁场Green函数的数值解,并应用摄动原理和Green第二积分公式建立电导率相对摄动与电磁场微小变化量之间的关系,从而得到不同分量空间灵敏度函数表达式.并将其在径向(垂直仪器轴方向)或纵向(沿仪器轴方向)上的数值积分作为各分量的微分几何因子,用于分析考查非均质各向异性地层中不同工作频率、不同相对倾角情况下随钻方位电磁波测井仪器的纵横向探测能力,为仪器设计、实际测量以及资料处理提供理论参考.
1 基本理论
1.1 电导率摄动与一阶Born近似情况下的电磁场
图1a是随钻方位电磁波测井仪器结构示意图,其中,Tz1/Tz2(Tz3/Tz4)分别是长(短)源距轴向发射线圈,Rz1/Rz2和Rx1/Rx2分别是轴向和横向接收线圈.所有线圈均安装在环状天线槽中的铁氧体与玻璃钢之间(见图1(b,c)).仪器参数、钻铤以及环状天线槽的尺寸见文献(汪宏年等, 2021;于蕾等, 2021;Yu et al., 2022).引入仪器柱坐标系Oρφz并保证其z轴与钻铤中轴线一致,这时随钻方位电磁波测井正演模拟可以表示为求解如下的Maxwell方程(时间变化关系为e-iω t)
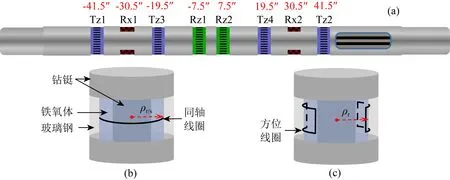
图1 随钻方位电磁波测井仪器结构示意图(a) 刻槽钻铤结构与收发线圈分布;(b) 天线槽中的轴向线圈;(c) 天线槽中的横向线圈.Fig.1 The downhole structure of the LWD azimuthal electromagnetic wave tool(a) Grooved drill collar and distribution of transmitting and receiving coils; (b) Coaxial coils in the antenna recesses;(c) Transverse coils in the antenna recesses.
(1)
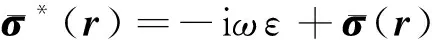
仪器柱坐标系中电导率张量为
(2)
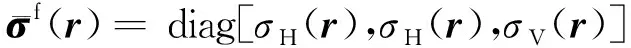
当水平和垂直电导率产生微小摄动δσH(r)和δσV(r)时,利用微分公式从方程(2)可以得到仪器柱坐标系中电导率的相对摄动量(陈博等, 2021;汪宏年等, 2021)
(3)
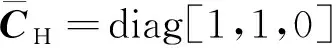
由摄动原理以及电导率相对摄动量(3),从方程(1)可以推导出电导率摄动与电场和磁场微小变化量δE(r;rs,i)和δH(r;rs,i)间的线性关系(即摄动方程)
(4)
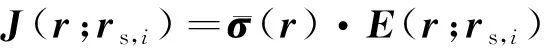
在接收线圈Rz1和Rz2所在位置rz,j=(ρr,zr,j),(j=1,2)处引入环状电流源电场和磁场Green函数EJφ(r;rz,j)和HJφ(r;rz,j)
(5)
其中,上角标Jφ表示是由单位环状电流源产生的电磁场.方程(5)与方程(1)除源的位置不同外,其他部分完全相同.
利用Green第二积分公式与互易原理将方程(4)和(5)结合,得到轴向接收线圈Rz1/Rz2上电场强度Eφ分量微小变化与电导率摄动间的线性关系(陈博等, 2021)
J(r;rs,i)dr.
(6)
与轴向接收线圈不同,横向接收线圈Rx1和Rx2内部介质是均匀的且其尺寸往往很小,其感应电动势可以根据磁通量对时间的变化率计算.为确定电导率微小摄动对横向接收线圈上感应电动势的影响,仅需要研究接收线圈中心位置径向磁场强度的变化量,为此,分别在Rx1和Rx2的中心位置rx,k=(ρr,φr,zx,k),(k=1,2)处引入径向磁偶极子源电磁场Green函数EMρ(r;rx,k)和HMρ(r;rx,k)
(7)
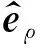
这时,利用Green第二积分公式与互易原理并将方程(4)和(7)结合,可以得到横向接收线圈Rx1/Rx2上径向磁场强度微小变化量δHρ与电导率摄动间的线性关系:
·J(r;rs,i)dr.
(8)
1.2 各向异性地层中的空间灵敏度函数(或三维几何因子)
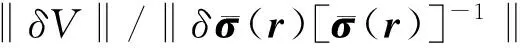
1.2.1 幅度比和相位差的空间灵敏度函数(或三维几何因子)
随钻方位电磁波测井仪器轴向分量输出信号往往是两个轴向接收线圈上感应电动势的比值,并用其振幅和相位即幅度比和相位差表示(王浩森等, 2016;汪宏年等, 2021),例如,长源距幅度比(分贝)和相位差计算公式分别为
(9)
其中,Vzz(rz,1;rs,1)和Vzz(rz,2;rs,1)分别是发射线圈Tz1在轴向接收线圈Rz1和Rz2上的感应电动势,Re和Im分别表示取复数的实部和虚部.利用复合函数求导法则与全微分公式对方程(9)进行处理,得到幅度比和相位差变化量δAtt1和δPS1与两个轴向接收线圈上感应电动势变化量δVzz(rz,1;rs,1)和δVzz(rz,2;rs,1)间的关系
(10)
进而,可得到幅度比和相位差变化量与电导率相对摄动量间的关系
(11)

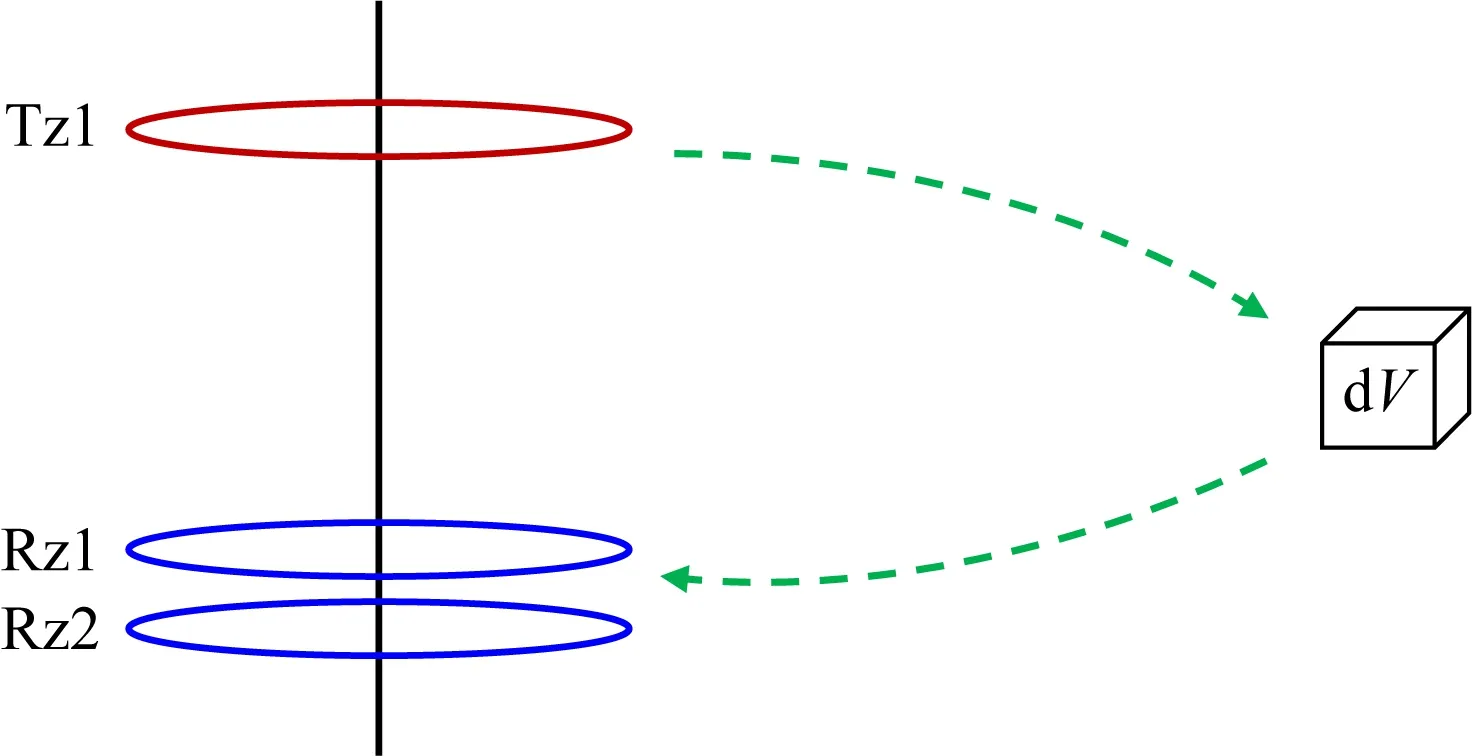
图2 空间灵敏度函数理论解释示意图Fig.2 Theoretical explanation of spatial sensitivity function
(12)
其中,Szz,H(r;rz,j;rs,i)和Szz,V(r;rz,j;rs,i)为轴向感应电动势对于水平电导率和垂直电导率的空间灵敏度函数(见附录A).
1.2.2 交叉分量的空间灵敏度函数(或三维几何因子)
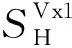
(13)
以及交叉分量Vx1的变化量与水平和垂直电导率相对摄动量间的关系
(14)
其中,Sxz,H(r;rx,k;rs,i)和Sxz,V(r;rx,k;rs,i)分别为横向感应电动势对于水平和垂直电导率的空间灵敏度函数(或三维几何因子)(见附录A);L表示各线圈到仪器中心的距离(见图1).采用同样方法也可以推导出横向接收线圈输出量Vx2的空间灵敏度函数表达式(略).
1.3 各向异性地层中的微分几何因子
空间灵敏度函数(三维几何因子)可以应用于研究分析地层中不同位置的单位体积元上水平和垂直电导率相对摄动对测量结果产生的影响.将空间灵敏度函数沿纵向和径向分别积分可以获得径向微分几何因子和纵向微分几何因子,能够更好地用于分析考查仪器探测深度和纵向分辨率.
1.3.1 幅度比和相位差的微分几何因子
对方程(12)中的空间灵敏度函数沿纵向积分,得
(15)
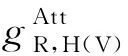
(16)
同样地,对方程(12)中的空间灵敏度函数沿径向积分,得
(17)
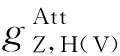
(18)
1.3.2 交叉分量的微分几何因子
类似地,对方程(14)中的空间灵敏度函数进行积分,则可以得到交叉分量Vx1相对于水平和垂直电导率的径向和纵向微分几何因子
(19)
以及总径向和总纵向微分几何因子
(20)
其物理含义与前面的幅度比和相位差的纵向(径向)微分几何因子相同.
随钻方位电磁波仪器采用完全对称的测量方式,通过上下对称的测量结果加以平均得到所谓的补偿信号,以便于降低井眼和层界面影响.为此,对于上面的各个发射天线对应的空间灵敏度函数与微分几何因子,分别对上下对称的相关计算结果加以平均就得到补偿空间灵敏度函数与补偿微分几何因子(见附录B).
1.4 环状电流源和磁偶极子源电磁场的三维有限体积法(3-D FVM)正演
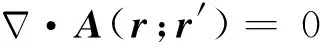
(21)
方程(21)中右端项分别对应如下三种不同情况:
当α=1时,对应方程(1)的右端项,即
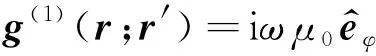
(22)
这时方程(21)表示四个轴向发射线圈产生的电磁场耦合势,且r′=rs,i对应于四个轴向发射线圈的位置;
α=2时,对应方程(5)的右端项
(23)
这时方程(21)代表轴向接收线圈位置上单位电流产生的电磁场耦合势,并且r′=rz,j对应两个轴向接收线圈位置;而α=3的右端项为
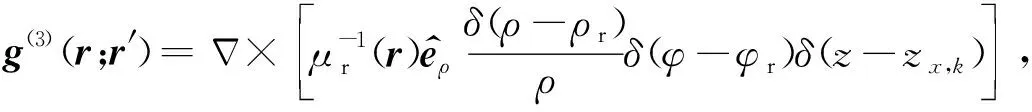
k=1,2,
(24)
其对应于方程(7),即横向接收线圈位置上单位径向磁偶极子产生的电磁场耦合势,并且r′=rx,k对应两个横向接收线圈的位置.
应用文献(于蕾等, 2021;Yu et al., 2022)中的不规则Yee交错网格对含有天线槽的金属钻铤周围的求解区域进行网格剖分,并按照3-D FVM对方程(21)—(24)进行离散,则得到关于未知矢势和标势的大型代数方程为
FXα=bα,
(25)
其中,F为N×N阶非对称的稀疏系数矩阵,是方程(21)左端的离散结果,只与地层参数有关;Xα=(Aρ,Aφ,Az,φ)T为各个剖分网格交错节点上未知耦合势组成的N维向量;bα是方程(21)右端项的离散结果,对应(22)—(24)的离散向量.
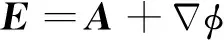
2 数值结果
根据上述算法,本节将针对钻铤上含环状天线槽的仪器模型,给出均匀各向同性、均匀各向异性以及包含水平层界面地层中空间灵敏度函数(三维几何因子)、径向和纵向微分几何因子的数值结果,并对轴向响应数值结果进行归一化处理,考查随钻方位电磁波测井仪器的探测特征.此外,为减少论文篇幅以及根据数值结果的对称性,本论文仅给出补偿空间灵敏度函数、补偿径向和补偿纵向微分几何因子的数值结果,同时由于随钻方位电磁波仪器受井眼泥浆影响较小,数值计算过程中忽略井眼影响.
2.1 各向同性均匀地层中幅度比和相位差的几何因子
首先,针对σH=σV=0.1 S·m-1的均匀各向同性地层,利用数值模式匹配(NMM)算法(汪宏年等, 2021)与本文3-D FVM得到的几何因子计算结果进行对比,检验算法的有效性.
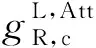
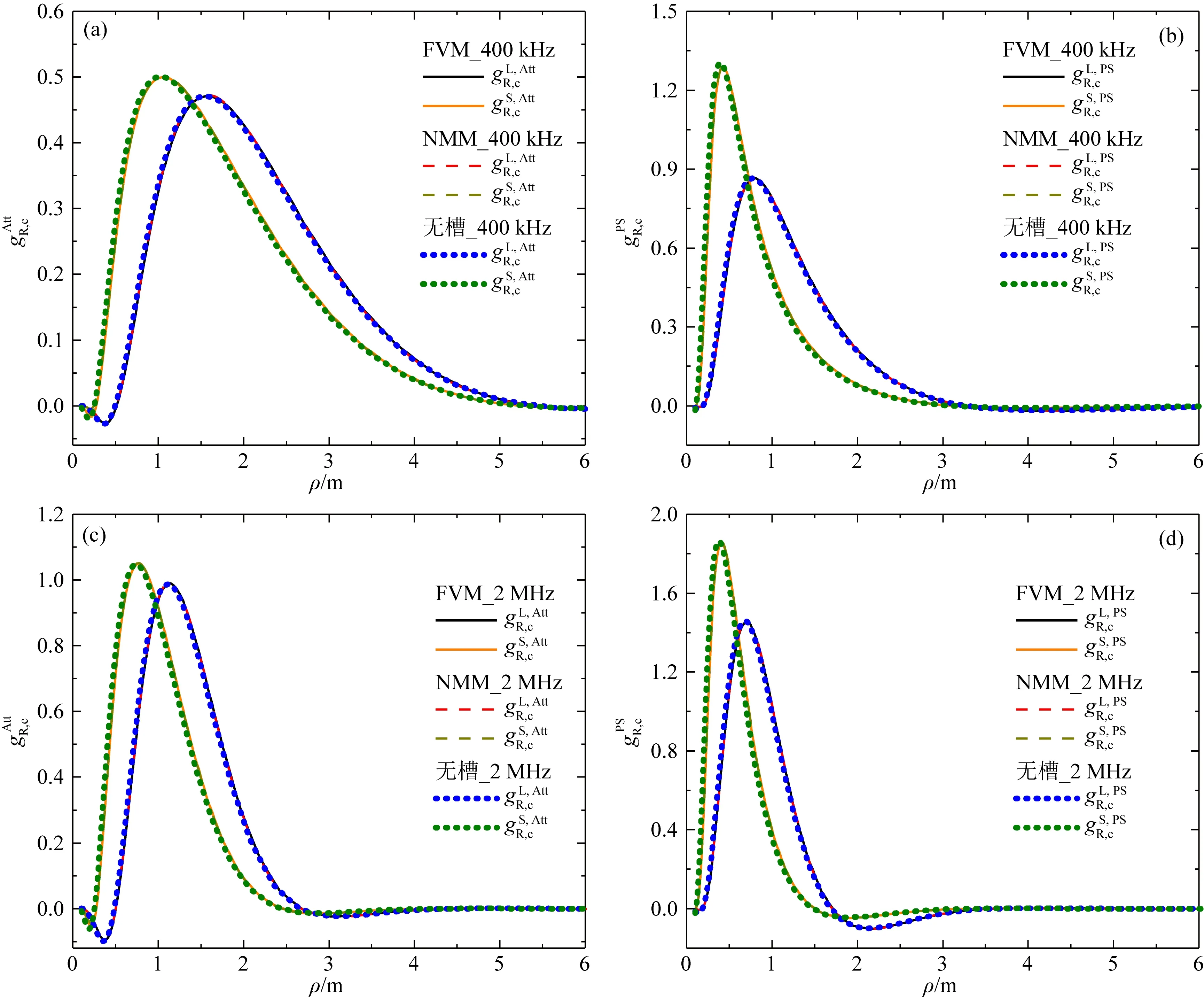
图3 各向同性均匀地层中3-D FVM与NMM算法得到的幅度比和相位差总径向微分几何因子对比(a) 低频幅度比; (b) 低频相位差; (c) 高频幅度比; (d) 高频相位差.Fig.3 Comparison of total radial differential geometrical factors of Att and PS obtained by 3-D FVM and NMM in isotropic homogeneous formation
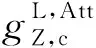
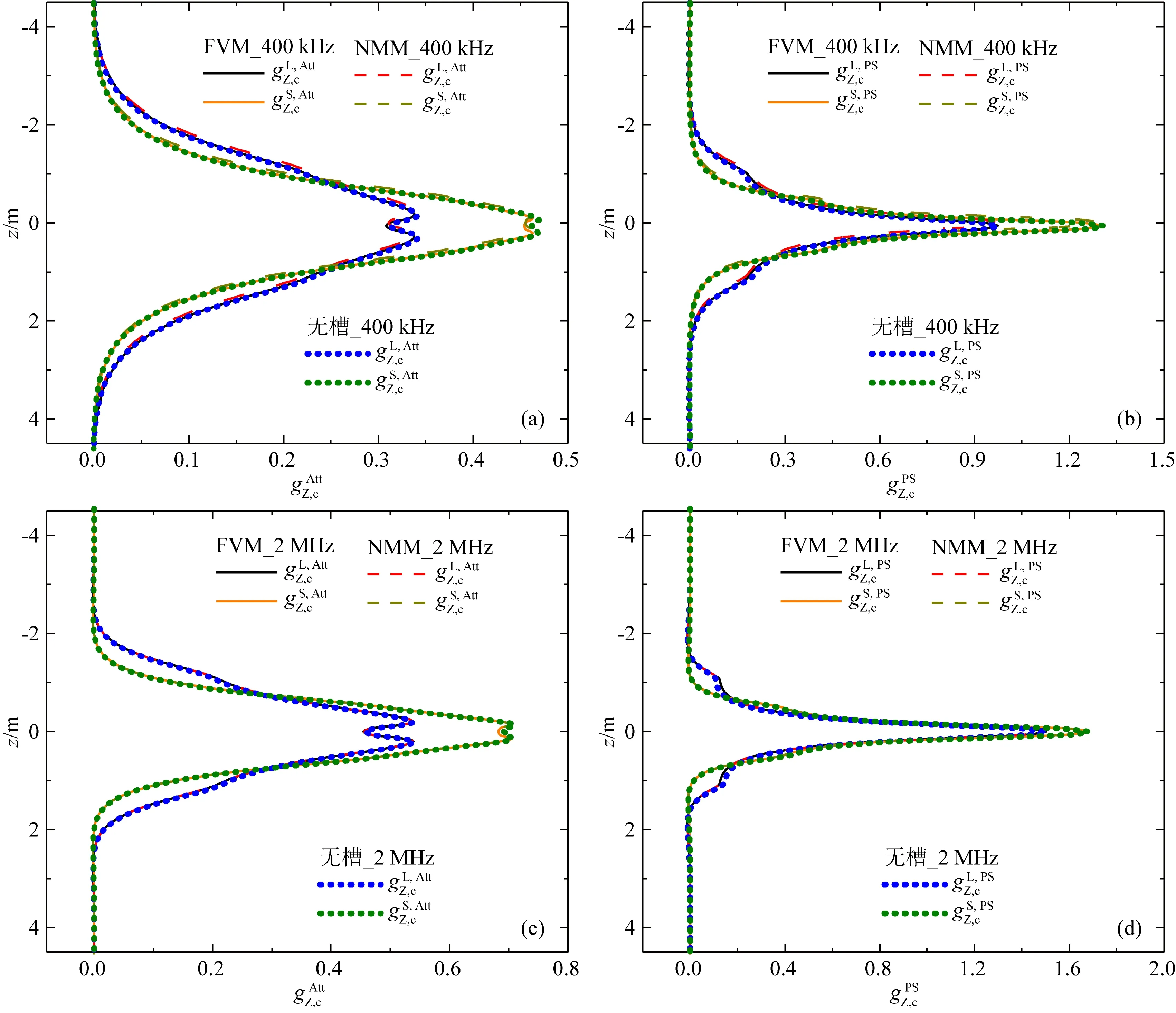
图4 各向同性均匀地层中3-D FVM与NMM算法得到的幅度比和相位差总纵向微分几何因子对比(a) 低频幅度比; (b) 低频相位差; (c) 高频幅度比; (d) 高频相位差.Fig.4 Comparison of total vertical differential geometrical factors of Att and PS obtained by 3-D FVM and NMM in isotropic homogeneous formation
此外,图3和图4中也同时给出光滑钻铤上无天线槽时(线圈缠绕在钻铤表面)的结果,此结果也由3-D FVM计算得到.结果显示无天线槽与含天线槽时的微分几何因子几乎重合,正如文献(汪宏年等, 2021)中所说,天线槽中铁氧体有效地提高了发射线圈的发射功率和接收信号强度,但对钻铤外电磁场空间分布的影响较小,幅度比和相位差依然主要反映地层电导率的变化特征.
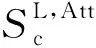
2.2 均匀TI地层中不同仪器倾角时幅度比和相位差的几何因子
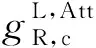
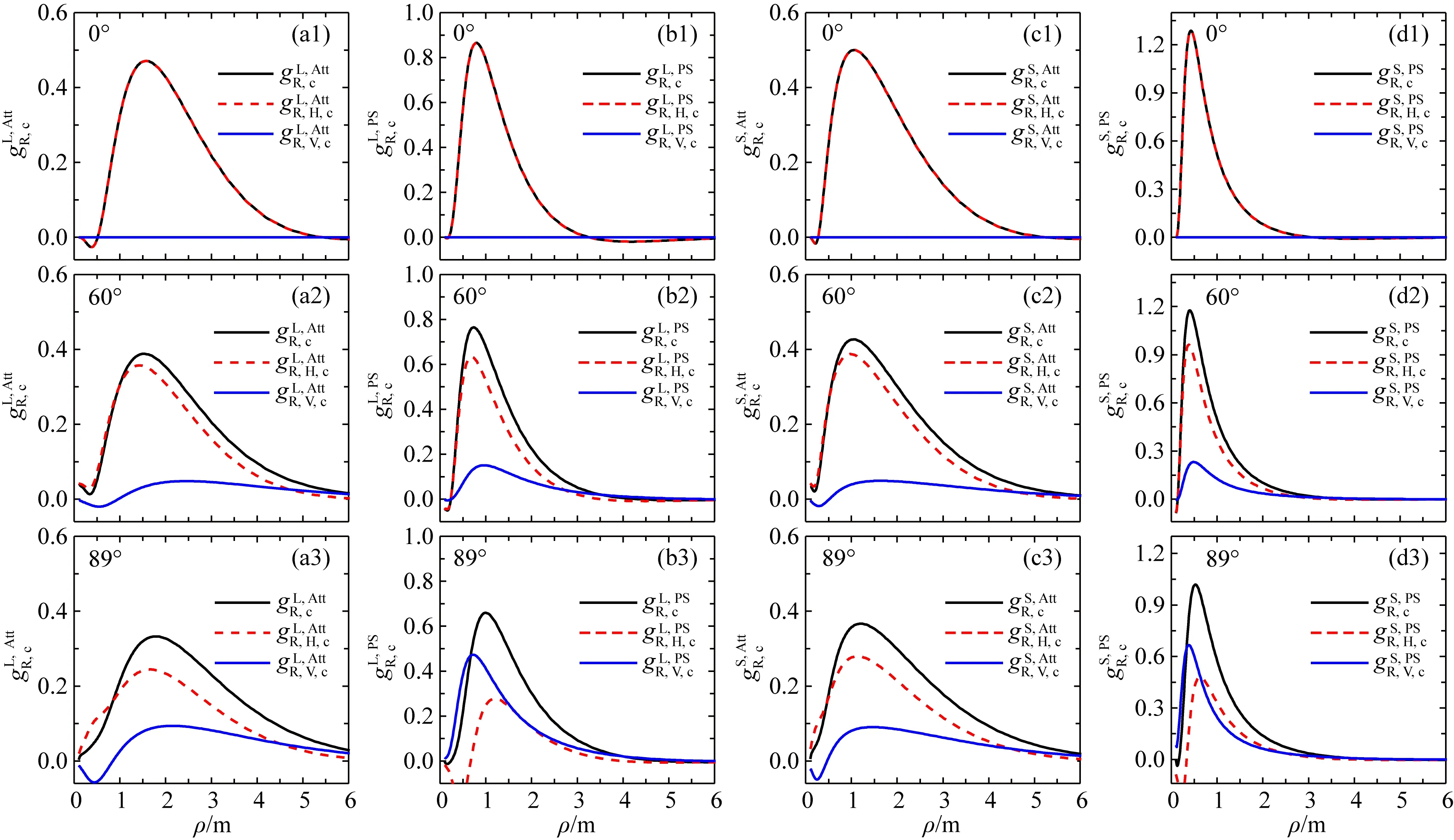
图6 均匀TI地层中倾角为0°、60°和89°时长短源距幅度比和相位差的总径向微分几何因子以及与水平和垂直电导率关联的径向微分几何因子(f=400 kHz)(a1—a3) 长源距幅度比; (b1—b3) 长源距相位差; (c1—c3) 短源距幅度比; (d1—d3) 短源距相位差.Fig.6 Radial differential geometrical factors of Att and PS to total conductivity, horizontal, and vertical conductivity in homogeneous TI formations with dips of 0, 60 and 89 degrees (f=400 kHz)(a1—a3) Att of long spacing; (b1—b3) PS of long spacing; (c1—c3) Att of short spacing; (d1—d3) PS of short spacing.
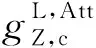
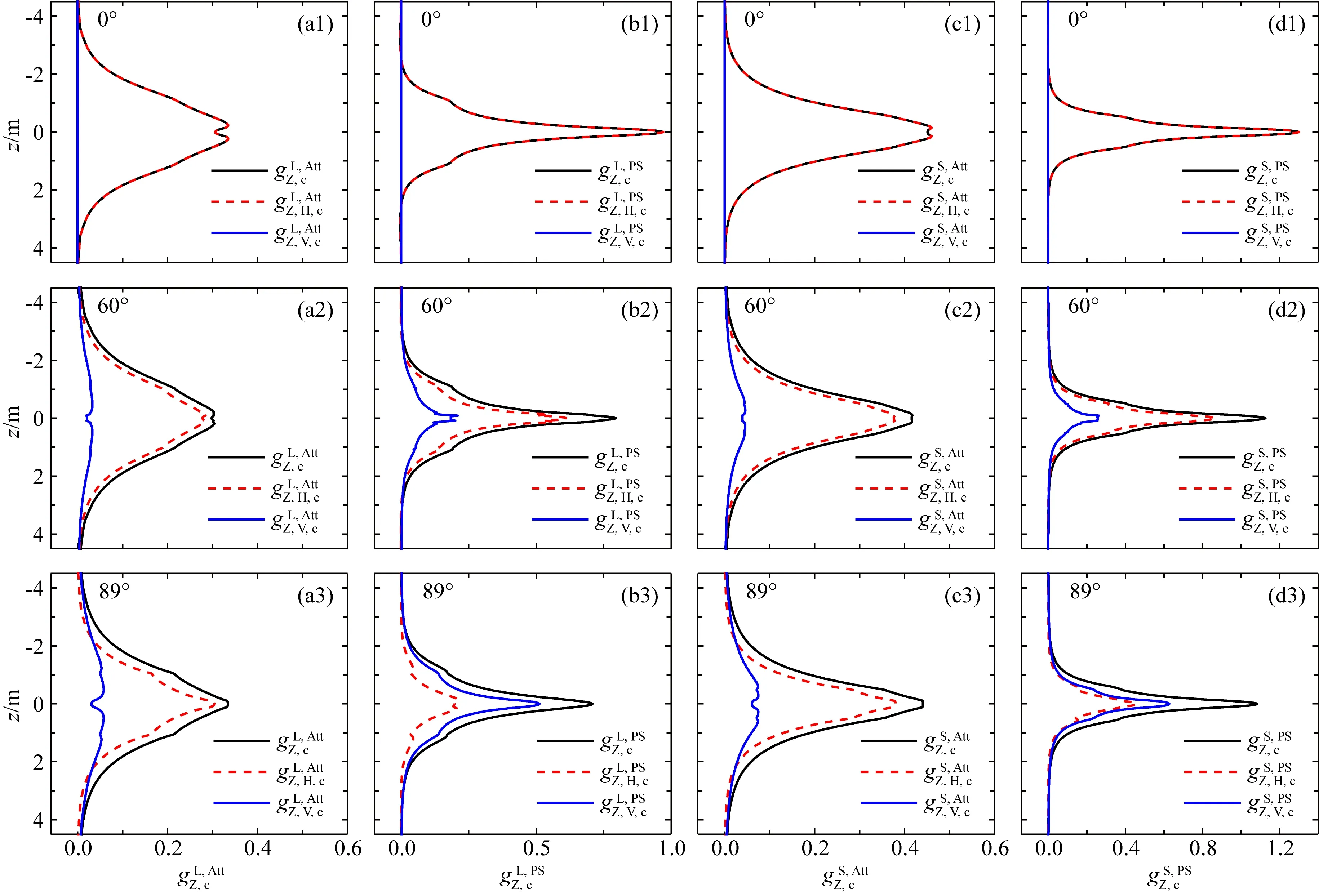
图7 均匀TI地层中倾角为0°、60°和89°时长短源距幅度比和相位差的总纵向微分几何因子以及与水平和垂直电导率关联的纵向微分几何因子(f=400 kHz)(a1—a3) 长源距幅度比; (b1—b3) 长源距相位差; (c1—c3) 短源距幅度比; (d1—d3) 短源距相位差.Fig.7 Vertical differential geometrical factors of Att and PS to total conductivity, horizontal, and vertical conductivity in homogeneous TI formations with dips of 0, 60 and 89 degrees (f=400 kHz)(a1—a3) Att of long spacing; (b1—b3) PS of long spacing; (c1—c3) Att of short spacing; (d1—d3) PS of short spacing.
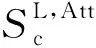
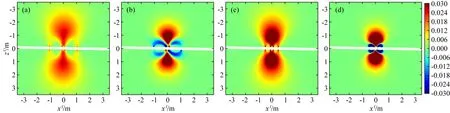
图8 均匀TI地层中倾角为89°时长短源距幅度比和相位差总空间灵敏度分布(y=0和f=400 kHz)(a) 长源距幅度比; (b) 长源距相位差; (c) 短源距幅度比; (d) 短源距相位差.Fig.8 Total spatial sensitivity of Att and PS in homogeneous TI formation at dip of 89 degree (y=0 and f=400 kHz)(a) for PS of short spacing.
2.3 两层模型中幅度比和相位差总空间灵敏度函数
为进一步研究考查轴向接收线圈Rz1/Rz2上幅度比和相位差总空间灵敏度函数的变化特征、分析仪器的探边能力,本节将分别给出各向同性和各向异性两层模型中,仪器位于两个不同位置时幅度比和相位差的总空间灵敏度.图9是两层地层模型示意图,其水平地层边界位置zb=0 m,而仪器位置分别为d=±1.0 m,且倾角固定为89°,为减少文章篇幅,这里仅给出低频情况下y=0的垂直截面xfOzf上总空间灵敏度.
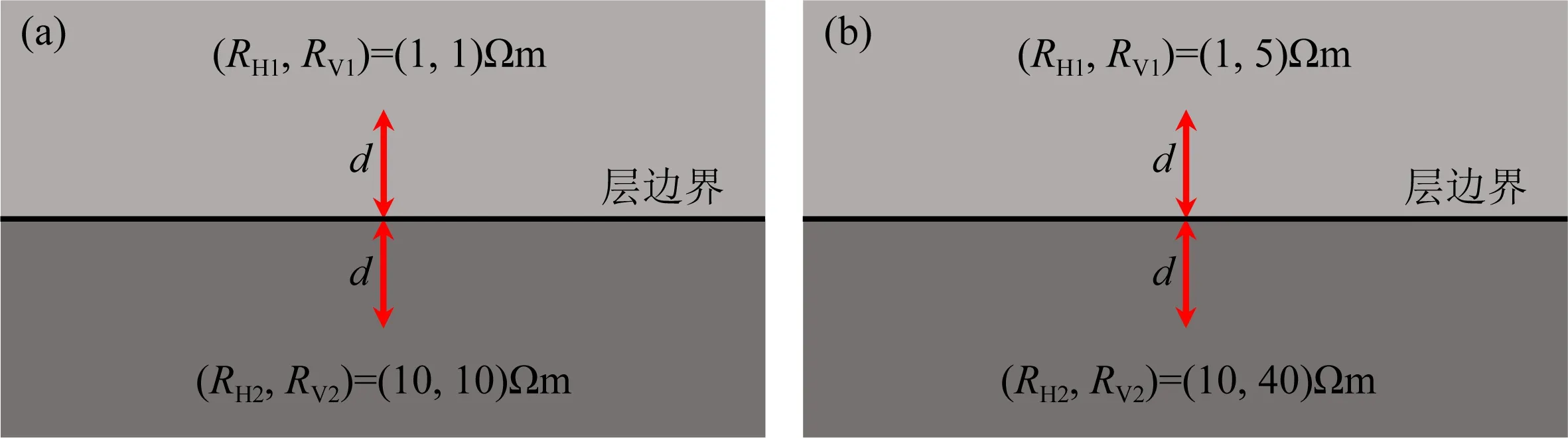
图9 两层地层模型示意图(a) 各向同性; (b) TI.Fig.9 Two-layer formation model(a) Isotropic; (b) TI.
2.3.1 两层各向同性地层模型
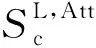
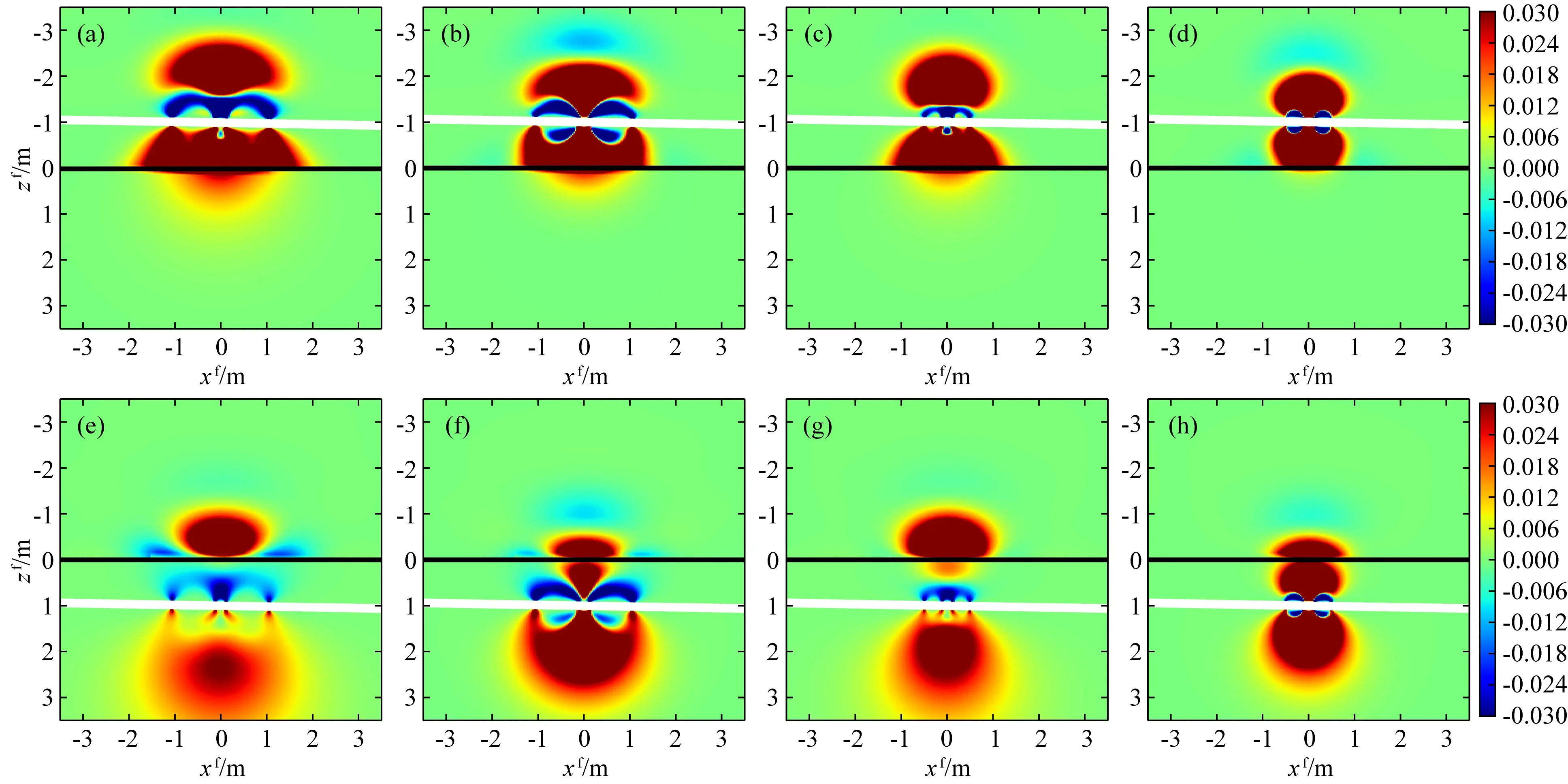
图10 两层各向同性地层中倾角为89°、测点d=±1.0 m时幅度比和相位差总空间灵敏度分布(y=0和f=400 kHz)(a) d=-1.0 m时; (b) d=-1.0 m时; (c) d=-1.0 m时; (d) d=-1.0 m时; (e) d=1.0 m时; (f) d=1.0 m时; (g) d=1.0 m时; (h) d=1.0 m时.Fig.10 Total spatial sensitivity of Att and PS in two-layer isotropic formation with dip of 89 degree and measuring position of d=±1.0 m (y=0 and f=400 kHz)
2.3.2 两层TI地层模型
图9b是两层TI模型,其水平电导率与图9a相同,而上下层垂直电导率分别为σV1=0.2 S·m-1和σV2=0.025 S·m-1.图11是仪器在该模型中分别位于d=-1.0 m和d=1.0 m时低频长(短)源距幅度比和相位差总空间灵敏度分布图.其中,图11(a—d)为d=-1.0 m时的总空间灵敏度,而图11(e—h)是d=1.0 m时的总空间灵敏度.对比图10中各向同性模型与图11中TI模型结果可以看出,地层电导率各向异性对空间灵敏度的影响很大,TI模型中仪器的探边能力减弱.但从图11仍然可以看出,当仪器位于上部低阻层(d=-1.0 m)时,地层边界与仪器之间区域的空间灵敏度是明显增强的,且在高阻层中灵敏度快速减小.而当仪器位于下部高阻层(d=1.0 m)时,在仪器与层边界之间的高阻区域中空间灵敏度值明显变小,仪器在高阻地层时具有更强的探边能力.
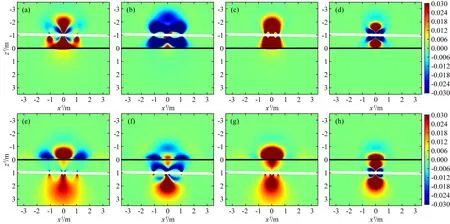
图11 两层TI模型中倾角为89°、测点d=±1.0 m时幅度比和相位差总空间灵敏度分布(y=0和f=400 kHz)(a) d=-1.0 m时; (b) d=-1.0 m时;(c) d=-1.0 m时; (d) d=-1.0 m时;(e) d=1.0 m时; (f) d=1.0 m时;(g) d=1.0 m时; (h) d=1.0 m时.Fig.11 Total spatial sensitivity of Att and PS in two-layer TI formation with dip of 89 degree and measuring position of d=±1.0 m (y=0 and f=400 kHz)
2.4 均匀地层中交叉分量总空间灵敏度函数
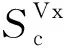
图12是均匀各向同性和均匀TI地层中交叉分量空间灵敏度分布图,其中,图12(a,b)是电导率为0.1 S·m-1的各向同性地层中的数值结果,而图12(c,d)是水平电导率为σH=0.1 S·m-1、各向异性系数为λ=2的TI地层中的结果.与幅度比和相位差不同,交叉分量总空间灵敏度在空间上呈正负相间分布,特别是对图12(a,b)中数值结果进行积分时发现,各向同性地层中的空间灵敏度的体积分等于零,说明在各向同性均匀地层中交叉分量对地层电导率变化不敏感,实际正演结果值始终等于零.而图12(c,d)的均匀TI地层中空间灵敏度虽然也呈正负相间分布,但对其进行积分并不等于零,因此,在均匀地层倾斜井眼中,根据交叉分量是否等于零能够判断出地层电导率是否存在各向异性.
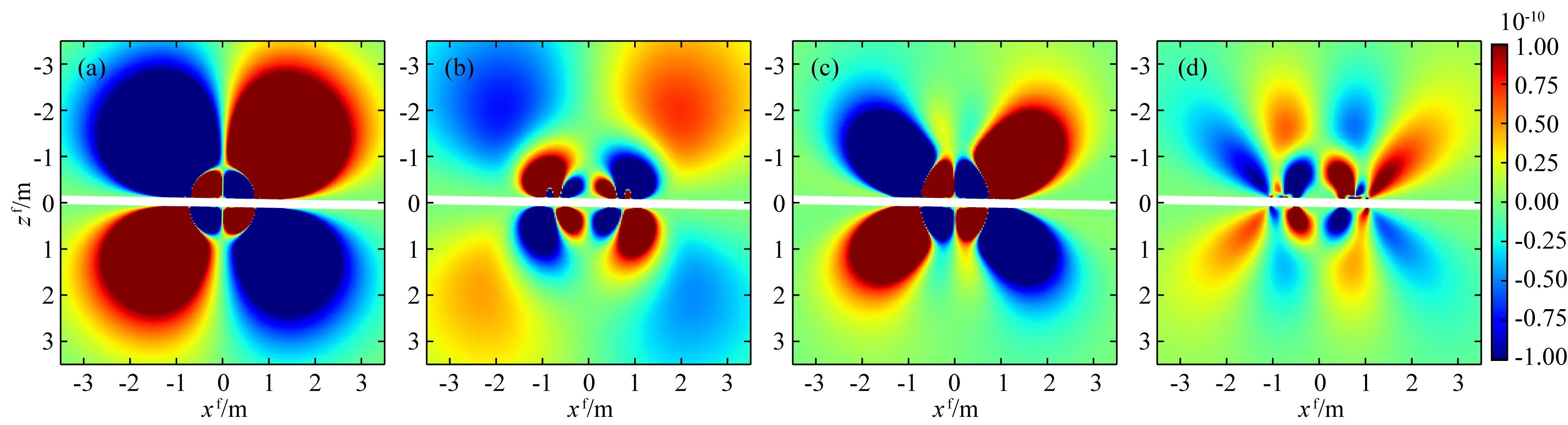
图12 均匀各向同性与TI地层中倾角为89°时交叉分量实部和虚部总空间灵敏度分布(y=0和f=400 kHz)(a) 各向同性Re[]; (b) 各向同性Im[]; (c) TI地层中Re[]; (d) TI地层中Im[].Fig.12 Total spatial sensitivity of real and imaginary parts of cross-components in both isotropic and TI homogeneous formation with dip of 89 degree (y=0和f=400 kHz)
2.5 两层模型中交叉分量总空间灵敏度函数
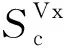
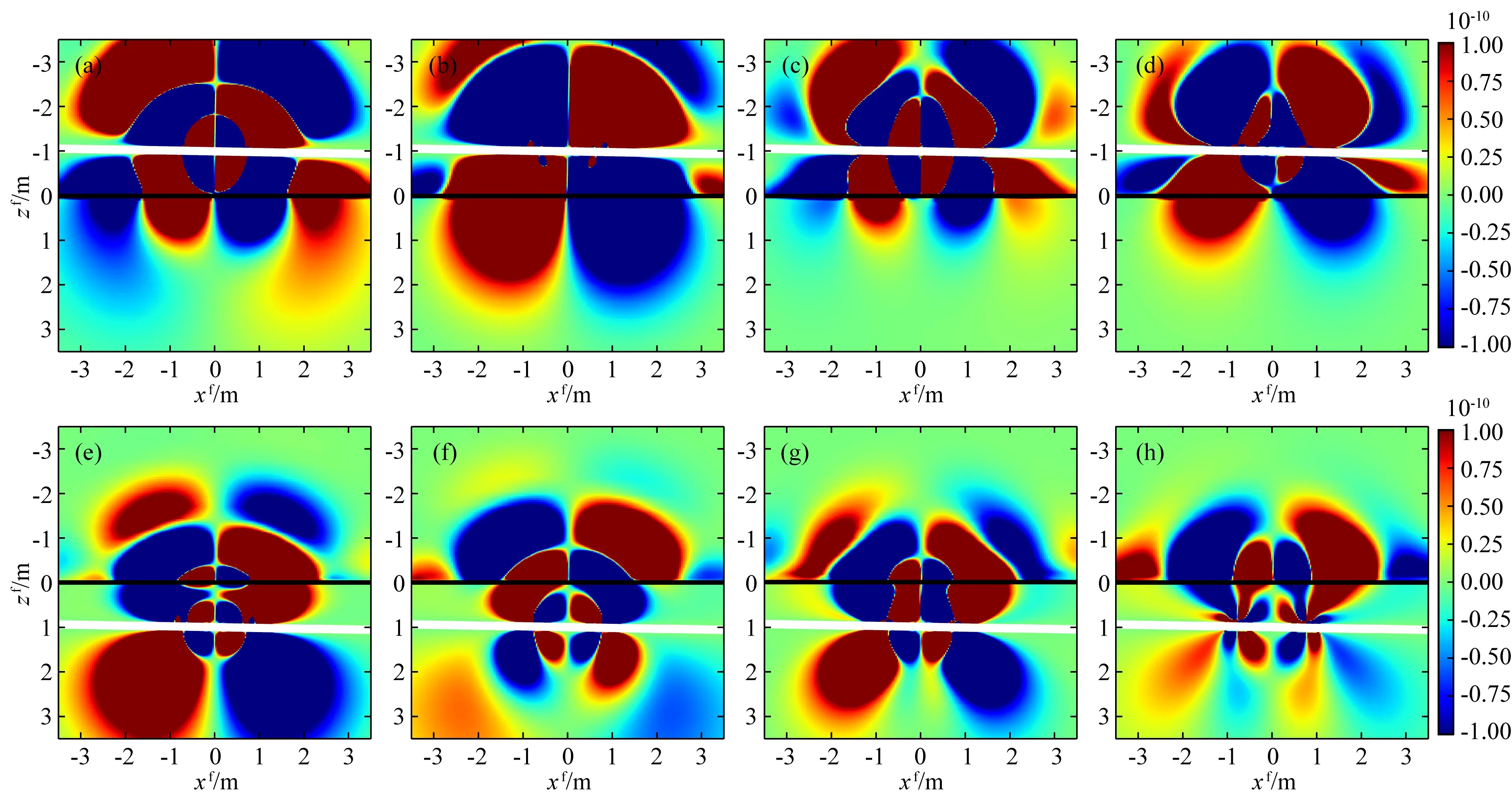
图13 两层各向同性与TI地层中倾角为89°、测点d=±1.0 m时交叉分量实部和虚部总空间灵敏度分布(y=0和f=400 kHz)(a)和(b)各向同性地层中d=-1.0 m时Re[]和Im[];(c)和(d)TI地层中d=-1.0 m时Re[]和Im[];(e)和(f)各向同性地层中d=1.0 m时Re[]和Im[]; (g)和(h)TI地层中d=1.0 m时Re[]和Im[].Fig.13 Total spatial sensitivity of real and imaginary parts of cross-components in both isotropic and TI two-layer formation with dip of 89 degree and measuring position of d=±1.0m (y=0和f=400 kHz)(a) and (b) in TI formation at d=-1.0 m;(e) and (f) in TI formation at d=1.0 m.
3 结论
本文针对中国科学院地质与地球物理研究所自主研发的新型随钻方位电磁波测井仪器,基于感应测井中的几何因子理论与一阶Born 近似理论,结合柱坐标系下耦合势Helmholtz方程三维有限体积算法,提出了一种各向异性非均匀地层中随钻方位电磁波测井仪器的空间灵敏度函数以及各个分量的径向和纵向微分几何因子算法.数值结果模拟考查了不同频率、仪器倾角条件下,各向同性、各向异性以及纵向成层地层中的几何因子,分析考查了仪器的探测特性和探边能力.
数值结果表明:(1)频率越低、源距越长,线圈的径向探测深度越大,幅度比比相位差具有更大的探测深度;相反的,频率越高、源距越短,线圈的纵向分辨能力越强,相位差比幅度比纵向分辨力强;(2)均匀各向异性地层中,仪器倾角越大,与垂直电导率关联的微分几何因子越大,与水平电导率关联的微分几何因子越小;在大倾角的井眼中,相位差曲线更能够反应出地层垂直电导率的变化;(3)两层模型中,测点位置距离层边界较近时,空间灵敏度分布在层边界处明显分层;仪器在高阻地层时具有更强的探边能力;交叉分量的探边能力好于幅度比和相位差.
附录A
轴向感应电动势的空间灵敏度函数(或三维几何因子):
从方程(6)不难看出轴向接收线圈Rz1/Rz2上感应电场强度的变化量与方位角无关,所以其感应电动势变化量可以表示为δVzz(rz,j;rs,i)=2πρrδEφ(rz,j;rs,i).
将方程(3)代入(6)并经适当整理,得到轴向接收线圈上感应电动势微小变化量与地层水平和垂直电导率相对摄动间的关系
(A1)
其中,bm表示钻铤外半径,而右端项被积函数中Szz,H和Szz,V表达式为
(A2)
其中,上角标f表示地层坐标系.该表达式称为轴向感应电动势对于水平电导率(或垂直电导率)的空间灵敏度函数(或三维几何因子).
横向感应电动势的空间灵敏度函数(或三维几何因子):
横向接收线圈Rx1/Rx2上的感应电动势变化量为δVxz(rx,k;rs,i)=iωμSxδHρ(rx,k;rs,i),其中Sx是横向接收线圈的面积.
将(3)代入式(8)中,得到发射线圈(Tz1/Tz2和Tz3/Tz4)在横向接收线圈Rx1/Rx2上感应电动势的变化量与水平和垂直电导率相对摄动量的关系
(A3)
其中,右端被积函数中的Sxz,H和Sxz,V分别称为横向感应电动势的空间灵敏度函数(或三维几何因子)并具有表达式
(A4)
附录B
补偿长源距幅度比和相位差的总径向微分几何因子:
补偿短源距幅度比和相位差的总径向微分几何因子:
补偿长源距幅度比和相位差的总纵向微分几何因子:
(B3)
补偿短源距幅度比和相位差的总纵向微分几何因子:
(B4)
幅度比和相位差的总空间灵敏度函数(或三维几何因子):
(B5)
补偿长源距幅度比和相位差的总空间灵敏度函数(或三维几何因子):
(B6)
补偿短源距幅度比和相位差的总空间灵敏度函数(或三维几何因子):
(B7)
补偿长源距幅度比和相位差对水平(垂直)电导率的径向微分几何因子:
(B8)
补偿短源距幅度比和相位差对水平(垂直)电导率的径向微分几何因子:
(B9)
补偿长源距幅度比和相位差对水平(垂直)电导率的纵向微分几何因子:
(B10)
补偿短源距幅度比和相位差对水平(垂直)电导率的纵向微分几何因子:
(B11)
交叉分量Vx1和Vx2的总空间灵敏度函数(或三维几何因子):
(B12)
补偿交叉分量的总空间灵敏度函数(或三维几何因子):
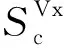
(B13)
