连续缺失地震数据的高阶流式预测滤波插值方法

吴庚， 刘财， 刘殿秘， 刘洋*， 郑植升

1 吉林大学地球探测科学与技术学院， 长春 130026 2 中国石油吉林油田勘探开发研究院， 松原 138003

0 引言

在地震勘探中，采集地震数据的数量和质量是获得高精度地下参数反演和解释的基础.地震数据在时间方向上总是充分采样的，而由于野外采集的经费限制以及环境因素的影响，如陆上勘探地表障碍物的存在以及海上勘探采集时电缆的羽漂等情况，实际数据在空间方向上是非规则分布且稀疏的.通过对地震数据进行插值重建，可以使其包含的信息更加充分地反映地下地质体的地球物理特征，提高对复杂地质构造和储层进行精细刻画的能力，因此往往需要在地震处理流程的早期阶段对采集到的数据进行插值或规则化处理.

缺失地震数据插值方法按照地震数据的缺失类型不同可以分为三类：随机缺失插值方法、规则缺失插值方法和连续缺失插值方法.由于地理环境因素的影响以及缺道坏道现象的存在，地震数据总是存在着随机缺失的问题.Curry(2003)提出了非平稳多尺度预测误差滤波器(PEF)对随机缺失数据进行插值.Herrmann等(2008)提出了curvelet变换方法对随机缺失地震数据进行重组.刘洋等(2018)提出了Bregman整形迭代插值方法，该方法能够利用有效的稀疏变换表征地震波场，迭代求解约束优化问题，对随机缺失地震道进行重建.Liu等(2019)提出了三维t-x-y域多尺度多方向自适应PEF对随机缺失数据进行插值.陈思远等(2021)提出了基于频率-结构双重加权阈值的随机缺失地震数据插值方法，保证了高低频信息的有效恢复.李昂等(2021)在OVT(Offset Vector Tile)域使用匹配追踪算法对五维地震数据进行插值.贺月等(2021)提出一种与字典学习相结合的凸集投影算法对地震数据插值的同时去噪.董烈乾等(2022)基于信噪比质控因子提出了优化迭代反演非规则数据重构方法，对三维随机缺失数据进行恢复.

基于成本考虑，地震数据在道间距或炮间距方向往往采样不足，可以通过规则地震数据缺失插值方法进行处理.Spitz(1991)提出了频率域预测滤波器(PF)，并用于地震道间插值.Porsani(1999)通过引入半步PF改进了Spitz的方法，实现更加有效的地震道加密.Wang(2002)进一步将预测插值从f-x域扩展到了f-x-y域，并对三维地震数据进行道间插值.Claerbout(1992)首次在地震道间插值中使用t-x域PEF.Crawley等(1999)设计了一种平滑变化的PEFs，通过“阶梯滤波器”控制滤波器的平滑来重建地震道间数据.Liu和Fomel(2011)提出t-x域正则化非平稳自回归(RNA)方法对规则和不规则缺失的地震数据进行插值，其方法主要使用整形正则化来控制自适应PEF的平滑性.Jia和Ma(2017)首次把机器学习应用到地震数据道间插值中，一定程度上克服了传统方法的物理假设条件.Wang等(2019)使用8层残差神经网络对规则缺失地震数据进行插值.Shao等(2021)使用Radon域地震干涉插值方法对规则数据进行重建.Shao和Wang(2022)使用稀疏Radon变换和动态标记函数对地震数据进行加密.

野外观测系统布置时，可能会遇到无法布置炮点或者无法埋置检波器的地段，如湖泊、工矿场和城镇等.这种情况下，观测系统中的测线连续性会受到影响，造成地震反射剖面间断现象，形成连续缺失，尽管实际施工中地震数据采集的变观方法能够一定程度解决这种问题，但是往往增加施工的复杂性.另外，由于在野外实际施工时，炮点位置附近无法布置检波器，总是会造成近炮检距缺失现象，这种情况在海上数据中尤为严重，影响后续的数据处理流程.因此，提出有效的连续缺失数据插值方法具有重要的实际意义.Trad等(2002)使用高分辨率时变Radon变换对近炮检距缺失数据进行重建.Naghizadeh和Sacchi(2007)提出了多步自回归地震数据插值方法，对规则、不规则和连续缺失数据进行重建.Van Groenestijn和Verschuur(2009)提出了稀疏反演一次波估计方法，并应用于地震近炮检距缺失数据上，克服了近偏移距数据缺失的影响.Wang等(2009)使用干涉插值方法对近炮检距缺失数据进行重建.Curry和Shan(2010)使用多重频率域PEFs对近炮检距缺失数据进行插值.Baumstein和Neelamani(2010)采用统计学和物理意义相结合的限定条件，将多种类型的先验信息和描述不同类型数据之间映射的方法相结合对连续缺失数据进行插值.Wang等(2010)提出了以模型为基础的干涉插值方法，对近炮检距缺失数据进行重建.Naghizadeh和Sacchi(2010)通过定义峰值的位置估计数据的空间谱，并使用自回归方法对规则和连续缺失数据进行插值.Naghizadeh(2012)通过定义稀疏分布的主倾角在频率波数域对连续缺失数据进行插值.Zu等(2016)使用倾斜条件限定地震数据插值反问题的病态方程，对连续缺失数据进行重建.Wang等(2022)基于深度学习方法对规则炮缺失数据和近偏移距缺失数据进行高精度重建.

以往的方法虽然在缺失地震道插值中有着较好的插值精度，但往往需要迭代计算，会导致增加内存占用和计算时间.为了解决这个问题，在Fomel和Claerbout(2016)提出的非迭代流式预测误差滤波器(SPEF)的基础上，Liu等(2022)和Zheng等(2022)分别在时间域和频率域提出流式预测滤波(SPF)方法进行地震道的插值重建.但这两种方法在大空缺地震道位置存在着滤波器系数无法更新的情况，难以处理连续缺失的地震数据插值问题.基于以上问题，本文提出了时间域非迭代的高阶流式预测滤波(HOSPF)方法对连续缺失地震数据进行插值，提出的高阶限定条件能够增加局部平滑性，改善以往SPF和SPEF在插值过程中滤波器难以更新的情况，从而提高连续缺失地震数据的插值精度.同时设计了与时间域高阶SPF相匹配的空间非因果预测滤波器和蛇形插值路径来减小插值误差.通过对比工业主流的傅里叶凸集投影(POCS)迭代插值方法，理论模型和实际数据测试结果表明，本文提出的方法能够在节省计算资源的同时保证连续缺失地震数据具有更高的插值精度，更加适合“两宽一高”地震勘探技术的需求.

1 基本理论

预测滤波是地震数据处理的重要理论之一，可以有效解决地震数据去噪和插值问题，其具体形式包含预测误差滤波器(PEF)和预测滤波器(PF)，PEF和相应的PF具有不同的滤波器结构和系数，PEF涉及到预测数据点时间方向上的因果预测系数，而PF只有空间方向的滤波器系数，同时，PEF的预测结果是残差，而PF的预测结果是数据本身.由于地震数据缺失是整道缺失，缺失数据在其对应的时间方向上没有预测关系，因此选用仅表征空间预测能力的PF在地震数据插值和抗噪声干扰能力上会优于PEF，因此本文选择PF进行地震数据插值.Claerbout(1992)提出PF对缺失数据进行插值的两个步骤.第一步从采集到的已知数据计算滤波器系数，第二步用计算的滤波器系数进行缺失数据插值.大多数的自适应PF都需要迭代计算来处理时空变化的地震同相轴信息，但是迭代方法增加了计算成本和存储量，因此本文提出一种扩展的非迭代时间域自适应PF插值方法.

1.1 高阶流式预测滤波系数解析估计

在二维情况下，自适应PF能够表示为：

(1)

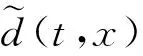
滤波器系数可以通过求解如下最小二乘问题得到：

(2)

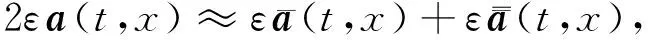
(3)

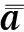
(4)

其中，εt和εx分别是沿着时间和空间方向的标量正则化参数.

公式(4)对应的最小二乘解形式为：

a(t,x)=[d(t,x)d(t,x)T+4ε2I]-1[d(t,x)d(t,x)

(5)

其中：

(6)

(7)

I表示单位矩阵.

公式(5)中逆矩阵可以通过迭代方法进行求解，比如共轭梯度法等，但迭代方法会增加计算成本和内存占用.由于该矩阵具有特殊的结构，本文使用Sherman-Morrison方法(Hager，1989)直接求解形如(L-MN)-1矩阵的逆，其中矩阵M和N分别代表了列向量和行向量.该矩阵的逆可以表示为：

(L-MN)-1=L-1+L-1M(I-NL-1M)-1NL-1,

(8)

其中，L和I-NL-1M是可逆的.在本文中，上述公式中L、M和N分别代表了4ε2I，-d(t,x)和d(t,x)T.因此，公式(5)可以写成解析解的形式：

(9)

由于公式(9)中当前系数a(t,x)依赖于处理路径中前面相邻的滤波器系数和数据值，因此在缺失数据中仅需要保证初始位置具有数据即可持续更新滤波器的时空变系数，初始的滤波器一般赋值为零，对于单边接收的近炮检距缺失数据，可以使用数据空间方向镜像的方式进行处理，从而保证HOSPF系数初始化的准确性.由于使用了更多时间和空间方向的已知滤波器进行约束，高阶流式预测滤波器能够更好地估计连续缺失地震数据位置的滤波器系数.

预测滤波器具有空间因果和空间非因果两种结构，空间非因果的PF使用了更多目标点附近的数据，这会比空间因果的滤波器有着更精准的插值结果.因此，本文选用空间非因果流式滤波器，以20个滤波器系数的空间非因果PF为例，其中滤波器大小为5(时间)×4(空间)，表达式为：

(10)

其中，·表示零值.

本文方法可以直接扩展为三维结构，相比于上述二维情况，仅需要额外增加一个空间方向上的约束.在三维情况下，增加沿着第二个空间轴y方向上的约束条件，因此三维情况下公式(4)可以写成：

(11)

公式(11)的最小二乘解为：

(12)

其中：

(13)

(14)

对比二维公式(6)，可以发现仅仅增加了一个y轴方向上的滤波器系数和标量正则化项.

正则化参数εt、εx和εy一般选取在待插值数据的最大值和最小值之间，并根据不同方向平滑程度的不同对三个正则化参数进行不同的调整.因此为了方便参数的设置，在进行插值之前，可以先对数据进行归一化处理.

1.2 非迭代缺失地震数据快速重建

在流式预测滤波器估计的同时，可以利用计算好的滤波器系数直接对缺失的地震道进行插值重建.以二维情况为例，对于HOSPF的残差r(t,x)，可以表示为：

r(t,x)=d(t,x)-d(t,x)Ta(t,x)

(15)

通过对公式(15)进行简单的数学变换，可以得到：

(16)

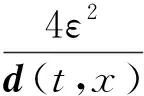
(17)

当使用估计出的HOSPF系数对缺失数据进行插值时，r(t,x)取0，则公式(17)进一步简化为：

(18)

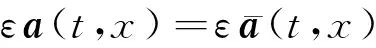
由于r(t,x)取0，公式(16)可简写为：

(19)

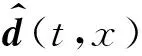
本文方法需要人为输入的参数有滤波器大小和标量正则化参数εn.通常根据地震同相轴的倾斜程度选择滤波器大小.εn的选取范围一般在输入数据最大值和最小值之间，为了方便参数的选取，可以对数据振幅进行归一化处理.

为了进一步提升插值精度，参考Zheng等(2022)的思路，针对HOSPF设计相匹配的时间-空间域插值路径.以二维情况为例，插值路径通常为图1a所示的沿着空间方向逐行进行插值，但这会导致每一行开始时，滤波器系数需要重新进行初始化计算，使得滤波器无法在整个数据中连续更新.针对这种情况，在二维时间-空间域内设计如图1b所示的蛇形插值路径.在逐行插值的基础上，相邻行采用空间反方向对数据进行滤波器系数计算和缺失数据重建，从而使得滤波器系数不需要对每行数据进行初始化操作，进一步提高HOSPF在数据边缘位置的插值精度.与Zheng等(2022)方法不同，本文的滤波器是在时间-空间平面沿着蛇形插值路径进行移动，当一个时空平面计算完后，移动到下一个时空平面上，而非在空间x-y平面沿着蛇形路径移动.

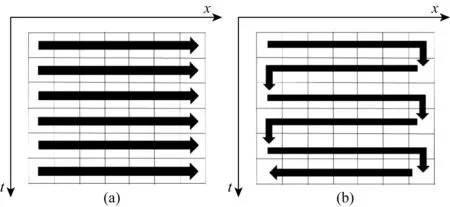
图1 不同模式的插值路径(a) 逐行插值路径； (b) 蛇形插值路径.Fig.1 Different strategies for interpolation path(a) The row-by-row interpolation path；(b) The snaky interpolation path.

2 理论模型测试

2.1 二维理论模型测试

本文将提出的HOSPF插值方法与工业常用的傅里叶凸集投影(POCS)(Abma and Kabir，2006)方法进行对比.为了定量地评价理论模型插值结果的精度，本文选取全局信噪比作为衡量标准(刘洋等，2017)：

(20)

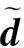
首先建立如图2a所示的理论模型，原始完整采样的数据包含了多条双曲同相轴，并且同相轴的振幅具有时空变化特征.首先随机移除40%地震道，并在此基础上，为了重点测试本文方法在连续缺失数据上的处理效果，又在第100道位置的附近连续移除了25道数据，其信噪比为2.72 dB.图3分别展示了二维傅里叶POCS、低阶流式预测滤波和本文提出的HOSPF方法的重建结果和插值误差，为了保证处理效果，傅里叶POCS方法中使用了6×3个重叠窗，每个重叠窗大小为150(时间方向)×150(空间方向)，经过测试迭代次数为575次可以获得收敛的插值结果，如图3a所示.傅里叶POCS方法能够比较有效地恢复随机缺失位置的地震道，同相轴的连续性得到提升，但是在连续缺失位置上效果并不理想，产生了较大的插值误差(图3b).低阶流式预测滤波器方法同样无法处理大面积连续缺失数据，同时在随机缺失数据位置也产生了一些空间假频.本文提出的HOSPF的参数中εt和εx均为0.5，滤波器大小为7(时间方向)×45(空间方向)，从插值结果(图3c)和插值误差(图3d)可以看到，本文提出的方法在连续缺失数据上有着更合理的插值精度，只是在同相轴倾角比较大的位置准确性有所降低，可以通过进一步提高滤波器的阶数来改善处理效果，但是同时也会使计算效率有所降低.傅里叶POCS、低阶流式预测滤波器和本文方法插值结果的信噪比分别为11.25 dB、10.38 dB和18.61 dB，同时这三种方法在使用相同单核CPU的计算时间分别为23.65 s、1.93 s和2.30 s，可见在保持合理插值结果的同时，本文提出的方法比傅里叶POCS具有更快的计算速度，同时，相比于低阶算法并没有增加太多的计算时间.

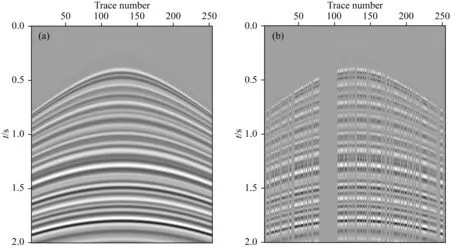
图2 二维理论模型测试(a) 原始完整采样数据； (b) 包含40%随机缺失和连续缺失的数据.Fig.2 2D synthetic data test(a) Original well-sampled data； (b) Data with 40% randomly removed and continuously missing traces.

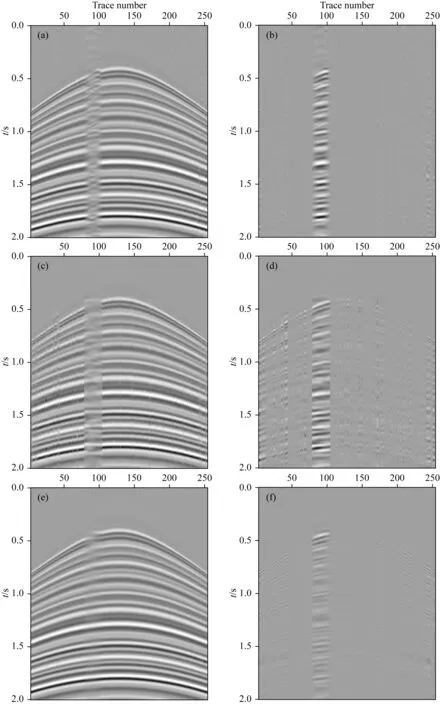
图3 二维模型不同方法的插值结果和误差(a)和(b) 傅里叶POCS插值结果和误差； (c)和(d) 低阶流式预测滤波插值结果和误差；(e)和(f) 本文提出HOSPF方法插值结果和误差.Fig.3 Interpolation results and errors of different methods for 2D synthetic model(a) and (b) Interpolated result and error by using Fourier POCS method； (c) and (d) Interpolation result and error by using low-order streaming prediction filter； (e) and (f) Interpolated result and error by using the proposed HOSPF.

2.2 三维理论模型测试

为了进一步测试提出方法在三维数据上处理的效果，选择有多个弯曲反射界面和一个断层的三维Qdome模型，如图4a所示.图4b展示了在随机去除70%地震道的同时移除空间范围35道×35道的方形区域，模拟连续缺失模型数据，相应的数据信噪比为1.40 dB.选用三维傅里叶POCS和低阶流式预测滤波器与本文提出的三维HOSPF插值方法进行对比.由于该模型数据中同相轴具有较小的斜率，因此未使用分窗处理，当迭代次数为84次，算法达到收敛.与二维模型处理结果类似，三维傅里叶POCS方法能够较好地重建非连续缺失的随机地震道，在近似线性同相轴的位置处具有较高的精度(图5a)，但是对于连续缺失的位置和断层及附近的同相轴则产生较大的插值误差，如图5b所示.低阶流式预测滤波器同样无法对连续缺失的地震道进行有效地插值，并在随机缺失的部分也产生了较大的误差，如图5c、d所示.选用本文提出的三维HOSPF进行数据的插值重建，滤波器参数包括：εt为0.00005，εx为0.0008，εy为0.00001，滤波器大小为7(时间方向)×5(空间X方向)×5(空间Y方向)，正则化参数的数值较小的原因在于该数据振幅值较小.从图5e所示的插值结果可以看到，本文提出的方法在三维情况下仍然能对大面积连续缺失地震道进行有效地恢复，除了断层位置和连续缺失的地震道相比较随机地震道位置的插值精度有一定程度的降低外，总体具有更合理的插值效果.傅里叶POCS、低阶算法和本文方法的处理结果信噪比分别提升至13.77 dB、12.61 dB和16.12 dB，三维傅里叶POCS方法在该模型上收敛的比较快，在使用相同单核CPU的计算时间为48.01 s，而低阶和高阶流式预测滤波器方法的计算时间分别为21.68 s和23.48 s.

图4 三维理论模型测试(a) 三维理论数据； (b) 随机缺失70%地震道和空间连续缺失数据.Fig.4 3D synthetic modeling test(a) 3D synthetic data； (b) The data with 70% randomly removed traces and a large continuous gap.

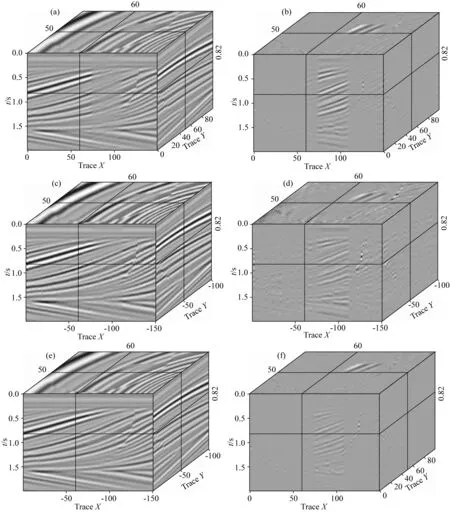
图5 三维模型不同方法的插值结果和误差(a)和(b) 傅里叶POCS插值结果和误差； (c)和(d) 低阶流式预测滤波插值结果和误差； (e)和(f) 本文提出HOSPF方法插值结果和误差.Fig.5 Interpolation results and errors of different methods for 3D synthetic model(a) and (b) Interpolated result and error by using Fourier POCS method； (c) and (d) Interpolation result and error by using low-order streaming prediction filter； (e) and (f) Interpolated result and error by using the proposed HOSPF.

3 实际数据测试

为了验证本文方法在实际数据处理中的适应性，选用墨西哥湾海上三维地震数据(Claerbout，2008)进行测试.原始数据如图6a所示，拖缆采集的实施方式造成数据近炮检距缺失.首先对数据进行了40%随机地震道的去除，并且在共中心点方向模拟30个共中心点道集的连续缺失(图6b).同样选用三维傅里叶POCS、低阶流式预测滤波器与本文提出的三维HOSPF插值方法作为对比，图7展示了三种方法的处理效果.三维傅里叶POCS在74次迭代时达到收敛标准，能够有效重建随机缺失和小范围连续缺失的近炮检距缺失道，但是对于大范围连续缺失的地震道则无法有效进行插值，说明该方法的处理能力受限于连续缺失的地震道数量(图7a).低阶流式预测滤波器在处理连续缺失和近炮检距数据效果同样不理想，无法有效恢复同相轴的能量(图7b).接下来，选取三维HOSPF的滤波器参数，根据数据的振幅和时空方向的数据平滑性，设置εt和εy均为0.5，εx为0.01，滤波器大小为15(时间方向)×40(共中心点方向)×5(炮检距方向)，本文提出的三维HOSPF相较于傅里叶POCS和传统流式预测滤波器插值方法有更好的插值精度，不仅在大范围连续缺失的位置明显改善插值效果，对于近炮检距和随机缺失道的重建效果也更加合理，插值后数据与相邻的已知数据之间能量更加接近(图7c).图8和图9分别为实际数据炮检距为0.1675 km位置的共炮检距剖面插值结果和误差的局部放大图，二者使用了相同的显示参数，可以看出在连续缺失和随机缺失位置上，本文提出的方法相较于其他两种方法插值效果更好，同相轴更加连续，同时计算速度更快，三维傅里叶POCS方法、低阶流式预测滤波器和本文提出HOSPF方法在使用相同单核CPU的计算时间分别为：98.75 s、48.46 s和53.70 s.

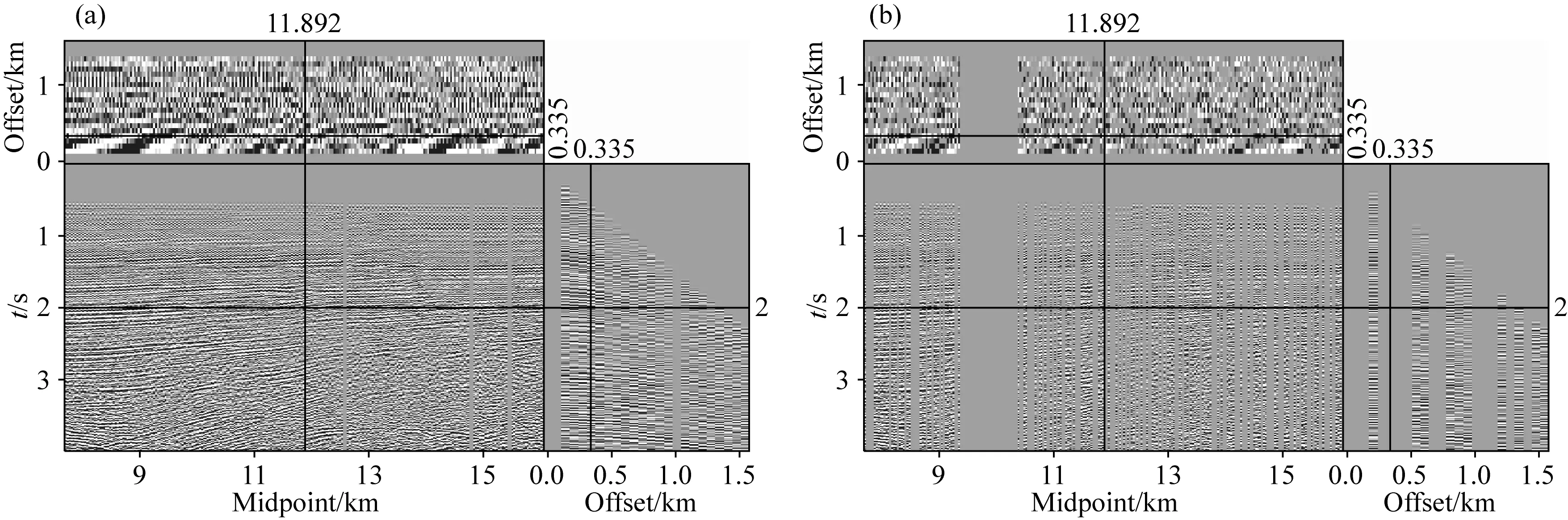
图6 实际模型测试(a) 有近炮检距缺失的三维实际数据； (b) 包含40%随机缺失和30个CMP连续缺失的数据.Fig.6 The field modeling test(a) 3D field data with near-offset missing data； (b) Data with 40% randomly removed and 30 continuously missing CMPs.

图8 实际数据插值结果局部放大比较(a) 三维傅里叶POCS方法； (b) 低阶流式预测滤波方法； (c) 本文提出的三维HOSPF方法.Fig.8 Close-up comparison of field data interpolation results(a) 3D Fourier POCS； (b) Low-order streaming prediction filter; (c) The proposed 3D HOSPF.

图9 实际数据误差局部放大比较(a) 三维傅里叶POCS方法； (b) 低阶流式预测滤波方法； (c) 本文提出的三维HOSPF方法.Fig.9 Close-up comparison of field data errors(a) 3D Fourier POCS； (b) Low-order streaming prediction filter; (c) The proposed 3D HOSPF.

4 结论与展望

本文提出了一种非迭代的时间域高阶流式预测滤波(HOSPF)插值方法.通过高阶约束条件进一步强化局部平滑性在缺失数据插值中的适用性，改善传统SPF方法在处理连续缺失数据插值问题中滤波器难以连续更新的问题，本文提出的方法能够有效处理大范围连续缺失数据的插值重建问题，提供更合理的插值精度.由于本方法不需要进行迭代，所以有高效的计算速度和较低的计算成本.同时，针对HOSPF的处理特点，选用空间非因果滤波器并设计了新的时间-空间域蛇形插值路径，进一步提高插值精度并改善边界效应.对理论模型和实际数据进行处理和分析，并对比工业主流傅里叶POCS方法，本文提出的方法在提供更加合理的连续缺失数据插值精度的前提下，占用更少的计算资源，尤其适用于高维地震数据的插值重建问题.

致谢感谢同济大学王本锋研究员的建议和帮助，感谢两位匿名审稿专家提出的宝贵意见.